الگوریتم DBSCAN در پایتون – راهنمای کاربردی

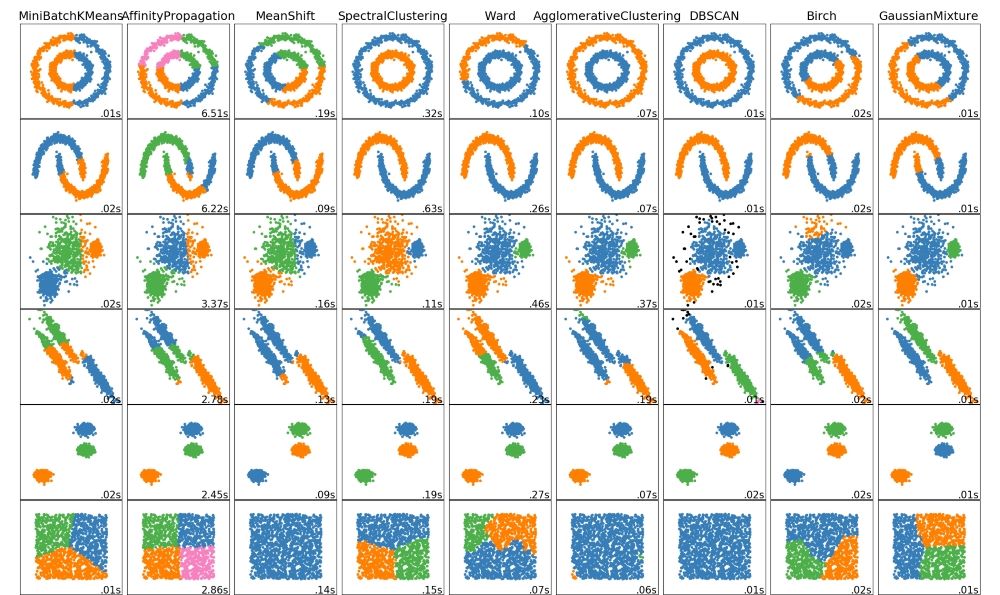
الگوریتم‌های «یادگیری ماشین» (Machine Learning)، در سه دسته «نظارت شده» (Supervised)، «نظارت نشده» (Unsupervised) و «یادگیری تقویتی» (Reinforcement Learning) قرار دارند. این الگوریتم‌ها، به ویژه دو دسته اول، در «داده‌کاوی» (Data Mining) و «علم داده» (Data Science) مورد استفاده قرار می‌گیرند. یکی از الگوریتم‌های نظارت نشده‌ای که برای کار «خوشه‌بندی» (Clustering) از آن استفاده می‌شود، الگوریتم DBSCAN است. در این مطلب، الگوریتم DBSCAN با یک مثال تشریح و پیاده‌سازی آن با «زبان برنامه‌نویسی پایتون» (Python Programming Language) انجام شده است.

خوشه‌بندی

«خوشه‌بندی» (Clustering)، کار بخش‌بندی داده‌ها در گروه‌هایی است که به آن‌ها «خوشه» (Cluster) گفته می‌شود. هدف از خوشه‌بندی، تقسیم کردن داده‌ها به صورتی است که در یک خوشه حداکثر مشابهت میان نقاط داده و بین داده‌ها در خوشه‌های گوناگون، کمترین مشابهت وجود داشته باشد. به عبارت دیگر، هدف از خوشه‌بندی قرار دادن نقاط داده در خوشه‌هایی با حداکثر مشابهت درون خوشه‌ای و حداقل مشابهت میان خوشه‌ای است. در ادامه، ابتدا الگوریتم خوشه‌بندی K-Means روی یک مجموعه داده اعمال و سپس الگوریتم DBSCAN روی آن اعمال می‌شود. سپس، خروجی‌های هر دو الگوریتم مورد بررسی قرار می‌گیرند و با یکدیگر مقایسه می‌شوند.

خوشه‌بندی k-means

در خوشه‌بندی K-Means یا K-میانگین، تلاش می‌شود تا مراکز دسته‌ای یافت شوند که نماینده ناحیه خاصی از داده‌ها هستند. در این الگوریتم، هر نقطه داده به نزدیک‌ترین مرکز خوشه نسبت به خودش، تخصیص داده می‌شود. سپس، مرکز خوشه‌ها بر اساس میانگین نقاط داده‌ای که به آن خوشه تخصیص داده شده‌اند مجددا محاسبه و تعیین می‌شوند.

فیلم آموزش خوشه بندی K میانگین K-Means با اس پی اس اس SPSS در فرادرس

کلیک کنید

این الگوریتم هنگامی پایان می‌یابد که تخصیص نمونه‌ها به خوشه‌ها دیگر تغییر نکند. ارائه بصری از الگوریتم خوشه‌بندی K-Means به صورت زیر خواهد بود.

1import mglearn
2mglearn.plots.plot_kmeans_algorithm()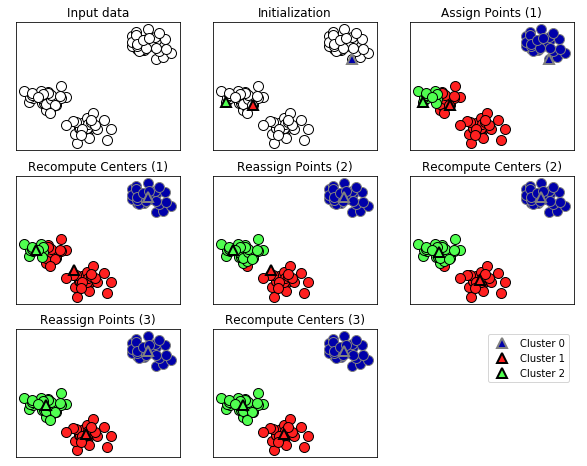

یک مشکل الگوریتم خوشه‌بندی K-Means آن است که این الگوریتم فرض می‌کند همه جهت‌ها برای هر خوشه به طور مساوی با هم حائز اهمیت هستند. وجود چنین رویکردی معمولا مشکل بزرگی نیست، مگر اینکه شکل داده‌های موجود عجیب باشد. در واقع، نقاط داده اشکال S مانند یا دیگر انواع شکل‌ها را داشته باشند.

در این مطلب، چنین نوع داده‌هایی به طور مصنوعی ساخته شده است. با بهره‌گیری از کد زیر که از کتاب «مقدمه‌ای بر یادگیری ماشین با پایتون» (Introduction to Machine Learning with Python) اثر «آندرس مولر» (Andreas C. Müller) و «سارا گیدو» (Sarah Guido) برداشته شده است (با تغییرات جزئی در تعداد خوشه‌ها)، می‌توان داده‌هایی تولید کرد که الگوریتم K-Means قادر به مدیریت کردن آن‌ها به درستی نیست.

1import numpy as np
2import matplotlib.pyplot as plt
3from sklearn.datasets import make_blobs
4from sklearn.cluster import KMeans
5# generate some random cluster data
6X, y = make_blobs(random_state=170, n_samples=600, centers = 5)
7rng = np.random.RandomState(74)
8# transform the data to be stretched
9transformation = rng.normal(size=(2, 2))
10X = np.dot(X, transformation)
11# plot
12plt.scatter(X[:, 0], X[:, 1])
13plt.xlabel("Feature 0")
14plt.ylabel("Feature 1")
15plt.show()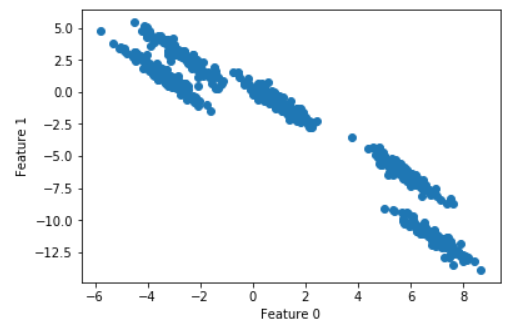

همانطور که مشهود است، در داده‌های تولید شده به وسیله یک کد، پنج خوشه با شکل قطری کشیده وجود دارد. در ادامه، الگوریتم خوشه‌بندی K-Means روی این داده‌ها اعمال می‌شود.

1# cluster the data into five clusters
2kmeans = KMeans(n_clusters=5)
3kmeans.fit(X)
4y_pred = kmeans.predict(X)
5# plot the cluster assignments and cluster centers
6plt.scatter(X[:, 0], X[:, 1], c=y_pred, cmap="plasma")
7plt.scatter(kmeans.cluster_centers_[:, 0],   
8            kmeans.cluster_centers_[:, 1],
9            marker='^', 
10            c=[0, 1, 2, 3, 4], 
11            s=100, 
12            linewidth=2,
13            cmap="plasma")
14plt.xlabel("Feature 0")
15plt.ylabel("Feature 1")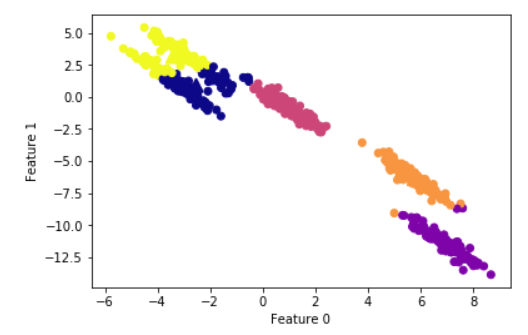

می‌توان مشاهده کرد که الگوریتم K-Means قادر است به درستی خوشه‌ها را در وسط و پایین شناسایی کند، در حالیکه در خوشه‌های بالایی که بسیار نزدیک به هم هستند دچار اشکال شده است. این خوشه‌ها به سمت قطر کشیده شده‌اند. از آنجا که الگوریتم K-Means صرفا فاصله تا نزدیک‌ترین مرکز خوشه را در نظر می‌گیرد، نمی‌تواند این نوع از داده‌ها را مدیریت کند. در ادامه، از الگوریتم DBSCAN برای حل چنین مسائلی استفاده خواهد شد.

الگوریتم DBSCAN

نام کامل این الگوریتم، «خوشه‌بندی فضایی مبتنی بر چگالی در کاربردهای دارای نویز» (Density Based Spatial Clustering of Applications with Noise) است که به اختصار به آن DBSCAN گفته می‌شود. در الگوریتم DBSCAN نیازی به این نیست که تعداد خوشه‌ها از ابتدا تعیین شود. این الگوریتم می‌تواند خوشه‌های دارای اشکال پیچیده را کشف کند. همچنین، می‌تواند نقاط داده‌ای که بخشی از هیچ خوشه‌ای نیستند (نقاط دورافتاده یا ناهنجار) را شناسایی کند.

این قابلیت برای تشخیص ناهنجاری بسیار مفید است. DBSCAN با شناسایی نقاطی که در نواحی شلوغ (چگال) از «فضای ویژگی» (Feature Space) قرار دارند کار می‌کند. منظور از نواحی چگال، قسمت‌هایی است که نقاط داده بسیار به یکدیگر نزدیک هستند (نواحی چگال در فضای ویژگی). برخی از نکات کلیدی پیرامون الگوریتم DBSCAN در ادامه آمده‌اند.

• دو پارامتر min_samples و eps در الگوریتم DBSCAN وجود دارد.
• هر نقطه داده، از دیگر نقاط داده فاصله‌ای دارد. هر نقطه‌ای که فاصله‌اش با یک نقطه مفروض کمتر از eps باشد، به عنوان همسایه آن نقطه در نظر گرفت می‌شود.
• هر نقطه داده مفروضی که min_samples همسایه داشته باشد، یک نقطه «مرکزی» (Core) محسوب می‌شود.
• «نمونه‌های مرکزی» (core samples) که نسبت به یکدیگر نزدیک‌تر از فاصله eps هستند، در خوشه مشابهی قرار می‌گیرند.

در ادامه، مثالی از انجام خوشه‌بندی، با انتخاب دو پارامتر eps و min_samples ارائه شده است.

1mglearn.plots.plot_dbscan()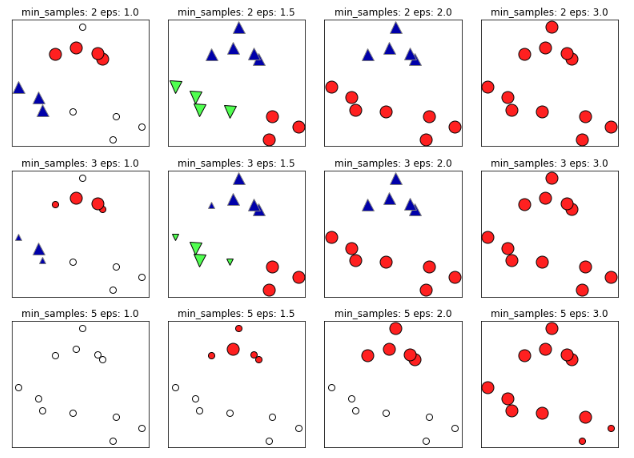

در نمودار بالا، نقاطی که به خوشه‌ها تخصیص داده شده‌اند سخت هستند. نقاط «نویز» (Noise) در تصویر به رنگ سفید و نمونه‌های مرکزی به صورت نشانگرهای بزرگی نمایش داده شده‌اند. این در حالی است که نقاط مرزی به صورت نشانگرهای کوچک‌تری نشان داده شده‌اند. افزایش eps (حرکت از چپ به راست در تصویر) بدین معنا است که نقاط بیشتری در خوشه‌ها قرار داده خواهند شد. این کار موجب می‌شود که خوشه‌ها رشد کنند، در عین حال ممکن است منجر به آن بشود که چندین خوشه به یک خوشه بپیوندند. افزایش min_samples (حرکت از بالا به پایین تصویر)، به معنای آن است که نقاط کمتری نقاط مرکزی خواهند بود و نقاط بیشتری به عنوان نویز در نظر گرفته خواهند شد.

پارامتر eps مهم‌تر است، زیرا مشخص می‌کند که برای نقاط، نزدیک بودن چه معنایی دارد. تنظیم eps روی یک مقدار خیلی کوچک بدان معنا است که هیچ نقطه‌ای، نقطه مرکزی نیست و امکان دارد منجر به آن شود که همه نقاط به عنوان نویز برچسب‌گذاری شوند. تنظیم eps روی یک مقدار خیلی بزرگ ممکن است منجر به آن شود که همه نقاط در یک خوشه قرار بگیرند. اکنون به مثال بازگشته و بررسی می‌شود که DBSCAN چگونه با داده‌های تولید شده در بالا که شکل خاصی داشتند مواجه خواهد شد.

1from sklearn.cluster import DBSCAN
2from sklearn.preprocessing import StandardScaler
3scaler = StandardScaler()
4X_scaled = scaler.fit_transform(X)
5# cluster the data into five clusters
6dbscan = DBSCAN(eps=0.123, min_samples = 2)
7clusters = dbscan.fit_predict(X_scaled)
8# plot the cluster assignments
9plt.scatter(X[:, 0], X[:, 1], c=clusters, cmap="plasma")
10plt.xlabel("Feature 0")
11plt.ylabel("Feature 1")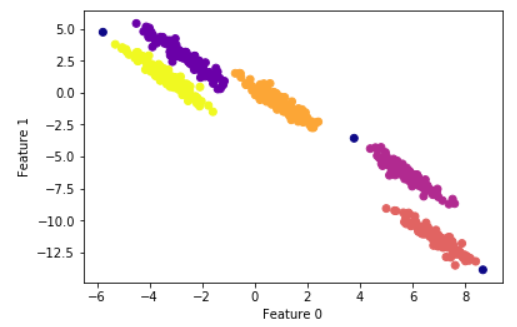

پس از پیچش eps و min_samples برای مدتی، خوشه‌های نسبتا سازگاری حاصل شد که هنوز هم شامل نقاط نویز هستند.

• در حالیکه DBSCAN نیازی به آن ندارد که تعداد خوشه‌ها صراحتا به آن داده شوند، تنظیم eps موجب می‌شود که به طور ضمنی تعداد خوشه‌هایی که باید پیدا شوند توسط الگوریتم کنترل شود.
• یافتن یک تنظیمات خوب برای eps گاهی پس از مقیاس دادن داده‌ها آسان‌تر است، زیرا استفاده از روش‌های مقیاس‌دهی این اطمینان را به وجود می‌آورد که همه ویژگی‌ها دارای طیف مشابهی هستند.

فیلم مجموعه آموزش داده کاوی و یادگیری ماشین – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

در نهایت، با در نظر داشتن این موضوع که داده‌ها به نوعی ساخته شده‌اند که پنج خوشه را صراحتا تعریف کنند، می‌توان کارایی را با استفاده از adjusted_rand_score اندازه‌گیری کرد. این کار در مسائل واقعی انجام‌پذیر نیست، زیرا در آن‌ها برچسب‌های خوشه برای آغاز کار موجود نیستند (اصلا به دلیل موجود نبودن داده‌های برچسب‌دار نیاز به اعمال روش‌های خوشه‌بندی به جای دسته‌بندی است). با توجه به اینکه در این مثال برچسب‌ها موجود هستند، می‌توان کارایی را اندازه‌گیری کرد.

1from sklearn.metrics.cluster import adjusted_rand_score
2#k-means performance:
3print("ARI =", adjusted_rand_score(y, y_pred).round(2))
4ARI = 0.76
5#DBSCAN performance:
6print("ARI =", adjusted_rand_score(y, clusters).round(2))
7ARI = 0.99

الگوریتم DBSCAN عالی عمل کرده است و توانسته امتیاز کارایی ۰.۹۹ را به دست آورد، در حالیکه K-Means امتیاز کارایی 0.76 دارد.

اگر نوشته بالا برای شما مفید بود، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش‌های داده‌کاوی یا Data Mining در متلب
• مجموعه آموزش‌های مدل سازی، برازش و تخمین
• داده‌کاوی (Data Mining) — از صفر تا صد
• یادگیری علم داده (Data Science) با پایتون — از صفر تا صد

^^