مبانی تحلیل تیرهای کامپوزیتی – با مثال های کاربردی

در مباحث «طراحی تیر در شرایط بارگذاری خمشی»، «تحلیل تیرهای غیر منشوری»، «تنش های نرمال موجود در تیرها» و دیگر مطالب مرتبط با تحلیل تیرها، به بررسی رفتار انواع مختلف تیر در شرایط بارگذاری متفاوت پرداختیم. در تمام مباحث مذکور، تیر مورد تحلیل تنها از یک ماده واحد ساخته شده بود. در این مقاله، شما را با مبانی تحلیل تنش‌های ناشی از اعمال بار بر روی تیرهای کامپوزیتی آشنا خواهیم کرد. در انتها نیز به منظور آشنایی بهتر با نحوه به کارگیری مفاهیم و روابط ارائه شده، به تشریح چند مثال کاربردی خواهیم پرداخت.

تیرهای کامپوزیتی

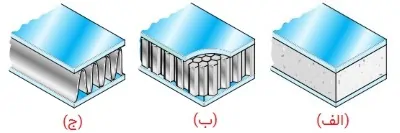
به تیرهایی که از دو یا چند ماده مختلف ساخته شده باشند، «تیرهای کامپوزیتی» (Composite Beams) گفته می‌شود. تیرهای «دوفلزی» (Bimetallical) مورد استفاده در ترموستات‌ها، لوله‌های دارای پوشش پلاستیکی، تیرهای چوبی دارای صفحات تقویت کننده فولادی، نمونه هایی از تیرهای کامپوزیتی هستند که تصویر آن‌ها در شکل زیر نمایش داده شده است.

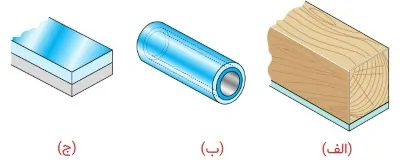
در سال‌های اخیر، انواع متعددی از تیرهای کامپوزیتی وارد صنعت شده‌اند. هدف اصلی از به کارگیری این تیرها، صرفه‌جویی در مواد مصرفی و کاهش وزن سازه‌ها است. «تیرهای ساندویچی» (Sandwich Beams) به عنوان یکی از انواع تیرهای کامپوزیتی، کاربرد وسیعی در صنایع هوایی و هوافضا دارند؛ چراکه در این صنایع، به کارگیری قطعات سبک با مقاومت و صلبیت بالا از اهمیت زیادی برخوردار است. وسایل شناخته شده مختلفی نظیر قفسه‌های کتاب، جعبه‌های مقوایی، درها و ... نیز به سبک تیرهای ساندویچی ساخته می‌شوند.

شکل زیر، نمونه‌هایی از تیرهای ساندویچی را نمایش می‌دهد. نمونه معمولی این تیر از دو صفحه نازک با مقاومت نسبتاً بالا (مانند صفحات آلومینیومی) و یک هسته ضخیم با وزن کم و مقاومت پایین (مانند پلاستیک) تشکیل می‌شود. به دلیل فاصله زیاد صفحات از محور خنثی (محل رخ دادن بیشترین تنش خمشی)، رفتار آنها مشابه بال های یک تیر I شکل است. هسته تیر ساندویچی همانند یک پرکننده عمل می‌کند و نگهداری لازم برای صفحات را فراهم می‌سازد (این پیکربندی باعث جلوگیری از کمانش و چین‌خوردگی صفحات می‌شود). پلاستیک و فوم‌های سبک اغلب برای هسته تیرهای کامپوزیتی مورد استفاده قرار می‌گیرند. در بخش بعدی، به معرفی نحوه تحلیل تیرهای کامپوزیتی می‌پردازیم.

تنش و کرنش موجود در تیرهای کامپوزیتی

با استفاده از اصول اولیه محاسبه کرنش‌های موجود در تیرهای متشکل از یک ماده می‌توان کرنش‌های موجود در تیرهای کامپوزیتی را نیز تعیین کرد (مخصوصاً اگر نقاط تشکیل دهنده مقاطع عرضی تیر در حین اعمال خمش بر روی صفحه قبلی خود باقی بمانند). این قاعده همیشه برای حالت خمش خالص صدق می‌کند و به ماهیت ماده تشکیل دهنده تیر بستگی ندارد. از این‌رو، در یک تیر کامپوزیتی میزان کرنش طولی ε_x با حرکت از سمت بالا تا پایین تیر به صورت خطی تغییر می‌کند. رابطه این کرنش عبارت است از:

y: فاصله نقطه مورد بررسی تا محور خنثی؛ ρ: شعاع انحنا؛ k: انحنا

برای محاسبه تنش و کرنش موجود در هر نوع تیر کامپوزیتی باید از رابطه بالا شروع کنیم. به منظور نمایش چگونگی اجرای این عملیات، تیر کامپوزیتی نمایش داده شده در شکل زیر را در نظر بگیرید. این تیر از دو ماده متفاوت (ماده 1 و 2) تشکیل شده است.

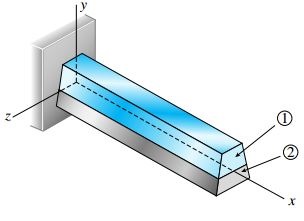
ترکیب دو ماده تشکیل دهنده تیر کامپوزیتی بالا به گونه‌ای است که می‌توان رفتار آن در برابر بارهای اعمال شده را مانند رفتار یک ماده واحد در نظر گرفت. در شکل بالا، صفحه x-y را به عنوان صفحه تقارن و صفحه x-z را به عنوان صفحه خنثی تیر در نظر می‌گیریم. البته توجه، به دلیل استفاده از دو ماده برای ساخت این تیر، محور خنثی (محور z در شکل زیر) از مرکز هندسی عبور نمی‌کند.

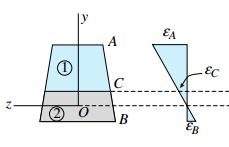
اگر تیر کامپوزیتی بالا با انحنای مثبت خم شود، کرنش‌های ε_x مانند شکل زیر تغییر می‌کنند. در این نمودار، کرنش فشاری موجود در بالای تیر با ε_A، کرنش کششی موجود در پایین تیر با ε_B و کرنش موجود در سطح اتصال دو ماده با ε_C نمایش داده شده است. به خاطر داشته باشید که هیچ کرنشی بر روی محور خنثی رخ نمی‌دهد.

تنش‌های نرمال اعمال شده بر روی سطح مقطع با استفاده از کرنش‌های موجود و روابط تنش-کرنش مواد تشکیل دهنده تیر به دست می‌آیند. با در نظر گرفتن رفتار الاستیک خطی برای مواد تشکیل دهنده تیر می‌توانیم از قانون هوک به منظور محاسبه تنش تک محوری کمک بگیریم. به این ترتیب، مقدار تنش‌های موجود در این مواد برابر حاصلضرب کرنش در مدول الاستیسیته خواهد بود.

در اینجا، مدول الاستیسیته ماده 1 و 2 را به ترتیب با حروف E₁ و E₂ نمایش می‌دهیم و فرض می‌کنیم که رابطه E₂>E₁ بین این دو مدول برقرار است. با در نظر گرفتن این نکات، یک نمودار توزیع تنش مطابق شکل زیر به دست می‌آید. تنش فشاری اعمال شده بر بخش بالایی تیر با استفاده از رابطه σ_A=E₁ε_A و تنش کششی موجود در بخش پایینی آن با استفاده از رابطه σ_B=E₂ε_B محاسبه می‌شود.

در سطح اتصال C، تنش‌های موجود در هر ماده با یکدیگر تفاوت دارند. دلیل این اختلاف، برابر نبودن مدول الاستیسیته مواد است. مقدار این تنش‌ها در ماده 1، از رابطه σ₁C=E₁ε_C و در ماده 2، از رابطه σ₂C=E₂ε_C به دست می‌آید. با کمک قانون هوک و رابطه کرنش طولی ε_x می‌توانیم تنش‌های نرمال موجود در فاصله y از محور خنثی را بر اساس مفهوم انحنا بیان کنیم:

σ_x1: تنش در ماده 1 و σ_x2: تنش در ماده 2

در مرحله بعد می‌توان با کمک معادلات بالا و تعیین محل قرارگیری محور خنثی، رابطه گشتاور-انحنا را به دست آورد. در بخش بعدی، به معرفی نحوه تعیین موقعیت محور خنثی می‌پردازیم.

محور خنثی

محل قرارگیری محور خنثی (محور z) با تعیین شرایطی به دست می‌آید که در آن، برآیند نیروی محوری موجود بر روی مقطع عرضی برابر با صفر باشد. به این ترتیب داریم:

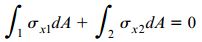
محدوده انتگرال اول بر روی سطح مقطع ماده 1 و محدوده انتگرال دو بر روی سطح مقطع ماده 2 قرار دارد. با جایگذاری روابط σ_x1 و σ_x2 در معادله بالا خواهیم داشت:

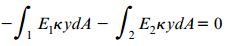
به دلیل ثابت بودن مقدار انحنا بر روی تمام مقاطع عرضی، می‌توانیم پارامتر k را از معادله بالا حذف کنیم. در این صورت، فرم ساده شده معادله تعیین موقعیت محور خنثی به شکل زیر تبدیل می‌شود:

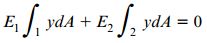
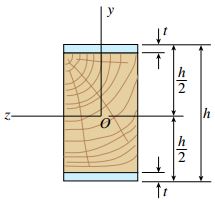
انتگرال‌های معادله بالا، گشتاورهای اول سطح 1 و 2 نسبت به محور خنثی را نمایش می‌دهند. معادله بالا، حالت کلی معادله معرفی شده برای یک تیر متشکل از یک ماده است (در مثال انتهای مقاله، به تشریح جزئیات فرآیند تعیین محل قرارگیری محور خنثی خواهیم پرداخت). اگر سطح مقطع تیر مانند شکل زیر دارای تقارن مضاعف باشد، محور خنثی در میانه سطح مقطع قرار خواهد داشت. در این حالت، به محاسبه محل قرارگیری این محور با استفاده از معادله معرفی شده نیازی نیست.

رابطه بین گشتاور و انحنا

رابطه بین گشتاور و انحنا در یک تیر کامپوزیتی متشکل از دو ماده را می‌توان با در نظر گرفتن یک حالت خاص تعیین کرد. در این حالت، برآیند گشتاور تنش‌های خمشی با گشتاور خمشی اعمال شده بر روی سطح مقطع برابر است. با استفاده از روابط معرفی شده برای σ_x1 و σ_x2 در این مقاله و مشابه روند ارائه شده برای تعیین رابطه گشتاور-انحنا در مبحث «تنش های نرمال موجود در تیرها»، داریم:

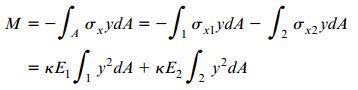
فرم ساده شده معادله بالا به صورت زیر است:

I₁ و I₂ به ترتیب ممان اینرسی حول محور خنثی (محور z) بر روی سطح مقطع مواد 1 و 2 را نمایش می‌دهند. توجه داشته باشید که از مجموع ممان اینرسی‌های بالا، ممان اینرسی بر روی تمام سطح مقطع تیر به دست می‌آید (I=I₁+I₂). اکنون می‌توانیم معادله بالا را برای محاسبه انحنا k بر حسب گشتاور خمشی M بازنویسی کنیم:

این معادله با عنوان «رابطه گشتاور-انحنا» (Moment-Curvature Relationship) برای یک تیر متشکل از دو ماده شناخته می‌شود. مخرج کسر در عبارت سمت راست این معادله، رابطه مورد استفاده تعیین «صلبیت پیچشی» (Flexural Rigidity) برای تیر کامپوزیتی است.

تنش‌های نرمال (رابطه پیچش)

مقدار تنش‌های نرمال موجود در تیر با جایگذاری رابطه انحنا در روابط σ_x1 و σ_x2 به دست می‌آید:

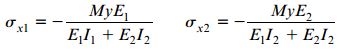
روابط بالا با عنوان «روابط پیچش تیر کامپوزیتی» شناخته می‌شوند. در صورت برابر بودن مدول الاستیسیته هر دو ماده (E₁=E₂=E)، هر دو رابطه بالا به رابطه پیچش تیر متشکل از یک ماده تبدیل خواهند شد. در مثال‌های انتهای این مقاله، تیرهای کامپوزیتی را با کمک روابط ارائه شده مورد تحلیل قرار خواهیم داد.

تخمین خمش برای تیرهای ساندویچی

تیر ساندویچی، سازه‌ای متشکل از دو ماده الاستیک خطی است که مقاطع عرضی آن دارای تقارن مضاعف هستند (شکل زیر). به منظور تحلیل این تیرها می‌توان از روابط ارائه شده در بخش‌های قبلی کمک گرفت. اگرچه، با استفاده از فرضیات ساده سازی مناسب، امکان تخمین میزان خمش در تیرهای ساندویچی فراهم می‌شود.

اگر مدول الاستیسیته ماده تشکیل دهنده صفحات بالایی و پایینی تیر (ماده 1) از مدول ماده تشکیل دهنده هسته آن (ماده 2) بزرگ‌تر باشد، نادیده گرفتن تنش‌های نرمال در هسته تیر و فرض مقاومت صفحات در برابر تمام تنش‌های خمشی طولی منطقی خواهد بود. در واقع بر اساس این فرضیات، مدول الاستیسیته هسته تیر (E₂) برابر با صفر در نظر گرفته می‌شود. با توجه به این شرایط، رابطه پیچش برای ماده 2، مقدار تنش نرمال σ_x2 نیز برابر صفر و رابطه پیچش برای ماده 1 به صورت زیر خواهد بود:

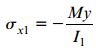
رابطه بالا مشابه رابطه پیچش برای تیر متشکل از یک ماده است. کمیت I₁، ممان اینرسی صفحات بالایی و پایینی نسبت به محور خنثی را نمایش می هد. بنابراین:

b: عرض تیر؛ h: طول کلی تیر؛ h_c=h-2t: طول هسته تیر؛ t: ضخامت صفحات

تنش‌های نرمال ماکسیمم در مقاطع بالایی و پایینی تیر ساندویچی (به ترتیب در موقعیت‌های y=h/2 و y=-h/2) رخ می‌دهند. بنابراین، با توجه به رابطه σ_x2 برای این نوع تیر خواهیم داشت:

اگر علامت گشتاور خمشی M مثبت باشد، سطح بالایی در معرض فشار و سطح پایینی تحت کشش قرار خواهد گرفت (به دلیل بزرگتر بودن تنش‌های به دست آمده از روابط بالا نسبت به تنش‌های حاصل از روابط پیچش، روش تخمینی معرفی شده در این مقاله به عنوان یک روش محافظه کارانه در نظر گرفته می‌شود). در صورت نازک بودن ضخامت صفحات نسبت به ضخامت هسته (کوچک‌تر بودن t از h_c)، نادیده گرفتن تنش‌های برشی موجود در صفحات و فرض مقاومت هسته در برابر تمام تنش‌های برشی منطقی خواهد بود. در این شرایط، روابط مورد نیاز برای تعیین تنش برشی میانگین و کرنش برشی میانگین عبارت‌اند از:

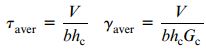
V: نیروی برشی اعمال شده بر روی سطح مقطع؛ G_c: مدول برشی ماده 2

با وجود بزرگتر بودن تنش برشی ماکسیمم و کرنش برشی ماکسیمم از مقادیر میانگین، در اغلب موارد از این مقادیر برای مقاصد طراحی استفاده می‌شود.

نکات تکمیلی

برای تحلیل تیرهای کامپوزیتی در این مقاله، فرض کردیم که مواد تشکیل دهنده تیر از قانون هوک پیروی می‌کنند. به علاوه، اتصال بین دو ماده را به اندازه‌ای قوی در نظر گرفتیم که رفتار آنها در برابر بارهای اعمال شده به صورت یک واحد یکپارچه باشد. از این‌رو، تحلیل‌های ارائه شده با فرض شرایط ایده آل و تنها برای درک ابتدایی نحوه رفتار تیرهای کامپوزیتی بود. تیرهای بتن مسلح، به عنوان یکی از پیچیده‌ترین انواع سازه‌های کامپوزیتی شناخته می‌شوند (شکل زیر). رفتار این تیرها تفاوت قابل توجهی با مطالب ارائه شده در این مقاله دارد. بتن در برابر اعمال فشار بسیار مقاوم ولی در برابر کشش بسیار ضعیف است. از این‌رو، معمولاً از در نظر گرفتن مقاومت کششی آن در محاسبات به طور کامل صرفنظر می‌شود. به این ترتیب، روابط معرفی شده در این مقاله برای تیرهای بتن مسلح قابل استفاده نخواهند بود.

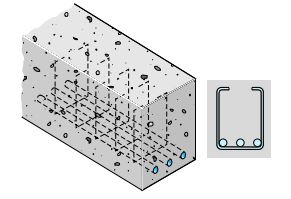
توجه داشته باشید که اکثر تیرهای بتن مسلح بر اساس مبانی رفتار الاستیک خطی مواد طراحی نمی‌شوند. بنابراین به جای به کارگیری تنش‌های مجاز در طراحی این نوع تیرها، روش‌های واقع گرایانه تری بر مبنای ظرفیت باربری مورد استفاده قرار می‌گیرد.

مثال‌های کاربردی

در این بخش، به منظور آشنایی بهتر با نحوه به کارگیری روابط ارائه شده برای تحلیل تیرهای کامپوزیتی، دو مثال کاربردی را تشریح خواهیم کرد.

مثال 1

شکل زیر، یک تیر کامپوزیتی متشکل از یک تیر چوبی با ابعاد 4.0in*6.0in و یک صفحه تقویت کننده فولادی با ابعاد 4.0in*0.5in را نمایش می‌دهد. این تیر کامپوزیتی در معرض یک گشتاور خمشی مثبت به اندازه M=60kip-in قرار دارد. توجه داشته باشید که بخش چوبی و فولاد به طور مناسب به یکدیگر متصل شده‌اند. با توجه به اطلاعات مسئله، مقدار حداکثر تنش‌های فشاری و کششی موجود در چوب (ماده 1) و تنش‌های کششی ماکسیمم و مینیمم موجود در فولاد (ماده 2) را به دست بیاورید (مدول الاستیسیته ماده 1 و 2 به ترتیب برابر E₁=1500ksi و E₂=30000ksi است).

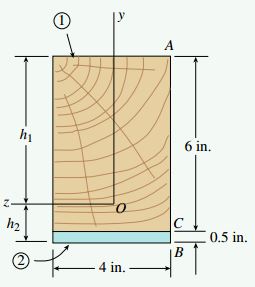
محور خنثی

اولین قدم در تحلیل این تیر، تعیین محل قرارگیری محور خنثی سطح مقطع آن است. به این منظور، فاصله محور خنثی تا بالا و پایین تیر را به ترتیب با حروف h₁ و h₂ نمایش می‌دهیم. برای محاسبه مقدار این فاصله‌ها، از رابطه معرفی شده در مقاله استفاده می‌کنیم. برای تعیین انتگرال‌های موجود در این رابطه (گشتاور اول سطح‌های 1 و 2 حول محور z) داریم:

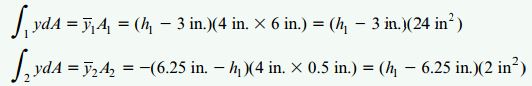
A₁: مساحت بخش چوبی؛ A₂: مساحت بخش فلزی؛ y^-₁: مختصات مرکز هندسی بخش چوبی؛ y^-₂: مختصات مرکز هندسی بخش فلزی؛ h₁: فاصله محور خنثی تا بالای تیر بر حسب واحد اینچ

با جایگذاری عبارت‌های بالا در رابطه محور خنثی، معادله تعیین محل قرارگیری این محور به دست می‌آید:

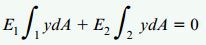
یا

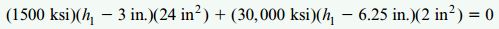
به منظور محاسبه فاصله محور خنثی تا سطح بالایی تیر، معادله بالا را بر حسب h₁ حل می‌کنیم:

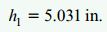
مقدار فاصله محور خنثی تا سطح پایینی تیر (h₂) نیز به صورت زیر خواهد بود:

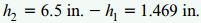
به این ترتیب، محل قرارگیری محور خنثی بر روی مقطع عرضی تیر به دست آمد.

ممان اینرسی سطح‌های 1 و 2

ممان اینرسی سطح‌های A₁ و A₂ نسبت به محور خنثی با استفاده از تئوری محور موازی محاسبه می‌شود. برای سطح مقطع ماده 1 داریم:

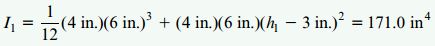
به همین ترتیب، برای سطح مقطع ماده 2 داریم:

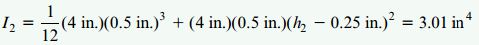
برای بررسی صحت محاسبات بالا، ممان اینرسی کل سطح مقطع تیر نسب به محور z را تعیین می‌کنیم:

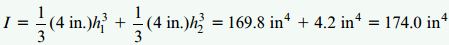
این مقدار با جمع I₁ و I₂ برابر است. به این ترتیب، صحت محاسبات تأیید می‌شود.

تنش‌های نرمال

تنش‌های موجود در مواد 1 و 2 از روابط پیچش برای تیرهای کامپوزیتی به دست می‌آیند. بیشترین تنش فشاری اعمال شده بر ماده 1 در بالای تیر (سطح A با مختصات y=h₁=5.031in) رخ می‌دهد. به این ترتیب:

بزرگ‌ترین تنش کششی اعمال شده بر ماده 1 در سطح اتصال دو ماده (سطح C با مختصات y=-(h₂-0.5in)=-0.969in) رخ می‌دهد. بنابراین:

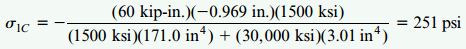
مقادیر به دست آمده، حداکثر تنش فشاری و کششی اعمال شده بر بخش چوبی تیر هستند. بخش فولادی تیر، پایین‌تر از محور خنثی قرار دارد. از این‌رو، تنها تنش‌های کششی به این بخش از تیر اعمال می‌شوند. تنش کششی ماکسیمم در پایین تیر (سطح B با مختصات y=-h₂=-1.469in) رخ می‌دهد. بنابراین:

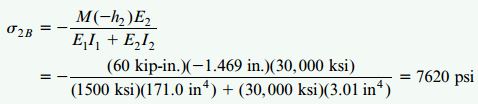
تنش کششی مینیمم در سطح اتصال دو ماده (سطح C با مختصات y=-0.969in) رخ می‌دهد. به این ترتیب:

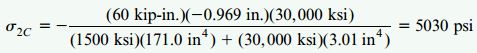
مقادیر بالا، تنش‌های کششی ماکسیمم و مینیمم موجو در صفحه فولادی هستند. در شکل زیر، نحوه توزیع تنش‌ها بر روی سطح مقطع تیر کامپوزیتی مورد تحلیل نمایش داده شده است.

توجه داشته باشید که در سطح اتصال دو ماده، نسبت تنش اعمال شده بر روی سطح فولاد به تنش اعمال شده بر روی سطح چوب برابر است با:

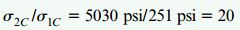
این مقدار با نسبت مدول های الاستیسیته (E₁/E₂) برابری می‌کند. با وجود برابر بودن کرنش‌های موجود در سطح اتصال چوب و فولاد، تنش‌های موجود در هر یک از مواد دارای مقدار متفاوتی است. این تفاوت از اختلاف مدول های الاستیسیته نشات می‌گیرد.

مثال 2

شکل زیر، یک تیر ساندویچی متشکل از یک هسته پلاستیکی و دو صفحه آلومینیومی را نمایش می‌دهد. این تیر در معرض گشتاور خمشی M=3.0kN.m قرار دارد. با فرض ضخامت صفحات آلومینیومی t=5mm، مدول الاستیسیته آلومینیوم E₁=72GPa، ارتفاع هسته پلاستیکی h_c=150mm، مدول الاستیسته پلاستیک E₂=800MPa و ابعاد کلی تیر 160mm*200mm، تنش‌های فشاری و کششی ماکسیمم موجود در صفحات و هسته تیر را با استفاده از روش کلی و تخمینی محاسبه کنید.

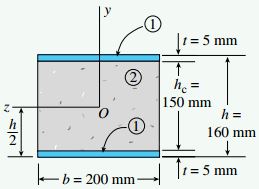
محور خنثی

به دلیل تقارن مضاعف در سطح مقطع تیر مورد بررسی، محور خنثی آن در وسط ارتفاع ( مختصات h/2) قرار خواهد داشت.

ممان اینرسی

مقدار ممان اینرسی I₁ برای سطح مقطع‌های سطوح آلومینیومی از رابطه زیر به دست می‌آید:

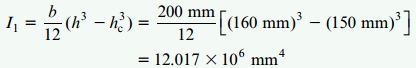
ممان اینرسی I₂ برای هسته پلاستیکی نیز به صورت زیر تعیین می‌شود:

به منظور بررسی صحت این نتایج، مقدار ممان اینرسی کل سطح مقطع حول محور z را محاسبه می‌کنیم. این ممان اینرسی از رابطه I=bh³/12 به دست می‌آید و مقدار آن با حاصل جمع I₁ و I₂ برابر است.

محاسبه تنش‌های نرمال با استفاده از روش کلی

در این بخش، مقدار تنش‌های نرمال را با استفاده از رابطه کلی مورد محاسبه قرار می‌دهیم. به این منظور، ابتدا عبارت موجود در مخرج کسر رابطه مذکور (صلبیت پیچشی) را تعیین می‌کنیم:

تنش‌های فشاری و کششی ماکسیمم اعمال شده بر صفحات آلومینیومی به صورت زیر تعیین می‌شوند:

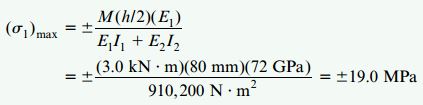
کمیت مربوط به هسته پلاستیکی تیر نیز برابرند با:

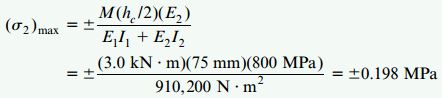
با توجه به نتایج بالا، تنش‌های ماکسیمم موجود در بخش آلومینیومی، 96 برابر بزرگتر از تنش‌های ماکسیمم موجود در بخش پلاستیکی هستند؛ دلیل اصلی این موضوع، نسبت مدول الاستیسیته این دو ماده (E₁/E₂=90) است.

محاسبه تنش‌های نرمال با استفاده از روش تخمینی

بر اساس فرضیات روش تخمینی، هیچ تنش نرمالی به هسته پلاستیکی اعمال نمی‌شود و انتقال تمام گشتاور خمشی از صفحات آلومینیومی صورت می‌گیرد. به این ترتیب، تنش‌های فشاری و کششی ماکسیمم موجود در صفحات به صورت زیر خواهند بود:

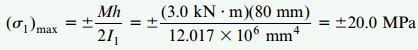
همان گونه که قبلاً نیز اشاره شده، مقدار به دست آمده از روش تخمینی نسبت به مقدار محاسبه شده در روش کلی کوچکتر است. این نتیجه، محافظه کارانه بودن روش تخمینی را نمایش می‌دهد.

^^