تحلیل تیرهای غیر منشوری در شرایط بارگذاری خمشی – با مثال های کاربردی

در مبحث «طراحی تیر در شرایط بارگذاری خمشی»، به معرفی مبانی طراحی تیر در شرایط بارگذاری خمشی (بر اساس رابطه خمش) پرداختیم و چندین مثال کاربردی را نیز مورد بررسی قرار دادیم. روابط به دست آمده در مبحث مذکور برای تیرهای منشوری (سطح مقطع یکنواخت در راستای محور تیر) مورد استفاده قرار گرفتند. با این وجود، در طراحی اتومبیلها، هواپیماها، دستگاهها، پلها، ساختمانها، ابزارآلات و بسیاری از موارد دیگر، مهندسان به منظور کاهش وزن سازه، بهبود عملکرد و ظاهر مناسب آن از تیرهای غیر منشوری استفاده میکنند. در این مقاله، به معرفی کاربرد رابطه خمش برای تعیین تنشهای موجود در تیرهای غیر منشوری خواهیم پرداخت. در انتها نیز به منظور آشنایی بهتر با مفاهیم ارائه شده، چند مثال را تشریح خواهیم کرد.
تیرهای غیر منشوری
اگر تغییر ابعاد مقاطع تیرهای غیر منشوری به صورت تدریجی باشد (مانند مثالهای زیر)، دقت رابطه خمش برای تعیین تنشهای خمشی موجود در این نوع تیرها قابل قبول خواهد بود.

چند مثال از تیرهای غیر منشوری: تیر چراغ برق؛ پل دارای ستون و شاه تیر مخروطی؛ پایه چرخ یک هواپیمای کوچک؛ دسته آچار
نحوه تغییر تنشهای خمشی بر روی محور طولی یک تیر غیر منشوری با یک تیر منشوری تفاوت دارد. به دلیل ثابت بودن مدول مقطع S در یک تیر منشوری، تنشهای موجود متناسب با گشتاور خمشی تغییر میکنند (σ=M/S). اگرچه در یک تیر غیر منشوری، مدول مقطع بر روی محور نیز با تغییر همراه است. به همین دلیل، تنشهای ماکسیمم در سطح مقطع دربرگیرنده گشتاور خمشی ماکسیمم رخ نمیدهند (مانند مثال 1 در انتهای مقاله).
تیر تمام تنیده
برای به حداقل رساندن میزان مواد تشکیلدهنده تیر و کاهش وزن آن، ابعاد سطح مقطع در نقاط مختلف به صورت متغیر طراحی میشوند. نحوه طراحی این تغییرات به گونهای است که حداکثر مقدار مجاز تنش خمشی بر روی هر مقطع رخ میدهد. تیری که در این حالت قرار داشته باشد با عنوان «تیر تمام تنیده» (Fully Stressed Beam) یا «تیر مقاومت ثابت» (Beam of Constant Strength) شناخته میشود.
توجه داشته باشید که به دلیل محدودیتهای اجرایی در ساخت تیرها و احتمال متفاوت بودن بارهای فرضی با شرایط واقعی، دستیابی به شرایط ایدئال به ندرت رخ میدهد. با این اوصاف، شناخت خواص یک تیر تمام تنیده به طراحی سازههایی با حداقل وزن ممکن کمک خواهد کرد. فنرهای شمشی یا تیغهای موجود در اتومبیلها، پلهای دارای شاه تیر و موارد نمایش داده شده در شکل زیر از سازههای شناخته شدهای هستند که برای تحمل تنشهای ماکسیمم طراحی شدهاند.

مثالها
در این بخش به منظور آشنایی با نحوه تحلیل تیرهای غیر منشوری و تعیین شکل تیرهای تمام تنیده، به تشریح دو مثال میپردازیم.
مثال 1
شکل زیر، تیر یکسر گیردار AB با مقطع مخروطی توپر را نمایش میدهد. انتهای آزاد این تیر، بار P را تحمل میکند. نسبت قطر انتهای بزرگ AB به انتهای کوچک آن به صورت زیر است:
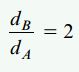
با توجه به اطلاعات مسئله، تنش خمشی σB در تکیهگاه ثابت و تنش خمشی ماکسیمم σmax را محاسبه کنید.
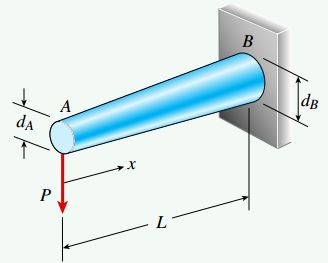
اگر زاویه تغییر سطح مقطع تیر کوچک باشد، مقدار تنشهای به دست آمده از رابطه پیچش تفاوت چندانی با مقدار واقعی نخواهد داشت. به عنوان یک قانون سر انگشتی به خاطر داشته باشید که با اختلاف زاویه 20 درجهای بین خط AB و راستای طولی تیر، خطای محاسبه تنشهای نرمال با استفاده از رابطه پیچش حدود 10 درصد خواهد بود. هر چه زاویه مخروط افزایش یابد، خطا نیز بیشتر میشود.
مدول مقطع
مدول مقطع در هر یک از مقاطع عرضی تیر را میتوان به صورت تابعی از فاصله x نسبت به انتهای آزاد تیر در نظر گرفت. از آنجایی که مدول مقطع به قطر وابسته است، اولین عبارت به صورت زیر نوشته میشود:
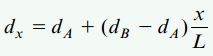
dx: قطر تیر در فاصله x از انتهای آزاد
به این ترتیب، مدول مقطع در فاصله x از انتهای آزاد تیر از رابطه زیر به دست میآید:
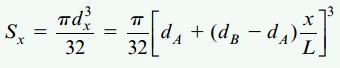
تنشهای خمشی
گشتاور خمشی از رابطه Px به دست میآید. از اینرو، رابطه مورد نیاز برای محاسبه تنش نرمال ماکسیمم در هر یک از مقاطع عرضی تیر به صورت زیر خواهد بود:
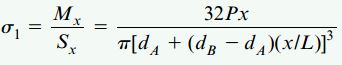
تنش σ1 در بالای تیر به صورت کششی و در پایین آن به صورت فشاری است. توجه داشته باشید که روابط ارائه شده در این بخش برای تمام مقادیر dA و dB با تغییر زاویه کوچک قابل استفاده هستند.
تنش ماکسیمم در تکیهگاه ثابت
تنش ماکسیمم موجود در مقطع دربرگیرنده گشتاور خمشی ماکسیمم (انتهای B) با استفاده از رابطه σ (از بخش قبلی) به دست میآید. به این منظور باید در این رابطه به جای x از L و به جای dB از 2dA استفاده کنیم. با جایگذاری این پارامترها داریم:
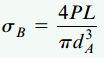
تنش ماکسیمم در تیر
تنش ماکسیمم موجود در مقطعی با فاصله x از انتهای تیر با فرض dB=2dA قابل محاسبه خواهد بود:

به منظور تعیین محل رخ دادن بزرگترین گشتاور خمشی موجود در تیر، در ابتدا باید مقدار x به وجود آورنده بیشترین σ1 را به دست بیاوریم. با مشتقگیری از رابطه σ1 نسبت به x و برابر قرار دادن آن با صفر به معادله زیر میرسیم:
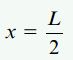
با جایگذاری x=L/2 در رابطه σ1، تنش ماکسیمم مورد نظر ما قابل محاسبه خواهد بود:
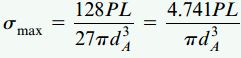
توجه داشته باشید که در این مثال بخصوص، تنش ماکسیمم در مرکز تیر رخ میدهد. به علاوه، این تنش به اندازه 19 درصد از تنش σB در انتهای ثابت تیر بیشتر است. اگر میزان زاویه مخروطی تیر کاهش پیدا کند، محل رخ دادن تنش نرمال ماکسیمم از میانه تیر به سمت تکیهگاه ثابت آن جابجا میشود. برای تیرهای مخروطی با زاویه کوچک، تنش ماکسیمم در انتهای B رخ میدهد.
مثال 2
شکل زیر یک تیر یکسر گیردار با طول L را نمایش میدهد که برای تحمل بار متمرکز P در انتهای آزاد خود طراحی شده است. مقاطع عرضی تیر AB دارای شکل مستطیلی با عرض ثابت b و ارتفاع متغیر h هستند.
به منظور طراحی بهتر تیر، طراحان میخواهند نحوه تغییرات ارتفاع یک تیر ایدئال را مورد بررسی قرار دهند؛ به گونهای که تنش نرمال ماکسیمم در تمام مقطع برابر با تنش مجاز باشد. اگر تنها گشتاور خمشی از رابطه پیچش به دست آوریم، ارتفاع تیر تمام تنیده را تعیین کنید.

گشتاور خمشی و مدول مقطع در فاصله x از انتهای آزاد تیر با استفاده از روابط زیر محاسبه میشوند:

hx: ارتفاع تیر در فاصله x
با جایگذاری عبارات بالا در رابطه پیچش خواهیم داشت:
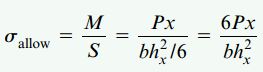
با حل رابطه بالا نسبت به ارتفاع به رابطه زیر میرسیم:
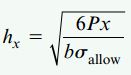
به این ترتیب، در انتهای ثابت تیر (x=L)، ارتفاع hB برابر است با:
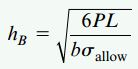
در نتیجه، ارتفاع hx را میتوان به صورت زیر بیان کرد:

رابطه بالا نشان میدهد که تغییرات ارتفاع تیر تمام تنیده با ریشه دوم x رابطه مستقیم دارد. بنابراین، تیر ایدئال مد نظر ما در این مثال دارای شکل سهمیوار است. توجه داشته باشید که در انتهای بارگذاری شده تیر (x=0)، ارتفاع از نظر تئوری برابر با صفر است؛ چراکه هیچ گشتاور خمشی در این نقطه وجود ندارد.
طراحی یک تیر با این شکل کاربردی نیست زیرا این تیر قابلیت تحمل نیروهای برشی در نزدیکی انتهای آزاد را نخواهد داشت. با این اوصاف، شکل ایدئال میتواند شروع خوبی را برای یک طراحی واقعگرایانهتر فراهم کند. در یک طراحی واقعی و کاربردی، اثرات تنشهای برشی و انواع دیگر بارگذاریها نیز در نظر گرفته میشوند.
^^










