کوواریانس و نحوه محاسبه آن — به زبان ساده

یکی از شاخص‌های مهم وابستگی بین دو متغیر تصادفی (Random Variable) در آمار، کوواریانس (Covariance) است. این مفهوم به شکلی با پراکندگی و معیار واریانس (Variance) ارتباط دارد. البته واریانس مربوط به یک متغیر است در حالیکه محاسبه کوواریانس ارتباط بین دو متغیر را بوسیله پراکندگی‌هایشان نسبت به میانگین، نشان می‌دهد. هر چه مقدار کوواریانس بین دو متغیر، بزرگتر باشد، میزان وابستگی بین آن‌ها بیشتر است و برعکس اگر میزان کوواریانس بین دو متغیر کم باشد، وابستگی خطی بین آن‌ها کم خواهد بود. در این نوشتار کوواریانس و نحوه محاسبه آن مورد بحث قرار گرفته است.

به منظور آشنایی بیشتر با مفاهیم مربوط به خصوصیات متغیرهای تصادفی و شاخص‌های مربوطه، بهتر است به عنوان مقدمه، نوشتارهای امید ریاضی (Mathematical Expectation) — مفاهیم و کاربردها و متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کنید. همچنین خواندن وابستگی، کوواریانس و ضریب همبستگی در علم داده — راهنمای کاربردی و ضریب‌های همبستگی (Correlation Coefficients) و شیوه‌ محاسبه آن‌ها — به زبان ساده نیز خالی از لطف نیست.

کوواریانس و نحوه محاسبه آن

اغلب برای مشخص کردن میزان رابطه خطی بین دو متغیر تصادفی از کوواریانس استفاده می‌شود. مقدار کوواریانس دو متغیر، شامل مقادیر مثبت و منفی است. ولی هر چه مقدار کوواریانس به صفر نزدیکتر باشد، میزان وابستگی خطی بین آن‌ها کمتر خواهد بود. مقادیر مثبت نشانگر رابطه هم جهت بین دو متغیر و مقادیر منفی کوواریانس نیز بیانگر رابطه معکوس بین آن‌ها خواهد بود.

فیلم آموزش درس رگرسیون 1 – رگرسیون خطی در فرادرس

کلیک کنید

البته باید به این موضوع توجه داشت که کوواریانس و نحوه محاسبه آن (بدون در نظر گرفتن علامت)، شدت رابطه را مشخص نمی‌کند زیرا این شاخص به واحد اندازه‌گیری هر یک از متغیرها وابسته است. در نتیجه محاسبه کوواریانس با تغییر واحد اندازه‌گیری هر یک از متغیرها، متفاوت خواهد بود.

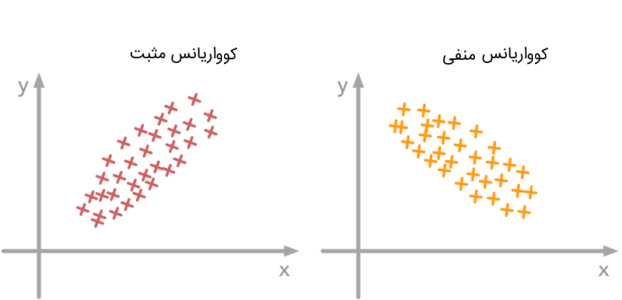
برای مثال متغیری که طول را نشان می‌دهد ممکن است با واحدهای مختلفی اندازه‌گیری شود. اگر واحد این متغیر از میلی‌متر یا سانتی‌متر به کیلومتر تغییر کند، کوواریانس کاهش خواهد یافت، زیرا اعداد مربوط به محاسبه طول کوچکتر می‌شوند و برعکس اگر طول را به جای اندازه‌گیری برحسب کیلومتر برحسب میلی‌متر مشخص کنیم، کوواریانس متغیر طول نسبت به هر متغیر دیگری، افزایش زیادی خواهد داشت.

به همین دلیل برای مقایسه رابطه بین جفت متغیرها از کوواریانس استفاده نمی‌شود، مگر آنکه مقادیر متغیرها را به صورت استاندارد و بدون واحد در آورده، سپس محاسبه کوواریانس را انجام دهیم.

تعریف کوواریانس و نحوه محاسبه آن برای دو متغیر تصادفی

تابع توزیع توام دو متغیر تصادفی $$X$$‌ و $$Y$$ را در نظر بگیرید. بر اساس این توزیع توام، قادر به محاسبه کوواریانس هستیم. البته فرض وجود گشتاور دوم متناهی برای این متغیرها نیز باید وجود داشته باشد. به این ترتیب کوواریانس، میانگین حاصل‌ضرب فاصله هر یک از متغیرهای تصادفی از میانگین‌شان تعریف می‌شود. با توجه به این تعریف، شیوه محاسبه کوواریانس برای متغیرهای تصادفی حقیقی‌-مقدار مطابق با رابطه ۱ خواهد بود.

$$\large {\displaystyle \operatorname {cov} (X,Y) = \operatorname {E} {{\big [}(X - \operatorname {E} [X])(Y -\operatorname {E} [Y]){ \big ]}},}$$

رابطه (۱) کوواریانس و نحوه محاسبه آن برای متغیرهای تصادفی $$X$$ و $$Y$$

فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس

کلیک کنید

که در آن $$\operatorname{E}(X)$$ و $$\operatorname{E}(Y)$$ امید ریاضی یا مقدار چشم‌داشتی هر یک از متغیرهای $$X$$ و $$Y$$ هستند.

همانطور که مشخص است کوواریانس، یک شاخص متقارن است به این معنی که $$\operatorname{cov} (X,Y) = \operatorname{cov} (Y,X)$$. برای محاسبه کوواریانس شاید بهتر باشد که از رابطه ساده‌تری که در ادامه مشخص شده است، کمک گرفت. رابطه ۲ مشخص می‌کند که کوواریانس، تفاضل حاصل ضرب امید ریاضی هر یک از متغیرها از امید ریاضی حاصل‌ضرب آن‌ها است. به این ترتیب رابطه زیر اثباتی است که برمبنای رابطه ۱ نوشته شده و سادگی در انجام محاسبات را به همراه دارد.

$$\large {\displaystyle {\begin{aligned}\operatorname {cov} (X,Y)&=\operatorname {E} \left[\left(X-\operatorname {E} \left[X\right]\right)\left(Y-\operatorname {E} \left[Y\right]\right)\right]\\&=\operatorname {E} \left[XY-X\operatorname {E} \left[Y\right]-\operatorname {E} \left[X\right]Y + \operatorname {E} \left[ X \right] \operatorname {E} \left[ Y \right] \right]\\ & =\operatorname {E} \left[ XY \right] - \operatorname {E} \left[ X \right] \operatorname {E} \left[Y \right] - \operatorname {E} \left[ X \right] \operatorname {E} \left[ Y \right] + \operatorname {E} \left[ X \right]\operatorname {E} \left[Y\right]\\ &= \operatorname {E} \left[ XY \right] - \operatorname {E} \left[ X \right] \operatorname {E} \left[Y\right],\end{aligned}}}$$

رابطه (۲) کوواریانس و نحوه محاسبه آن برحسب امید ریاضی حاصل‌ضرب متغیرهای تصادفی

نکته: شیوه محاسبه ارائه شده در رابطه ۲، ممکن است برای مقادیر بسیار نزدیک از متغیرهای تصادفی، دچار خطا گردد. این موضوع بخصوص برای برنامه‌ها رایانه‌ای ممکن است با خطای زیاد در کوواریانس و نحوه محاسبه آن همراه باشد.

واضح است که واحد یا مقیاس برای کوواریانس، برحسب حاصل‌ضرب واحدهای دو متغیر تصادفی ساخته می‌شود. برای مثال اگر بخواهیم وابستگی بین دو متغیر تصادفی طول و وزن را مشخص کنیم، اگر طول با واحد متر و وزن با واحد کیلوگرم مشخص شده باشد، واحد شاخص کوواریانس برابر با متر در کیلوگرم خواهد بود. گاهی برای نمایش کوواریانس از نمادهای $$\sigma_{XY}$$ یا $$\sigma(X,Y)$$ هم استفاده می‌شود.

مثال ‍۱

جفت متغیرهای تصادفی $$(X,Y)$$ را با مقادیر $$(x_i,y_i)$$ در نظر بگیرید که $$i = 1 , \ldots, n$$ و تابع توزیع توام نیز به شکل $$p_i = 1/n$$ است. براساس تعریفی که در رابطه ۱ بیان شد، کوواریانس بین این دو متغیر به شکل زیر محاسبه خواهد شد.

$$\large { \displaystyle \operatorname {cov} (X,Y) = { \frac {1}{n}}\sum _{ i = 1 }^{ n }( x_{i} - E(X))(y_{i} - E(Y))}$$

به این ترتیب با کمی ساده‌سازی و محاسبه میانگین مقادیر به جای امید ریاضی به رابطه زیر خواهیم رسید.

$$\large {\displaystyle \operatorname {cov} (X,Y)={\frac {1}{n^{2}}}\sum _{i = 1}^{n} \sum _{j=1}^{n}{\frac {1}{2}}(x_{i}-x_{j})(y_{i}-y_{j})={ \frac {1}{n^{2}}}\sum _{i}\sum _{j>i}(x_{i}-x_{j})(y_{i}-y_{j})}$$

به طور کلی اگر توزیع توام دو متغیر تصادفی گسسته به شکل $$p_i$$ باشد، کوواریانس بین آن دو به شکل زیر محاسبه خواهد شد.

$$\large {\displaystyle \operatorname {cov} (X,Y)=\sum _{i=1}^{n}p_{i}(x_{i}-E(X))(y_{i}-E(Y))}$$

مثلا توزیع توام دو متغیر تصادفی $$X$$ و $$Y$$ را مطابق با تکیه‌گاه ذکر شده، به شکل زیر در نظر بگیرید.

$$\large { \displaystyle (x,y) \in S = \left\{ (1,1) , (1,2) , (1,3) , (2,1) , (2,2) , (2,3) \right \}}$$

جدول ۱: توزیع توام متغیرهای تصادفی $$X$$ و $$Y$$

همانطور که جدول ۱، نمایش می‌دهد، مقادیر $$X$$ برابر با مجموعه ۱ و ۲ بوده و متغیر $$Y$$ نیز مقادیر ۱ و ۲ و ۳ را خواهد پذیرفت. میانگین (امید ریاضی) برای متغیر تصادفی $$X$$ نیز برابر با $$\mu_X = 3/2$$ و برای متغیر تصادفی $$Y$$ نیز $$\mu_Y=2$$ خواهد بود. انحراف استاندارد این متغیرهای تصادفی نیز به ترتیب برابر با $$\sigma_X = 1/2 , \sigma_Y = \sqrt{\frac{1}{2}}$$ محاسبه می‌شود. در نتیجه کوواریانس این دو متغیر را به شکل زیر بدست خواهیم آورد.

$$\large {\displaystyle {\begin{aligned}\operatorname {cov} (X,Y)={}&\sigma _{XY}=\sum _{(x,y)\in S}f(x,y)(x-\mu _{X})(y-\mu _{Y})\\[4pt] \large ={}&\left({\frac {1}{4}}\right)\left(1 - { \frac {3}{2}} \right)(1-2) + \left( { \frac {1}{4}}\right)\left(1 -{ \frac {3}{2}}\right)(2-2)\\[4pt] \large &{} + (0) \left( 1 - { \frac {3}{2}} \right) ( 3 - 2 ) + ( 0 ) \left( 2 - { \frac {3}{2}} \right) ( 1 - 2 ) \\[4pt] \large &{} + \left( { \frac {1}{4}} \right) \left( 2 - { \frac {3}{2}} \right)( 2 - 2 ) + \left({ \frac {1}{4}} \right) \left( 2 - { \frac {3}{2}} \right) ( 3 - 2 ) \\[4pt] \large = {}& { \frac {1} {4}} \end{aligned}}}$$

کوواریانس و نحوه محاسبه آن برای متغیرهای تصادفی با مقادیر مختلط

فرض کنید متغیرهای تصادفی $$W$$ و $$Z$$ با مقادیر مختلط باشند. در این صورت کوواریانس بین آن دو توسط رابطه ۳ محاسبه و بدست خواهد آمد.

$$\large {\displaystyle \operatorname {cov} (Z,W) = \operatorname {E} [(Z - \operatorname {E} [Z]){ \overline {(W - \operatorname {E} [W])}}] = \operatorname {E} [Z{ \overline {W}}] - \operatorname {E} [Z] \operatorname {E} [{ \overline {W}}]}$$

رابطه (۳) کوواریانس و نحوه محاسبه آن برای متغیرها تصادفی با مقادیر مختلط

مشخص است که منظور از $$\overline{W}$$ مزدوج مختلط متغیر تصادفی $$W$$ است.

خصوصیات کوواریانس و نحوه محاسبه آن

در ادامه به بعضی از خصوصیات جالب کوواریانس خواهیم پرداخت. البته توجه داشته باشید که کوواریانس به وابستگی خطی بین دو متغیر اشاره دارد.

فیلم آموزش آنالیز واریانس با اس پی اس اس SPSS در فرادرس

کلیک کنید

• کوواریانس هر متغیر تصادفی با خودش، همان واریانس خواهد بود. به این ترتیب رابطه زیر برقرار است. مشخص است که این موضوع به کمک رابطه ۱ به خوبی قابل مشاهده است.

$$\large { \displaystyle \operatorname {cov} (X,X) = \operatorname {var} (X) \equiv \sigma ^{2}(X) \equiv \sigma _{X}^{2}}$$

• کوواریانس ترکیب خطی از متغیرهای تصادفی نیز به شکل زیر محاسبه می‌شود. فرض بر این است که $$X , Y , V , W$$ چهار متغیر تصادفی هستند که توزیع توام دو به دوی آن‌ها نیز موجود است و $$a,b,c,d,$$ نیز اعداد حقیقی هستند.

$$\large { \displaystyle { \begin{aligned} \operatorname {cov} (X,a)&=0\\ \large \operatorname {cov} ( X , X )& = \operatorname {var} (X) \\ \large \operatorname {cov} (X,Y)& = \operatorname {cov} (Y,X)\\ \large \operatorname {cov} (aX,bY)& = a b \, \operatorname {cov} ( X , Y ) \\ \large \operatorname {cov} (X + a , Y + b ) & = \operatorname {cov} ( X , Y ) \\ \large \operatorname {cov} (a X + b Y , c W + d V ) & = ac \,\operatorname {cov} (X , W ) + a d \,\operatorname {cov} ( X , V ) + b c \, \operatorname {cov} ( Y , W) + b d \, \operatorname {cov} ( Y , V ) \end{aligned}}}$$

رابطه خطی را برای یک دنباله از متغیرهای تصادفی نیز می‌توان تعمیم داد. در این حالت اگر $$X_1, \ldots, X_n$$ یک دنباله از متغیرهای تصادفی با یک تابع توزیع توام مشخص باشد و $$a_1, \ldots, a_n$$ نیز اعداد حقیقی در نظر گرفته شوند، آنگاه رابطه زیر بین کوواریانس زوج‌ متغیرها و واریانس ترکیب خطی از آن‌ها برقرار خواهد بود.

$$ \large { \displaystyle \sigma ^{2} \left( \sum _{ i = 1 }^{ n } a_{i} X_{i} \right) = \sum _{i=1}^{n} a_{i}^{2} \sigma ^{2}(X_{i}) + 2  \sum _{i,j\,:\,i<j} a_{i} a_{j} \operatorname {cov} (X_{i} , X_{j}) = \sum _{i,j} {a_{i} a_{j} \operatorname {cov} (X_{i} , X_{j})}} $$

• نامساوی هوفدینگ برای کوواریانس (Hoeffding's Covariance Identity) نیز به شکل زیر نوشته می‌شود.

$$\large {\displaystyle \operatorname {cov} (X,Y)=\int _{\mathbb {R} }\int _{\mathbb {R} }(F_{(X,Y)}(x,y)-F_{X}(x)F_{Y}(y))\,dx\,dy}$$

که در آن $$F_X(x)$$ تابع توزیع تجمعی (CDF) متغیر تصادفی $$X$$ است و $$F_{X,Y}(x,y)$$ نیز توزیع توام تجمعی متغیرهای تصادفی $$X$$ و $$Y$$ است.

• کوواریانس متغیرهای تصادفی ناهمبسته صفر است. در حقیقت دو متغیر تصادفی را ناهمبسته (Uncorrelated) می‌نامند اگر مقدار کوواریانس بین آن‌ها صفر باشد. از طرفی برای دو متغیر تصادفی مستقل نیز مقدار کوواریانس صفر خواهد بود. این موضوع در رابطه زیر مشخص شده است.

$$\large {\displaystyle \operatorname {E} [XY]=\operatorname {E} [X]\cdot \operatorname {E} [Y]}$$

• کوواریانس صفر دلیلی بر مستقل بودن دو متغیر نیست. در واقع عکس عبارت بالا همیشه صحیح نخواهد بود. به این معنی که اگر مقدار کوواریانس برابر با صفر باشد، دلیلی بر مستقل بودن دو متغیر نمی‌توان ارائه کرد. برای مثال فرض کنید $$Y=X^2$$ و $$X \sim Uniform[-1,1]$$ باشد. آنگاه می‌توان به وسیله روابط زیر نشان داد که کوواریانس بین این دو متغیر تصادفی صفر است در حالیکه مشخص است $$Y$$ مستقل از $$X$$ نیست. البته این نکته را هم باید در نظر گرفت که صفر بودن کوواریانس بین دو متغیر با شرط توزیع توام نرمال، نشانگر استقلال آن دو خواهد بود.

$$\large { \displaystyle {\begin{aligned} \operatorname {cov} ( X , Y ) & = \operatorname {cov} (X , X^{2}) \\ & = \operatorname {E} [X\cdot X^{2}] - \operatorname {E} [X] \cdot \operatorname {E} [X^{2}]\\ \large & = \operatorname {E} \left[ X ^{3} \right] - \operatorname {E} [X]\operatorname {E} [X^{2}]\\& = 0 - 0 \cdot \operatorname {E} [X^{2}] \\ & \large =0 \end{aligned}}}$$

کوواریانس و نحوه محاسبه آن براساس ضرب داخلی دو بردار تصادفی

بسیاری از خواص کوواریانس و نحوه محاسبه آن را به واسطه ضرب داخلی دو بردار (Inner Product) می‌توان مشخص کرد. برای مثال می‌توان به رابطه تقارن در کوواریانس اشاره کرد که کاملا شبیه ضرب داخلی است. همچنین حفظ رابطه خطی بین متغیر یا بردارهای تصادفی نیز از ویژگی‌های دیگری است که در ضرب داخلی نیز وجود دارد. از طرفی دیدیم که کوواریانس هر متغیر تصادفی با خودش، واریانس را مشخص می‌کند. این امر نشانگر نامنفی بودن کوواریانس متغیر تصادفی با خودش است زیرا حاصل واریانس متغیر تصادفی را نشان می‌دهد. این امر نیز در ضرب برداری دیده می‌شود. ضرب داخلی هر بردار در خودش، نیمه معین مثبت (Positive Semi-Definite) است.

به این ترتیب می‌توان کوواریانس و نحوه محاسبه آن را مشابه ضرب داخلی دو بردار تصادفی در نظر گرفت. به کمک این خصوصیت می‌توان با استفاده از نامساوی کوشی-شوارتز (Cauchy-Schwartz Inequality) برای بردارها و ضرب داخلی آن‌ها، خاصیت جالبی را برای کوواریانس مشخص کرد و یک کران بالا برای کوواریانس دو متغیر تصادفی ایجاد کرد. این موضوع در رابطه زیر دیده می‌شود.

$$\large { \displaystyle | \operatorname {cov} ( X , Y) | \leq { \sqrt {\sigma ^{2}( X )\sigma ^{2}( Y )}}}$$

رابطه بالا به شرط متناهی بودن واریانس دو متغیر تصادفی برقرار است. اثبات این نامساوی به شکل زیر صورت می‌گیرد.

اگر $$\sigma^2_Y=0$$، به طور وضوح، نامساوی برقرار است (این موضوع را در اولین خاصیت ترکیب خطی کوواریانس معرفی کردیم که کوواریانس متغیر تصادفی با مقدار ثابت برابر با صفر است). حال وضعیتی را در نظر بگیرید که در آن متغیر تصادفی $$Z$$ به شکل زیر تعریف شده است.

$$\large {\displaystyle Z=X-{\frac {\operatorname {cov} (X,Y)}{\sigma ^{2}(Y)}}Y}$$

در نتیجه خواهیم داشت:

$$\large {\displaystyle {\begin{aligned} 0 \leq \sigma ^{2}(Z) & = \operatorname {cov} \left(X - { \frac { \operatorname {cov} (X , Y )}{ \sigma ^{2}(Y)}}Y , X - { \frac { \operatorname {cov} (X,Y )}{ \sigma ^{2}(Y)}}Y \right) \\[12pt] & \large =\sigma ^{2}(X) - { \frac {( \operatorname {cov} ( X , Y ))^{2}}{\sigma ^{2}( Y )}} \end{aligned}}}$$

همانطور که مشخص است به راحتی کران بالا برای کوواریانس دو متغیر برحسب حاصل ضرب واریانس هر یک ساخته شد.

کوواریانس و نحوه محاسبه آن برای یک نمونه تصادفی

کوواریانس نمونه‌ای برای $$K$$ متغیر تصادفی و با $$N$$ نمونه تصادفی برگرفته از جامعه آماری تشکیل یک ماتریس $$K \times K$$ می‌دهد که هر یک از مولفه‌های آن به شکل زیر حاصل می‌شوند.

$$\large {\displaystyle q_{jk} = { \frac {1}{N-1}} \sum _{i = 1}^{N} \left( X_{ij}-{\overline { X }}_{j}\right) \left( X_{ik} - {\overline {X}}_{k}\right) }$$

فیلم آموزش تجزیه و تحلیل اطلاعات با نرم افزار SAS ساس در فرادرس

کلیک کنید

این مولفه‌ها، برآوردی برای کوواریانس مولفه‌ای جامعه آماری محسوب می‌شوند. حتما توجه دارید که در مخرج کسر از $$N-1$$ استفاده شده تا برآوردگرهای حاصل، نااریب (Unbiased) باشند زیرا می‌دانیم برای محاسبه کوواریانس باید عمل برآورد را هم برای میانگین جامعه آماری انجام داده، در نتیجه یک واحد از درجه آزادی (Degree of Freedom) کسر خواهد شد. البته توجه داشته باشید که اگر میانگین جامعه آماری مشخص باشد، نحوه محاسبه کوواریانس نمونه‌ای به شکل زیر درخواهد آمد. مشخص است که این بار مخرج کسر برابر با $$N$$ است و از درجه آزادی، مقداری کاسته نخواهد شد.

$$\large {\displaystyle q_{jk} = { \frac {1}{N}} \sum _{ i = 1 }^{N} \left(X_{ij} - \operatorname {E} (X_{j}) \right) \left(X_{ik} - \operatorname {E} (X_{k}) \right) }$$

به این ترتیب هر گاه براساس نمونه بخواهیم کوواریانس و نحوه محاسبه آن را به درستی مشخص کنیم از رابطه اخیر کمک خواهیم گرفت.

ماتریس واریانس-کوواریانس بردارهای تصادفی

در قسمت قبل، مبنای محاسبات، متغیرهای تصادفی بودند که واریانس ثابت و متناهی داشتند. در این حالت نحوه محاسبه کوواریانس و کاربردهای آن را مرور کردیم. ولی در این جا بردارهای تصادفی ملاک هستند و براساس آن‌ها می‌خواهیم ماتریس کوواریانس را بدست آوریم. ابتدا ماتریس کوواریانس یک بردار تصادفی سپس ماتریس کوواریانس بین دو بردار تصادفی را مرور خواهیم کرد.

ماتریس کوواریانس و نحوه محاسبه آن برای بردار تصادفی

در حالت چند متغیره نیز کوواریانس و نحوه محاسبه آن برایمان مهم است زیرا اغلب با پدیده‌های مواجه هستیم که بین ویژگی یا متغیرهای آن رابطه‌ای وجود دارد. یک بردار تصادفی $$m$$-بُعدی مثل $$X = [X_1.X_2,\ldots,X_m]^T$$ که تشکیل شده از $$m$$ متغیر تصادفی با توزیع توام $$f$$ و گشتاور دوم متناهی را در نظر بگیرید. «ماتریس کوواریانس» (Covariance Matrix) که گاهی به آن «ماتریس واریانس-کوواریانس» (Variance-Covariance Matrix) نیز گفته می‌شود با نماد $$\Sigma_X$$ یا $$K_{XX}$$ نشان داده شده و به صورت زیر محاسبه می‌شود.

$$\large {\displaystyle {\begin{aligned} \operatorname {K} _{\mathbf {X} \mathbf {X} } = \operatorname {cov} (\mathbf {X} ,\mathbf {X} )& = \operatorname {E} \left[( \mathbf {X} - \operatorname {E} [ \mathbf {X} ])(\mathbf {X} - \operatorname {E} [\mathbf {X} ])^{\mathrm {T} } \right]\\ & = \operatorname {E} \left[ \mathbf {X} \mathbf {X} ^{\mathrm {T} } \right]- \operatorname {E} [ \mathbf {X} ] \operatorname {E} [ \mathbf {X} ]^{\mathrm {T} }.\end{aligned}}}$$

توجه داشته باشید که علامت $$^T$$‌ همان ترانهاده ماتریس در نظر گرفته شده است.

فیلم آموزش همبستگی و رگرسیون خطی در اس پی اس اس SPSS در فرادرس

کلیک کنید

با توجه به تعریفی که از ماتریس واریانس-کوواریانس $$\Sigma$$ ارائه شد، می‌توانیم ترکیب خطی از این بردار را در نظر گرفته و کوواریانس حاصل از ترکیب خطی را هم به مانند حالت تک متغیره محاسبه کنیم. فرض کنید که $$A$$ یک ماتریس باشد که قابلیت ضرب در بردار تصادفی را از چپ داشته باشد. واضح است که $$A$$ شامل ضرایب ترکیب خطی است. در این صورت محاسبه ماتریس کوواریانس $$AX$$ به شکل زیر خواهد بود.

$$\large {\displaystyle \Sigma (\mathbf {A} \mathbf {X} )=\operatorname {E} [\mathbf {A} \mathbf {X} \mathbf {X} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }]-\operatorname {E} [\mathbf {A} \mathbf {X} ]\operatorname {E} [\mathbf {X} ^{\mathrm {T} }\mathbf {A} ^{\mathrm {T} }]=\mathbf {A} \Sigma \mathbf {A} ^{\mathrm {T} }}$$

رابطه بالا براساس خاصیت خطی بودن امید ریاضی است و می‌تواند بخصوص برای تبدیلات خطی بردارها مانند تبدیل کروی (Sphering Transformation) اشاره کرد که توسط آن یک بردار با ماتریس کوواریانس مشخص، تبدیل به برداری‌های ناهمبسته با واریانس واحد می‌شود. معمولا این تبدیل را با نام «تبدیل سفیدگر» (Whiting Transformation) نیز می‌شناسند زیرا بردار ورودی را تبدیل به برداری از نویزهای سفید خواهد کرد که دارای واریانس واحد بوده و از هم مستقل هستند.

ماتریس کوواریانس و نحوه محاسبه آن برای بردارهای تصادفی با مقادیر حقیقی

این بار بردارهای $$X$$ و $$Y$$ را در نظر بگیرید که متعلق به یک فضای برداری هستند بطوری که $$X \in R^m$$ و $$Y \in R^n$$ آن‌ها را مشخص کرده است. در این صورت «ماتریس کوواریانس متقاطع» (Cross-Covariance Matrix)، دارای $$m$$ سطر و $$n$$ ستون بوده و به شکل زیر محاسبه می‌گردد.

$$\large { \displaystyle { \begin{aligned} \operatorname {K} _{ \mathbf {X} \mathbf {Y} }= \operatorname {cov} (\mathbf {X} , \mathbf {Y} )& = \operatorname {E} \left[( \mathbf {X} - \operatorname {E} [ \mathbf {X} ])( \mathbf {Y} - \operatorname {E} [ \mathbf {Y} ])^{ \mathrm {T} } \right] \\ & = \operatorname {E} \left[ \mathbf {X} \mathbf {Y} ^{ \mathrm {T} }\right] - \operatorname {E} [ \mathbf {X} ] \operatorname {E} [ \mathbf {Y} ]^{ \mathrm {T} } \end{aligned}}}$$

در رابطه بالا $$Y^T$$ ترانهاده بردار یا ماتریس $$Y$$ است. هر یک از عناصر این ماتریس، کوواریانس بین متغیری از بردار $$X$$ و $$Y$$ را نشان می‌دهد. برای مثال عنصر سطر $$i$$ام و ستون $$j$$ام برابر با $$Cov(X_i,Y_j)$$ است که همان کوواریانس بین متغیر تصادفی $$i$$ از بردار $$X$$ و متغیر تصادفی $$j$$ام از بردار تصادفی $$Y$$ است.

نکته: توجه داشته باشید که به علت خاصیت جابجایی در ضرب برای امید ریاضی، ماتریس کوواریانس بردارهای تصادفی، متقارن است. به این معنی که ترانهاده ماتریس کوواریانس با خود ماتریس کوواریانس برابر است.

$$\large Cov(X,Y) = Cov(Y,X)$$

تاریخچه کوواریانس و نحوه محاسبه آن

«کارل پیرسون» (Carl Pearson) دانشمند و ریاضیدان انگلیسی، که «ضریب همبستگی خطی پیرسون» (Pearson Correlation) را به نام خود ثبت کرده است به بررسی رابطه خطی بین دو متغیر پرداخت. او وضعیتی را در نظر گرفت که دو متغیر به صورت خطی با یکدیگر در ارتباط بودند. متغیر اول را $$X$$ و متغیر دوم را $$Y$$ در نظر بگیرید. نقاط حاصل از این دو متغیر در صفحه مختصات دکارتی را به صورت زوج‌های مرتب $$(x_i,y_i)$$ مشخص می‌کنیم. پیرسون که مبدع روش رگرسیون (Regression) هم محسوب می شود، توانست ضریبی را برای نشان دادن میزان وابستگی خطی بین دو متغیر معرفی کند. او مشخص کرد که خط رگرسیونی از میانگین $$X$$ و $$Y$$ یعنی نقطه $$(\overline{X}, \overline{Y})$$ می‌گذرد.

فیلم مجموعه آموزش آمار و احتمالات – از دروس دانشگاهی تا کاربردی در فرادرس

کلیک کنید

بنابراین اگر بخواهیم معادله خط رگرسیونی را بنویسیم می‌توانیم با کمک دو نقطه از این خط، ضرایب را مشخص کنیم. یکی از نقطه‌ها را $$(x_i,y_i)$$ و دیگری را همان $$(\overline{X},\overline{Y})$$ در نظر می‌گیریم. پس خواهیم داشت:

$$\large Y-\overline{Y} = \dfrac{Y_i-\overline{Y}}{X_i-\overline{X}}(X-\overline{X})$$

با طرفین وسطین کردن این رابطه به معادله زیر خواهیم رسید.

$$\large (Y-\overline{Y})(X_i-\overline{X}) = (Y_i-\overline{Y})(X-\overline{X})$$

همانطور که مشاهده می‌کنید، این جمله بسیار به کوواریانس و نحوه محاسبه آن برحسب رابطه ۱، شبیه است. اگر نقاط $$X_i$$ و $$Y_i$$ را که $$i =1 , 2, \ldots, n$$ بوده و حتما در این رابطه صدق می‌کنند به جای $$X$$ و $$Y$$ قرار دهیم پس از میانگین‌گیری، به فرمول کوواریانس خواهیم رسید.

$$\large \sum_{i=1}^n (Y_i-\overline{Y})(X_i-\overline{X}) = \sum_{i=1}^n (Y_i-\overline{Y})(X_i-\overline{X})$$

به همین علت گفته می‌شود که کوواریانس میزان وابستگی خطی بین دو متغیر را مشخص می‌کند. البته می‌دانیم که ضریب همبستگی نیز حالتی از نرمال شده کوواریانس و نحوه محاسبه آن نیز هست. هر چه وابستگی خطی بین دو متغیر بیشتر باشد، ضریب همبستگی پیرسون به ۱ یا ۱- نزدیک‌تر خواهد بود و در صورت وجود رابطه خطی کامل بین آن‌ها، ضریب همبستگی برابر با ۱ یا ۱- می‌شود.

کاربردهای کوواریانس

کوواریانس و نحوه محاسبه آن کاربردهای زیادی برای نمایش یا بررسی میزان وابستگی خطی بین متغیرها یا بردارهای تصادفی دارد. در ادامه این متن به بعضی از آن‌ها اشاره خواهیم کرد.

• در ژنتیک و بیولوژی مولکولی از کوواریانس برای نمایش وابستگی بین توالی‌های ژن‌ها و پرونئین‌ها استفاده می‌شود. به این ترتیب برای کوواریانس و نحوه محاسبه آن نقش مهمی در تهیه «ماتریس رابطه ژنتیک» (Genetic Relation matrix) دارد. این ماتریس در توصیف توالی DNA‌ها به کار می‌رود.
• در حوزه علوم مالی و اقتصاد نیز کوواریانس و نحوه محاسبه آن برای نمایش وابستگی خطی بین متغیرها به کار می‌رود. در ایجاد مدل‌های قیمت‌گذاری دارایی سرمایه‌ای کوواریانس نقش مهمی ایفا می‌کند. به این ترتیب میزان وابستگی بین دارایی‌ها که توسط کوواریانس محاسبه می‌شوند سبد سرمایه‌گذاری مناسبی را تشکیل دهند.
• ماتریس کوواریانس و نحوه محاسبه آن برای استخراج ویژگی (Feature Extraction) نیز به کار می‌رود. به این ترتیب متغیرهایی که وابستگی کمتری با یکدیگر داشته و بیشترین توصیف را از مشاهدات در خود داشته باشند، پیدا و برای تحلیل‌های آماری به کار می‌برند.
• ماتریس کوواریانس در برآورد شرایط اولیه مورد نیاز برای اجرای مدل‌های پیش بینی وضعیت هوا، مورد استفاده قرار می‌گیرد. در روشی که معروف به جذب داده‌ها (Data Assimilation) است،  «ماتریس کواریانس خطای پیش بینی» (Forecast Error Covariance Matrix) به طور معمول ارتباط بین آشفتگی‌های دما و دیگر ویژگی‌های آب و هوایی با یک نقطه معیار (که معمولا میانگین در نظر گرفته می‌شود) را نشان می‌دهد. واضح است که ماتریس همان کوواریانس بین متغیرها است. مقادیر روی قطر اصلی این ماتریس همان پراکندگی یا واریانس بوده و عناصر خارج از قطر هم وابستگی خطی یا کوواریانس بین متغیرها را نشان می‌دهد. این ماتریس کاربردهای گسترده‌ای در به کارگیری فیلتر کالمن (Kalman Filter) بخصوص در سیستم‌های وابسته به زمان دارد.

خلاصه و جمع‌بندی

در این نوشتار با کوواریانس و نحوه محاسبه آن آشنا شدیم. به کمک مثال‌هایی که ارائه شد، محاسبات مربوط به کوواریانس نیز مرور شدند. خصوصیات و نحوه بدست آوردن ماتریس کوواریانس نیز از مواردی بود که در این متن به آن‌ها پرداختیم. همانطور که اشاره شد، کوواریانس میزان رابطه خطی بین دو متغیر یا بردارهای تصادفی را نمایش و محاسبه می‌کند. مقدار نرمال شده کوواریانس نیز به نام ضریب همبستگی (Correlation Coefficient) در بازه ۱ یا ۱- تغییر کرده که برای مقایسه شدت رابطه خطی بین زوج متغیرهای مختلف، مناسب‌تر است.