پوش منحنی — از صفر تا صد (+ دانلود فیلم آموزش رایگان)

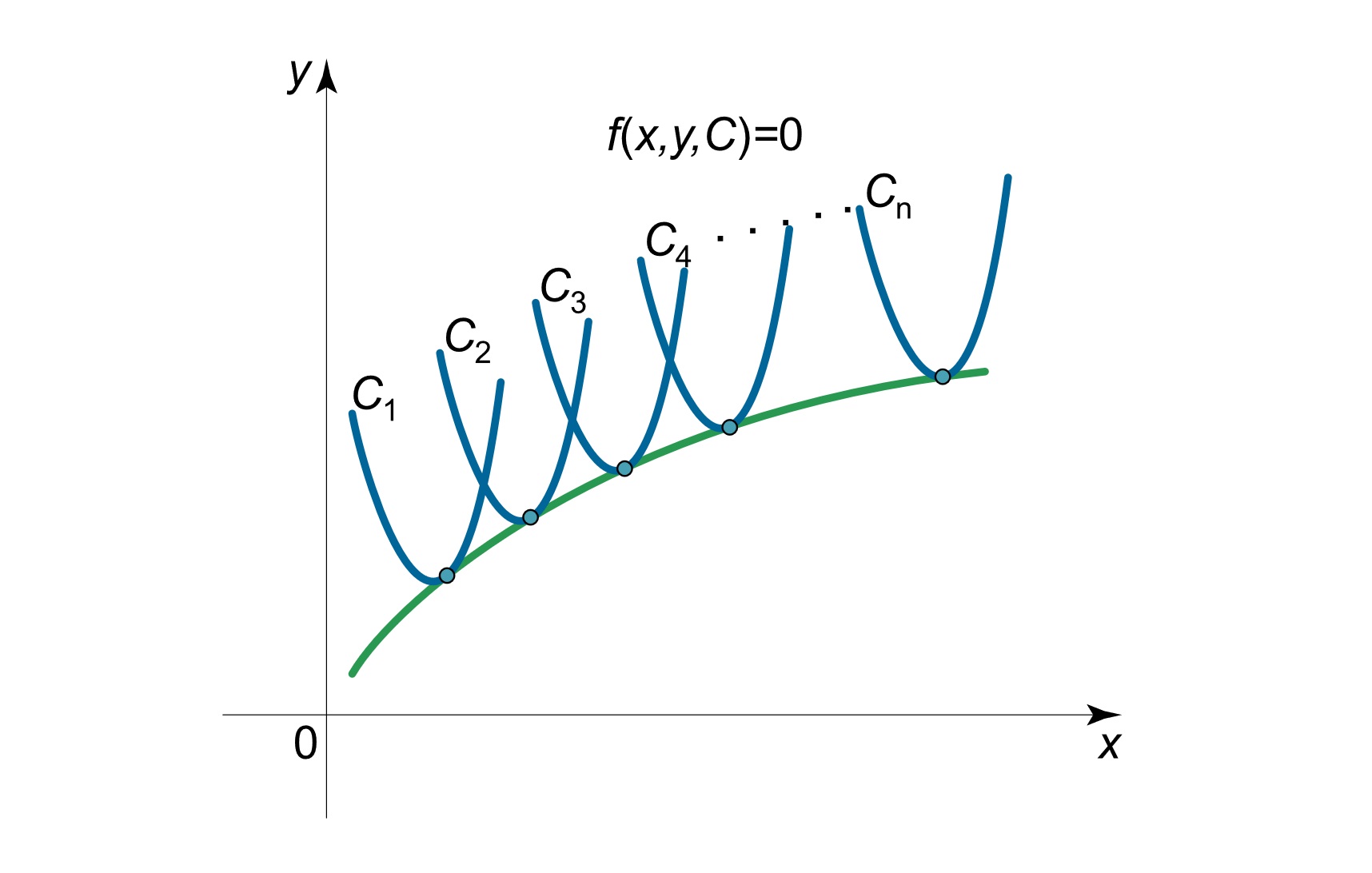
پوش دسته منحنی‌‌ها، یک منحنی است که در هر نقطه با یکی از منحنی‌‌های دسته به طور مماس تماس پیدا می‌‌کند. در ادامه مجموعه آموزش‌های ریاضی مجله فرادرس، در این آموزش با پوش منحنی و نحوه به دست آوردن معادله آن آشنا می‌شویم.

پوش منحنی

دسته منحنی‌‌های صفحه‌‌ای یک پارامتری را در نظر بگیرید که با معادله زیر توصیف می‌شوند:

$$ \large f \left ( { x , y, C } \right ) = 0 , $$

که در آن، $$C$$ یک پارامتر است.

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

پوش این دسته منحنی‌‌ها، یک منحنی است که در هر نقطه با یکی از منحنی‌‌های دسته به طور مماس تماس پیدا می‌‌کند (شکل 1).

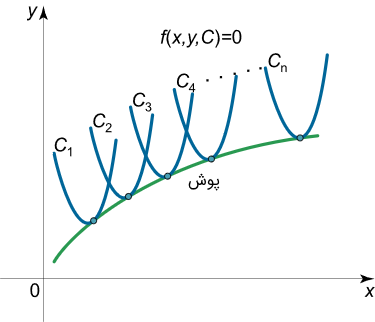
معادلات پارامتری پوش توسط دستگاه معادلات زیر تعیین می‌‌شود:

$$ \large \left \{ \begin {array} { l }
f \left ( { x , y , C } \right ) = 0 \\
{ f’ _ C } \left ( { x , y , C } \right ) = 0
\end {array} \right . , $$

این دستگاه معادلات شامل معادله اصلی دسته منحنی‌‌ها و معادله‌‌ای است که با مشتق گرفتن از معادله اصلی نسبت به پارامتر $$C$$ به دست می‌‌آید. با حذف پارامتر $$C$$ از این معادلات، می‌‌توانیم معادله پوش را به شکل صریح یا ضمنی به دست آوریم.

دستگاه معادلات فوق، شرط لازم برای وجود پوش است. علاوه بر منحنی پوش، جواب دستگاه معادلات ممکن است شامل مثلاً نقاط تکین منحنی‌‌های دسته‌‌ای باشد که متعلق به پوش نیستند. مجموعه تمام جواب‌‌های این دستگاه معادلات، منحنی مبیّن (Discriminant Curve) نامیده می‌‌شود. به طور کلی، می‌‌توان گفت که پوش قسمتی از منحنی مبیّن است.

برای یافتن معادله یکتای پوش، از شروط کافی استفاده می‌‌کنیم. فرض می‌‌شود که -علاوه بر دستگاه معادلات فوق- نامساوی‌‌های زیر برقرار باشند:

$$ \large { \left | { \begin {array} { * { 2 0 } { c } }
{ \frac { { \partial f } } { { \partial x } } } & { \frac { { \partial f } } { { \partial y } } } \\
{ \frac { { \partial { f’ _ C } } } { { \partial x } } } & { \frac { { \partial { f’ _ C } } } { { \partial y } } }
\end {array}} \right| \ne 0 , } \; \; \; \kern-0.3pt
{ \frac { { { \partial ^ 2 } f } } { { \partial { C ^ 2 } } } \ne 0 . } $$

توجه کنید که هیچ‌کدام از دسته منحنی‌‌های یک پارامتری پوش ندارند. به عنوان مثال، دسته‌‌ای از دایره‌‌های هم‌‌مرکز را در نظر بگیرید (شکل 2) که با معادله زیر نشان داده می‌‌شوند:

$$ \large { x ^ 2 } + { y ^ 2 } = { C ^ 2 } . $$

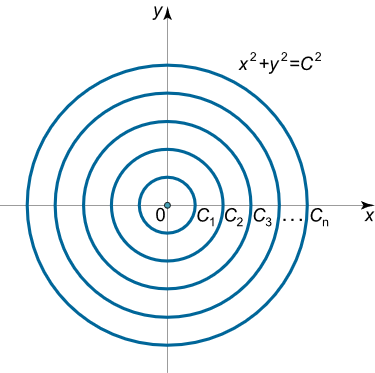
همان‌طور که مشاهده می‌‌کنیم، برای این مجموعه منحنی‌‌ها هیچ پوشی وجود ندارد.

مثال‌ها

در این بخش، مثال‌هایی از پوش دسته منحنی‌‌ها را ارائه می‌کنیم.

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

مثال ۱

پوش دسته‌‌ای از دایره‌‌ها را که با معادله زیر نشان داده می‌‌شوند، بیابید.

$$ \large { \left ( { x – C } \right ) ^ 2 } + { \left ( { y – C } \right ) ^ 2 } = 1 . $$

حل: برای به دست آوردن پوش، از دستگاه معادلات زیر استفاده می‌‌کنیم:

$$ \large \left\{ \begin {array} { l }
f \left ( { x , y , C } \right ) = 0 \\
{ f’ _ C } \left ( { x , y , C } \right ) = 0
\end {array} \right . . $$

معادله اول دسته منحنی‌‌ها را توصیف می‌‌کند و در صورت مسئله داده می‌‌شود. با مشتق گرفتن از معادله نسبت به پارامتر $$C$$، داریم:

$$ \large { 2 \left ( { x – C } \right ) \cdot \left ( { – 1 } \right ) + 2 \left ( { y – C } \right ) \cdot \left ( { – 1 } \right ) = 0 , } \; \; \\ \large \Rightarrow { x – C + y – C = 0 , } \; \; \Rightarrow { x + y – 2 C = 0 . } $$

بنابراین، دستگاه معادلات را می‌‌توان به صورت زیر نوشت:

$$ \large \left \{ \begin {array} { l }
{ \left ( { x – C } \right ) ^ 2 } + { \left ( { y – C } \right ) ^ 2 } = 1 \\
x + y – 2 C = 0
\end {array} \right . . $$

پارامتر $$C$$ را از معادله دوم به دست می‌‌آوریم و در معادله اول جایگذاری می‌‌کنیم:

$$ \large C = \frac { { x + y } } { 2 } , \; \; \Rightarrow { { \left ( { x – \frac { { x + y } } { 2 } } \right ) ^ 2 } + { \left ( { y – \frac { { x + y } } { 2 } } \right ) ^ 2 } = 1 , } \; \; \\ \large \Rightarrow { { \left ( { x – \frac { x } { 2 } – \frac { y } { 2 } } \right ) ^ 2 } + { \left ( { y – \frac { x } { 2 } – \frac { y } { 2 } } \right ) ^ 2 } = 1 , } \; \; \\ \large \Rightarrow { \frac { { 2 { { \left ( { y – x } \right ) } ^ 2 } } } { 4 } = 1 , } \; \; \Rightarrow { { \left ( { y – x } \right ) ^ 2 } = 2 , } \; \; \\ \large \Rightarrow { y – x = \pm \sqrt 2 , } \; \; \Rightarrow { y = x \pm \sqrt 2 . } $$

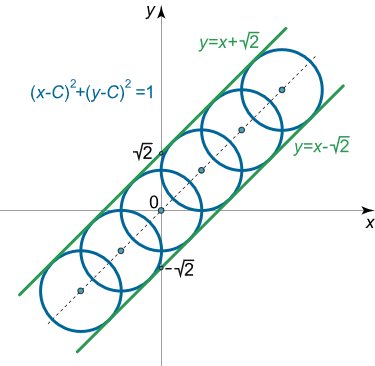
توجه کنید که این دسته دایره‌‌ها دارای نقاط تکین نیستند؛ در نتیجه، جواب حاصل، معادله پوش بوده و شامل دو خط راست است:

$$ \large y = x – \sqrt 2 \; \; \text {and} \; \; y = x + \sqrt 2 . $$

این دسته دایره‌‌ها و دو خط پوش در شکل 3 نشان داده شده‌‌اند.

مثال ۲

پوش دسته بیضی‌‌هایی با معادله زیر را در صورتی که $${a^2} + {b^2} = 1$$ باشد، به دست آورید.

$$ \large \frac { { { x ^ 2 } } } {{ { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 $$

حل: معادله این دسته منحنی‌‌ها را می‌‌توان به صورت زیر نوشت:

$$ \large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { 1 – { a ^ 2 } } } = 1 , $$

در اینجا نیم‌‌محور $$a$$ یک پارامتر و $$0 \lt a \lt 1$$ است. با مشتق گرفتن از این معادله نسبت به پارامتر $$a$$، معادله دوم به دست می‌‌آید:

$$ \large - \frac { { 2 { x ^ 2 } } } { { { a ^ 3 } } } – \frac { { { y ^ 2 } \cdot \left ( { – 2 a } \right ) } } { { { { \left ( { 1 – { a ^ 2 } } \right ) } ^ 2 } } } = 0 , \; \; \Rightarrow { – \frac { { 2 { x ^ 2 } } } { { { a ^ 3 } } } + \frac { { 2 { y ^ 2 } a } } { { { { \left ( { 1 – { a ^ 2 } } \right ) } ^ 2 } } } = 0 , } \; \; \\ \large \Rightarrow { \frac { { { y ^ 2 } a } } { { { { \left ( { 1 – { a ^ 2 } } \right ) } ^ 2 } } } = \frac { { { x ^ 2 } } } { { { a ^3 } } } , } \; \; \Rightarrow { { y ^ 2 } { a ^ 4 } = { x ^ 2 } { \left ( { 1 – { a ^ 2 } } \right ) ^ 2 } .} $$

حال از طرفین معادله حاصل جذر می‌‌گیریم:

$$ \large { { y ^ 2 } { a ^ 4 } = { x ^ 2 } { \left ( { 1 – { a ^ 2 } } \right ) ^ 2 } , } \; \; \Rightarrow { \left| y \right | { a ^ 2 } = \left | x \right | \left ( { 1 – { a ^ 2 } } \right ) . } $$

سپس، $$a^2$$ را محاسبه می‌‌کنیم:

$$ \large { \left | y \right | { a ^ 2 } = \left | x \right | – \left | x \right | { a ^ 2 } , } \; \; \Rightarrow { \left ( { \left | x \right | + \left | y \right | } \right ) { a ^ 2 } = \left | x \right| , } \; \; \Rightarrow { { a ^ 2 } = \frac { { \left | x \right | } } { { \left | x \right | + \left| y \right | } } . } $$

با قرار دادن این رابطه در معادله اول و با فرض اینکه این دسته منحنی‌‌ها هیچ نقطه تکینی ندارند، پوش دسته بیضی‌‌ها را به دست می‌‌آوریم:

$$ \large \frac { { { x ^ 2 } } } { { \frac { { \left | x \right | } } { { \left | x \right | + \left | y \right | } } } } + \frac { { { y ^ 2 } } } { { 1 – \frac { { \left | x \right | } } { { \left | x \right | + \left | y \right | } } } } = 1 , \; \Rightarrow { \frac { { { x ^ 2 } \left ( { \left | x \right | + \left | y \right | } \right ) } } { { \left | x \right | } } + \frac { { { y ^ 2 } \left ( { \left | x \right | + \left | y \right | } \right ) } } { { \left | x \right | + \left | y \right | – \left | x \right | } } = 1 , } \\ \large \Rightarrow { { \left | x \right | ^ 2 } + \left | x \right | \left | y \right | + \left | x \right | \left | y \right | + { \left | y \right | ^ 2 } = 1 , } \; \; \\ \large \Rightarrow { { \left ( { \left | x \right | + \left | y \right | } \right ) ^ 2 } = 1 , } \; \; \Rightarrow { \left | x \right | + \left | y \right | = \pm 1 . } $$

بدیهی است که ریشه منفی در اینجا معنی ندارد. بنابراین، معادله نهایی پوش به صورت زیر خواهد بود:

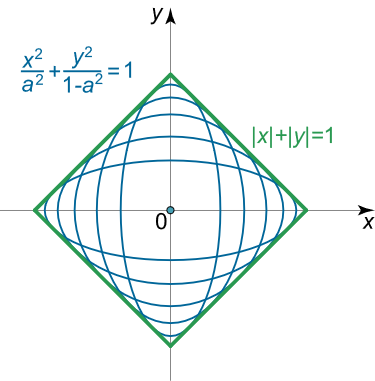
$$ \large \left | x \right | + \left | y \right | = 1 . $$

شکل حاصل از این معادله به صورت یک مربع است (شکل 4).

مثال ۳

پوش دسته خطوط راستی را بیابید که در آن ضمن اینکه پاره‌‌خط‌‌ها همدیگر را قطع می‌‌کنند، توسط محورهای مختصات نیز مثلث‌‌هایی با مساحت یکسان تشکیل می‌‌دهند.

حل: ابتدا معادله خط راستی را می‌نویسیم که با محورهای مختصات برخورد می‌‌کند:

$$ \large \frac { x } { a } + \frac { y } { b } = 1 , $$

که در آن، $$a$$ و $$b$$، به ترتیب، محل‌های برخورد با محورهای $$x$$ و $$y$$ هستند. طبق تقارن، در نظر گرفتن این خطوط در ربع اول کافی است، یعنی فرض می‌‌کنیم که $$a > 0$$ و $$b>0$$ باشد. مساحت مثلث قائم الزاویه (شکل 5) برابر است با:

$$ \large S = \frac { { a b } } { 2 } . $$

در نتیجه، $$b = \large\frac{{2S}}{a}\normalsize$$ است. پس می‌‌توان معادله دسته خطوط راست را به صورت زیر بازنویسی کرد:

$$ \large \frac { x } { a } + \frac { { a y } } { { 2 S } } = 1, $$

که در آن، پاره‌‌خط $$a$$ یک پارامتر است.

از این معادله نسبت به $$a$$ مشتق می‌‌گیریم:

$$ \large – \frac { x } { { { a ^ 2 } } } + \frac { y } { { 2 S } } = 0 $$

سپس، $$a$$ را برحسب سایر متغیرها به دست می‌‌آوریم:

$$ \large { - \frac { x } { { { a ^ 2 } } } + \frac { y } { { 2 S } } = 0 , } \; \; \Rightarrow { { a ^ 2 } y = 2 S x , } \; \; \\ \large \Rightarrow { { a ^ 2 } = \frac { { 2 S x } } { y } , } \; \; \Rightarrow { a = \sqrt { \frac { { 2 S x } } { y } } . } $$

اگر عبارت به دست آمده برای $$a$$ را در معادله اول جایگذاری کنیم، معادله پوش به دست می‌‌آید (در اینجا فرض می‌‌کنیم که این دسته خطوط راست هیچ نقطه تکینی ندارند):

$$ \large \frac { x } { a } + \frac { { a y } } { { 2 S } } = 1 , \; \; \Rightarrow { \frac { x } { { \sqrt { \frac { { 2 S x } } { y } } } } + \frac { { \sqrt { \frac { { 2 S x } } { y } } y } } { { 2 S } } = 1 , } \; \; \\ \large \Rightarrow { \frac { { \sqrt { x y } } } { { \sqrt { 2 S } } } + \frac { { \sqrt { x y } } } { { \sqrt { 2 S } } } = 1 , } \; \; \Rightarrow { 2 \sqrt { x y } = \sqrt { 2 S } , } \; \; \Rightarrow { \sqrt { x y } = \sqrt { \frac { S } { 2 } } . } $$

در ربع اول $$x>0$$ و $$y>0$$ است. در نتیجه، خواهیم داشت:

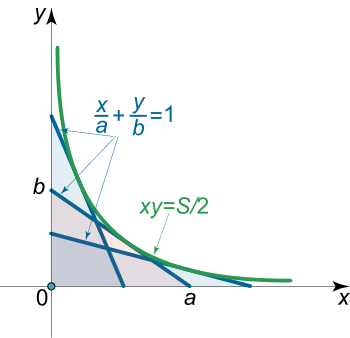
$$ \large x y = \frac { S } { 2 } . $$

همانطور که می‌‌بینیم، معادله پوش به صورت معادله یک هذلولی است.

مثال ۴

پوش دسته بیضی‌‌های زیر را که دارای مساحت یکسانی هستند، به دست آورید:

$$ \large \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { b ^ 2 } } } = 1 $$

حل: مساحت یک بیضی برابر است با:

$$ \large S = \pi a b . $$

بنابراین، معادله دسته منحنی‌‌ها را می‌‌توان به صورت زیر نوشت:

$$ \large { \frac { { { x ^ 2 } } } { { { a ^ 2 } } } + \frac { { { y ^ 2 } } } { { { { \left ( { \frac { S } { { \pi a } } } \right ) } ^ 2 } } } = 1 } $$     یا     $$ \large \frac { { { x ^ 2 } } } {{ { a ^ 2 } }} + \frac { { { \pi ^ 2 } { y ^ 2 }{ a ^ 2 } } } { { { S ^ 2 } } } = 1 $$

در اینجا نیم‌‌محور $$a$$ یک پارامتر است. اگر نسبت به $$a$$ مشتق بگیریم، معادله دیگری به دست می‌‌آید:

$$ \large - \frac { { 2 { x ^ 2 } } } { { { a ^ 3 } } } + \frac { { 2 { \pi ^ 2 } { y ^ 2 } a } } { { { S ^ 2 } }} = 0 , \; \; \Rightarrow { \frac { { { x ^ 2 } } } { { { a ^ 3 } } } = \frac { { { \pi ^ 2 } { y ^ 2 } a } } { { { S ^ 2 } } } , \; \; } \\ \large \Rightarrow { {S ^ 2 } { x ^ 2 } = { \pi ^ 2 } { y ^ 2 }{ a ^ 4 } , \; \; } \Rightarrow { S \left | x \right | = \pi \left | y \right |{ a ^ 2 } . } $$

اکنون $$a^2$$ را به دست آورده و در معادله اول جایگذاری می‌‌کنیم:

$$ \large { { a ^ 2 } = \frac { { S \left | x \right | } } { { \pi \left | y \right | } } , \; \; } \Rightarrow { \frac { { { x ^ 2 } } } { { \frac { { S \left | x \right | } } { { \pi \left | y \right | } } } } + \frac { { \frac { { { \pi ^ 2 } { y ^ 2 } S \left | x \right | } } { { \pi \left | y \right | } } } } { { { S ^ 2 } } } = 1 , \; \; } \\ \large \Rightarrow { \frac { { \pi \left | x \right | \left | y \right | } } { S } + \frac { { \pi \left | x \right | \left | y \right | } } { S } = 1 , \; \; } \Rightarrow { \frac { { 2 \pi \left | x \right | \left | y \right | } } { S } = 1 , \; \; }\\ \large \Rightarrow { 2 \pi \left | x \right | \left | y \right | = S , \; \; } \Rightarrow { \left | y \right | = \frac { S } { { 2 \pi \left | x \right | } } . } $$

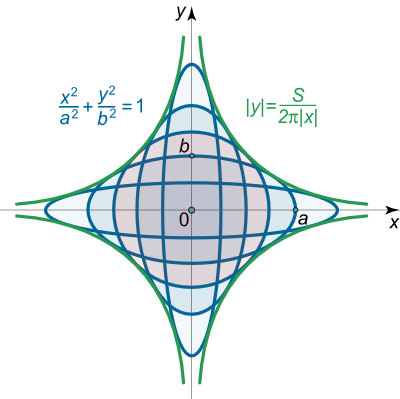
این معادله که پوش دسته بیضی‌‌های مفروض است، شامل چهار انشعاب هذلولی شکل است (شکل 6).

مثال ۵

پوش دسته خطوط راست با معادله متعارف زیر را بیابید:

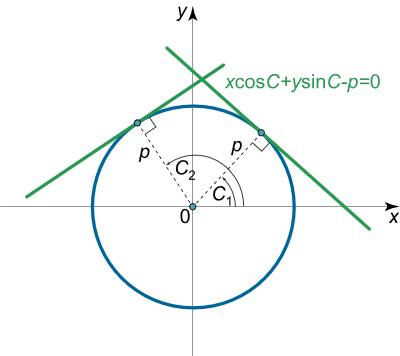
$$ \large x \cos C + y \sin C – p = 0 . $$

حل: در این معادله، $$\cos C$$ و $$\sin C$$ کسینوس‌‌های هادی بردار نرمال عمود بر خط راست هستند (شکل 7) و $$p$$ فاصله خط تا مبدأ است.

از معادله دسته خطوط راست نسبت به پارامتر $$C$$ مشتق می‌‌گیریم:

$$ \large { { \left ( { x \cos C + y \sin C – p } \right ) ^ \prime } = 0 , \; \; } \\ \large \Rightarrow { – x \sin C + y \cos C = 0 , \; \; }\\ \large \Rightarrow { x \sin C = y \cos C , \; \; } \Rightarrow { \tan C = \frac { y } { x } . } $$

$$\cos C$$ و $$\sin C$$ را برحسب $$\tan C$$ می‌‌نویسیم:

$$ \large { \cos C = \pm \frac { 1 } { { \sqrt { 1 + { { \tan } ^ 2 } C } } } , } \; \; \; \kern-0.3pt { \sin C = \pm \frac { { \tan C } } { { \sqrt { 1 + { { \tan } ^ 2 } C } } } . } $$

در نتیجه:

$$ \large { \cos C = \pm \frac { 1 } { { \sqrt { 1 + { { \left ( { \frac { y } { x } } \right ) } ^ 2 } } } } } = { \pm \frac { 1 } { { \sqrt { 1 + \frac { { { y ^ 2 } } } { { { x ^ 2 } } } } } } } = { \pm \frac { 1 } { { \sqrt { \frac { { { x ^ 2 } + { y ^ 2 } } } { { { x ^ 2 } } } } } } } = { \pm \frac { x } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } , } $$

$$ \large \sin C = \pm \frac { { \frac { y } { x } } } { { \sqrt { 1 + { { \left ( { \frac { y } { x } } \right ) } ^ 2 } } } } = { \pm \frac { { \frac { y } { x } } } { { \sqrt { 1 + \frac { { { y ^ 2 } } } {{ { x ^ 2 } } } } } } } = { \pm \frac { { \frac { y } { x } } } { { \sqrt { \frac { { { x ^ 2 } + { y ^ 2 } } } { {{ x ^ 2 } } } } } } } = { \pm \frac { y } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } . } $$

با جایگذاری این روابط در معادله دسته خطوط راست، خواهیم داشت:

$$ \large { x \cos C + y \sin C = p , \; \; } \\ \large \Rightarrow { x \left ( { \pm \frac { x } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } } \right ) + y \left ( { \pm \frac { y } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } } \right ) } = { p , \; \; }\\ \large \Rightarrow { \pm \frac { { { x ^ 2 } + { y ^ 2 } } } { { \sqrt { { x ^ 2 } + { y ^ 2 } } } } = p , \; \; } \Rightarrow { \pm \sqrt { { x ^ 2 } + { y ^ 2 } } = p , \; \; } \Rightarrow { { x ^ 2 } + { y ^ 2 } = { p ^ 2 } . } $$

بنابراین، پوش این دسته خطوط راست، دایره‌‌ای به شعاع $$p$$ است که مرکز آن در مبدأ قرار دارد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش های معادلات دیفرانسیل به همراه حل نمونه سئوالات آزمون کارشناسی ارشد
• آموزش ریاضی پایه دانشگاهی
• دستگاه معادلات دیفرانسیل خطی — به زبان ساده
• رسم تابع — با مثال های حل شده
• معادلات دیفرانسیل ضمنی — به زبان ساده

^^