پراش چیست؟ – به زبان ساده

احتمالا شکل دایره‌ای امواج آب را حول مانعی که در مسیر حرکت آن‌ قرار دارد، دیده باشید. به خمیده شدن یا گستردگی امواج در اثر برخورد با یک مانع یا در عبور از یک روزنه یا شکاف، «تفرق یا پراش» (Diffraction) می‌گویند. پس اگر بخواهیم بدانیم پراش چیست، بهترین تعریف این است که آن را پدیده‌ای بدانیم که ناشی از برهم‌کنش امواج با اجسام است و برای امواج در حال انتشار، در اثر برخورد با یک مانع یا در هنگام عبور از یک شکاف یا روزنه، رخ می‌دهد. پراش زمانی ایجاد می‌شود که طول موج جبهه موج فرودی مشابه ابعاد شکاف یا مانع باشد. میزان گستردگی امواج پراشیده شده یا اندازه پراش، به ابعاد مانع یا پهنای شکافی که در مسیر امواج فرودی قرار می‌گیرد، بستگی دارد.

در این نوشته از مجله فرادرس، ابتدا توضیح می‌دهیم که پراش چیست و روش‌های ایجاد آن از تک شکاف یا دو شکاف چه تفاوتی با هم دارند. سپس با فرمول‌های آن، تفاوت‌هایی که با پدیده‌های موجی مشابه مانند «تداخل» (Interference) دارد و انواع پراش شامل «پراش فرانهوفر» (Fraunhofer Diffraction) و «پراش فرنل» (Fresnel Diffraction) آشنا خواهید شد. در انتهای این مطلب نیز چند سوال در قالب آزمون برای شما در نظر گرفته شده است که می‌توانید با پاسخ‌دهی به آن‌ها دانش خود را در مورد مفهوم پراش محک بزنید.

پراش چیست؟

به خمیده شدن امواج پس از عبور از شکاف یا روزنه و یا در برخورد با یک مانع، تفرق یا پراش گفته می‌شود. پراش یکی از نتایج برهم‌کنش موج با ماده است. هر چه طول موج جبهه موج فرودی ($$\lambda$$) نسبت به پهنای شکاف یا ابعاد مانع ($$d$$) بزرگتر باشد ($$d\ll\lambda$$)، پراش بهتری داریم و امواج پراشیده شده نسبت به جبهه موج فرودی با زاویه بیشتری پراکنده خواهند شد. پراش دو نوع است، فرانهوفر و فرنل. در پراش فرانهوفر، فاصله پرده و شکاف ایجاد کننده پراش خیلی زیاد است، به گونه‌ای که می‌توانیم امواج پراشیده شده را به‌صورت خطوط مستقیم و موازی با هم در نظر بگیریم.

فیلم آموزش فیزیک – پایه دوازدهم در فرادرس

کلیک کنید

جدول زیر فرمول‌های پراش از تک شکاف و دو شکاف را نشان می‌دهد:

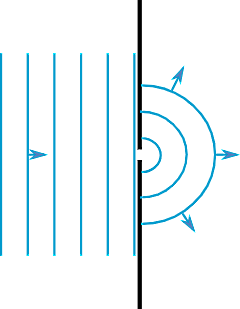
پراش برای امواج مختلف مانند نور، امواج مادون قرمز، اشعه فرابنفش، اشعه ایکس، صوت و ... رخ می‌دهد، فقط کافی است این موج از یک روزنه با ابعاد مناسب عبور کند یا با یک مانع با ابعاد مناسب مواجه شود. اگر بخواهیم پراش را به زبان ساده توضیح دهیم، موقعیتی را تصور کنید که در آن امواج در حال انتشار در مسیر خود به یک مانع برخورد می‌کنند. برهم‌کنش بین موج و مانع، باعث می‌شود شکل امواج تغییر کند، به این صورت که پیش از برخورد با مانع، امواج به‌صورت خطوطی عمودی و موازی با هم (جبهه موج فرودی) هستند، در حالی که پس از برخود با مانع، شکل امواج تغییر خواهد کرد. هر چه مانع بزرگتر باشد، شکل امواج هم نامنظم‌تر خواهد شد.

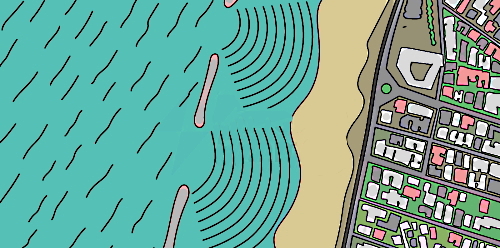
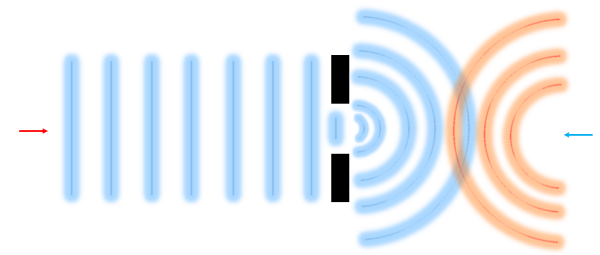
حالا اگر این امواج به‌جای برخورد با مانع، بخواهند از یک یا چند شکاف باز یا روزنه کوچک عبور کنند، باز هم چنین رفتاری را مشاهده خواهیم کرد. در این شرایط، شکل نامنظم امواج ناشی از برخود آن‌ها با لبه‌های شکاف‌ها است. همان‌طور که در تصویر زیر مشاهده می‌کنید، موجی در حال انتشار به سمت دو روزنه است و پیکان‌ قرمز افقی، جهت انتشار موج را نشان می‌دهد. موج هنگام عبور از این شکاف‌های باز، دچار پراش می‌شود و شکل آن تغییر خواهد کرد.

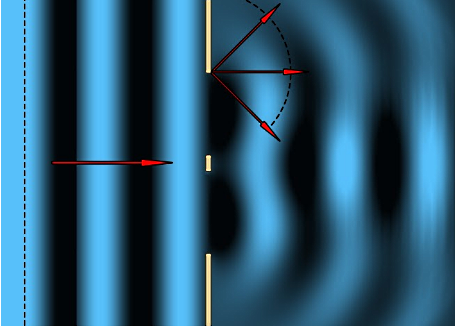
موج پراشیده شده به‌صورت خط‌چین‌های دایره‌ای در شکل بالا نمایش داده شده است. هر چقدر این موج از شکاف‌ها دورتر شود، به شکل اولیه‌ خود یعنی خط‌چین عمودی، نزدیک‌تر خواهد شد. یکی از مهم‌ترین کاربردهای پراش، روش مشخصه‌یابی مهمی به نام «پراش اشعه ایکس» (X-Ray Diffraction) یا XRD است. در این روش اشعه ایکس به یک جامد تابانده می‌شود و الگوی پراش حاصل از این تابش، نشان می‌دهد مشخصات جامد از جمله ساختار بلوری آن به چه صورت است. پس پراش به ما کمک می‌کند تا ساختار ماده را مطالعه کنیم. در این زمینه می‌توانید به مطلب «کریستالوگرافی چیست؟ — بلورشناسی و بلورنگاری به زبان ساده» از مجله فرادرس مراجعه کنید.

مدل موجی هویگنس

پیش از ارائه توضیحات بیشتر در مورد اینکه پراش چیست، بهتر است ابتدا با مدل هویگنس آشنا شویم. مدل موجی هویگنس، مقدمه‌ای برای درک انتشار امواج و در نتیجه درک پدیده پراش به‌شمار می‌رود. در قرن هفدهم، «کریستین هویگنس» (Christiaan Huygens) این ایده را مطرح کرد که می‌توانیم یک جبهه موج را به‌صورت مجموعه نقاط مجزایی در نظر بگیریم که هر کدام مانند یک منبع تولید موج عمل کرده و موجک‌های کروی ثانویه‌ای را گسیل می‌کنند.

فیلم آموزش فیزیک 3 – حل تمرین در فرادرس

کلیک کنید

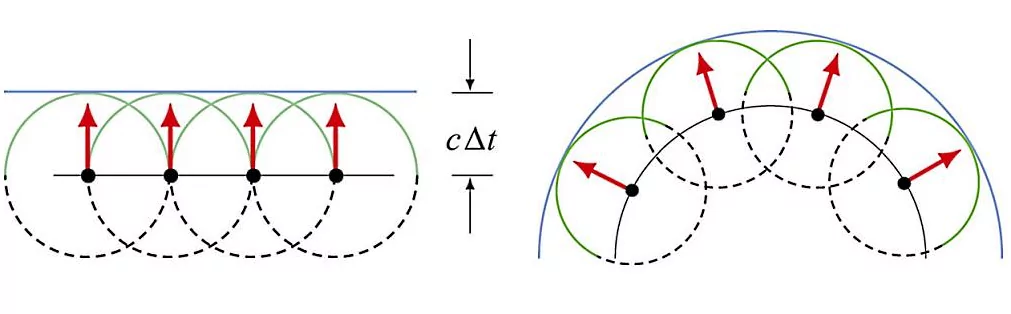
به این ترتیب، جبهه موج جدیدی حاصل خواهد شد که از اتصال تمام خطوط مماس بر موجک‌های کروی ثانویه به‌دست آمده است. شکل بالا، نحوه انتشار امواج را بر مبنای اصل هویگنس نشان می‌دهد. سرعت انتشار امواج در این شکل برابر با سرعت نور یا $$c$$ است. در شکل سمت راست جبهه موج جدید شکل کروی دارد، در حالی که در تصویر سمت چپ جبهه موج جدید یک خط افقی شده است.

بنابراین زمانی که موجی از شکافی عبور می‌کند، برخی از این موجک‌ها با هم تداخل کرده و با از بین بردن یکدیگر، مانع عبور موج خواهند شد. از طرفی بر اثر تداخل برخی موجک‌ها و تقویت یکدیگر، موجک‌های تازه‌ای ایجاد می‌شوند که می‌توانند از روزنه عبور کنند و در نتیجه پراش خواهیم داشت. پراش را می‌توان از چند منظر بررسی کرد، اینکه پراش چطور ایجاد شده است (در برخورد با مانع یا هنگام عبور از یک یا دو شکاف) یا اینکه چه انواعی دارد. در بخش‌های بعد، هر کدام از این موارد را توضیح خواهیم داد.

چگونه ویژگی‌های امواج را با فرادرس بهتر یاد بگیریم؟

مبحث «نوسان و موج» یکی از مهم‌ترین مباحث مطرح شده در کتاب درسی فیزیک پایه دوازدهم برای رشته‌های علوم ریاضی و علوم تجربی است که شامل موضوعاتی مانند معرفی انواع موج، بازتاب، شکست، پراش و تداخل می‌شود. اگر تمایل دارید در این زمینه اطلاعات بیشتری به‌دست آورید و یا به حل تمرین‌های متنوع و تست‌‌های کنکور در این زمینه بپردازید، پیشنهاد می‌کنیم دوره‌های آموزشی زیر از مجموعه فرادرس را مشاهده کنید:

1. فیلم آموزش فیزیک دوازدهم فرادرس
2. فیلم آموزش فیزیک دوازدهم – مرور و حل تمرین فرادرس
3. فیلم آموزش فیزیک دوازدهم – نکته و حل تست کنکور فرادرس

عوامل موثر روی پراش چیست؟

پس از اینکه یاد گرفتید تعریف پراش چیست، در این بخش به توضیح سه عامل مهم و موثر در شکل‌گیری پراش می‌پردازیم که عبارت‌اند از:

• دامنه جبهه موج فرودی
• پهنای شکاف یا ابعاد مانع
• طول موج جبهه موج فرودی

برای آشنایی بیشتر با مفهوم جنبه‌های مختلف موج مانند دامنه، طول موج، سرعت و ...، پیشنهاد می‌کنیم فیلم آموزشی فیزیک پایه ۳ فرادرس را مشاهده کنید که لینک آن در ادامه برای شما قرار داده شده است:

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

برای اینکه پراش داشته باشیم، باید دامنه موج فرودی از پهنای شکاف یا ابعاد مانع بزرگتر باشد. پس اگر دامنه موج از این ابعاد خیلی کمتر باشد، پراشی نخواهیم داشت. برای مثال در شکل زیر مشاهده می‌کنید که دامنه جبهه موج فرودی با رنگ قرمز (امواج مادون قرمز) یا $$A_2$$ از دامنه جبهه موج فرودی با رنگ آبی (امواج فرابنفش) یا $$A_1$$ بزرگتر است. در نتیجه امواج مادون قرمز در عبور از شکافی با پهنای $$d$$ به اندازه زاویه $$\theta$$ پراشیده می‌شوند، در حالی که برای امواج فرابنفش پراش رخ نمی‌دهد، چون اندازه $$A_1$$ از پهنای شکاف کمتر است.

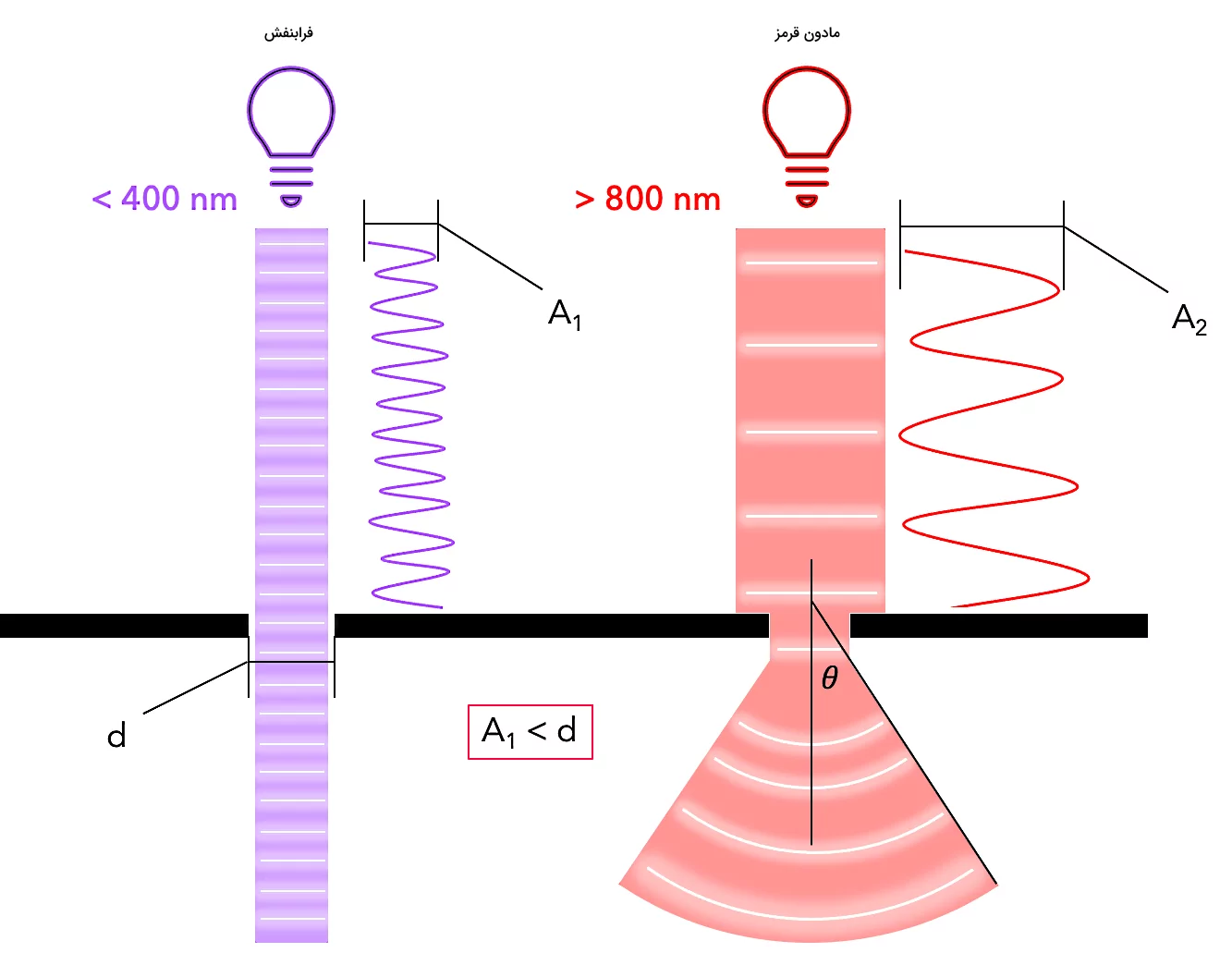
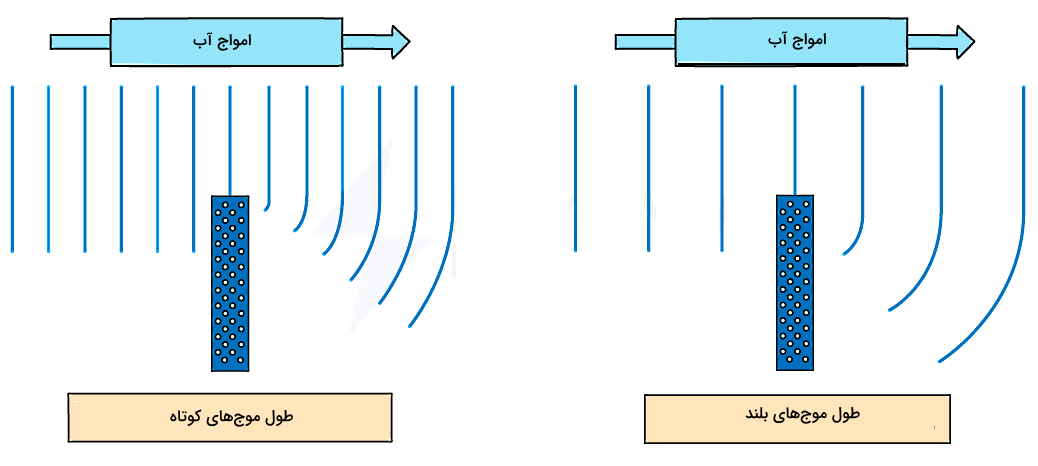
نکته دیگر این است که همواره با کاهش پهنای شکاف، پراش بیشتری خواهیم داشت و زاویه‌ای که تحت آن موج‌ها از شکاف گسترده می‌شوند نیز افزایش خواهد یافت. از طرفی اگر جبهه موج فرودی دارای طول موج کوتاهی (معادل فرکانس بالا) باشد، اثری مشابه با افزایش پهنای شکاف خواهیم داشت. به‌عبارت دیگر، با کاهش طول موج، زاویه پراش نیز کاهش خواهد یافت. این اثر را می‌توانید در تصویر زیر مشاهده کنید که در آن زاویه $$\theta_1$$ نسبت به زاویه $$\theta_2$$ کمتر است و نشان می‌دهد با در نظر گرفتن پهنای شکاف و دامنه یکسان، امواج فرابنفش نسبت به امواج مادون قرمز پراش ضعیف‌تری دارند.

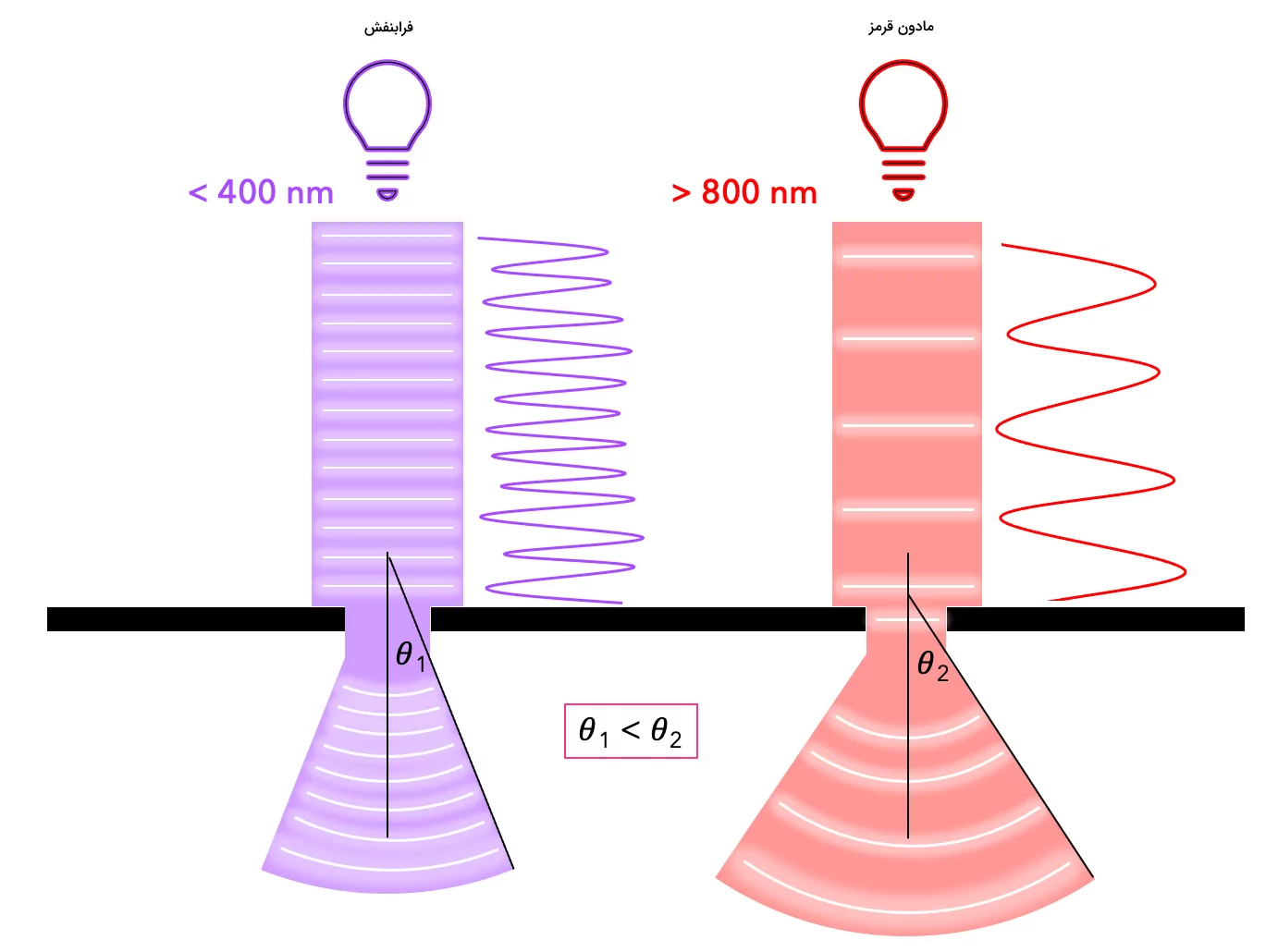
در این شکل برخلاف شکل قبل، از امواج فرابنفشی با دامنه مناسب استفاده شده تا پراش داشته باشیم. در شکل بالا دامنه هر دو جبهه موج تقریبا با هم مشابه است، اما عاملی که باعث می‌شود پراش امواج مادون قرمز بیشتر باشد، طول موج این امواج است. در مورد امواج فرابنفش به‌علت طول موج کمتر، می‌بینیم که پراش داریم، اما امواج پراشیده در زاویه‌های کمتری نسبت به امواج مادون قرمز پراشیده شده‌اند.

تفاوت تداخل و پراش چیست؟

اینکه تفاوت دو پدیده تداخل و پراش چیست، یکی از مهم‌ترین مباحثی است که در مورد پراش مطرح می‌شود و پیش از پرداختن به موضوع انواع پراش و محاسبه فرمول آن، لازم است به آن مسلط باشید. برهم‌کنش امواج پراشیده شده با یکدیگر ممکن است منجر به تشکیل الگوهای تداخلی شود. پس مهم‌ترین تفاوت تداخل و پراش در این است که در پراش، جبهه موج فرودی با یک یا چند جسم خارجی مانند مانع یا لبه‌های شکاف برهم‌کنش دارد، اما در تداخل امواجی که پراشیده شده‌اند با هم برهم‌کنش دارند و مسئله جسم خارجی مطرح نیست.

فیلم آموزش فیزیک 3 – حل تمرین در فرادرس

کلیک کنید

شکل زیر الگوی تداخلی ناشی از امواج پراشیده شده از یک دو شکافی را نمایش می‌دهد. این شکل نمونه‌ای از پراش فرانهوفر نیز به‌شمار می‌رود که در ادامه با مفهوم آن آشنا خواهید شد. در این تصویر، نور حاصل از منبعی مانند لامپ، در عبور از دو شکافی دچار پراش می‌شود. می‌دانیم نور یک موج الکترومغناطیس محسوب می‌شود، پس ماهیت موج‌گونه دارد و ممکن است پراشیده شود. سپس بین امواج پراشیده شده تداخلی صورت می‌گیرد که منجر به تشکیل یک الگوی تاریک و روشن روی پرده خواهد شد و به آن، الگوی تداخلی می‌گوییم.

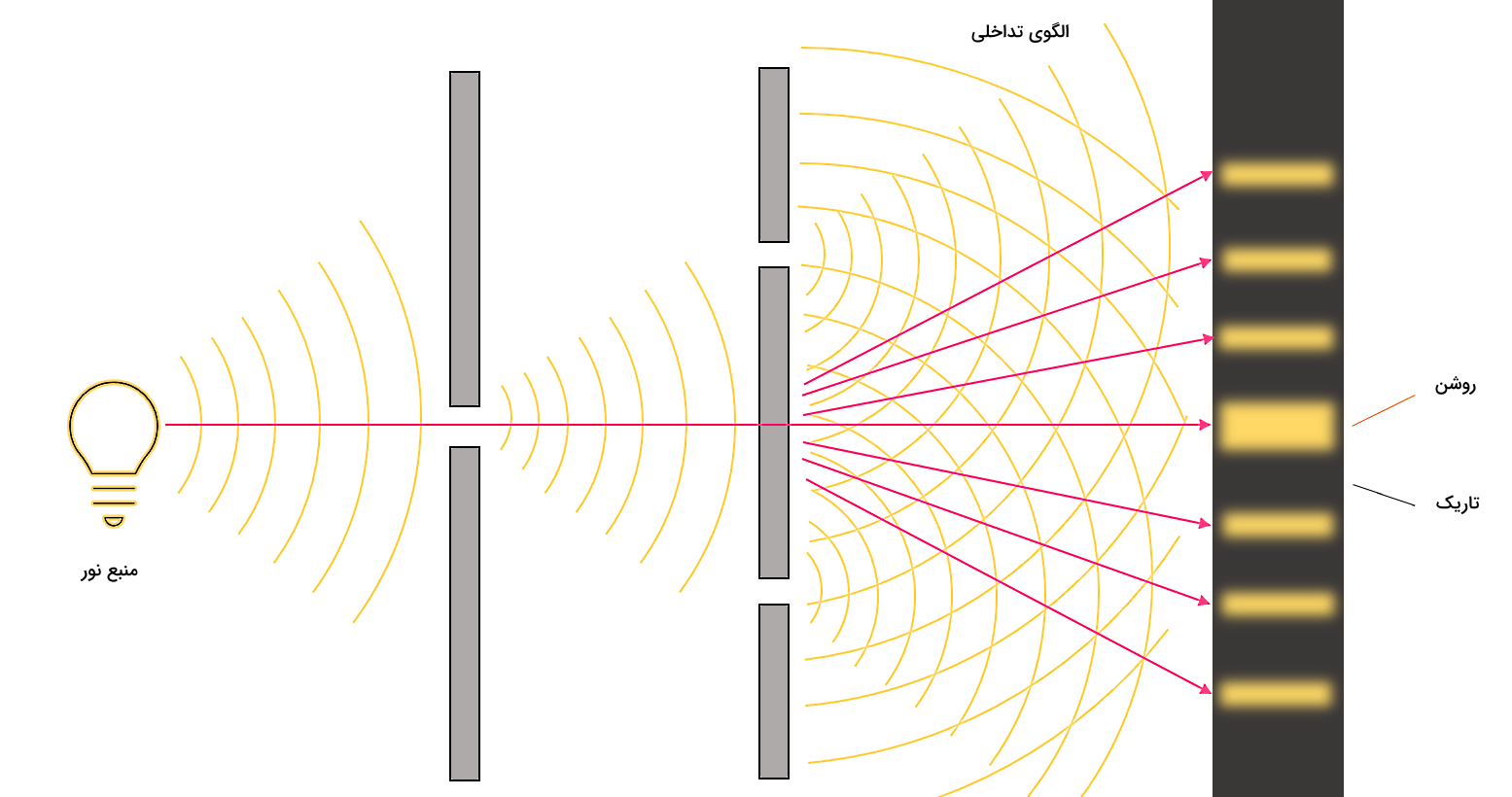
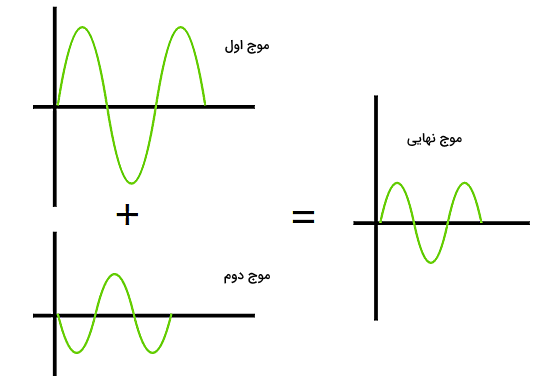
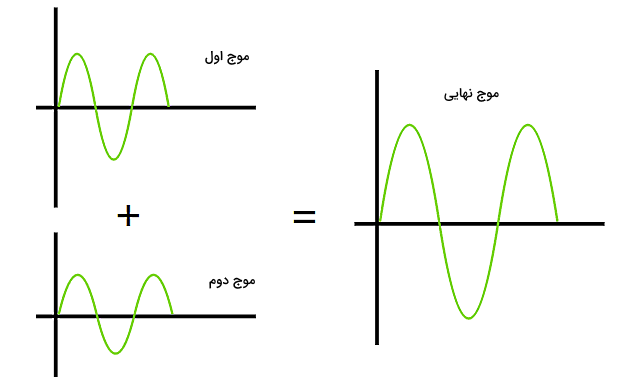
پس در این شکل علاوه بر پراش، تداخل هم داریم. برای درک بهتر تداخل امواج پراشیده شده و در نتیجه درک بهتر الگوی پراش، بهتر است به «اصل بر هم‌‌نهی امواج» (Superposition of Waves) نیز در اینجا اشاره کنیم. ناحیه‌ای را در نظر بگیرید که در آن دو موج هم‌زمان در حال انتشار هستند. طبق اصل بر هم‌نهی، جابجایی برآیند از جمع برداری جابجایی هر یک از این دو موج حاصل می‌شود. ایده بر هم‌نهی امواج را می‌توانید با نگاه کردن به تصویر زیر بهتر درک کنید. بر هم‌نهی ممکن است به دو شکل انجام شود که نتیجه آن، تداخل سازنده یا ویرانگر است.

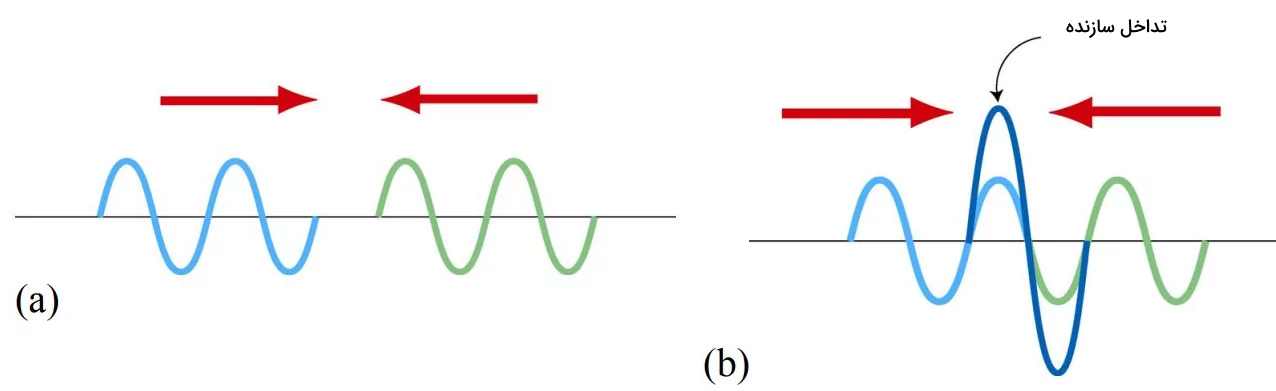
پس تداخل امواج همواره به یکی از دو شکل زیر انجام می‌شود:

• تداخل سازنده
• تداخل ویرانگر

در تداخل سازنده برهم‌کنش امواج با هم سازنده است، به این معنا که دامنه دو موج با هم جمع شده و در نتیجه، موجی با دامنه بزرگتر از دامنه امواج اولیه ایجاد خواهد شد. نشانه صورت گرفتن تداخل سازنده، ایجاد نقاط یا لکه‌های روشن روی پرده در الگوی تداخلی است. اما در تداخل ویرانگر، برهم‌کنش امواج به‌گونه‌ای است که مجموع دامنه دو موج صفر شده و حاصل آن، ایجاد نقاط یا لکه‌های تاریک روی پرده است.

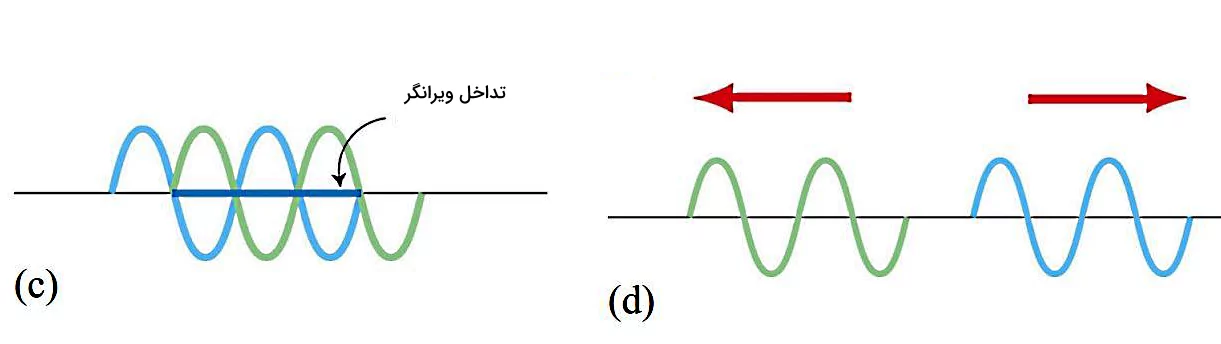
برای اینکه هر کدام از این دو نوع تداخل صورت بگیرد، لازم است دو شرط برقرار باشد:

1. منبع تولید امواج یا نور باید «همدوس» (Coherent) باشد.
2. منبع تولید امواج یا نور باید «تک‌فام» (Monochromatic) باشد.

منظور ما از همدوسی منبع نور این است که برای مثال، اگر دو موج با اختلاف فاز مشخصی تولید می‌شوند، باید این اختلاف فاز در گذر زمان تغییر نکند و ثابت باقی بماند. همچنین تک‌فام بودن منبع نور به این مفهوم است که نور تولید شده باید فقط شامل یک طول موج باشد. برای نمونه، نوری که توسط یک لامپ حبابی تولید می‌شود، همدوس محسوب نمی‌شود.

پراش از تک شکاف

در این بخش می‌خواهیم ببینیم مهم‌ترین روش‌ و شرط ایجاد پراش چیست. پراش از تک شکاف زمانی رخ می‌دهد که یک جبهه موج در عبور از یک روزنه یا شکاف، طوری گسترده شود که الگوی منحنی شکلی به‌‌صورت زیر برای آن ایجاد شود. برای رسم شماتیکی از این نوع پراش، جبهه موج فرودی را با خطوط عمودی نمایش می‌دهیم، در حالی که موج پراشیده به شکل منحنی‌های دایره‌ای شکل است.

فیلم آموزش اپتیک یا نورشناسی Optique در فرادرس

کلیک کنید

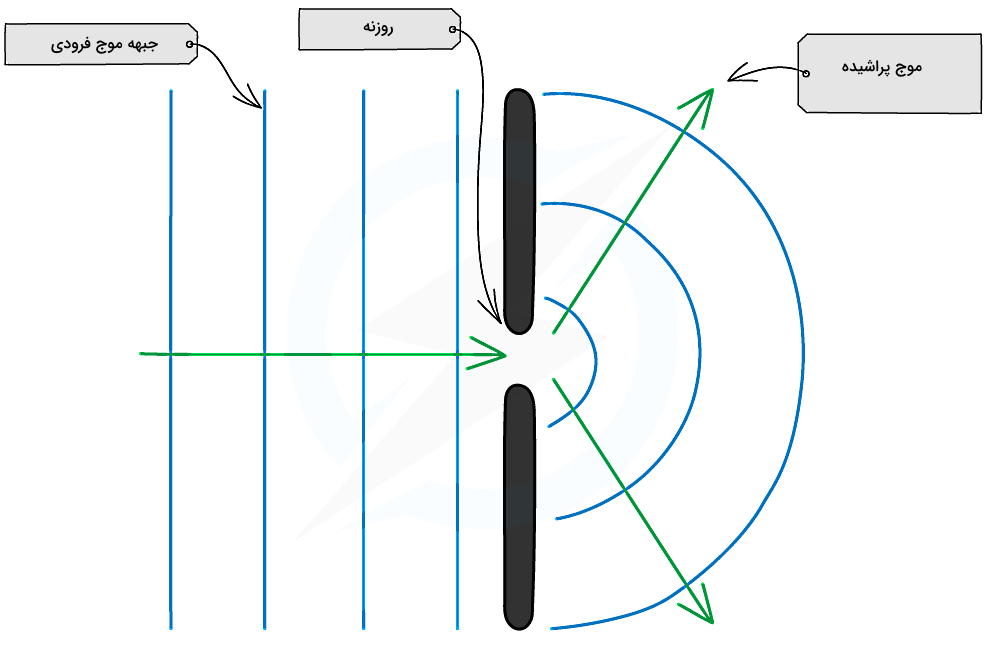
دقت کنید موج جدید دامنه کمتری نسبت به موج اولیه دارد، به این علت که لبه‌های دو سمت روزنه بخشی از انرژی موج اولیه را جذب می‌کنند. پس موج جدید دارای انرژی و در نتیجه، دامنه کمتری خواهد بود. همیشه بخشی از موج در برخورد با موانع یا لبه‌های شکاف جذب می‌شود، اما ممکن است برای بخشی از موج پراش هم داشته باشیم. برای داشتن پراش از یک تک شکاف، باید یک شرط مهم برقرار باشد که در ادامه راجع‌به آن صحبت خواهیم کرد. همچنین در بخش‌های بعد در مورد تفاوت پراش از تک شکاف با پراش از دو شکاف توضیح می‌دهیم.

فرمول پراش (شرط پراش) از تک شکاف

اگر جبهه موجی که از روزنه یا شکاف عبور می‌کند، دارای طول موج خیلی نزدیک به پهنای شکاف باشد، در این صورت پراش خواهیم داشت. این توضیح به این معنا است که اگر طول موج از پهنای شکاف کمی بیشتر باشد، پراش بیشتری برای موج اتفاق خواهد افتاد و موج با عبور از این روزنه، بیشتر گسترده خواهد شد. اما اگر طول موج از پهنا کمی کمتر باشد، پراش کمتری خواهیم داشت و گستردگی کمتری در موج خارج شده از روزنه مشاهده می‌کنیم.

پس باید دقت کنید، لازم است مقادیر طول موج و پهنا در این توضیحات به هم نزدیک باشند تا پراش داشته باشیم و ابعاد شکاف روی برهم‌کنش آن با موج تاثیرگذار است. در مورد روزنه‌هایی که خیلی خیلی از طول موج تابیده شده به روزنه کوچکتر باشند، موج عبور می‌کند، بدون اینکه دچار پراش شود. به همین ترتیب، برای شکاف‌هایی با پهنای خیلی بیشتری نسبت به طول موج، بخش زیادی از موج بدون اینکه دچار پراش شود، مستقیما از روزنه عبور خواهد کرد.

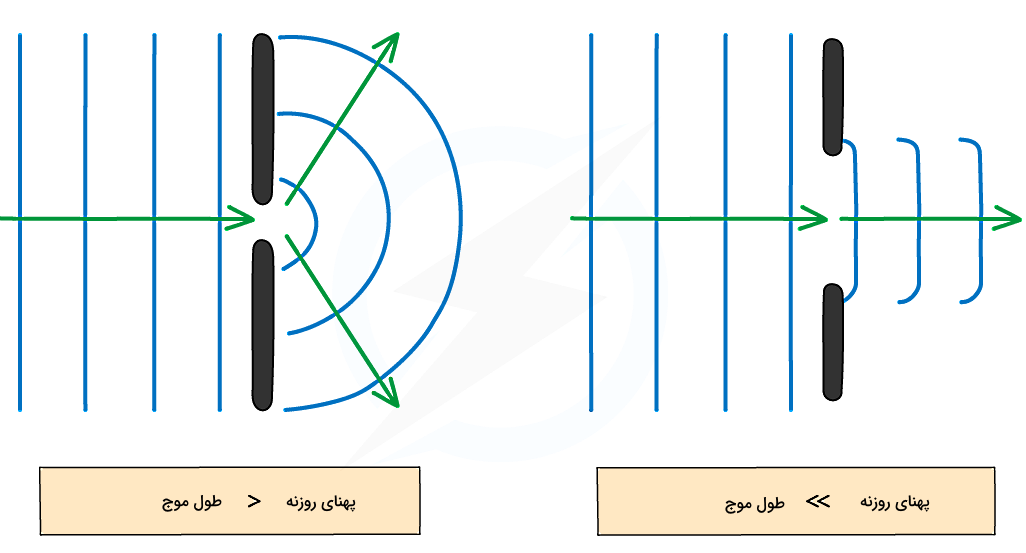
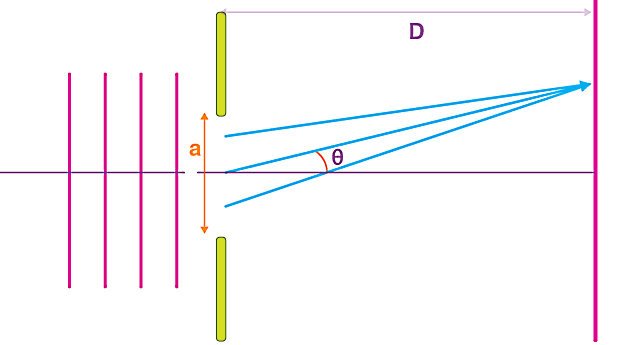
شکل بالا نشان می‌دهد اثر پهنای شکاف روی الگوی پراش چیست. در ادامه توضیح می‌دهیم که چگونه می‌توان این رابطه یا شرط را در قالب یک فرمول ریاضی نشان داد. فرض کنید اندازه شکاف را برابر با $$a$$ و طول موج جبهه موج فرودی که از یک منبع تک‌فام حاصل شده را برابر با $$\lambda$$ در نظر گرفته‌ایم. همچنین طبق شکل زیر، فاصله شکاف با پرده را با $$D$$ نشان می‌دهیم. دقت کنید برای اینکه به فرمول پراش از تک شکاف برسیم، لازم است فرض زیر را در نظر داشته باشیم:

$$a\ll D$$

یعنی باید ابعاد پهنای شکاف ما نسبت به فاصله آن از پرده خیلی خیلی زیاد باشد. از طرفی می‌توانیم مکان هر نقطه‌ روی پرده را با یک زاویه به‌صورت $$\theta$$ نشان دهیم. این زاویه را نسبت به مرکز شکاف و یکی از دو لبه آن اندازه‌گیری می‌کنیم، در حالی که می‌دانیم فاصله مرکز شکاف از هر یک از دو لبه آن برابر است با $$\frac{a}{2}$$. طبق اصل هویگنس، هر یک از این دو بخش از شکاف مانند یک منبع موج عمل می‌کند. حالا می‌خواهیم ببینیم چگونه می‌توان پراشی که از این تک شکاف اتفاق می‌افتد را با ریاضیات توصیف کرد.

در ادامه محاسبات، لازم است دو حالت برای پراش در نظر بگیریم که به تداخل امواج مربوط می‌شود. در بخش تداخل، گفتیم که امواج پراشیده شده ممکن است با هم تداخل سازنده یا ویرانگر داشته باشند. نتیجه تداخل سازنده ایجاد لکه‌های روشن است، در حالی که برای تداخل ویرانگر، لکه‌‌های تیره روی پرده مشاهده می‌شوند.

فرمول پراش از تک شکاف در تداخل ویرانگر

در اولین بخش با در نظر گرفتن تداخل وایرنگر، می‌خواهیم ببینیم فرمول پراش چیست. فرض کنید از شکافی یک جفت پرتو موازی هم ساطع یا پراشیده می‌شوند. اگر اختلاف راه بین این دو پرتو را با $$\triangle L$$ نشان دهیم و با در نظر گرفتن یکی از دو مثلث قائم‌الزاویه در شکل زیر، می‌توانیم برای سینسوس زاویه $$\theta$$ رابطه‌ زیر را بنویسیم:

$$sin\theta=\frac{\triangle L}{\frac{a}{2}}$$

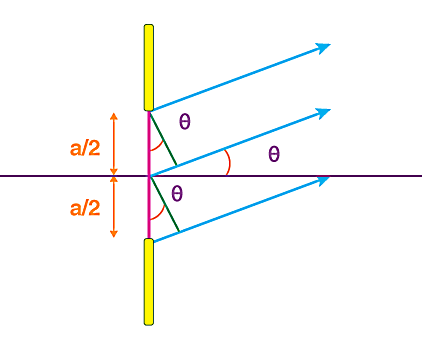
می‌دانیم در یک مثلث قائم‌الزوایه، سینوس زاویه‌ای مانند $$\theta$$ برابر است با نسبت اندازه ضلع مقابل به زاویه به اندازه وتر در مثلث. در هر کدام از دو مثلث بالا، وتر برابر است با $$\frac{a}{2}$$، در حالی که ضلع روبرو به زاویه $$\theta$$ همان اختلاف راه است. بنابراین اختلاف راه یا اختلاف مسیر این دو پرتو برابر می‌شود با:

$$\triangle L=\frac{a}{2}sin\theta$$

بار دیگر تاکید می‌کنیم این محاسبه فقط زمانی معتبر است که فاصله $$D$$ در مقایسه با $$a$$ خیلی بزرگ باشد. در این محاسبه می‌توانیم هر دو پرتوی فرضی موازی با هم که در فاصله $$\frac{a}{2}$$ از هم قرار دارند را در نظر بگیریم. حالا اگر بخواهیم بخش تاریک الگوی تداخلی روی پرده نمایش داده شود، اختلاف مسیر این دو پرتو باید یک تداخل ویرانگر به ما بدهد.

برای داشتن تداخل ویرانگر کافی است این اختلاف مسیر به اندازه $$\frac{\lambda}{2}$$ از فاز بیشتر شود، یعنی داشته باشیم:

$$\triangle L=\frac{\lambda}{2}$$

$$\Rightarrow \frac{\lambda}{2}=\frac{a}{2}sin\theta$$

$$\lambda=asin\theta$$

فرمول بالا برای اولین حلقه سیاه تشکیل شده روی پرده برقرار است. این رابطه به این معنا است که برای هر پرتوی که از هر نقطه از شکاف ساطع می‌شود، همواره پرتوی دیگری در فاصله $$\frac{a}{2}$$ وجود دارند که می‌توانند با هم یک تداخل ویرانگر ایجاد کنند.

برای مشخص شدن وضعیت حلقه‌ سیاه بعدی، کافی است پهنای شکاف را به چهار قسمت مساوی تقسیم کنیم که هر کدام طولی برابر با $$\frac{a}{4}$$ دارند. در این حالت مثلث تشکیل شده نسبت به مثلث قبلی کوچکتر است. اگر روند بالا را مجددا اعمال کنیم، خواهیم داشت:

$$\triangle L=\frac{a}{4}sin\theta$$

$$\triangle L=\frac{\lambda}{2}$$

$$\Rightarrow \frac{\lambda}{2}=\frac{a}{4}sin\theta$$

$$2 \lambda=asin\theta$$

با ادامه این روند و تقسیم پهنای شکاف به $$2n$$ بخش مساوی، به رابطه زیر برای تداخل ویرانگر امواج پراشیده شده می‌رسیم:

$$n \lambda=asin\theta$$

• $$n$$: عدد صحیح و مخالف صفر به صورت $$\pm1, \pm2, ...$$
• $$\lambda$$: طول موج جبهه موج فرودی
• $$a$$: پهنای شکاف
• $$\theta$$: زاویه پراش

همان‌طور که نوشته شده است، در استفاده از این فرمول باید $$n$$ مخالف صفر باشد. چون در $$n=0$$ بیشترین شدت را برای موج پراشیده شده داریم که منطبق با فرض ما در مورد ویرانگر بودن تداخل امواج نیست. هدف ما از کاربرد این فرمول، پیدا کردن مکان کمترین شدت‌‌های ایجاد شده برای امواج است.

حالا می‌خواهیم ببینیم مکان کمینه اول روی پرده دقیقا کجا قرار می‌گیرد. اگر این نقطه در فاصله $$y$$ از خط افقی $$D$$ قرار بگیرد، در این صورت برای مثلث بزرگ تشکیل شده بین $$y$$ و $$D$$ و زاویه $$\theta$$، می‌توانیم رابطه زیر را بنویسیم:

$$tan\theta=\frac{y}{D}$$

می‌دانیم تانژانت زاویه‌ای مانند $$\theta$$ در یک مثلث قائم‌الزاویه برابر است با نسبت اندازه ضلع روبرو به این زاویه به ضلع مجاور به زاویه. از طرفی برای $$\theta$$های خیلی کوچک می‌توانیم دو رابطه زیر را داشته باشیم:

$$sin\theta\approx\theta$$

$$tan\theta\approx\theta$$

با کاربرد این تقریب خواهیم داشت:

$$\Rightarrow \theta =\frac{y}{D}=\frac{\lambda}{a}$$

$$\Rightarrow y= \frac{\lambda D}{a}$$

فرمول پراش از تک شکاف در تداخل سازنده

در بخش گذشته یاد گرفتیم که اگر امواج پراشیده شده با هم تداخل ویرانگر داشته باشند، فرمول مکان قرارگیری کمترین شدت‌‌ها پس از پراش چیست. در تداخل سازنده دو موج، دامنه هر کدام از امواج با دیگری جمع می‌شود و در نتیجه موج نهایی دارای دامنه بیشتری خواهد بود.

با روندی مشابه، می‌توانیم برای تداخل سازنده امواج به فرمول زیر دست پیدا کنیم:

$$(2n+1) (\frac{\lambda}{2})=asin\theta$$

• $$n$$: عدد صحیح و مخالف صفر به صورت $$\pm1, \pm2, ...$$
• $$\lambda$$: طول موج جبهه موج فرودی
• $$a$$: پهنای شکاف
• $$\theta$$: زاویه پراش

پراش از مانع

در بخش‌های قبل آموختیم روش متداول ایجاد پراش چیست. در این بخش نوع دیگری از پراش را بررسی می‌کنیم که در آن موج فرودی قرار نیست از روزنه یا شکافی عبور کند، بلکه با یک مانع یا لبه برخورد می‌کند. در این شرایط هم پراش موج باعث گستردگی آن خواهد شد و این گستردگی به ‌گونه‌ای است که امواج پراشیده شده فضای خالی اطراف لبه یا مانع را نیز پر می‌کنند.

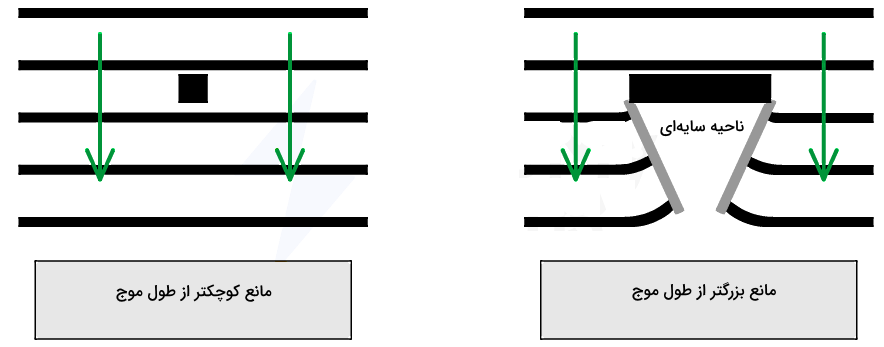
در این نوع پراش هم میزان موج‌های پراشیده بر اساس طول موج موج فرودی تعیین می‌شود، به این صورت که هر چه طول موج بزرگتری داشته باشیم، پراش هم بیشتر است. اما برای اینکه بتوانیم الگوی پراش ایجاد شده در این بخش را دقیق‌تر تحلیل کنیم، سه حالت زیر را در نظر می‌گیریم:

1. اگر ابعاد مانع نسبت به طول موج موج فرودی خیلی زیاد باشد.
2. اگر ابعاد مانع و طول موج موج فرودی هم‌اندازه باشند.
3. اگر ابعاد مانع نسبت به طول موج موج فرودی خیلی کم باشد.

در حالت اول، پراش کمی اطراف مانع ایجاد می‌شود و بیشتر موج فرودی به سمت منبع منعکس خواهند شد. همچنین یک ناحیه‌ سایه‌ای بزرگ پشت مانع ایجاد می‌شود که در آن هیچ اثری از امواج نیست. در حالت دوم، پراش حول مانع بیشتر است و ناحیه سایه‌ای شکل پشت مانع نسبت به حالت قبل، کوچکتر است. در سومین حالت، هیچ پراشی حول مانع نخواهیم داشت و تقریبا هیچ سایه‌ای تشکیل نمی‌شود.

پراش از دو شکافی

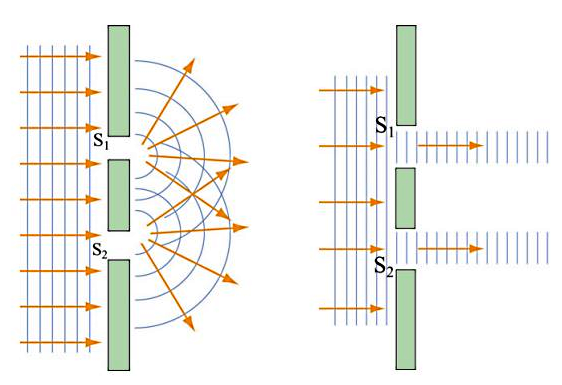
در بخش‌های قبل متوجه شدید که در مواجهه با یک تک شکاف یا مانع، پراش چیست و چگونه ایجاد می‌شود. در این بخش مسئله پراش از دو شکافی را بررسی می‌کنیم. طبق اصل هویگنس، اگر امواج نور به یک دو شکافی برسند، گسترده یا خمیده خواهند شد و الگوی پراشی به شکل زیر نشان می‌دهند. اما چنانچه هیچ گونه خمیدگی در نور ایجاد نشود و امواج نوری به همان شکلی که به دو شکافی رسیده بودند، در قالب خطوط مستقیم از آن خارج شوند، در این صورت می‌گوییم هیچ پراشی اتفاق نیفتاده است.

آزمایش دو شکافی یانگ

در آزمایش معروفی به نام «آزمایش دو شکافی یانگ» (Young’s Double-slit Experiment)، دو شکاف در مسیر جبهه موج فرودی قرار می‌گیرند. پس تا اینجا می‌توانیم بگوییم پراش از دو شکافی شبیه آزمایش دو شکافی یانگ است. در این آزمایش آن‌قدر پهنای هر کدام از شکاف‌ها کوچک است که در عمل مانند دو منبع نقطه‌ای برای تولید موج عمل می‌کنند. این آزمایش که بیشتر برای نشان دادن طبیعت موجی نور بکار می‌رود، شماتیکی به‌صورت زیر دارد:

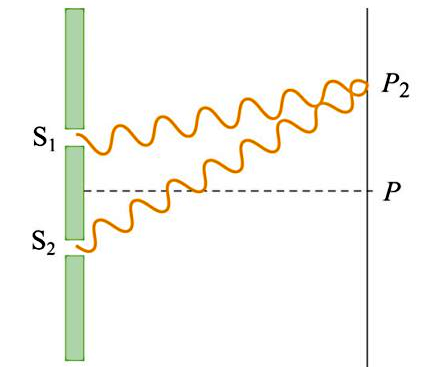
«توماس یانگ» (Thomas Young) در این آزمایش از یک منبع نور تک‌فام استفاده کرد تا امواج نور به سمت اولین شکاف $$S_0$$ ساطع شوند. نور پراشیده شده از این شکاف، به دو شکاف بعدی می‌رسد و پراش مجدد از این دو شکاف منجر به تشکیل الگوی تداخلی رو پرده سیاه خواهد شد. دو شکاف آزمایش یانگ مانند دو منبع نور همدوس عمل می‌کنند. شکل زیر نشان می‌دهد که چگونه ممکن است تداخل سازنده یا ویرانگر برای نورهای ساطع شده از این دو شکاف ایجاد شود:

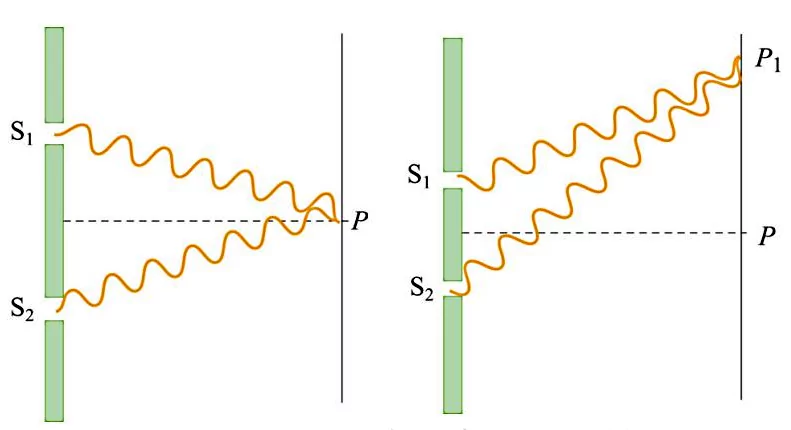
اگر دو موج پراشیده شده از دو شکافی که به یک نقطه‌ فرضی روی پرده مانند $$P$$ یا $$P_1$$ رسیده‌اند، یکدیگر را تقویت کنند، در این صورت تداخل سازنده داریم. اما اگر فاز دو موج به شکل زیر باشد، در نقطه‌ای مانند $$P_2$$ تداخل ویرانگر داریم و دو موج اثر هم را از بین می‌برند.

فرمول پراش در آزمایش دو شکافی یانگ

پس از توضیحات بالا و با در نظر گرفتن هندسه زیر برای دو شکافی یانگ، می‌توانیم محاسبه کنیم که در این حالت، فرمول پراش چیست. فرض کنید دو پرتو نور روی پرده در نقطه‌ای به نام $$P$$ به هم می‌رسند که در فاصله $$y$$ از نقطه $$O$$ قرار دارد. همچنین فاصله شکاف تا پرده را برای محاسبه فرمول پراش در این بخش $$L$$ در نظر بگیرید. همان‌طور که گفتیم، در آزمایش دو شکافی یانگ پهنای شکاف‌ها ناچیز در نظر گرفته می‌شود. در نتیجه، در محاسبات ابعاد شکاف‌ها لحاظ نخواهند شد. اما فاصله بین دو شکافی یعنی $$d$$ مهم است.

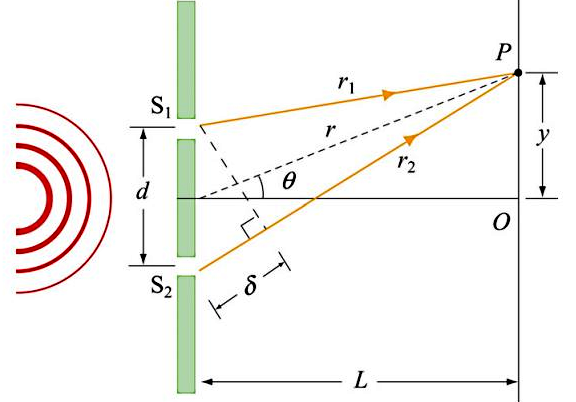
نکته مهمی که در تصویر بالا مشهود است، فاصله اضافه‌تری است که پرتو نور حاصل از شکاف دوم در مقایسه با اولی طی می‌کند. این فاصله با $$\delta$$ نشان داده شده است و برابر است با:

این فاصله معادل همان اختلاف راه یا اختلاف مسیری است که در محاسبه فرمول پراش از تک شکاف هم وجود داشت. حالا اگر برای دو مثلث بالا قانون کسینوس‌ها را بنویسیم، خواهیم داشت:

$$r_1^2=r^2+(\frac{d}{2})^2-drcos(\frac{\pi}{2}-\theta)=r^2+(\frac{d}{2})^2-drsin\theta$$

$$r_2^2=r^2+(\frac{d}{2})^2-drcos(\frac{\pi}{2}+\theta)=r^2+(\frac{d}{2})^2+drsin\theta$$

دقت کنید یکی از مثلث‌ها از سه ضلع $$r_1$$ و $$\frac{d}{2}$$ و $$r$$ ساخته شده است، در حالی که دیگری دارای سه ضلع $$r_2$$ و $$\frac{d}{2}$$ و $$r$$ است. با کم کردن دو رابطه بالا از هم و با این فرض که مانند پراش از تک شکاف همواره $$d\ll L$$ است، می‌توانیم به فرمول زیر برای اختلاف راه نور پراشیده شده در آزمایش دو شکافی برسیم:

$$\Rightarrow r_2^2-r_1^2=(r_2+r_1)(r_2-r_1)=2drsin\theta$$

$$r_1+r_2\approx2r$$

$$\Rightarrow \delta=r_2-r_1\approx dsin\theta$$

در واقع با فرض $$d\ll L$$، می‌توانیم دو پرتو نور موردنظر خود را موازی با هم در نظر بگیریم. بنابراین اینکه دو موج رسیده به نقطه $$P$$ هم‌فاز هستند یا نه، به اختلاف راه طی شده بستگی دارد و لازم است مانند پراش از تک شکاف، دو حالت تداخل سازنده و ویرانگر را برای ادامه محاسبات در نظر بگیریم.

فرمول پراش از دو شکافی یانگ در تداخل سازنده

اگر بخواهیم بدانیم برای تداخل سازنده امواج پراشیده شده از دو شکافی یانگ، فرمول پراش چیست، کافی است اختلاف راه به‌دست آمده در بخش قبل را با صفر یا مضرب صحیحی از طول موج برابر در نظر بگیریم:

$$\delta= dsin\theta=m\lambda$$

• $$m$$: عدد صحیح به صورت $$0, \pm1, \pm2, ...$$
• $$\lambda$$: طول موج جبهه موج فرودی
• $$d$$: فاصله دو شکافی یانگ از هم
• $$\theta$$: زاویه پراش

به $$m$$ مرتبه پراش هم گفته می‌شود. مرتبه صفر ($$m=0$$) معادل است با بیشترین شدت نور پراشیده شده که منطبق است با مرکز پرده در نقطه $$O$$ و زاویه پراش $$\theta=0$$. اولین مرتبه پراش یا $$m=\pm1$$ در تداخل سازنده، معادل است با اولین حلقه‌ روشنی که پس از حلقه روشن مرکزی در بالا و پایین آن روی پرده مشاهده می‌شود.

فرمول پراش از دو شکافی یانگ در تداخل ویرانگر

تداخل ویرانگر امواج نوری پراشیده شده از دو شکافی یانگ، زمانی رخ می‌دهد که اختلاف راه هر دو پرتو رسیده به یک نقطه مشخص روی پرده برابر با مضرب صحیح و فردی از طول موج شود:

$$\delta= dsin\theta=(m+\frac{1}{2})\lambda$$

• $$m$$: عدد صحیح به صورت $$0, \pm1, \pm2, ...$$
• $$\lambda$$: طول موج جبهه موج فرودی
• $$d$$: فاصله دو شکافی یانگ از هم
• $$\theta$$: زاویه پراش

رابطه بالا به این معنا است که دو موج فرضی ما وقتی به نقطه $$P$$ می‌رسند، $$180$$ درجه اختلاف فاز دارند. نتیجه تداخل ویرانگر، مشاهده حلقه‌های تاریک روی پرده است. شکل زیر به‌خوبی نشان می‌دهد که چگونه اختلاف راهی برابر با $$\delta=\frac{\lambda}{2}$$ برای $$m=0$$ منجر به شکل‌گیری تداخل ویرانگر می‌شود، در حالی که اختلاف راه $$\delta=\lambda$$ در $$m=1$$ به ما تداخل سازنده خواهد داد:

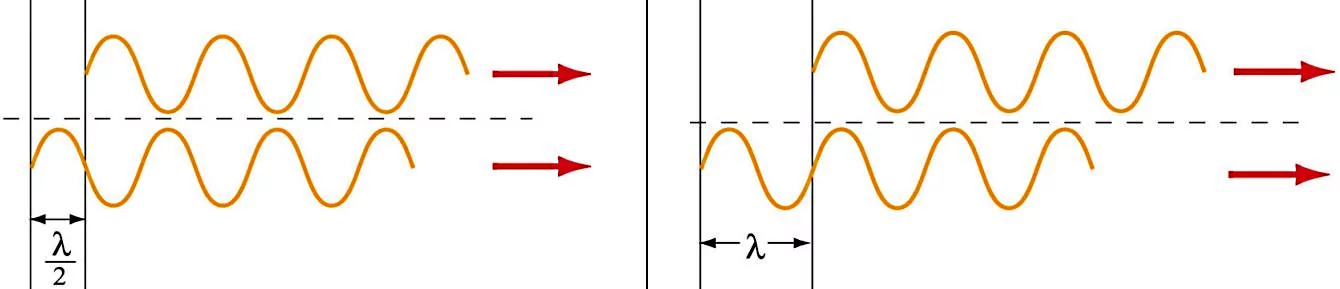
نکته: اگر فرمول‌های پراش از دو شکافی و تک شکاف را با هم مقایسه کنید، متوجه خواهید شد که رابطه تداخل سازنده و ویرانگر در این دو نوع پراش کاملا برعکس هم است.

انواع پراش چیست؟

تا اینجا یاد گرفتیم تعریف پراش چیست و دیدیم که برای محاسبه مکان قرار گرفتن کمترین یا بیشترین شدت‌‌ امواج پراشیده شده از چه فرمول‌هایی می‌توانیم استفاده کنیم. در این بخش قصد داریم انواع پراش را معرفی کنیم و در ادامه به توضیح تفاوت آن‌ها با هم بپردازیم. پراش دو نوع دارد:

• پراش فرانهوفر
• پراش فرنل

پراش فرانهوفر چیست؟

پراش فرانهوفر زمانی اتفاق می‌افتد که فاصله بین شکاف‌ها و پرده نمایش الگوی تداخلی یا الگوی پراش، خیلی خیلی زیاد باشد. نتیجه این فاصله بالا، موازی بودن امواج پراشیده شده است. به همین علت معمولا برای مشاهده امواج نوری پراشیده شده روی پرده و آشکارسازی پراش فرانهوفر آن‌ها، از عدسی‌ محدب استفاده می‌شود. قرار گرفتن عدسی محدب بین شکاف و پرده کمک می‌کند تا پرتوهای نور روی پرده همگرا شوند.

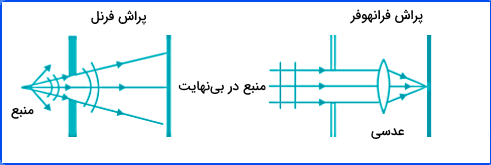
پراش فرنل چیست؟

در مقایسه با پراش فرانهوفر، در پراش فرنل فاصله بین شکاف و پرده خیلی زیاد نیست. در این حالت شکل امواج پراشیده شده کروی در نظر گرفته می‌شود. دقت کنید در پراش فرانهوفر هم بلافاصله پس از پراش و در فاصله کمی از شکاف، شکل امواج کروی است. اما در فواصل خیلی دور از شکاف، امواج به‌صورت خطوط مستقیم و موازی با هم در خواهند آمد.

مسیر یادگیری اپتیک امواج با فرادرس

چنانچه علاقه‌مند هستید با جنبه‌های مختلف اپتیک موجی در سطح دانشگاهی آشنا شده و کاربردهای پدیده‌های مختلف امواج مانند پراش را بهتر یاد بگیرید، در این بخش چند فیلم آموزشی از مجموعه فرادرس را به شما معرفی می‌کنیم تا با مشاهده آن‌ها اطلاعات و مهارت خوبی در این زمینه کسب کنید:

1. فیلم آموزش رایگان پراش در فیزیک پایه ۳ فرادرس
2. فیلم آموزش فیزیک پایه ۳ فرادرس
3. فیلم آموزش فیزیک پایه ۳ – حل تمرین فرادرس
4. فیلم آموزش فیزیک مدرن با رویکرد حل مساله فرادرس
5. فلیم آموزش رایگان انتشار امواج الکترومغناطیسی فرادرس
6. فیلم آموزش رایگان امواج و ارتعاشات فرادرس
7. فیلم آموزش اپتیک یا نورشناسی فرادرس
8. فیلم آموزش پراکندگی امواج فرادرس
9. فیلم آموزش میدان ها و امواج فرادرس

آزمون پراش

در این مطلب از مجله فرادرس آموختیم پراش چیست و روش‌های ایجاد آن به چه صورت است. اگر می‌خواهید میزان یادگیری و تسلط خود به مباحث این مطلب را بیازمایید، می‌توانید به ده سوال چهار گزینه‌ای زیر که در قالب یک آزمون برای شما تهیه شده است، پاسخ دهید. در انتها با کلیک روی گزینه «دریافت نتیجه آزمون»، نمره نهایی شما قابل مشاهده است.