نوسانات میرا — به زبان ساده

هر انسانی در زندگی یک بار تجربه‌ سوار شدن تاب را دارد و احتمالاْ این سوال را از خود پرسیده که چرا اگر نیروی خارجی به تاب وارد نشود، حرکت تاب بعد از مدتی کٌند و سپس متوقف می‌شود؟ پاسخ به این پرسش با شناخت نوسانات میرا امکان‌پذیر است. در این آموزش نوسانات میرا را مطالعه کرده و معادلات حرکت آن را مورد بررسی قرار می‌دهیم.

نوسانات میرا

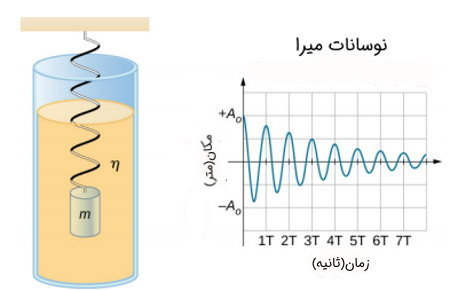
فرض کنید جسمی به جرم $$\large m$$ به فنری با ضریب سختی $$\large k$$ متصل است (شکل ۲)، جسم به صورت متناوب حول نقطه $$A_{0}$$ به عنوان دامنه ابتدایی حرکت بالا و پایین می‌رود و اطراف نقطه‌ تعادل حرکت نوسانی انجام می‌دهد.

فیلم آموزش فیزیک پایه 3 – جامع و کاربردی در فرادرس

کلیک کنید

به دلیل ویسکوزیته‌ مایعی که جسم در آن قرار گرفته است، دامنه‌ نوسانات میرا به مرور زمان کوچک می‌شود. با این حال، اگر نیرویی که باعث میرایی حرکت است، کوچک باشد دوره تناوب و فرکانس حرکت تقریبا ثابت باقی خواهد ماند و جسم در یک بازه‌ زمانی، حرکتی نزدیک به حرکت نوسانی ساده را تجربه خواهد کرد. با این حال، به دلیل عدم پایستگی نیروی میرایی، انرژی در سیستم فنر به گرما تبدیل شده و باعث کاهش دامنه‌ حرکت می‌شود.

معادلات حرکت نوسانی میرا

نیروی خالص وارد بر جسم در شکل ۲، نیروی کشسانی فنر و نیروی میرایی است. اگر این سوال ذهنتان را درگیر کرده که «چرا از نیروی وزن صحبتی نشده است؟» باید بیان کرد که نیروی وزن تنها برای شروع حرکت از حالت سکون بر جسم اثر می‌گذارد و در معادلات حرکت نوسانی تاثیری ندارد. با استفاده از قانون دوم نیوتن داریم:

$$\large ma = -bv - kx\quad\quad (1)$$

فیلم آموزش مکانیک تحلیلی 1 Analytical Mechanics در فرادرس

کلیک کنید

نیروی میرایی ($$\large -bv$$) وابسته به سرعت جسم است و خلاف جهت نیروی کشسانی فنر به سیستم نیرو وارد می‌کند. $$\large -b$$ را ثابت میرایی می‌نامیم. با استفاده از رابطه‌ میان مکان، سرعت و شتاب رابطه‌ (۱) به شکل زیر در می‌آید:

$$\large m \frac{d^{2} x}{dt^{2}} + b \frac{dx}{dt} + kx = 0\quad\quad (2)$$

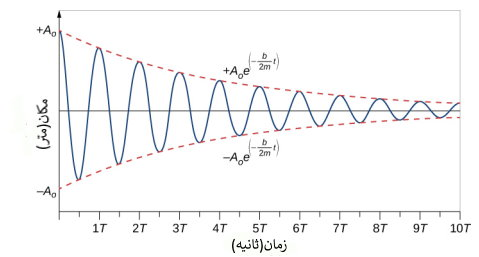
برای حل این معادله، نمودار تغییرات مکان بر حسب زمان را با استفاده از نرم‌افزار‌های رسم منحنی (برای مثال متلب) می‌توان رسم کرد. منحنی شکل (۳) نمایشگر حرکت یک تابع کسینوسی با دامنه‌ نمایی به صورت $$\large A_0e^{−\alpha t}$$ است که در آن $$\large \alpha = \frac{b}{2m}$$ است. بدین ترتیب جواب معادله‌ (۲) برابر است با:

$$\large x(t) = A_{0} e^{- \frac{b}{2m} t} \cos (\omega t + \phi_{0}) \quad\quad (3)$$

می‌توان نشان داد که معادله‌ (۳)، پیش‌بینی درستی از جواب معادله‌ (۲) است. برای اثبات این موضوع از رابطه‌ (۳) بر حسب زمان مشتق می‌گیریم و در معادله‌ (۲) قرار می‌دهیم. با انجام محاسبات، مشخص می‌شود که معادله‌ (۳) در صورتی جواب معادله (۲) است که $$\large \omega = \sqrt{\frac{k}{m} - \left(\dfrac{b}{2m}\right)^{2}}$$ باشد.

تفسیر جواب‌های معادلات حرکت

در حرکت نوسانی ساده که نیروی میرایی وجود ندارد، سرعت زاویه‌ای یا فرکانس زاویه‌ای حرکت برابر است با:

$$\large \omega_{0} = \sqrt{\frac{k}{m}}$$

در حالی که فرکانس زاویه‌ای برای حرکت نوسانی میرا به صورت زیر است:

$$\large \omega = \sqrt{\omega_{0}^{2} - \left(\dfrac{b}{2m}\right)^{2}}  \quad (4)$$

معادله‌ (۴) نشان می‌دهد که با افزایش $$\large b$$، فرکانس کوچک و کوچکتر  و در $$\large b=\sqrt{4mk}$$ صفر می‌شود. در نهایت با ادامه‌ روند افزایش $$\large b$$ فرکانس موهومی ‌خواهد شد.

فرکانس حرکت نوسانی میرا

شکل (۴)، تغییرات مکان بر حسب زمان به ازای مقادیر مختلف $$\large b$$ را نشان می‌دهد.

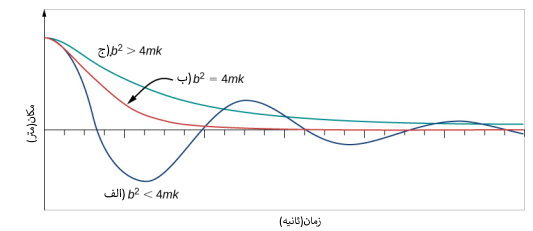
برای حرکت نوسانی میرا می‌توان سه حالت را معرفی کرد:

1. اگر ضریب میرایی یا $$\large b$$ کوچک باشد ($$\large b<\sqrt{4mk}$$): در این حالت جسم حرکت نوسانی انجام می‌دهد و دامنه‌ حرکت به صورت نمایی کاهش می‌یابد. این حالت را «زیرمیرایی» (Underdamped) می‌گوییم که در شکل (۴) با (الف) نمایش داده شده است. در این حالت با کاهش دامنه‌ حرکت، جسم در نهایت به سکون می‌رسد.
2. اگر ثابت میرایی برابر با مقدار بحرانی باشد ($$\large b=\sqrt{4mk}$$): سیستم در حالت «میرایی بحرانی» (Critically Damped) است که در شکل (۴) با (ب) نمایش داده شده است. یکی از کاربردهای سودمند میرایی بحرانی در کمک فنرهای یک خودرو است. در این حالت خودرو نوسان نمی‌کند و خیلی سریع به حالت تعادل می‌رسد.
3. اگر ثابت میرایی برابر با مقدار بحرانی باشد ($$\large b>\sqrt{4mk}$$): این حالت که در شکل (۴) با (ج) نشان داده شده است را «فوق میرایی» (Overdamped) می‌نامیم. در این حالت سیستم بعد از مدت زمان طولانی به تعادل می‌رسد.

برای درک بیشتر مطالب گفته شده در این بخش، این آموزش را با حل یک مثال از نوسانات میرا به پایان می‌رسانیم.

مثالی از نوسانات میرا

سیستمی همانند شکل (۲) در نظر بگیرید که در آن ثابت فنر برابر با $$k=32 (\frac{N}{m})$$، جرم جسم $$m=0.5(kg)$$ و ثابت میرایی $$b=1(\frac{Ns}{m})$$ است. معادله‌ حرکت را برای شرایط مرزی $$x(0)=2(m)$$ و $$v(0)=0$$ به دست آورید.

حل: با توجه به مقادیر داده شده، در ابتدا باید نوع میرایی حرکت را بررسی کنیم و داریم:

$$\large b^{2}-4mk< 0$$

در نتیجه، نوسانگر در حالت زیرمیرایی قرار دارد و دارای جوابی به شکل معادله‌ (۳) است. بدین ترتیب، فرکانس حرکت برابر است با:

$$\large \omega = \sqrt{\omega_{0}^{2} - \left(\dfrac{b}{2m}\right)^{2}}=\sqrt{63}=7.94$$

با قرار دادن در شرایط اولیه تابع داریم:

$$\large x(0) = A\cos(−\phi_{0}) = 2\rightarrow A =2\cos \phi_{0}$$

$$\large v(0) =−A(\frac{1}{2}\gamma\cos \phi_{0} + \dot{ω}\sin(- \phi_{0}))= 0 \rightarrow \phi_{0} = 0.125$$

که $$\gamma=\frac{b}{2m}$$ و معادله‌ حرکت به شکل زیر به دست می‌آید:

$$\large x(t) =2.02 e^{-t}\cos(7.94 t-0.125)$$