قرینه عدد چیست؟ – ریاضی به زبان ساده + مثال و تمرین
قرینه عدد، نمایش آن عدد با علامت منفی است. اگر یک عدد را در (۱-) ضرب کنیم، قرینه آن به دست میآید. تمام اعداد به غیر از عدد صفر، قرینه دارند. یکی از روشهای ساده برای یادگیری مفهوم قرینه اعداد، استفاده از محور اعداد است. در این مقاله، سوال «قرینه عدد چیست؟» را به طور کامل پاسخ میدهیم. سپس، به حل چندین تمرین و مثال متنوع میپردازیم. علاوه بر این، رابطه و کاربرد قرینه اعداد در رسم قرینه شکلها را نیز مورد بررسی قرار میدهیم.
قرینه در ریاضی چیست ؟
در ریاضیات و هندسه، قرینه یک شکل، بازتاب آن نسبت به یک خط یا نقطه است. قرینه را میتوان در شکلهای دارای تقارن (تقارن محوری، تقارن مرکزی، تقارن انتقالی) مشاهده کرد.

تقارن محوری یا بازتابی (شکل راست در تصویر بالا)، مثال بسیار خوبی برای درک مفهوم قرینه در ریاضیات است. مفهوم قرینه، به اشکال هندسی محدود نمیشود. اعداد نیز میتوانند دارای قرینه باشند.
قرینه عدد چیست؟
برای درک مفهوم قرینه عدد، محوری را مشابه با تصویر زیر رسم میکنیم.

با استفاده از خطکش، مرکز این محور را علامت میزنیم و عدد ۰ را در پایین آن مینویسیم.

از سمت راست، به ازای هر سانتیمتر، یک علامت بر روی محور میگذاریم. سپس، این علامتها را به ترتیب با رنگ آبی شمارهگذاری میکنیم.

همین کار را برای سمت چپ عدد صفر انجام میدهیم. اعداد این سمت را با رنگ قرمز شمارهگذاری میکنیم.

در مطلب «قرینه شکل چیست»، گفتیم که اگر شکلهای قرینه را از روی محور تقارنشان تا بزنیم، هر دو طرف شکل به طور کامل بر روی یکدیگر منطبق میشوند. در تصویر بالا، اگر محور اعداد را از روی عدد صفر تا بزنیم، اعداد سمت راست بر روی اعداد سمت چپ منطبق میشوند.
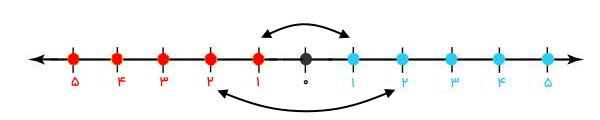
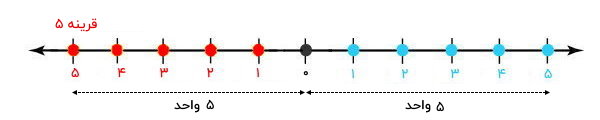
با تا زدن محور از روی ۰، عدد ۱ در سمت راست محور بر روی عدد ۱ در سمت چپ محور قرار میگیرد. عدد ۲ در سمت راست بر روی عدد ۲ در سمت چپ و عدد ۳ در سمت راست بر روی عدد ۳ در سمت چپ منطبق میشود. برای اعداد دیگر نیز دقیقا همین اتفاق رخ میدهد. به این ترتیب، میگوییم عدد ۱ در سمت چپ محور، قرینه عدد ۱ در سمت راست محور است یا عدد ۱ در سمت راست محور، قرینه عدد ۱ در سمت چپ محور است. تصویر زیر، قرینه اعداد را نمایش دادهایم.
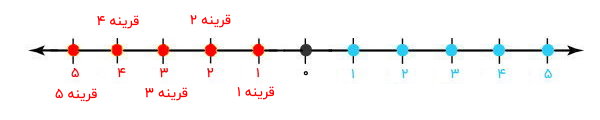
برای اینکه قرینه عدد بر روی محور اعداد را به دست بیاوریم، باید به اندازه همان عدد در سمت چپ صفر حرکت کنیم. به عنوان مثال، قرینه عدد ۵، به اندازه ۵ واحد در سمت چپ صفر قرار دارد.
تمرین ۱: تعیین قرینه عدد بر روی محور
قرینه عدد ۶ را بر روی محور زیر نمایش دهید.

برای تعیین محل قرارگیری قرینه عدد ۶ در محور بالا، ابتدا فاصله عدد ۰ تا ۶ را با استفاده از خطکش به دست میآوریم.

خطکش، عدد ۱۴ را نمایش میدهد. بنابراین، فاصله ۱۴ سانتیمتری از سمت چپ عدد ۰ را علامت میزنیم.

محل علامتگذاری شده در سمت چپ محور اعداد، قرینه عدد ۶ است.

در ریاضیات، قرینه اعداد را با یک علامت مخصوص نمایش میدهد. در بخش بعدی، به معرفی این علامت و کاربرد آن در نمایش قرینه اعداد میپردازیم.
عدد مثبت و عدد منفی چیست ؟
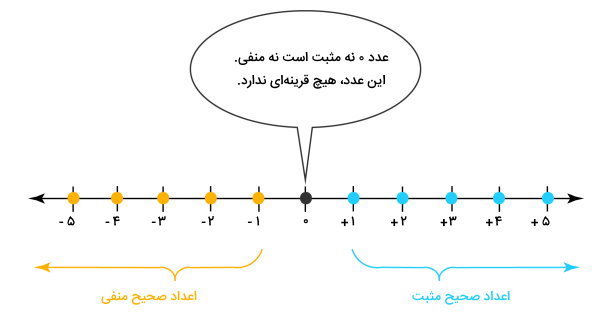
در ریاضیات، به اعداد سمت راست محور اعداد، عدد مثبت و به اعداد سمت چپ، عدد منفی میگویند. اعداد مثبت را با علامت بهعلاوه (+) و اعداد منفی را با علامت منها (-) نمایش میدهند. به این ترتیب، محور اعداد به صورت زیر رسم و عددگذاری میشود.
رابطه بین اعداد مثبت و منفی با قرینه عدد
محور اعداد زیر را در نظر بگیرید. اعداد مثبت این محور در سمت راست و اعداد منفی آن در سمت چپ قرار دارند.

بر اساس مطالب بخش قبل، برای تعیین قرینه هر عدد، باید به اندازه فاصله آن تا عدد ۰، به سمت چپ حرکت کنیم. به عنوان مثال، به منظور مشخص کردن محل قرینه عدد ۱+، به اندازه یک واحد از روی عدد ۰ به سمت چپ میرویم.

با توجه به تصویر بالا، عدد ۱- (میخوانیم منفیِ یک) قرینه عدد ۱+ (میخوانیم مثبتِ یک) است. برای اعداد دیگر نیز میتوانیم بگوییم:
- قرینه عدد ۲+ برابر با ۲- است.
- قرینه عدد ۳+ برابر با ۳- است.
- قرینه عدد ۴+ برابر با ۴- است.
- قرینه عدد ۵+ برابر با ۵- است.
در نتیجه، قرینه هر عدد، با منفی آن عدد برابر است. توجه داشته باشید که میتوانستیم جملههای بالا را به صورت زیر نیز بنویسیم:
- قرینه عدد ۲- برابر با ۲+ است.
- قرینه عدد ۳- برابر با ۳+ است.
- قرینه عدد ۴- برابر با ۴+ است.
- قرینه عدد ۵- برابر با ۵+ است.
از جملههای بالا و جملههای قبلی میتوانیم نتیجه بگیریم که قرینه قرینه یک عدد، برابر با خود همان عدد میشود. به عبارت دیگر، منفی و مثبت یک عدد، قرینه یکدیگرند.
تمرین ۲: قرینه قرینه عدد
قرینه قرینه عدد ۶۲۴ چند است؟
قرینه عدد ۶۲۴ برابر میشود با:
۶۲۴- = ۶۲۴ × (۱-)
بنابراین، قرینه قرینه عدد ۶۲۴ نیز برابر است با:
۶۲۴ = (۶۲۴-) × (۱-)
در نتیجه، قرینه عدد ۶۲۴ برابر با خودش خواهد بود.
قرینه عدد در مجموعه اعداد چیست ؟
مجموعه اعداد، به اعدادی گفته میشود که دارای ویژگیهای مشترک هستند. در این بخش، قرینه اعداد در مجموعه اعداد صحیح و اعداد حقیقی را مورد بررسی قرار میدهیم.
قرینه اعداد صحیح چیست ؟
اعداد صحیح، مجموعه اعداد مثبت، منفی و صفر هستند. در این مجموعه، هیچ عدد کسری یا اعشاری وجود ندارد. مجموعه اعداد صحیح مثبت، همان اعداد طبیعی و زیرمجموعه اعداد حسابی (صفر و اعداد صحیح مثبت) است. به همین دلیل، برای نوشتن اعضای آن، نیازی به استفاده از علامت بهعلاوه نیست. به این ترتیب، اعداد صحیح معمولا به صورت زیر نمایش داده میشوند:
از اینرو، هنگام نوشتن اعداد صحیح مثبت میتوانیم علامت بهعلاوه کنار آنها را حذف کنیم. به عنوان مثال، ۳+ به صورت ۳ نیز نوشته میشود. در زمان تعیین قرینه اعداد نیز میتوانیم بگوییم عدد ۳-، قرینه عدد ۳ است. به منظور محاسبه قرینه هر یک از اعداد صحیح، عدد مورد نظر را در (۱-) ضرب میکنیم. به عنوان مثال، قرینه عدد ۵ با استفاده از رابطه زیر تعیین میشود:
(۵+) × (۱-) = قرینه ۵
حاصلضرب عدد مثبت در منفی یا منفی در مثبت، منفی میشود. از اینرو، داریم:
۵- = قرینه ۵
اکنون فرض کنید میخواهیم قرینه عدد ۹- را به دست بیاوریم. به این منظور، عدد ۹- را در ۱- ضرب میکنیم:
(۹-) × (۱-) = قرینه ۹-
حاصلضرب عدد منفی در منفی، مثبت میشود. بنابراین داریم:
۹+ = قرینه ۹-
تمرین ۳: محاسبه قرینه عدد صحیح
قرینه عدد ۱۵۷۸ و ۴۳- را به دست بیاورید. سپس، قرینه این دو عدد را با هم مقایسه کنید. چه نتیجهای از این مقایسه میگیرید؟
قرینه هر عدد صحیح، از ضرب آن عدد در عدد (۱-) به دست میآید. به این ترتیب، داریم:
۱۵۷۸ - = ۱۵۷۸ × (۱-) = قرینه ۱۵۷۸
۴۳ = (۴۳-) × (۱-) = قرینه ۴۳
در محور اعداد، هر چه یک عدد منفی به ۰ نزدیکتر باشد، اندازه آن عدد بزرگتر است. از میان اعداد بالا، ۴۳- به ۰ نزدیکتر است. از اینرو:
برای نتیجهگیری نهایی، اعداد مورد سوال را نیز با یکدیگر مقایسه میکنیم:
از این دو رابطه میتوانیم نتیجه بگیریم که اگر یک عدد از عدد دیگر بزرگتر باشد، قرینه آن عدد از قرینه عدد دیگر کوچکتر خواهد بود. اعداد بخشهای قبلی، همه زیرمجموعهای از اعداد صحیح بودند. در ریاضیات، مجموعه بزرگتری از اعداد وجود دارد که در ادامه به معرفی آن و قرینه اعداد موجود در آن میپردازیم.
قرینه اعداد حقیقی چیست ؟
اعداد حقیقی، بزرگترین مجموعه اعداد است و تمام مجموعههای دیگر از قبیل اعداد صحیح، حسابی، طبیعی، گویا و گنگ را دربرمیگیرد. اعداد گویا، اعدادی هستند که میتوان آنها را به صورت نسبت دو عدد صحیح نمایش داد.
اعداد زیر، در مجموعه اعداد گویا قرار میگیرند:
۱, ۱۲/۳۸, -۰/۸۶۲۵, , -۱۹۸
قرینه عدد گویا نیز مانند قرینه عدد صحیح، از ضرب هر عدد در (۱-) به دست میآید. به عنوان مثال، اعداد بالا را در نظر بگیرید. قرینه هر یک از این اعداد برابر است با:
۱- = قرینه ۱
۱۲/۳۸- = قرینه ۱۲/۳۸
۰/۸۶۲۵ = قرینه ۰/۸۶۲۵-
= قرینه
۱۹۸ = قرینه ۱۹۸-
اعمال ریاضی بر روی قرینه عدد
قرینه اعداد، ویژگیهای متعددی دارند. با اجرای اعمال ریاضی بر روی یک عدد و قرینه آن، نتایج جالبی به دست میآیند که در ادامه به آن میپردازیم.
جمع عدد و قرینه عدد چیست ؟
جمع یک عدد با قرینه خودش، همواره برابر با ۰ میشود. به عنوان مثال، عدد ۵۵/۵ را در نظر بگیرید. قرینه این عدد برابر با ۵۵/۵- است. بنابراین داریم:
۰ = ۵۵/۵ - ۵۵/۵ =(۵۵/۵-) + ۵۵/۵

تفریق عدد و قرینه عدد چیست ؟
تفریق یا اختلاف یک عدد با قرینهاش، برابر با حاصلضرب آن عدد در عدد ۲ است. در بخشهای قبلی دیدیم که برای به دست آوردن قرینه یک عدد، باید به اندازه فاصله آن تا مرکز محور اعداد (عدد ۰) در سمت دیگر عدد ۰ جلو برویم. به این ترتیب، فاصله عدد تا قرینه عدد، دو برابر فاصله عدد تا مرکز محور اعداد میشود. به عنوان مثال، عدد ۷۱- را در نظر بگیرید. قرینه این عدد برابر با عدد ۷۱ است. اختلاف این دو از رابطه زیر به دست میآید:
۱۴۲ - = ۷۱ - (۷۱-)
حاصل تفریق بالا با حاصلضرب پایین برابر است:
۱۴۲ - = (۷۱-) × ۲
اگر فاصله عدد تا قرینهاش را بخواهیم، باید حاصل تفریق یا ضرب بالا را به صورت مثبت (قدر مطلق) بیان کنیم. بر این اساس، فاصله ۷۱- تا قرینهاش، برابر با ۱۴۲ خواهد بود.
تقسیم عدد و قرینه عدد چیست ؟
اگر عددی را بر قرینهاش تقسیم کنیم، عدد به دست آمده، همواره برابر با (۱-) خواهد بود. به عنوان مثال، عدد را در نظر بگیرید. قرینه این عدد برابر با است. اگر این دو عدد را بر هم تقسیم کنیم، خواهیم داشت:
ضرب عدد و قرینه عدد چیست ؟
ضرب یک عدد در قرینهاش، قرینه توان دو آن عدد میشود. به عنوان مثال، عدد ۸ را در نظر بگیرید. قرینه این عدد برابر با ۸- است. با ضرب ۸ در قرینهاش داریم:
۶۴- = (۸-) × ۸
این نتیجه را به خاطر داشته باشید. عدد ۸ را به توان دو میرسانیم:
۶۴ = ۸۲
قرینه عدد ۶۴ برابر با ۶۴- است. بنابراین، حاصلضرب عدد در قرینه، برابر با قرینه عدد به توان دو شد.
قدر مطلق قرینه عدد چیست ؟
به فاصله یک عدد با مبدأ محور اعداد، قدر مطلق آن عدد میگویند. به عنوان مثال، فاصله عدد ۳ تا عدد ۰ ( مبدأ محور اعداد) برابر با ۳ واحد است. بنابراین، قدر مطلق عدد ۳ برابر با ۳ میشود. از طرف دیگر، فاصله عدد ۳- تا عدد ۰ نیز برابر با ۳ واحد است. از اینرو، قدر مطلق عدد ۳- نیز برابر با ۳ میشود.
به این ترتیب، قدر مطلق قرینه عدد برابر با خود آن عدد برابر است. در محاسبه فاصله بین عدد و قرینه آن، از مفهوم قدر مطلق استفاده میشود.
تمرین ۴:انجام عمل های ریاضی بر روی قرینه عدد
عدد کسری سهچهارم را در نظر بگیرید. جمع، تفریق، تقسیم و ضرب و فاصله این عدد با قرینهاش را حساب کنید.
قرینه عدد سهچهارم برابر است با:
جمع سهچهارم با قرینهاش برابر با صفر است:
حاصل تفریق سهچهارم با قرینهاش، از ضرب این عدد در ۲ به دست میآید:
تقسیم سهچهارم بر قرینهاش، برابر با (۱-) میشود:
ضرب سهچهارم در قرینهاش نیز برابر با منفی توان دوی این عدد است:
فاصله سهچهارم تا قرینهاش، برابر با دو برابر فاصله سهچهارم تا عدد ۰ میشود:
تمرین ۵:محاسبه فاصله یک عدد تا قرینه عدد دیگر
فاصله عدد ۱۱ تا قرینه عدد ۱۳ را تعیین کنید.
قرینه عدد ۱۳ برابر با ۱۳- است. میخواهیم فاصله عدد ۱۱ تا ۱۳- را به دست بیاوریم. به این منظور، عدد بزرگتر (۱۱) را از عدد کوچکتر (۱۳-) کم میکنیم. به این ترتیب داریم:
۲۴ = ۱۳ + ۱۱ = (۱۳-) - ۱۱
در نتیجه، فاصله عدد ۱۱ تا قرینه عدد ۱۳ برابر با ۲۴ واحد است.
قرینه یک عدد نسبت به عدد دیگر چیست ؟
در بخشهای قبلی، تعریف عمومی قرینه عدد را مورد بررسی قرار دادیم و چند مثال حل کردیم. بر اساس تعریف عمومی، قرینه یک عدد، با توجه به مبدأ محور اعداد، یعنی عدد ۰، تعیین میشود. به عبارت دیگر، عدد ۰، مرکز تقارن است. در برخی از مسائل، ممکن عدد دیگری را به عنوان مبنای قرینه تعریف کنند. به این ترتیب، باید قرینه عدد را نسبت به عددی به غیر از ۰ به دست آورد. به عنوان مثال، فرض کنید در محور اعداد زیر، عدد 2، مبنای تعیین قرینه اعداد است.
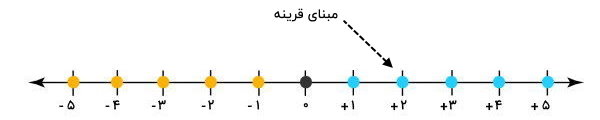
اکنون میخواهیم قرینه یکی از اعداد مانند عدد 5 را نسبت به عدد 2 به دست بیاوریم. به این منظور، ابتندا باید فاصله عدد مورد نظر تا عدد 2 را تعیین کنیم. فاصله عدد 5 تا عدد 2 برابر با 3 واحد است.
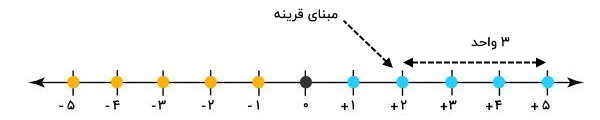
اکنون، به همان اندازه (در اینجا 3 واحد)، در طرف دیگر عدد دو به سمت چپ میرویم.
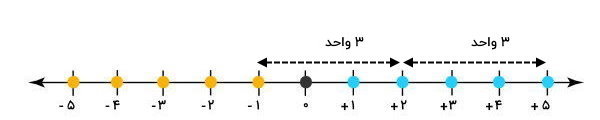
به این ترتیب، به عدد (1-) میرسیم. در نتیجه، قرینه عدد 5 نسبت به عدد 2 برابر با (1-) است. برای اعداد دیگر نیز میتوانیم به همین روش، قرینه عدد نسبت به عدد دیگر را به دست بیاوریم.
تفاوت قرینه و معکوس یک عدد چیست ؟
اگر جای صورت و مخرج یک عدد کسری را با هم عوض کنیم، معکوس عدد به دست میآید. در صورتی که قرینه عدد، با ضرب آن در (۱-) حاصل میشود. برخی از دانشآموزان، مفهوم قرینه عدد را با معکوس عدد اشتباه میگیرند. عدد کسری زیر را در نظر بگیرید:
قرینه این عدد برابر است با:
معکوس این عدد برابر با کسر زیر میشود:
قرینه معکوس عدد عبارت است از:
حاصلضرب قرینه عدد در معکوس آن برابر با (۱-) میشود.
استفاده از قرینه عدد در رسم قرینه شکل
قرینه شکل، بازتاب یک شکل نسبت خط یا نقطه است. به عنوان مثال، تصویر زیر، قرینه یک مثلث را نسبت به یک محور عمودی نمایش میدهد.
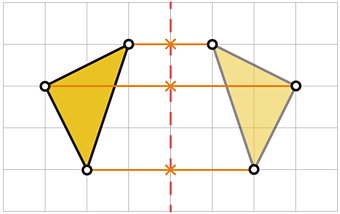
روشهای مختلفی برای رسم قرینه شکلها وجود دارد. استفاده از صفحه شطرنجی و مختصات نقاط شکل بر روی دستگاه محورهای مختصات، یکی از سادهترین روشها برای انجام این کار است. کاربرد قرینه اعداد در رسم قرینه شکل را با یک مثال توضیح میدهیم. دستگاه محورهای مختصات زیر را در نظر بگیرید.

فرض کنید میخواهیم قرینه نقطه (الف) را نسبت به محور عمودی، محور افقی و مرکز مختصات به دست بیاوریم.
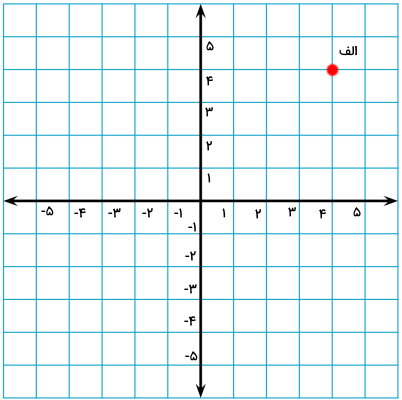
مختصات نقطه (الف) به صورت نوشته میشود:
عدد بالا، طول نقطه و عدد پایین، عرض نقطه را نمایش میدهد. برای اینکه قرینه این نقطه را نسبت به محور عمودی به دست بیاوریم، طول نقطه را قرینه میکنیم:
تصویر زیر، مختصات نقطه بالا در دستگاه محورهای مختصات است. این نقطه، قرینه (الف) را نشان میدهد.
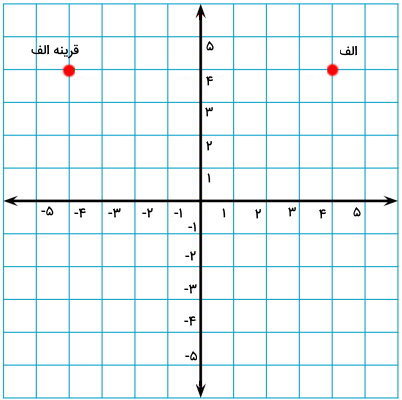
به منظور تعیین قرینه نقطه (الف) نسبت به محور افقی، باید عرض مختصات آن را قرینه کنیم:
مختصات نقطه بالا در دستگاه محورهای مختصات، به صورت زیر نمایش داده میشود. این نقطه، همان قرینه (الف) است.
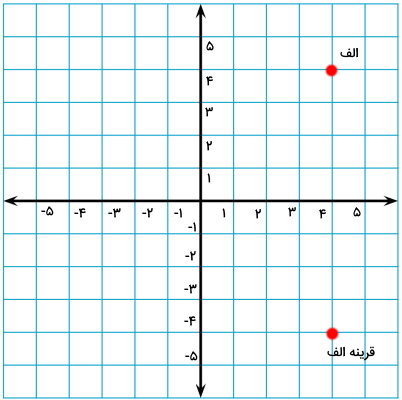
در نهایت، اگر بخواهیم قرینه نقطه (الف) را نسبت به مبدا مختصات به دست بیاوریم، هر دو عدد مختصات (طول و عرض) را قرینه میکنیم:
محل قرارگیری نقطه بالا به شکل زیر است. این نقطه، قرینه (الف) را نمایش میدهد.
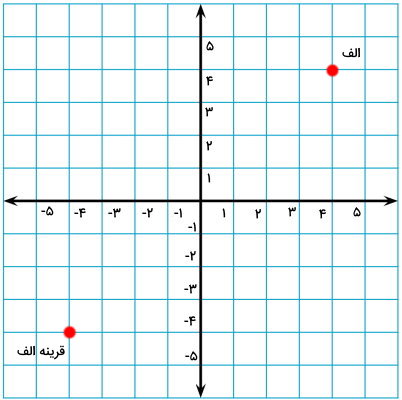
این مثال، کاربرد قرینه عدد در رسم قرینه شکلها بود. اگر محل قرارگیری خط تقارن یا نقطه تقارن مانند مثال نبود، میتوانید مختصات را به طور موقت به محل مناسب انتقال دهید یا یک مبدأ جدید برای مختصات تعیین کنید.
سوالات متداول در رابطه با قرینه عدد
در این بخش، به برخی از سوالات پرتکرار در رابطه قرینه عدد به طور خلاصه پاسخ میدهیم.
قرینه قرینه عدد صحیح چه می شود ؟
قرینه قرینه عدد صحیح، خود آن عدد میشود.
جمع هر عدد با قرینه آن عدد چه می شود ؟
جمع هر عدد با قرینه آن عدد برابر با صفر میشود.
قرینه عدد چهار چند است ؟
قرینه عدد چهار، منفیِ چهار است.
قرینه کدام عدد با خودش برابر است ؟
قرینه عدد صفر برابر با خودش است.
کدام عدد قرینه ندارد ؟
عدد صفر، تنها عددی است که قرینه ندارد.
حاصل تقسیم یک عدد بر قرینه آن چیست ؟
حاصل تقسیم یک عدد بر قرینه آن، برابر با ۱- است.
قدر مطلق قرینه عدد چند است ؟
قدر مطلق قرینه عدد، خود آن عدد است.
حاصلضرب هر عدد در قرینه ی معکوس آن برابر با چیست ؟
حاصلضرب هر عدد در قرینه ی معکوس آن برابر با (۱-) است.
آزمون قرینه اعداد
۱. برای پیدا کردن قرینه یک عدد صحیح، کدام عمل سادهتر و رایجتر برای این کار معرفی شده است؟
اضافه کردن عدد به خودش
تقسیم عدد بر دو
جمع عدد با صفر
ضرب عدد در (۱-)
برای یافتن قرینه عدد صحیح کافی است همان عدد را در «(۱-)» ضرب کنیم تا علامت آن تغییر کند. این روشی است که همیشه برای محاسبه قرینه استفاده میشود. جمع عدد با صفر یا تقسیم عدد بر دو اثری روی علامت عدد و قرینه آن ندارد و اضافه کردن عدد به خودش فقط مقدار را دو برابر میکند، نه اینکه معکوس علامت را بسازد.
۲. در محور اعداد، اگر محور را از نقطه صفر تا بزنیم، چه رابطهای بین عدد و قرینهاش به دست میآید؟
فاصله عدد تا قرینهاش نصف میشود.
عدد و قرینهاش دقیقا روی هم قرار میگیرند.
عدد از محور حذف میشود و فقط قرینه باقی میماند.
عدد و قرینهاش با فاصله یک واحد از صفر جدا میشوند.
زمانی که محور اعداد از نقطه صفر تا زده شود، عدد و قرینهاش طوری روی محور قرار میگیرند که دقیقا بر هم منطبق میشوند. این به این معناست که هر عدد و قرینهاش نسبت به صفر فاصلهٔ یکسانی دارند، ولی در سمت مخالف محور اعداد هستند. پس عبارت «عدد و قرینهاش دقیقا روی هم قرار میگیرند» درست است.
۳. اگر نقطهای با مختصات (a, b) نسبت به محور x قرینه شود، مختصات جدید آن نقطه چیست؟
(-a, -b)
(a, -b)
(b, a)
(-a, b)
وقتی نقطهای با مختصات (a, b) نسبت به محور x قرینه شود، تنها علامت جزء مربوط به y یا همان b تغییر میکند و x ثابت میماند. بنابراین مختصات جدید "(a, -b)" خواهد بود. گزینههایی مانند "(-a, b)" و "(-a, -b)" مختص به قرینه نسبت به محور y یا مرکز مختصات هستند و تغییر دادن هر دو مختصه برای قرینه نسبت به محور x صحیح نیست. گزینه "(b, a)" هم یک جابجایی و نه قرینه را نشان میدهد. تنها گزینهای که قرینه صحیح نسبت به محور x را نمایش میدهد، همان "(a, -b)" است.
۴. عمل جمع یک عدد با قرینه خود چه خاصیتی را همواره ایجاد میکند و علت این ویژگی چیست؟
همیشه حاصل برابر با صفر میشود چون عدد و قرینه دقیقا وارونهاند.
همیشه جمع برابر با قرینه عدد میشود چون قرینه غالب است.
همیشه حاصل با خود عدد برابر است چون قرینه تاثیری ندارد.
حاصل جمع همیشه عددی مثبت میشود چون اعداد مخالف جمع میشوند.
وقتی یک عدد را با قرینهٔ خود جمع کنیم، «همیشه حاصل برابر با صفر میشود» چون قرینه در ریاضی به معنای وارون کردن علامت عدد است. وقتی یک عدد و وارونهاش را جمع میکنیم، جمع آنها اثر یکدیگر را خنثی کرده و نتیجه صفر خواهد بود. عبارت «خود عدد» نادرست است چون جمع با قرینه عدد را حذف میکند. بیان اینکه جمع همیشه مثبت میشود صحت ندارد، زیرا برای هر عدد مثبت یا منفی، نتیجه صفر است و نه مثبت. همچنین حاصل جمع نمیتواند همیشه برابر با «قرینه عدد» باشد، زیرا عدد و قرینه دقیقا جمعشان صفر میشود.
۵. اگر عددی مثبت داشته باشیم، قرینه آن روی محور اعداد در کدام سمت نسبت به صفر قرار میگیرد و چه علامتی خواهد داشت؟
در سمت چپ صفر با علامت منفی قرار میگیرد.
در وسط محور و بدون علامت قرار میگیرد.
در سمت راست صفر با علامت مثبت قرار میگیرد.
در هر دو سمت محور با علامت مثبت قرار میگیرد.
هنگامی که عددی مثبت باشد و بخواهیم قرینه آن را بیابیم، باید همان مقدار را به سمت دیگر صفر اما در طرف مقابل محور قرار دهیم. در این صورت قرینه عدد مثبت، به همان اندازه از صفر اما در سمت چپ قرار میگیرد و علامت آن منفی میشود. بنابراین «در سمت چپ صفر با علامت منفی قرار میگیرد» درست است. عبارت «در سمت راست صفر با علامت مثبت قرار میگیرد» مربوط به خود عدد مثبت است نه قرینه آن. عبارت «در وسط محور و بدون علامت قرار میگیرد» فقط درباره صفر صادق است. عبارت «در هر دو سمت محور با علامت مثبت قرار میگیرد» نیز اشتباه است، چون فقط اعداد مثبت در سمت راست و با علامت مثبت هستند و قرینه اعداد مثبت همواره منفی است.
۶. در اعداد کسری، تفاوت اصلی قرینه و معکوس در کدام عمل و نحوه تغییر آنها دیده میشود؟
قرینه همیشه مقدار کسر را صفر میکند اما معکوس آن را عدد صحیح میکند
قرینه صورت کسر را منفی میکند اما معکوس مقدار کسر را دو برابر میسازد
قرینه علامت کسر را تغییر میدهد ولی معکوس جای صورت و مخرج را عوض میکند
قرینه و معکوس هر دو عدد را منفی میکنند ولی ترتیب عدد فرقی ندارد
در اعداد کسری، قرینه عدد تنها علامت کسر را برعکس میکند مانند تبدیل ۲/۳ به ۳-/۲، ولی معکوس با جابجایی صورت و مخرج عمل میکند مثل تبدیل ۲/۳ به ۳/۲. قرینه صورت را منفی نمیکند و معکوس نیز مقدار کسر را دو برابر نمیسازد. همچنین، قرینه کسر را صفر نمیکند و معکوس کسر را نیز لزوما صحیح نمیکند. هر دو عمل باعث منفی شدن مقدار عدد نمیشوند، بلکه هرکدام تغییر خاصی ایجاد میکنند که در تغییر علامت یا جابجایی اجزا است.
۷. با استفاده از قدر مطلق (absolute value)، برای محاسبه فاصله یک عدد تا قرینهاش روی محور اعداد، کدام روش صحیح است؟
عدد را با قرینهاش جمع میکنیم و قدر مطلق میگیریم.
قدر مطلق قرینه را از قدر مطلق عدد کم میکنیم.
عدد را تقسیم بر قدر مطلق آن میکنیم.
قدر مطلق عدد را در ۲ ضرب میکنیم.
برای محاسبه فاصله بین یک عدد و قرینهاش روی محور، باید قدر مطلق عدد را در ۲ ضرب کنیم، زیرا فاصله هر عدد تا نقطه مقابل خود روی محور دقیقا دو برابر فاصله آن از صفر است. استفاده از کم کردن قدر مطلقها درست نیست، زیرا هر دو نتیجه مشابه میدهند. جمع عدد و قرینه همیشه صفر میشود و قدر مطلق آن نیز صفر است که نشاندهنده فاصله نیست. اگر عدد را بر قدر مطلقش تقسیم کنیم، نتیجه فقط علامت را نشان میدهد و هیچ ارتباطی به فاصله ندارد.
۸. اگر یک عدد را دوبار قرینه کنیم، چه نتیجهای حاصل میشود و علت آن چیست؟
قرینه معکوس عدد به دست میآید، چون دو عمل مختلف انجام شده است.
عدد اولیه دوباره به دست میآید، چون تغییر علامت دوبار انجام شده است.
یک عدد منفی حاصل میشود، زیرا هر بار علامت تغییر میکند.
عدد صفر به دست میآید، چون قرینه قرینه همیشه برابر صفر است.
وقتی یک عدد را دوبار قرینه کنیم، در واقع دو بار عملیات ضرب در عدد منفی یک (۱-) انجام میشود. در بار اول عدد قرینه میشود و با بار دوم، علامت دوباره تغییر کرده و به حالت اولیه بازمیگردد. به همین دلیل نتیجه «عدد اولیه دوباره به دست میآید، چون تغییر علامت دوبار انجام شده است» صحیح است.













سلام روز بخیر. آیا اعداد قرینه متمایز هستن؟ مثلا اعداد 2 و -2 قرینه هستن ولی آیا متمایز هم محسوب میشن؟