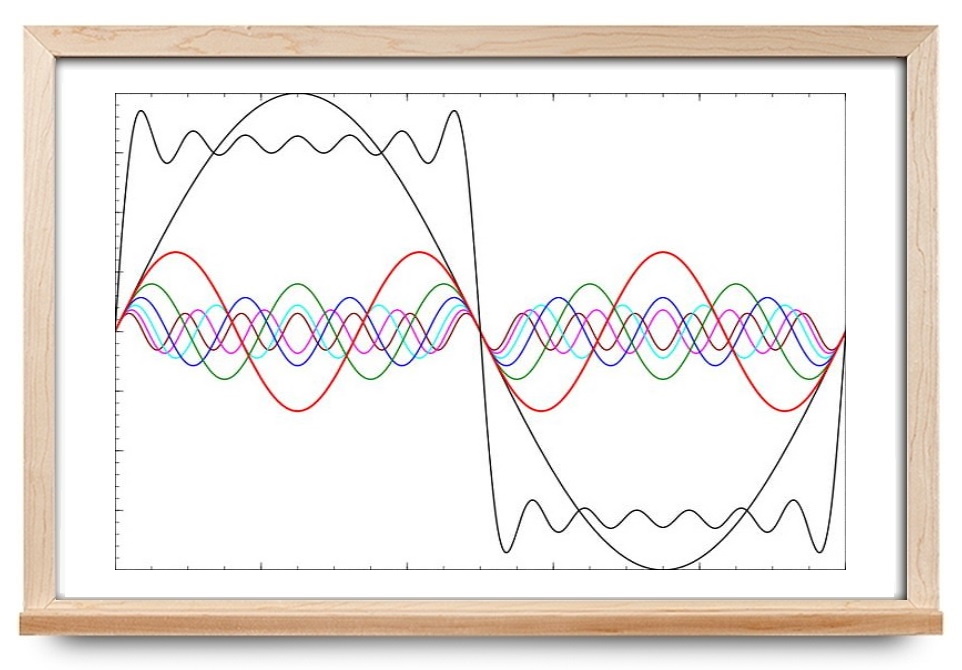
در آموزشهای قبلی مجله فرادرس، تعریف سری فوریه و مباحثی مانند سری فوریه مختلط ، سری فوریه سینوسی ، سری فوریه کسینوسی و همگرایی سری فوریه را بیان کردیم. در این آموزش، با نوشتن سری فوریه توابع متناوب با دوره تناوب دلخواه آشنا میشویم.
سری فوریه توابع متناوب روی بازه [ – L , L ] \Large \left[ { – L,L} \right] [ – L , L ]
فرض میکنیم که تابع f ( x ) f(x) f ( x ) [ – L , L ] \left[ { – L,L} \right] [ – L , L ] پیوسته باشد. با جایگذاری x = L y π x={\large\frac{{Ly}}{\pi }\normalsize} x = π L y – π ≤ x ≤ π { – \pi \le x \le \pi } – π ≤ x ≤ π
F ( y ) = f ( L y π ) \large F \left ( y \right ) = f \left ( { \frac { { L y } } { \pi } } \right ) F ( y ) = f ( π L y )
این تابع روی بازه [ – π , π ] \left[ { – \pi ,\pi } \right] [ – π , π ] F ( y ) F(y) F ( y )
F ( y ) = f ( L y π ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n y + b n sin n y ) . \large { F \left ( y \right ) = f \left ( { \frac { { L y } } { \pi } } \right ) } = { \frac { { { a _ 0 } } } { 2 } } + { \sum \limits _ { n = 1 } ^ \infty { \left ( { { a _ n } \cos n y + { b _ n } \sin n y } \right ) } . } F ( y ) = f ( π L y ) = 2 a 0 + n = 1 ∑ ∞ ( a n cos n y + b n sin n y ) .
ضرایب فوریه این تابع از روابط زیر به دست میآیند:
a 0 = 1 π ∫ – π π F ( y ) d y , a n = 1 π ∫ – π π F ( y ) cos n y d y = 1 π ∫ – π π f ( L y π ) cos n y d y , b n = 1 π ∫ – π π F ( y ) sin n y d y = 1 π ∫ – π π f ( L y π ) sin n y d y , n = 1 , 2 , 3 , … \large \begin {align*} { a _ 0 } & = \frac { 1 } { \pi } \int \limits _ { – \pi } ^ \pi { F \left ( y \right ) d y } , \\ { a _ n } & = \frac { 1 } { \pi } \int \limits _ { – \pi } ^ \pi { F \left ( y \right ) \cos n y d y } = { \frac { 1 } { \pi } \int \limits _ { – \pi } ^ \pi { f \left ( { \frac { { L y } } { \pi } } \right ) \cos n y d y } , } \\ { b _ n } & = \frac { 1 } { \pi } \int \limits _ { – \pi } ^ \pi { F \left ( y \right ) \sin n y d y } = { \frac { 1 } { \pi } \int \limits _ { – \pi } ^ \pi { f \left ( { \frac { { L y } } { \pi } } \right ) \sin n y d y } , \; \; } \kern-0.3pt { n = 1 , 2 , 3 , \ldots } \end {align*} a 0 a n b n = π 1 – π ∫ π F ( y ) d y , = π 1 – π ∫ π F ( y ) cos n y d y = π 1 – π ∫ π f ( π L y ) cos n y d y , = π 1 – π ∫ π F ( y ) sin n y d y = π 1 – π ∫ π f ( π L y ) sin n y d y , n = 1 , 2 , 3 , …
با بازگشت به متغیرهای اولیه و قرار دادن y = π x L y = {\large\frac{{\pi x}}{L}\normalsize} y = L π x f ( x ) f(x) f ( x )
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n π x L + b n sin n π x L ) \large { f \left ( x \right ) = \frac { { { a _ 0 } } } { 2 } \text { + }} \kern0pt{ \sum \limits _ { n = 1 } ^ \infty { \left ( { { a _ n } \cos \frac { { n \pi x } } { L } + { b _ n } \sin \frac { { n \pi x } } { L } } \right ) } } f ( x ) = 2 a 0 + n = 1 ∑ ∞ ( a n cos L nπ x + b n sin L nπ x )
که در آن:
a 0 = 1 L ∫ – L L f ( x ) d x , a n = 1 L ∫ – L L f ( x ) cos n π x L d x , b n = 1 L ∫ – L L f ( x ) sin n π x L d x . \large \begin {align*} { { a _ 0 } } & = { \frac { 1 } { L } \int \limits _ { – L } ^ L { f \left ( x \right ) d x } , \; \; }\kern-0.3pt \\ { { a _ n } } & = { \frac { 1 } { L } \int \limits _ { – L } ^ L { f \left ( x \right ) \cos \frac { { n \pi x } } { L } d x } , \; \; } \kern-0.3pt \\ { { b _ n } } & = { \frac { 1 } {L } \int \limits _ { – L } ^ L { f \left ( x \right ) \sin \frac { { n \pi x } } { L } d x } . } \end {align*} a 0 a n b n = L 1 – L ∫ L f ( x ) d x , = L 1 – L ∫ L f ( x ) cos L nπ x d x , = L 1 – L ∫ L f ( x ) sin L nπ x d x .
سری فوریه روی بازه [ a , b ] \Large \left[ { a,b} \right] [ a , b ]
اگر تابع f ( x ) f(x) f ( x ) [ a , b ] \left[ { a,b} \right] [ a , b ]
f ( x ) = a 0 2 + ∑ n = 1 ∞ ( a n cos n π x L + b n sin n π x L ) \large { f \left ( x \right ) = \frac { { { a _ 0 } } } { 2 } \text { + } } \kern0pt { \sum \limits _ { n = 1 } ^ \infty { \left ( { { a _ n } \cos \frac { { n \pi x } } { L } + { b _ n } \sin \frac { { n \pi x } } { L } } \right ) } } f ( x ) = 2 a 0 + n = 1 ∑ ∞ ( a n cos L nπ x + b n sin L nπ x )
در اینجا L = b – a 2 L = \large\frac{{b – a}}{2}\normalsize L = 2 b – a
a 0 = 2 L ∫ 0 L f ( x ) d x , a n = 2 L ∫ 0 L f ( x ) cos n π x L d x . \large { { a _ 0 } = \frac { 2 } { L } \int \limits _ 0 ^ L { f \left ( x \right ) d x } , \; \; } \kern-0.3pt { { a _ n } = \frac { 2 } { L } \int \limits _ 0 ^ L { f \left ( x \right ) \cos \frac { { n \pi x } } { L } d x } . } a 0 = L 2 0 ∫ L f ( x ) d x , a n = L 2 0 ∫ L f ( x ) cos L nπ x d x .
سری فوریه توابع زوج و فرد
بسط سری فوریه یک تابع زوج که روی بازه [ – L , L ] \left[ { – L,L} \right] [ – L , L ]
f ( x ) = a 0 2 + ∑ n = 1 ∞ a n cos n π x L , \large {f\left( x \right) }={ \frac{{{a_0}}}{2} + \sum\limits_{n = 1}^\infty {{a_n}\cos \frac{{n\pi x}}{L}} ,} f ( x ) = 2 a 0 + n = 1 ∑ ∞ a n cos L nπ x ,
که در آن:
a 0 = 2 L ∫ 0 L f ( x ) d x , a n = 2 L ∫ 0 L f ( x ) cos n π x L d x . \large {{a_0} = \frac{2}{L}\int\limits_0^L {f\left( x \right)dx} ,\;\;}\kern-0.3pt {{a_n} = \frac{2}{L}\int\limits_0^L {f\left( x \right)\cos \frac{{n\pi x}}{L}dx}.} a 0 = L 2 0 ∫ L f ( x ) d x , a n = L 2 0 ∫ L f ( x ) cos L nπ x d x .
بسط سری فوریه یک تابع فرد که روی بازه [ – L , L ] \left[ { – L,L} \right] [ – L , L ]
f ( x ) = ∑ n = 1 ∞ b n sin n π x L , \large f \left ( x \right ) = \sum \limits _ { n = 1 } ^ \infty { { b _ n } \sin \frac { { n \pi x } } { L } } , f ( x ) = n = 1 ∑ ∞ b n sin L nπ x ,
که در آن:
b n = 2 L ∫ 0 L f ( x ) sin n π x L d x . \large { { b _ n } } = { \frac { 2 } { L } \int \limits _ 0 ^ L { f \left ( x \right ) \sin \frac { { n \pi x } } { L } d x } . } b n = L 2 0 ∫ L f ( x ) sin L nπ x d x .
مثالها
در این بخش، چند مثال را بررسی میکنیم.
مثال ۱
سری فوریه تابع زیر را بیابید.
f ( x ) = { A , 0 ≤ x ≤ L 0 , L < x ≤ 2 L . \large { f \left ( x \right ) } = { \begin {cases} A , & 0 \le x \le L \\ 0, & L \lt x \le 2 L \end {cases}.} f ( x ) = ⎩ ⎨ ⎧ A , 0 , 0 ≤ x ≤ L L < x ≤ 2 L .
حل: ابتدا ضرایب فوریه را تعیین میکنیم:
a 0 = 1 L ∫ a b f ( x ) d x = 1 L ∫ 0 L A d x = A , \large { { a _ 0 } } = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) d x } } = { \frac { 1 } { L } \int \limits _ 0 ^ L { A d x } } = { A , } a 0 = L 1 a ∫ b f ( x ) d x = L 1 0 ∫ L A d x = A ,
a n = 1 L ∫ a b f ( x ) cos n π x L d x = 1 L ∫ a b A cos n π x L d x = A L [ ( L n π sin n π x L ) ∣ 0 L ] = A n π ( sin n π – sin 0 ) = 0 , \large \begin{align*} { { a _ n } } & = { \frac { 1 }{ L } \int \limits _ a ^ b { f \left ( x \right ) \cos \frac { { n \pi x } } { L } d x} } = { \frac { 1 } { L } \int \limits _ a ^ b { A \cos \frac { { n \pi x } } { L } d x } } \\ & = { \frac { A } { L } \left [ { \left . { \left ( { \frac { L } { { n \pi } } \sin \frac { { n \pi x } } { L } } \right ) } \right | _ 0 ^ L } \right ] } = { \frac { A } { { n \pi } } \left ( { \sin n \pi – \sin 0 } \right ) } = { 0 , } \end {align*} a n = L 1 a ∫ b f ( x ) cos L nπ x d x = L 1 a ∫ b A cos L nπ x d x = L A ( nπ L sin L nπ x ) 0 L = nπ A ( sin nπ – sin 0 ) = 0 ,
b n = 1 L ∫ a b f ( x ) sin n π x L d x = 1 L ∫ a b A sin n π x L d x = A L [ ( – L n π cos n π x L ) ∣ 0 L ] = A n π [ – cos n π + cos 0 ] = A n π [ 1 – ( – 1 ) n ] = A n π [ 1 + ( – 1 ) n + 1 ] . \large \begin{align*} { { b _ n } } & = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) \sin \frac { { n \pi x } } { L } d x } } = { \frac { 1 } { L } \int \limits _ a ^ b { A \sin \frac { { n \pi x } } { L } d x } } = { \frac { A } { L } \left [ { \left . { \left ( { – \frac { L } { { n \pi } } \cos \frac { { n \pi x } } { L } } \right ) } \right | _ 0 ^ L } \right ] } \\ & = { \frac { A } { { n \pi } } \left [ { – \cos n \pi + \cos 0 } \right] } = { \frac { A } { { n \pi } } \left [ { 1 – { { \left ( { – 1 } \right ) } ^ n } } \right ] } = { \frac { A} { { n \pi } } \left [ { 1 + { { \left ( { – 1 } \right ) } ^ { n + 1 } } } \right ] . } \end {align*} b n = L 1 a ∫ b f ( x ) sin L nπ x d x = L 1 a ∫ b A sin L nπ x d x = L A ( – nπ L cos L nπ x ) 0 L = nπ A [ – cos nπ + cos 0 ] = nπ A [ 1– ( –1 ) n ] = nπ A [ 1 + ( –1 ) n + 1 ] .
در صورتی که n = 2 k n = 2k n = 2 k k = 1 , 2 , 3 , … k = 1,2,3, \ldots k = 1 , 2 , 3 , …
b 2 k = A 2 k π [ 1 + ( – 1 ) 2 k + 1 ] = 0. \large { { b _ { 2 k } } } = { \frac { A } { { 2 k \pi } } \left [ { 1 + { { \left ( { – 1 } \right ) } ^ { 2 k + 1 } } } \right ] } = { 0 . } b 2 k = 2 kπ A [ 1 + ( –1 ) 2 k + 1 ] = 0.
برای n = 2 k − 1 n = 2k-1 n = 2 k − 1 k = 1 , 2 , 3 , … k = 1,2,3, \ldots k = 1 , 2 , 3 , …
b 2 k – 1 = A ( 2 k – 1 ) π [ 1 + ( – 1 ) 2 k ] = 2 A ( 2 k – 1 ) π . \large { { b _ { 2 k – 1 } } } = { \frac { A } { { \left ( { 2 k – 1 } \right ) \pi } } \left [ { 1 + { { \left ( { – 1 } \right ) } ^ { 2 k } } } \right ] } = { \frac { { 2 A } } { { \left ( { 2 k – 1 } \right ) \pi } } . } b 2 k –1 = ( 2 k –1 ) π A [ 1 + ( –1 ) 2 k ] = ( 2 k –1 ) π 2 A .
بنابراین، بسط سری فوریه این تابع برابر است با:
f ( x ) = A 2 + 2 A π ∑ k = 1 ∞ 1 2 k – 1 sin ( 2 k – 1 L π x ) \large { f \left ( x \right ) = \frac { A } { 2 } \text { + }}\kern0pt { \frac { { 2 A } } { \pi } \sum \limits _ { k = 1 } ^ \infty { \frac { 1 } { { 2 k – 1 } } \sin \left ( { \frac { { 2 k – 1 } } { L } \pi x } \right ) } } f ( x ) = 2 A + π 2 A k = 1 ∑ ∞ 2 k –1 1 sin ( L 2 k –1 π x )
مثال ۲
سری فوریه تابع زیر را به دست آورید.
f ( x ) = { 0 , − 1 ≤ x ≤ 0 x , 0 < x ≤ 1 . \large { f \left ( x \right ) } = { \begin {cases} 0 , & - 1 \le x \le 0 \\ x , & 0 \lt x \le 1 \end {cases} . } f ( x ) = ⎩ ⎨ ⎧ 0 , x , − 1 ≤ x ≤ 0 0 < x ≤ 1 .
حل: در اینجا L = 1 L=1 L = 1
a 0 = 1 L ∫ a b f ( x ) d x = ∫ – 1 1 f ( x ) d x = ∫ 0 1 x d x = ( x 2 2 ) ∣ 0 1 = 1 2 . \large { { a _ 0 } } = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) d x } } = { \int \limits _ { – 1 } ^ 1 { f \left ( x \right ) d x } } = { \int \limits _ 0 ^ 1 { x d x } } = { \left . { \left ( { \frac { { { x ^ 2 } } } { 2 } } \right ) } \right | _ 0 ^ 1 } = { \frac { 1 } { 2 } . } a 0 = L 1 a ∫ b f ( x ) d x = –1 ∫ 1 f ( x ) d x = 0 ∫ 1 x d x = ( 2 x 2 ) 0 1 = 2 1 .
اکنون ضرایب a n a_n a n b n b_n b n
a n = 1 L ∫ a b f ( x ) cos n π x L d x = ∫ 0 1 x cos ( n π x ) d x = ( 1 n π x sin ( n π x ) ) ∣ 0 1 − 1 n π ∫ 0 1 sin ( n π x ) d x = 1 n π [ ( x sin n π x ) ∣ 0 1 + ( cos n π x n π ) ∣ 0 1 ] = 1 n π [ sin n π + cos n π n π – 1 n π ] = 1 n 2 π 2 [ cos n π – 1 ] = 1 n 2 π 2 [ ( – 1 ) n – 1 ] . \large \begin {align*} { { a _ n } } & = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) \cos \frac { { n \pi x } } { L } d x } } = { \int \limits _ 0 ^ 1 { x \cos \left ( { n \pi x } \right ) d x } } \\ & = { \left . { \left ( { \frac { 1 } { { n \pi } } x \sin \left ( { n \pi x } \right ) } \right ) } \right | _ 0 ^ 1 } - { \frac { 1 } { { n \pi } } \int \limits _ 0 ^ 1 { \sin \left ( { n \pi x } \right ) d x } } \\ & = { { \frac { 1 } { { n \pi } } \left [ { \left . { \left ( { x \sin n \pi x } \right ) } \right | _ 0 ^ 1 } \right . } + { \left . { \left . { \left ( { \frac { { \cos n \pi x } } { { n \pi } } } \right ) } \right | _ 0 ^ 1 } \right ] } } \\ & = { \frac { 1 } { { n \pi } } \left [ { \sin n \pi + \frac { { \cos n \pi } } { { n \pi } } – \frac { 1 } { { n \pi } } } \right ] } = { \frac { 1 } { { { n ^ 2 } { \pi ^ 2 } } } \left [ { \cos n \pi – 1 } \right ] } \\ &= { \frac { 1 } { { { n ^ 2 } { \pi ^ 2 } } } \left [ { { { \left ( { – 1 } \right ) } ^ n } – 1 } \right ] . } \end {align*} a n = L 1 a ∫ b f ( x ) cos L nπ x d x = 0 ∫ 1 x cos ( nπ x ) d x = ( nπ 1 x sin ( nπ x ) ) 0 1 − nπ 1 0 ∫ 1 sin ( nπ x ) d x = nπ 1 [ ( x sin nπ x ) ∣ 0 1 + ( nπ cos nπ x ) 0 1 ] = nπ 1 [ sin nπ + nπ cos nπ – nπ 1 ] = n 2 π 2 1 [ cos nπ –1 ] = n 2 π 2 1 [ ( –1 ) n –1 ] .
b n = 1 L ∫ a b f ( x ) sin n π x L d x = ∫ 0 1 x sin ( n π x ) d x = ( – 1 n π x cos ( n π x ) ) ∣ 0 1 + 1 n π ∫ 0 1 cos ( n π x ) d x = 1 n π [ – ( x cos n π x ) ∣ 0 1 + ( sin n π x n π ) ∣ 0 1 ] = 1 n π [ – cos n π + sin n π n π ] = ( – 1 ) n + 1 n π . \large \begin {align*} { { b _ n } } & = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) \sin \frac { { n \pi x } }{ L } d x } } = { \int \limits _ 0 ^ 1 { x \sin \left ( { n \pi x } \right ) d x } } \\ & = { \left . { \left ( { – \frac { 1 } { { n \pi } } x \cos \left ( { n \pi x } \right ) } \right ) } \right | _ 0 ^ 1 } + { \frac { 1 } { { n \pi } } \int \limits _ 0 ^ 1 { \cos \left ( { n \pi x } \right ) d x } } \\ & = { { \frac { 1 } { { n \pi } } \left [ { \left . { – \left ( { x \cos n \pi x } \right ) } \right | _ 0 ^ 1 } \right . } + { \left . { \left . { \left ( { \frac { { \sin n \pi x } } { { n \pi } } } \right ) } \right | _ 0 ^ 1 } \right ] } } \\ & = { \frac { 1 } { { n \pi } } \left [ { – \cos n \pi + \frac { { \sin n \pi } } { { n \pi } } } \right ] } = { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } }} { { n \pi } } . } \end {align*} b n = L 1 a ∫ b f ( x ) sin L nπ x d x = 0 ∫ 1 x sin ( nπ x ) d x = ( – nπ 1 x cos ( nπ x ) ) 0 1 + nπ 1 0 ∫ 1 cos ( nπ x ) d x = nπ 1 [ – ( x cos nπ x ) ∣ 0 1 + ( nπ sin nπ x ) 0 1 ] = nπ 1 [ – cos nπ + nπ sin nπ ] = nπ ( –1 ) n + 1 .
در نتیجه، داریم:
f ( x ) = 1 4 + ∑ n = 1 ∞ [ ( ( – 1 ) n – 1 ) n 2 π 2 cos n π x + ( – 1 ) n + 1 n π sin n π x ] . \large { f \left ( x \right ) = \frac { 1 } { 4 } } + { \sum \limits _ { n = 1 } ^ \infty { \left [ { \frac { { \left ( { { { \left ( { – 1 } \right ) } ^ n } – 1 } \right ) } } { { { n ^ 2 } { \pi ^ 2 } } } \cos n \pi x } \right . } } + { { \left . { \frac { { { { \left ( { – 1 } \right ) } ^ { n + 1 } } } } { { n \pi } } \sin n \pi x } \right ] } . } f ( x ) = 4 1 + n = 1 ∑ ∞ [ n 2 π 2 ( ( –1 ) n –1 ) cos nπ x + nπ ( –1 ) n + 1 sin nπ x ] .
مثال ۳
سری فوریه موج ذوزنقهای زیر را بیابید.
f ( x ) = { x , 0 ≤ x ≤ 1 1 , 1 < x ≤ 2 3 − x , 2 < x ≤ 3 . \large { f \left ( x \right ) } = { \begin {cases} x , & 0 \le x \le 1 \\ 1 , & 1 \lt x \le 2 \\ 3 - x , & 2 \lt x \le 3 \end {cases} . } f ( x ) = ⎩ ⎨ ⎧ x , 1 , 3 − x , 0 ≤ x ≤ 1 1 < x ≤ 2 2 < x ≤ 3 .
حل: بدیهی است که L = 3 2 L = {\large\frac{3}{2}\normalsize} L = 2 3 a 0 a_0 a 0 a n a_n a n
a 0 = 1 L ∫ a b f ( x ) d x = 2 3 ∫ 0 3 f ( x ) d x = 2 3 [ ∫ 0 1 x d x + ∫ 1 2 1 d x + ∫ 2 3 ( 3 – x ) d x ] = 2 3 [ ( x 2 2 ) ∣ 0 1 + x ∣ 0 1 + ( 3 x – x 2 2 ) ∣ 2 3 ] = 4 3 ; \large \begin {align*} { { a _ 0 } } & = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) d x } } = { \frac { 2 } { 3 } \int \limits _ 0 ^ 3 { f \left ( x \right ) d x } } \\ &= { { \frac { 2 } { 3 } \left [ { \int \limits _ 0 ^ 1 { x d x } + \int \limits _ 1 ^ 2 { 1 d x } } \right . } + { \left . { \int \limits _ 2 ^ 3 { \left ( { 3 – x } \right ) d x } } \right ] } } \\ & = { { \frac { 2 } { 3 } \left [ { \left . { \left ( { \frac { { { x ^ 2 } } } { 2 } } \right ) } \right | _ 0 ^ 1 + \left . x \right | _ 0 ^ 1 } \right . } } + { { \left . { \left . { \left ( { 3 x – \frac { { { x ^ 2 } } } { 2 } } \right ) } \right | _ 2 ^ 3 } \right ] } } = { \frac { 4 }{ 3 } ; } \end {align*} a 0 = L 1 a ∫ b f ( x ) d x = 3 2 0 ∫ 3 f ( x ) d x = 3 2 0 ∫ 1 x d x + 1 ∫ 2 1 d x + 2 ∫ 3 ( 3– x ) d x = 3 2 ( 2 x 2 ) 0 1 + x ∣ 0 1 + ( 3 x – 2 x 2 ) 2 3 = 3 4 ;
a n = 1 L ∫ a b f ( x ) cos n π x L d x = 2 3 ∫ 0 3 f ( x ) cos 2 n π x 3 d x = 2 3 { ∫ 0 1 x cos 2 n π x 3 d x + ∫ 1 2 cos 2 n π x 3 d x + ∫ 2 3 ( 3 – x ) cos 2 n π x 3 d x } = 2 3 { [ ( 3 2 n π x sin 2 n π x 3 ) ∣ 0 1 − ∫ 0 1 3 2 n π sin 2 n π x 3 d x ] + ( 3 2 n π sin 2 n π x 3 ) ∣ 1 2 + [ ( 3 2 n π ( 3 – x ) sin 2 n π x 3 ) ∣ 2 3 + ∫ 2 3 3 2 n π sin 2 n π x 3 d x ] } = 2 3 { 3 2 n π sin 2 n π 3 + 9 4 n 2 π 2 ( cos 2 n π 3 – 1 ) + 3 2 n π ( sin 4 n π 3 – sin 2 n π 3 ) – 3 2 n π sin 4 n π 3 + 9 4 n 2 π 2 ( - cos 2 n π + cos 4 n π 3 ) } = 2 3 { 9 4 n 2 π 2 ( cos 2 n π 3 – 1 ) + 9 4 n 2 π 2 ( cos 4 n π 3 – 1 ) } . \large \begin {align*} { { a _ n } } & = { \frac { 1 } { L } \int \limits _ a ^ b { f \left ( x \right ) \cos \frac { { n \pi x } }{ L } d x } } = { \frac { 2 } { 3 } \int \limits _ 0 ^ 3 { f \left ( x \right ) \cos \frac { { 2 n \pi x } } { 3 } d x } } \\ & = { \frac { 2 } { 3 } \left\{ { \int \limits _ 0 ^ 1 { x \cos \frac { { 2 n \pi x } } { 3 } d x } } \right . } + { \int \limits _ 1 ^ 2 { \cos \frac { { 2 n \pi x } } { 3 } d x } } + { \left . { \int \limits _ 2 ^ 3 { \left ( { 3 – x } \right ) \cos \frac { { 2 n \pi x } } { 3 } d x } } \right\} } \\ & = { \frac { 2 } { 3 }\left\{ {\left[ {\left. {\left( {\frac{3}{ { 2 n \pi } } x \sin \frac { { 2 n \pi x } } { 3 } } \right ) } \right | _ 0 ^ 1 } \right . } \right . } - { \left . { \left . { \int \limits _ 0 ^ 1 { \frac { 3 } { { 2 n \pi } } \sin \frac { { 2 n \pi x } } { 3 } d x } } \right ] } \right . } \\ & + { \left . { \left ( { \frac { 3 } { { 2 n \pi } } \sin \frac { { 2 n \pi x } } { 3 } } \right ) } \right | _ 1 ^ 2 } + { \left . { \left [ { \left . { \left ( { \frac { 3 } { { 2 n \pi } } \left ( { 3 – x } \right ) \sin \frac { { 2 n \pi x } } { 3 } } \right ) } \right | _ 2 ^ 3 } \right . } \right . } + { \left . { \left . { \int \limits _ 2 ^ 3 { \frac { 3 } { { 2 n \pi } } \sin \frac { { 2 n \pi x } } {3 } d x } } \right ] } \right\} } \\ & = { \frac { 2 } { 3 } \left\{ { \frac { 3 } { { 2 n \pi } } \sin \frac { { 2 n \pi } } {3 } } \right . } + { \frac { 9 } { { 4 { n ^ 2 } { \pi ^ 2 } } } \left ( { \cos \frac { { 2 n \pi } } { 3 } – 1 } \right ) } + { \frac { 3 } { { 2 n \pi } } \left ( { \sin \frac { { 4 n \pi } } { 3 } – \sin \frac { { 2 n \pi } } { 3 } } \right ) } – { \frac { 3 } { { 2 n \pi } } \sin \frac { { 4 n \pi } } { 3 } } \\ &+ { \left . { \frac { 9 } { { 4 { n ^ 2 } { \pi ^ 2 } } } \left ( { \text{-} \cos 2 n \pi + \cos \frac { { 4 n \pi } } { 3 } } \right ) } \right \} } = { \frac { 2 } { 3 } \left\{ { \frac { 9 } { { 4 { n ^ 2 } { \pi ^ 2 } } } \left ( { \cos \frac { { 2 n \pi } } { 3 } – 1 } \right ) } \right . } + { \left . { \frac { 9 } { { 4 { n ^ 2 } { \pi ^ 2 } } } \left ( { \cos \frac { { 4 n \pi } } { 3 } – 1 } \right ) } \right \} . } \end {align*} a n = L 1 a ∫ b f ( x ) cos L nπ x d x = 3 2 0 ∫ 3 f ( x ) cos 3 2 nπ x d x = 3 2 ⎩ ⎨ ⎧ 0 ∫ 1 x cos 3 2 nπ x d x + 1 ∫ 2 cos 3 2 nπ x d x + 2 ∫ 3 ( 3– x ) cos 3 2 nπ x d x ⎭ ⎬ ⎫ = 3 2 { [ ( 2 nπ 3 x sin 3 2 nπ x ) 0 1 − 0 ∫ 1 2 nπ 3 sin 3 2 nπ x d x + ( 2 nπ 3 sin 3 2 nπ x ) 1 2 + [ ( 2 nπ 3 ( 3– x ) sin 3 2 nπ x ) 2 3 + 2 ∫ 3 2 nπ 3 sin 3 2 nπ x d x ⎭ ⎬ ⎫ = 3 2 { 2 nπ 3 sin 3 2 nπ + 4 n 2 π 2 9 ( cos 3 2 nπ –1 ) + 2 nπ 3 ( sin 3 4 nπ – sin 3 2 nπ ) – 2 nπ 3 sin 3 4 nπ + 4 n 2 π 2 9 ( - cos 2 nπ + cos 3 4 nπ ) } = 3 2 { 4 n 2 π 2 9 ( cos 3 2 nπ –1 ) + 4 n 2 π 2 9 ( cos 3 4 nπ –1 ) } .
از آنجایی که cos 4 n π 3 = cos ( 2 n π – 2 n π 3 ) = cos 2 n π 3 \cos {\large\frac{{4n\pi }}{3}\normalsize} = \cos \left( {2n\pi – {\large\frac{{2n\pi }}{3}\normalsize}} \right) = \cos {\large\frac{{2n\pi }}{3}\normalsize} cos 3 4 nπ = cos ( 2 nπ – 3 2 nπ ) = cos 3 2 nπ
a n = 2 3 ⋅ 2 ⋅ 9 4 n 2 π 2 ( cos 2 n π 3 – 1 ) = 3 n 2 π 2 ( cos 2 n π 3 – 1 ) , n = 1 , 2 , 3 , … \large { { a _ n } } = { \frac { 2 } { 3 } \cdot \frac { { 2 \cdot 9 } } { { 4 { n ^ 2 } { \pi ^ 2 } } } \left ( { \cos \frac { { 2 n \pi } } { 3 } – 1 } \right ) } = { \frac { 3 } { { { n ^ 2 } { \pi ^ 2 } } } \left ( { \cos \frac { { 2 n \pi } } { 3 } – 1 } \right ) , \; \; } \kern-0.3pt { n = 1 , 2 , 3 , \ldots } a n = 3 2 ⋅ 4 n 2 π 2 2 ⋅ 9 ( cos 3 2 nπ –1 ) = n 2 π 2 3 ( cos 3 2 nπ –1 ) , n = 1 , 2 , 3 , …
ضرایب b n b_n b n [ 0 , 3 ] \left[ {0,3} \right] [ 0 , 3 ]
f ( x ) = 2 3 – 3 π 2 ⋅ ∑ n = 1 ∞ 1 – cos 2 n π 3 n 2 cos 2 n π x 3 \large { f \left ( x \right ) = \frac { 2 } { 3 } – \frac { 3 } { { { \pi ^ 2 } } } \cdot \kern0pt{ \sum \limits _ { n = 1 } ^ \infty { \frac { { 1 – \cos \frac { { 2 n \pi } } { 3} } } { { { n ^ 2 } }} \cos \frac { { 2 n \pi x } } { 3 } } } } f ( x ) = 3 2 – π 2 3 ⋅ n = 1 ∑ ∞ n 2 1– cos 3 2 nπ cos 3 2 nπ x
مثال ۴
سری فوریه تابع f ( x ) = cos 2 x f\left( x \right) = {\cos ^2}x f ( x ) = cos 2 x
حل: این تابع زوج بوده و دوره تناوب آن، π \pi π L = π 2 {L = {\large\frac{\pi }{2}\normalsize}} L = 2 π b n = 0 b_n=0 b n = 0 a 0 a_0 a 0 a n a_n a n
a 0 = 2 L ∫ 0 L f ( x ) d x = 4 π ∫ 0 π 2 cos 2 x d x = 2 π ∫ 0 π 2 ( 1 + cos 2 x ) d x = 2 π [ ( x + sin 2 x 2 ) ∣ 0 π 2 ] = 2 π [ π 2 + sin π 2 ] = 1. \large \begin {align*} { a _ 0 } & = \frac { 2 } { L } \int \limits _ 0 ^ L { f \left ( x \right ) d x } = { \frac { 4 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { { \cos } ^ 2 } x d x } } = { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \left ( { 1 + \cos 2 x } \right ) d x } } \\ & = { \frac { 2 } { \pi } \left[ { \left . { \left ( { x + \frac { { \sin 2 x } } { 2 } } \right ) } \right | _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } } \right ] } = { \frac { 2 } { \pi } \left [ { \frac { \pi } { 2 } + \frac { { \sin \pi } } { 2 } } \right ] } = { 1 . } \end {align*} a 0 = L 2 0 ∫ L f ( x ) d x = π 4 0 ∫ 2 π cos 2 x d x = π 2 0 ∫ 2 π ( 1 + cos 2 x ) d x = π 2 ( x + 2 sin 2 x ) 0 2 π = π 2 [ 2 π + 2 sin π ] = 1.
a n = 2 L ∫ 0 L f ( x ) cos n π x L d x = 4 π ∫ 0 π 2 cos 2 x cos 2 n x d x = 2 π ∫ 0 π 2 ( 1 + cos 2 x ) cos 2 n x d x = 2 π ∫ 0 π 2 ( cos 2 n x + cos 2 x cos 2 n x ) d x = 2 π ∫ 0 π 2 [ 2 cos 2 n x + cos ( 2 n – 2 ) x + cos ( 2 n + 2 ) x ] d x = 1 π [ sin 2 n x n + sin ( 2 n – 2 ) x 2 n – 2 + sin ( 2 n + 2 ) x 2 n + 2 ] ∣ 0 π 2 = 1 π [ sin n π n + sin ( n – 1 ) π 2 n – 2 + sin ( n + 1 ) π 2 n + 2 ] = 0. \large \begin{align*} { a _ n } & = \frac { 2 } { L } \int \limits _ 0 ^ L { f \left ( x \right ) \cos \frac { { n \pi x } } { L } d x } = { \frac { 4 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { { \cos } ^ 2 } x \cos 2 n x d x } } \\ & = { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize} { \left ( { 1 + \cos 2 x } \right ) \cos 2 n x d x } } \\ & = { { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \left ( { \cos 2 n x } \right . } + { \left . { \cos 2 x \cos 2 n x } \right ) d x } } } \\ & = { { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \left [ { 2 \cos 2 n x } \right . } + { \left . { \cos \left ( { 2 n – 2 } \right ) x } \right . } } } + { { { \left . { \cos \left ( { 2 n + 2 } \right ) x } \right ] d x } } } \\ & = { { \frac { 1 } { \pi } \left . { \left [ { \sin \frac { { 2 n x } } { n } } \right . } + { \left . { \sin \frac { { \left ( { 2 n – 2 } \right ) x } } { { 2 n – 2 } } } \right . } \right . } } + { { \left . { \left . { \sin \frac { { \left ( { 2 n + 2 } \right ) x } } { { 2 n + 2 } } } \right ] } \right | _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } } } \\ & = { { \frac { 1 } { \pi } \left [ { \frac { { \sin n \pi } } { n } } \right . } + { \left . { \frac { { \sin \left ( { n – 1 } \right ) \pi } } { { 2 n – 2 } } } \right . } } + { { \left . { \frac { { \sin \left ( { n + 1 } \right ) \pi } } { { 2 n + 2 } } } \right ] } } = { 0 . } \end {align*} a n = L 2 0 ∫ L f ( x ) cos L nπ x d x = π 4 0 ∫ 2 π cos 2 x cos 2 n x d x = π 2 0 ∫ 2 π ( 1 + cos 2 x ) cos 2 n x d x = π 2 0 ∫ 2 π ( cos 2 n x + cos 2 x cos 2 n x ) d x = π 2 0 ∫ 2 π [ 2 cos 2 n x + cos ( 2 n –2 ) x + cos ( 2 n + 2 ) x ] d x = π 1 [ sin n 2 n x + sin 2 n –2 ( 2 n –2 ) x + sin 2 n + 2 ( 2 n + 2 ) x ] 0 2 π = π 1 [ n sin nπ + 2 n –2 sin ( n –1 ) π + 2 n + 2 sin ( n + 1 ) π ] = 0.
اما این نتیجه فقط برای n ≥ 2 n \ge 2 n ≥ 2 a 1 a_1 a 1
a 1 = 4 π ∫ 0 π 2 cos 2 x cos 2 x d x = 2 π ∫ 0 π 2 ( 1 + cos 2 x ) cos 2 x d x = 2 π ∫ 0 π 2 ( cos 2 x + cos 2 2 x ) d x = 2 π ∫ 0 π 2 ( cos 2 x + 1 + cos 4 x 2 ) d x = 1 π ∫ 0 π 2 ( 2 cos 2 x + 1 + cos 4 x ) d x = 1 π [ ( sin 2 x + x + sin 4 x 4 ) ∣ 0 π 2 ] = 1 π ( sin π + π 2 + sin 2 π 4 ) = 1 2 . \large \begin {align*} { { a _ 1 } } & = { \frac { 4 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { { { \cos } ^ 2 } x \cos 2 x d x } } = { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \left ( { 1 + \cos 2 x } \right ) \cos 2 x d x } } \\ & = { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi } { 2 } \normalsize } { \left ( { \cos 2 x + { { \cos } ^ 2 } 2 x } \right ) d x } } = { \frac { 2 } { \pi } \int \limits _ 0 ^ { \large \frac { \pi }{ 2 } \normalsize } { \left ( { \cos 2 x + \frac { { 1 + \cos 4 x } } { 2 } } \right ) d x} } \\ & = {\frac{1}{\pi }\int\limits_0^{\large\frac{\pi }{2}\normalsize} {\left( {2\cos 2x + 1 + \cos 4x} \right)dx} } = {\frac{1}{\pi }\left[ {\left. {\left( {\sin 2x + x + \frac{{\sin 4x}}{4}} \right)} \right|_0^{\large\frac{\pi }{2}\normalsize}} \right] } \\ & = {\frac{1}{\pi }\left( {\sin \pi + \frac{\pi }{2} + \frac{{\sin 2\pi }}{4}} \right) } = {\frac{1}{2}.} \end {align*} a 1 = π 4 0 ∫ 2 π cos 2 x cos 2 x d x = π 2 0 ∫ 2 π ( 1 + cos 2 x ) cos 2 x d x = π 2 0 ∫ 2 π ( cos 2 x + cos 2 2 x ) d x = π 2 0 ∫ 2 π ( cos 2 x + 2 1 + cos 4 x ) d x = π 1 0 ∫ 2 π ( 2 cos 2 x + 1 + cos 4 x ) d x = π 1 ( sin 2 x + x + 4 sin 4 x ) 0 2 π = π 1 ( sin π + 2 π + 4 sin 2 π ) = 2 1 .
بدین ترتیب، سری فوریه تابع f ( x ) = = cos 2 x f\left( x \right)== {\cos ^2}x f ( x ) == cos 2 x
f ( x ) = cos 2 x = 1 2 + 1 2 cos 2 x . \large { f \left ( x \right ) = { \cos ^ 2 } x } = { \frac { 1 } { 2 } + \frac { 1 } { 2 } \cos 2 x . } f ( x ) = cos 2 x = 2 1 + 2 1 cos 2 x .
همانطور که میبینیم، سری به دست آمده همان اتحاد مثلثاتی معروف است.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^