دبی چیست؟ – به زبان ساده + نحوه محاسبه

سیالات (شاره‌ها) یا ساکن هستند یا حرکت می‌کنند. بررسی رفتار سیالات در هر دو حالت، به خصوص به هنگام حرکت آن‌ها در لوله، بسیار مهم است. دبی یکی از مفاهیمی است که به هنگام حرکت سیال به آن توجه می‌شود. به مقدار حجم آب یا هر مایعِ دلخواهی که از مقطعی مشخص در لوله در مدت زمان t جابجا می‌شود، دبی می‌گوییم. به هنگام بررسی دبی جریان، ویسکوزیته یا گرانروی آب را برابر صفر در نظر می‌گیریم. در این مطلب از مجله فرادرس، ابتدا به پرسش دبی چیست به زبان ساده پاسخ می‌دهیم. سپس دبی جرمی و معادله پیوستگی جریان را به‌دست می‌آوریم و در انتها، تعدادی مثال با یکدیگر حل می‌کنیم.

دبی چیست ؟

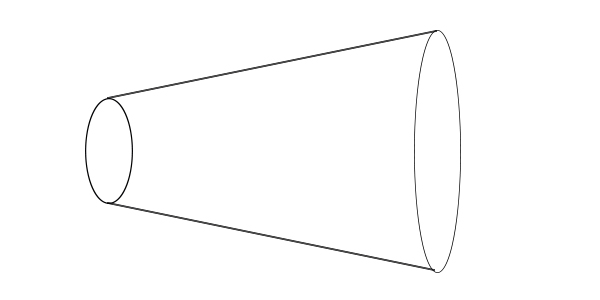
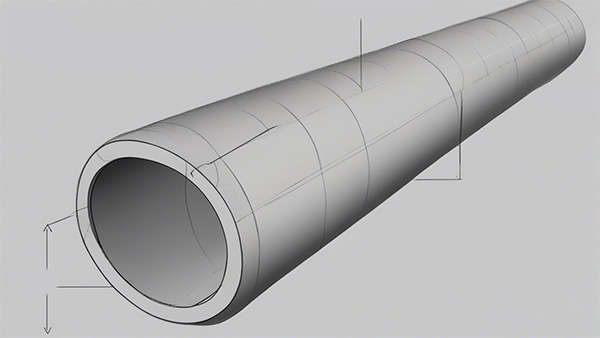
سیالات یا ساکن هستند یا حرکت می‌کنند. دبی در سیالات متحرک نقش مهمی را ایفا می‌کند. به مقدار حجم آب یا مایع جابجا شده از مقطعی مشخص در مدت زمان t، دبی گفته می‌شود. لوله‌ای فرضی را به صورت نشان داده شده در تصویر زیر در نظر بگیرید.

سطح مقطع این لوله با حرکت به سمت راست افزایش می‌یابد. این لوله با مایعی دلخواه، مانند آب، پر شده است. آب از سطح مقطع کوچک‌تر ($$ A_ { in }$$) وارد و از سطح مقطع بزرگ‌تر ($$ A _ { out }$$) خارج می‌شود. همان‌طور که در تصویر زیر مشاهده می‌کنید $$ A _ { out }$$ از $$ A_ { in }$$ بزرگ‌تر است. اگر مایعِ داخل لوله حرکت کند، چه اتفاقی رخ می‌دهد؟

فرض کنید مایع با سرعت $$ v _ { in }$$ به لوله وارد می‌شود. چه مقدار حجم پس از t ثانیه وارد لوله می‌شود؟ آب از سطح مقطع $$ A_ { in }$$ وارد لوله می‌شود. در مدت زمان t چه مسافتی را طی می‌کند؟ اگر جسمی با سرعت $$v$$ حرکت کند، مسافت طی شده توسط آن در مدت زمان t با استفاده از رابطه زیر به‌دست می‌آید:

$$d = vt$$

آب با سرعت $$ v _ { in }$$ وارد لوله می‌شود و پس از مدت زمان t مسافتی برابر $$ v _ { in } \times t$$ را طی می‌کند. فرض کنید قطر لوله در این مسافت مقدار زیادی تغییر نمی‌کند. همان‌طور که در تصویر زیر مشاهده می‌کنید حجم سبزرنگ از آب در مدت زمان t وارد لوله شده است.  حجم استوانه سبزرنگ حاوی آب چه مقدار است؟ حجم استوانه برابر حاصل‌ضرب سطح مقطع در طول آن است. در این مثال، سطح مقطع استوانه برابر $$A _ { in }$$ و طول آن برابر $$ v _ { in } \times t$$ است:

$$V_ { in } = A_ { in } \times ( v _ { in } . t )$$

توجه به این نکته مهم است که شاره‌ها، گاز یا مایع، تراکم‌ناپذیر هستند. به همین دلیل، حجم مایع وارد شده به لوله باید با حجم مایع خارج شده از لوله برابر باشد. در نتیجه، حجم مایع ورودی به لوله، $$V _ { in }$$، با حجم مایع خروجی از لوله، $$V _ { out }$$، برابر خواهد بود.. همچنین، فرض می‌کنیم که جریان آب داخل لوله کاملا روان و گرانروی و اصطکاک برابر صفر است.

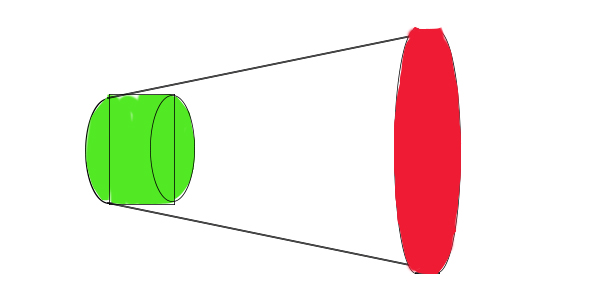
در ابتدای این بخش فهمیدیم دبی چیست. در ادامه، معادله مهمی به نام معادله پیوستگی را به‌دست می‌آوریم. سوال مهمی که ممکن است مطرح شود آن است که حجم آب خروجی از لوله چه مقدار است. حجم آب خروجی از لوله به شکل استوانه‌ای قرمزرنگ نشان داده شده است. سطح مقطع استوانه را برابر $$A_ { out }$$ در نظر گرفتیم. با توجه به آن‌که سرعت خروج آب از لوله برابر $$v_ { out}$$ است، مسافت طی شده توسط آب خروجی از لوله در مدت زمان t برابر $$v_ { out } \times t$$ خواهد بود. حجم آبِ ورودی به لوله برابر حجم آبِ خروجی از لوله است:

$$V _ { in} = V_ { out} \\ A_ { in } \times ( v_ { in } t ) = A_ { out}
\times ( v_ { out } t )$$

با حذف زمان از طرفین رابطه فوق به رابطه زیر می‌رسیم:

$$V _ { in} = V_ { out} \\ A_ { in } \times ( v_ { in } ) = A_ { out}
\times ( v_ { out } )$$

به معادله فوق در سیالات، معادله پیوستگی گفته می‌شود. سوال مهمی که در ادامه می‌خواهیم به آن پاسخ دهیم آن است که مقدار حجم بر ثانیه چیست. مقدار حجم جابجا شده بر ثانیه بسیار آشنا به نظر می‌رسد. به تعریف دبی در ابتدای این بخش مراجعه کنید. به مقدار حجم آب یا مایع جابجا شده از مقطعی مشخص در مدت زمان t، دبی می‌گوییم و آن را با Q نشان می‌دهیم. بنابراین، در ادامه رابطه ریاضی دبی را به‌دست می‌آوریم.

فرمول دبی چیست ؟

در بخش قبل فهمیدیم دبی چیست. در این بخش فرمول دبی را به‌دست می‌آوریم. واحد اندازه‌گیری دبی در سیستم SI، متر مکعب بر ثانیه یا $$\frac { m ^ 3 } { s}$$ است. دبی با استفاده از رابطه زیر به‌دست می‌آید:

$$\frac { V } { t }$$

همان‌طور که در مطالب بالا اشاره کردیم، حجم قسمتی از مایع درون لوله را می‌توانیم به صورت استوانه‌ای فرضی در نظر بگیریم. حجم استوانه برابر حاصل‌ضرب سطح مقطع در طول آن است و به صورت $$ V = A d$$ نوشته می‌شود. در این رابطه، A سطح مقطع استوانه و d طول آن است. با جایگذاری رابطه نوشته برای حجم در رابطه $$\frac { Q } { t }$$ داریم:

$$Q = \frac { V } { t } = \frac { A d } { t } = A \frac { d }  { t }$$

عبارت $$\frac { v} { t }$$ همان سرعت حرکت مایع در لوله است. بنابراین، Q را می‌توانیم به صورت زیر بنویسیم:

$$Q =Av $$

رابطه به‌دست آمده برای دبی بسیار آشناست. حاصل‌ضرب مساحت در سرعت را در معادله پیوستگی مشاهده کردید. از این رو، می‌توانیم بگوییم مقدار حجم مایع وارد شده به لوله در مدت زمان t برابر مقدار حجمِ مایع خارج شده از لوله در همین زمان است. A سطح مقطع بخشی از لوله و $$v$$ سرعت عبور مایع از آن بخش است. به این نکته توجه داشته باشید که از بین دو فرمول $$Q = \frac { V } { t } $$ و $$Q =Av $$ برای Q، رابطه $$Q =Av $$ فرمول مناسب‌تری برای حل مسائل است، زیرا محاسبه مساحت راحت‌تر خواهد بود. بیشتر لوله‌ها به شکل استوانه ساخته می‌شوند، بنابراین مساحت سطح مقطع آن‌ها برابر $$A = \pi r ^ 2$$ است.

تا اینجا می‌دانیم دبی جریان چیست و با استفاده از چه رابطه‌ای به‌دست می‌آید. همچنین، معادله پیوستگی را به‌دست آوردیم. بر طبق معادله پیوستگی، حجم وارد شده به لوله‌ای در مدت زمانی مشخص برابر حجم مایع خارج شده از لوله در همان زمان است. نرخ جریان شاره را با استفاده از نرخ جریان جرمی (دبی جرمی) نیز می‌توانیم توصیف کنیم. در ادامه، در مورد پایستگی جرم صحبت می‌کنیم.

واحد اندازه گیری دبی چیست ؟

واحد اندازه‌گیری دبی در سیستم SI، متر مکعب بر ثانیه است.

پایستگی جرم

در بخش‌های قبل فهمیدیم دبی چیست و با استفاده از چه فرمولی به‌دست می‌آید. در این بخش با مفهوم دیگری به نام دبی جرمی یا نرخ جرمی جریان آشنا می‌شویم. به مقدار جرم سیالِ عبوری از نقطه‌ای مشخص در واحد زمان، دبی جرمی یا نرخ جرمی جریان گفته می‌شود.

تصویر زیر را در نظر بگیرید. مقدار جرم سیال با حجم هاشورزده مشخص شده است. جرم را می‌توان با استفاده از چگالی و حجم به‌دست آورد:

$$m = \rho V = \rho A x $$

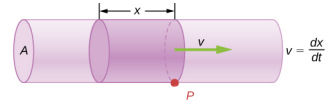
دبی جریان یا نرخ جریان جرمی، $$\frac{\text{d} m}{\text{d} t }$$ برابر است با:

$$\frac{\text{d} m}{\text{d} t }=
\frac{\text{d} }{\text{d} t } (\rho A x ) = \rho A
\frac{\text{d}x}{\text{d}t} = \rho A v$$

در رابطه فوق:

• $$\rho$$ چگالی سیال و واحد اندازه‌گیری آن کیلوگرم بر متر مکعب یا گرم بر سانتی‌متر مکعب است.
• $$A$$ سطح مقطع و واحد اندازه‌گیری آن متر مربع یا سانتی‌متر مربع است.
• $$v$$ سرعت حرکت سیال و واحد اندازه‌گیری آن متر بر ثانیه است.

دبی جریان کمیت بسیار مهمی در دینامیک سیالات است و با استفاده از آن می‌توانیم بسیاری از مسائل در زمینه سیالات را حل کنیم. به تصویر نشان داده شده در ادامه توجه کنید. شاره‌ای در لوله‌ای با دو سطح مقطع متفاوت جریان دارد. سطح مقطع لوله در ابتدای آن بزرگ‌تر از انتهای آن است.

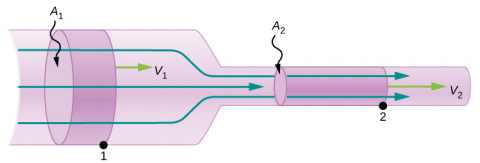
جرم شاره وارد شده به لوله باید برابر جرم شاره خارج شده از آن باشد. به همین دلیل، سرعت شاره به هنگام ورود به لوله، کوچک‌تر از سرعت آن به هنگام خروج از لوله است:

$$v_2 > v_1$$

با توجه به آن‌که جرم شاره وارد شده به لوله با جرم شاره خارج شده از آن برابر است، به راحتی می‌توانیم بین سطح مقطع و سرعت جریان شاره رابطه‌ای به صورت زیر به‌دست آوریم.

$$m_1 = m_2 \\
\frac{\text{d}m_1}{\text{d}t} =
\frac{\text{d}m_2}{\text{d}t} \\
\rho _ 1 A_1 v_ 1 = \rho_2 A_2 v_2 $$

به رابطه به‌دست آمده در بالا نیز، رابطه پیوستگی در حالت کلی گفته می‌شود. اگر جرم سیال در مدت انقباض ثابت بماند می‌توانیم آن را از طرفین رابطه به‌دست آمده حذف کنیم و به معادله پیوستگی به‌دست آمده در ابتدای مطلب برسیم. یکسان بودن چگالی سیال در سراسر لوله به معنای تراکم‌ناپذیری آن است.

$$A_ 1 v_1 = A_ 2 v_2$$

و بار دیگر فهمیدیم دبی جریان شاره ورودی به لوله برابر دبی جریان شاره خارج شده از آن است.

تا اینجا فهمیدیم:

• دبی چیست و از چه رابطه‌ای به‌دست می‌آید.
• واحد اندازه‌گیری دبی چیست.
• فرمول محاسبه دبی جریان چیست.
• دبی جرمی چیست.

در ادامه، برای درک مفاهیم فوق، چند مثال ساده را با یکدیگر حل می‌کنیم.

حل مثال های دبی جریان

دبی جریان به صورت مقدار حجم آب یا مایع جابجا شده از مقطعی مشخص در مدت زمان t، تعریف می‌شود. در ادامه، برای درک بهتر این مفهوم چند مثال را با یکدیگر حل می‌کنیم.

مثال اول دبی جریان

نرخ جریان حجمی در لوله‌ای دایره‌ای به قطر ۴ متر، برابر ۵۰ متر مکعب بر ثانیه است. سرعت آب را داخل لوله به‌دست آورید.

پاسخ

قطر لوله برابر ۴ متر و شعاع آن برابر ۲ متر و نرخ جریان حجمی یا $$\frac { \triangle V } { \triangle t }$$ برابر ۵۰ متر مکعب بر ثانیه است.

$$\frac { \triangle V } { \triangle t }=
50 \ \frac { m ^ 3 } { s }$$

حجم برابر حاصل‌ضرب سطح مقطع در ارتفاع است. در این مثال، ارتفاع برابر جابجایی افقی آب در لوله خواهد بود.

$$V = A h =  A d $$

از آنجا که سطح مقطع لوله ثابت است، تغییرات حجم برابر تغییرات جابجایی افقی آب در لوله است.

$$\triangle V = A \triangle d \\ \frac { \triangle V } { \triangle t } = \frac { A \triangle d } { \triangle t }$$

جابجایی بر زمان برابر سرعت است:

$$ \frac { \triangle V } { \triangle t } = A . v$$

با قرار دادن مقدارهای داده شده در سوال، سرعت جریان آب در لوله را به‌دست می‌آوریم:

$$ \frac { \triangle V } { \triangle t } = A . v \\
50 \ \frac{ m ^ 3 } { s } = \pi ( 2 ^ 2 ) v \\
50 = 4 \pi v \\ v = 3.98 \ \frac{ m } { s }$$

مثال دوم دبی جریان

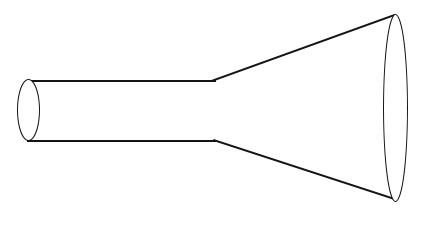
آب درون لوله‌ای با سطح مقطع ۱۰ سانتی‌متر مربع با سرعت ۳ متر بر ثانیه جریان دارد. اگر سطح مقطع لوله به سمت راست به مقدار ۵ سانتی‌متر مربع کاهش یابد، سرعت جریان آب چه تغییری خواهد کرد؟

پاسخ

در این مثال، سطح مقطع لوله ثابت نیست و با حرکت آب به سمت راست، کاهش می‌یابد. سرعت حرکت آب در سمت چپ لوله با سطح مقطع بزرگ‌تر داده شده است، سرعت حرکت آب را در سمت راستِ لوله با سطح مقطع کوچک‌تر می‌خواهیم. قبل از حل این مثال به پاسخ این پرسش فکر کنید. آیا می‌دانید با کاهش سطح مقطع لوله، سرعت جریان آب در لوله چه تغییری می‌کند؟ فرض کنید با استفاده از شلنگ آبی با سطح مقطعی مشخص، باغچه خانه خود را آب می‌دهید. انگشت شصت خود را در دهانه خروجی شلنگ قرار می‌دهید. چه اتفاقی می‌افتد؟ آب با سرعت بیشتری خارج می‌شود. بنابراین، این‌گونه به نظر می‌رسد که با کاهش سطح مقطع لوله، سرعت حرکت آب در آن افزایش می‌یابد.

همان‌طور که در بخش‌ قبل دیدیم، دبی جرم ثابت است. مقدار جرم آب ورودی به لوله در زمان t برابر مقدار جرم آبِ خروجی از لوله در همان زمان است.

$$\frac { \triangle m } { \triangle t } = cte$$

جرم، برابر حاصل‌ضرب چگالی در حجم است،:

$$m = \rho v$$

رابطه فوق را در رابطه $$\frac { \triangle m } { \triangle t } = cte$$ قرار می‌دهیم، در نتیجه حاصل‌ضرب مساحت، چگالی و سرعت در یکدیگر مقداری ثابتی را به ما می‌دهد:

$$\rho A v = ctr$$

نقطه ورودی به لوله را نقطه یک و نقطه خروجی از لوله را نقطه ۲ در نظر می‌گیریم:

$$\rho_1 A_1 v_1 = \rho_2 A_2 v_2 $$

از آنجا که چگالی آب در سراسر لوله ثابت است، با حذف آن از طرفین به معادله پیوستگی به‌دست آمده در بخش‌های قبل، می‌رسیم:

$$\ A_1 v_1 = A_2 v_2 $$

مقدارهای داده شده در مثال را در رابطه فوق قرار می‌دهیم:

$$10 \ cm^ 2 \times 3 \ \frac{ m } { s } =
5 \ cm^ 2 \times v_2 \\ v_ 2 = 6
\ \frac { m } { s }$$

مثال سوم دبی جریان

آب با سرعت ۵ متر بر ثانیه در لوله‌ای با شعاع ۴ سانتی‌متر حرکت می‌کند. الف) اگر شعاع لوله در ادامه مسیر برابر ۸ سانتی‌متر شود، سرعت جریان آب در لوله چه مقدار خواهد شد؟ ب) نرخ جریان حجمی یا دبی جریان داخل لوله چه مقدار است؟ ج) نرخ جریان جرمی یا دبی جرمی را به‌دست آورید.

پاسخ

قسمت الف: برخلاف مثال ۲، شعاع لوله در این مثال افزایش می‌یابد و دو برابر می‌شود. آیا می‌دانید با افزایش شعاع لوله، سرعت حرکت آب چگونه تغییر می‌کند؟ با افزایش شعاع لوله، سطح مقطع آن افزایش خواهد یافت. در نتیجه، آب با سرعت کمتری حرکت خواهد کرد. برای به‌دست آوردن سرعت از معادله پایستگی استفاده می‌کنیم:

$$A_1 v_ 1 = A_2 v_2 \\ \pi r _1^2 v_1 = \pi r^2_2
v_ 2 \\ r_1^2 v_1 = r_2^2v_2 \\ 4 ^ 2 \times 5 =
8 ^ 2 v_2 \\ v_2 = 1.25 \ \frac { m } { s }$$

قسمت ب: در این بخش می‌خواهیم دبی جریان داخل لوله را به‌دست آوریم. همان‌طور که در ابتدای مطلب دیدیم، دبی جریان با استفاده از رابطه $$\frac { \triangle V } { \triangle t }$$ به‌دست می‌آید:

$$\frac { \triangle V } { \triangle t } = A v $$

دبی جریان در سمت چپ لوله برابر است با:

$$\frac { \triangle V } { \triangle t } = A v \\ = \pi r_1 ^ 2 v_1 = \pi (0.04 \ m) ^ 2 (5 \ \frac { m } { s } ) \\ = 0.0251 \ \frac { m ^ 3 } { s } $$

دبی جریان در سراسر لوله یکسان است، بنابراین مقدار آن در انتهای سمت راست لوله نیز باید برابر $$0.0251 \ \frac { m ^ 3 } { s }$$ باشد:

$$\frac { \triangle V } { \triangle t } = A v \\ = \pi r_‌2 ^ 2 v_2 = \pi (0.08 \ m) ^ 2 (1.25 \ \frac { m } { s } ) \\ = 0.0251 \ \frac { m ^ 3 } { s } $$

قسمت ج: در این بخش می‌خواهیم دبی جرمی داخل لوله را به‌دست آوریم. همان‌طور که در ابتدای مطلب دیدیم، دبی جرمی با استفاده از رابطه $$\frac { \triangle m } { \triangle t }$$ به‌دست می‌آید:

$$\frac { \triangle V } { \triangle t } = \rho A v $$

دبی جریان در سمت چپ لوله برابر است با:

$$\frac { \triangle m } { \triangle t } = \rho A v \\ = \rho \pi r_1 ^ 2 v_1 =( 1000 \ \frac { kg } { m ^ 3 }) \pi (0.04 \ m) ^ 2 (5 \ \frac { m } { s } ) \\ = 25.1 \ \frac { kg } { s } $$

شاید از خود پرسیده باشید دبی جریان و دبی جرمی چه رابطه‌ای با یکدیگر دارند. همان‌طور که در قسمت ب دیدیم، دبی جریان با استفاده از رابطه $$\frac { \triangle V } { \triangle t } = A v $$ به‌دست می‌آید. در نتیجه، دبی جرمی را نیز می‌توانیم به صورت زیر بنویسیم:

$$\frac { \triangle m } { \triangle t } = \rho A v \\ \frac { \triangle m } { \triangle t } = \rho \ \frac { \triangle V } { \triangle t }$$

بنابراین، برای به‌دست آوردن دبی جرمی، از رابطه فوق نیز می‌توانیم استفاده کنیم. دبی جریان را در قسمت ب و برابر ۰/۰۲۵۱ متر مکعب بر ثانیه به‌دست آوردیم:

$$\frac { \triangle m } { \triangle t } = \rho \ \frac { \triangle V } { \triangle t } \\ = (1000 \ \frac { kg } { m^ 3 } ) (0.0251 \ \frac { m ^ 3 } { s } ) = 25.1 \ \frac { kg } { s }$$

مثال چهارم دبی جریان

آب با سرعت ۱/۵ متر بر ثانیه داخل لوله‌ای دایره‌ای به شعاع ۱۵ سانتی‌متر جریان دارد و داخل مخزنی ذخیره ریخته می‌شود. الف) دبی جریان چه مقدار است؟ ب) مقدار جرم آب که در ۱۰ دقیقه به سمت مخزن ذخیره حرکت می‌کند را به‌دست آورید. ج) ۲۵۰ هزار کیلوگرم آب در چه مدت زمانی وارد مخزن شود؟

پاسخ

قسمت الف: آب با سرعت ۱/۵ متر بر ثانیه داخل لوله‌ای با شعاع ۱۵ سانتی‌متر به سمت مخزنی برای ذخیره آب، جریان دارد. در قسمت الف می‌خواهیم دبی جرمی را به‌دست آوریم. دبی جرمی برابر مقدار جرم آبِ گذرنده از نقطه‌ای مشخص درون لوله در مدت زمان t است.

$$\frac { \triangle m } { \triangle t } = \rho \ A v = (1000 \ \frac { kg } { m ^ 3 } ) \pi ( 0.15 \ m) ^ 2 (1.5 \ \frac { m } { s }) = 105.98 \ \frac { kg } { s }$$

قسمت ب: در این قسمت می‌خواهیم جرم آبی که در مدت ۱۰ دقیقه داخل مخزن ذخیره می‌ریزد را به‌دست آوریم. آب با سرعت ۱/۵ متر بر ثانیه داخل لوله‌ای دایره‌ای به قطر ۱۵ سانتی‌متر جریان دارد و داخل مخزنی استوانه‌ای ریخته می‌شود. آب درون لوله با سرعت ۱/۵ متر بر ثانیه به سمت مخزن ذخیره حرکت می‌کند.

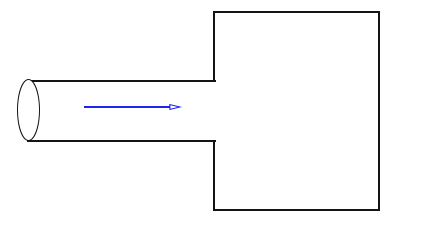
در قسمت الف، دبی جرمی یا نرخ جریان جرمی را برابر ۱۰۵/۹۸ کیلوگرم بر ثانیه به‌دست آوردیم. این عدد چه معنایی دارد؟ در هر ثانیه در حدود ۱۰۶ کیلوگرم آب داخل مخزن می‌ریزد. برای آن‌که بدانیم در ۱۰ دقیقه، چه مقدار آب وارد مخزن می‌شود، باید ۱۰ دقیقه را به ثانیه تبدیل کنیم. هر دقیقه ۶۰ ثانیه و ۱۰ دقیقه برابر ۶۰۰ ثانیه است. در نتیجه، مقدار آب ورودی به مخزن در ۱۰ دقیقه برابر است با:

$$\triangle m = 600 \times 105.98 = 63588 \ kg$$

قسمت ج: در این قسمت می‌خواهیم زمان لازم برای ورود ۲۵۰ هزار کیلوگرم آب به مخزن را به‌دست آوریم. دبی جرمی در قسمت الف را برابر ۱۰۵/۹۸ کیلوگرم بر ثانیه به‌دست آوردیم. این عدد بدان معنا است که در هر ثانیه، ۱۰۵/۹۸ کیلوگرم آب به مخزن وارد می‌شود. برای به‌دست آوردن مدت زمان ورود ۲۷۰ هزار کیلوگرم آب به مخزن، ایتدا این عدد را بر دبی جرمی تقسیم می‌کنیم.

$$\frac { m } { \frac { \triangle m } { \triangle t } }= \frac { 270000\ kg } { 105.98 \ \frac { kg } { s } } = 2547 \ s$$

عدد به‌دست آمده، مدت زمان ورود ۲۷۰ هزار کیلوگرم آب را به داخل مخزن برحسب ثانیه می‌دهد. برای تبدیل این عدد به دقیقه، آن را بر ۶۰ تقسیم می‌کنیم.

$$\frac { 2547 } { 60 } = 42 \ min $$

مثال پنجم دبی جریان

آب با سرعت ۲/۵ متر بر ثانیه داخل لوله‌ای دایره‌ای به قطر ۱۰ سانتی‌متر جریان دارد و داخل استخری مستطیلی ریخته می‌شود. الف)‌ مقدار دبی چیست. ب)‌ پر کردن استخری به طول ۱۵ متر، عرض ۱۲ متر و ارتفاع ۳ متر، چه مقدار طول می‌کشد؟

پاسخ

قسمت الف: در این قسمت می‌خواهیم دبی جریان داخل لوله را به‌دست آوریم. همان‌طور که در ابتدای مطلب دیدیم، دبی جریان با استفاده از رابطه $$\frac { \triangle V } { \triangle t }$$ به‌دست می‌آید:

$$\frac { \triangle V } { \triangle t } = A v $$

دبی جریان در سمت چپ لوله برابر است با:

$$\frac { \triangle V } { \triangle t } = A v \\ = \pi r_1 ^ 2 v = \pi (0.05 \ m) ^ 2 (2.5 \ \frac { m } { s } ) \\ = 0.0196 \ \frac { m ^ 3 } { s } $$

قسمت ب: آب داخل لوله، داخل استخری به طول ۱۵ متر، عرض ۱۲ متر و ارتفاع ۳ متر می‌ریزد. برای آن‌که بدانیم استخر در چه بازه زمانی به طور کامل پر می‌شود، ابتدا حجم آن را به‌دست می‌آوریم.

$$V = l w h = 15 \times 12 \times 3 = 540 \ m^ 3$$

حجم و دبی جریان را داریم، بنابراین به راحتی می‌توانیم زمان لازم برای پر شدن استخر را به‌دست آوریم. در هر ثانیه، حجمی برابر ۰/۰۱۹۶ متر مکعب از استخر پر می‌شود، حجم ۵۴۰ متر مکعب در چه زمانی پر خواهد شد؟ ۵۴۰ را بر ۰/۰۱۹۶ تقسیم می‌کنیم.

$$\frac { 540 } { 0.0196 } = 24551 \ s \\ \frac { 27551 } { 60 } = 459 \ min$$

مثال ششم دبی جریان

مثال هفتم دبی جریان

جمع‌بندی

در این مطلب از مجله فرادرس، ابتدا به پرسش دبی چیست به زبان ساده پاسخ دادیم. به مقدار حجم آب یا مایع جابجا شده از مقطعی مشخص در مدت زمان t، دبی جریان گفته می‌شود. واحد اندازه‌گیری دبی در سیستم SI، متر مکعب بر ثانیه یا $$\frac { m ^ 3 } { s}$$ است. همچنین، مفهوم دیگری به نام دبی جرمی نیز وجود دارد. به مقدار جرم سیالِ عبوری از نقطه‌ای مشخص در واحد زمان، دبی جرمی یا نرخ جرمی جریان گفته می‌شود. در ادامه مطلب و برای درک بهتر این دو مفهوم، مثال‌هایی را با یکدیگر حل کردیم.