دبی جریان — به زبان ساده

در مطالب گذشته وبلاگ فرادرس در مورد موتور جت و موتور‌های احتراق داخلی صحبت شد. یکی از پارامتر‌های مهم به‌ منظور کارکرد بهینه بسیاری از سیستم‌های احتراقی، تنظیم دبی جریان و سوخت در آن‌ها است. اما شاید این سوال را در ذهن داشته باشید که دبی جریان چیست و چگونه محاسبه می‌شود؟ از این رو در این مطلب قصد داریم تا مفهوم دبی جریان را معرفی کرده و مثال‌هایی نیز از آن ارائه دهیم.

مشخصه‌های جریان

معمولا از بردار‌های سرعت به‌ منظور تحلیل انواع مختلف جریان‌ها در مکانیک سیالات استفاده می‌شود.

فیلم آموزش مکانیک سیالات 1 – جامع و با نکات کاربردی در فرادرس

کلیک کنید

برای نمونه نحوه توزیع جریان باد را می‌توان با استفاده از نشان دادن بردار‌های سرعت در هر نقطه نشان داد. شکل زیر بردار‌های سرعت مربوط به طوفان سال ۲۰۱۴ را نشان می‌دهد.

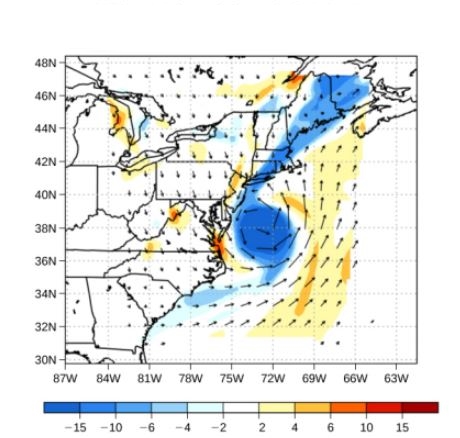
روش دیگر به‌منظور نشان دادن نحوه حرکت سیال، استفاده از خطوط جریان است. خط جریان، نشان‌دهنده مسیر یک جزء‌ از سیال است که مسیر مشخصی را طی کرده است. توجه داشته باشید که همواره بردار سرعت سیال به خط جریان مماس است. در نتیجه با داشتن کانتور بردار‌های سرعت می‌توان شکل خط جریان را نیز حدس زد. در شکل زیر بردار‌های سرعت مربوط به دو نوع جریان مختلف نشان داده شده است.

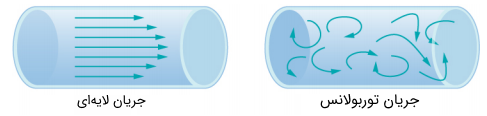
شکل سمت چپ، جریانی لایه‌ای را نشان می‌دهد که در آن لایه‌های سیال به‌صورت موازی با هم حرکت کرده و در یکدیگر مخلوط نمی‌شوند. این در حالی است که در شکل سمت راست لایه‌های جریان مومنتوم بیشتری دارند؛ در نتیجه لایه‌های سیال با هم مخلوط شده و جریان به‌صورت توربولانس در می‌آید.

دبی جریان و رابطه آن با سرعت

به حجم جریان عبوری از یک مجرا، در بازه‌ای مشخص، نرخ جریان یا دبی جریان گفته می‌شود که آن را با $$Q$$ نشان می‌دهند. با توجه به این تعریف، مقدار لحظه‌ای دبی جریان برابر است با:

$$\large q = \frac { d V } { d t }$$

فیلم آموزش مقدماتی مدل سازی بارش و رواناب با نرم افزار HEC-HMS در فرادرس

کلیک کنید

در رابطه فوق $$V$$ نشان‌دهنده حجم بوده و $$t$$ مدت زمان را نشان می‌دهد. با توجه به شکل زیر، حجم بخشی از استوانه به طول $$x$$، برابر با $$A x$$ است.

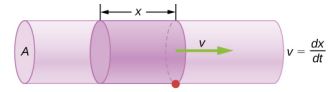
در نتیجه مقدار دبی جریان نیز برابر می‌شود با:

$$Q = \frac { d V } { d t } = \frac { d } { d t } ( A x ) = A \frac { d x }{ d t } = A v$$

نکته مهم در روابط این است که $$v$$ نشان‌دهنده سرعت و $$V$$ نشان‌دهنده حجم است. واحد $$SI$$ دبی جریان، $$m ^ 3 /s$$ در نظر گرفته شده است. با این حال واحد‌های دیگری همچون لیتر بر دقیقه یا گالن بر ثانیه نیز برای بیان کردن این کمیت استفاده می‌شود. توجه داشته باشید که هر لیتر برابر با $$\frac {1}{1000}$$ مترمکعب یا $$10 ^ { 3 }$$ سانتی‌متر مکعب است. نهایتا می‌توان فرمول ساده شده محاسبه دبی جریان را به‌صورت زیر بیان کرد:

$$Q = A v$$

در رابطه فوق فرض بر این است که مساحتِ $$A$$ و سرعتِ $$v$$ ثابت بوده و با گذشت زمان تغییر نمی‌کنند. این رابطه بیان می‌کند که با ثابت بودن هریک از کمیت‌های فوق و افزایش کمیت بعدی، اندازه دبی نیز زیاد خواهد شد. در مواردی که با سیالی تراکم‌ناپذیر روبرو هستیم، مقدار مجموع ورودی‌های یک مجرا برابر با مجموع دبی در خروجی‌های آن است. به‌منظور درک بهتر لوله زیر را در نظر بگیرید. فرض کنید آبی با دبی معلومی به این لوله وارد می‌شود ($$Q _ 1$$). با توجه به تراکم‌ناپذیر بودن سیال، می‌توان گفت که مقدار دبی ورودی و خروجی با هم برابر است. از این رو برای این مجرا می‌توان رابطه زیر را بیان کرد:

$$\begin {split} \color {white} { Q _ { 1 } , = Q _ { 2 }, , A _ { 1 } v _ { 1 } , = A _ { 2 } } Q _ { 1 } & = Q _ { 2 }, \\ A _ { 1 } v _ { 1 } & = A _ { 2 } v _ { 2 } \ldotp \color {white} { Q _ { 1 } , = Q _ { 2 }, , A _ { 1 } v _ { 1 } , = A _ { 2 } } \end {split}$$

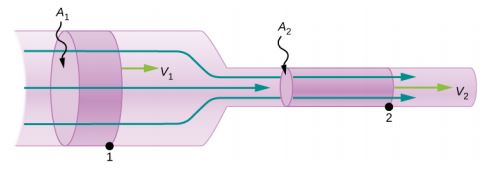
به معادله فوق، معادله پیوستگی نیز گفته می‌شود. البته شکل این معادله برای سیالات قابل تراکم متفاوت است. حس فیزیکی معادله پیوستگی را می‌توانید در جریان یافتن آب درون لوله ببینید. همان‌طور که احتمالا تجربه کرده‌اید اگر لوله یا مجرای آب را فشار دهید، سطح مقطع کم شده و سرعت سیال نیز افزایش می‌یابد. شکل فوق نیز چنین مفهومی را نشان می‌دهد. البته در ادامه مثالی ارائه شده که می‌توانید با مطالعه آن، با جزئیات کمی معادله پیوستگی بیشتر آشنا شوید.

مثال

لوله‌ای را در نظر بگیرید که قطر آن برابر با $$0.5 c m$$ است. فرض کنید لوله را به مجرایی به شعاع $$0.9 c m$$ متصل کنیم. هم‌چنین دبی جریان آب را برابر با $$0.500 L / s$$ در نظر بگیرید. سرعت آب را در لوله و در مجرا بدست آورید.

در حالت کلی زمانی که دبی جریان سیالی در مجرایی به سطح $$A$$ یا شعاع $$r$$ برابر با $$Q$$ باشد، سرعتِ $$v$$ مطابق با رابطه زیر بدست می‌آید.

$$\color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } } v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } \color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } }$$

در این مسئله نیز کافی است تا رابطه فوق را برای لوله و مجرا استفاده کرده و سرعت را در آن‌ها بدست آورد. توجه داشته باشید که دبیِ جریان در هر دو مسیر، با هم برابر است. سرعت در مجرای بزرگ‌تر، برابر است با:

$$\color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } } v = \frac { ( 0.500 \; L / s ) ( 1 0 ^ { - 3 } \; m ^ { 3 } /L ) }{ (3.14) ( 9.00 \times 10 ^ { - 3 } \; m ) ^ { 2 } } = 1.96 \; m / s \color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } }$$

حال می‌خواهیم سرعت را در لوله بدست آوریم. بدین منظور می‌توان از دو روش استفاده کرد. روش اول به این صورت است که، به‌طور مستقیم از رابطه ارائه شده در بالا استفاده کنیم و روش دوم استفاده از مفهوم ثابت بودن دبی است. با توجه به تراکم‌ناپذیر بودن جریان، می‌توان رابطه زیر را بین سرعت‌ها و مساحت‌‌ها بیان کرد:

$$\color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } } A _ { 1 } v _ { 1 } = A _ { 2 } v _ { 2 } \color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } }$$

اندیس‌های $$1$$ نشان‌دهنده لوله و اندیس $$2$$ نشان‌دهنده مجرای بزرگ‌تر است. با استفاده از تساوی بالا، $$v _ 2$$ مطابق با رابطه زیر قابل محاسبه است.

$$\color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } } v_{2} = \frac { A _ { 1 } } { A _ { 2 } } v_{1} = \frac{\pi r_ { 1}^ { 2 } } {\pi r _ { 2 } ^ { 2 } } v _ { 1 } = \frac { r _ { 1 } ^{ 2 } }{r_ { 2 } ^ { 2 } } v _ { 1 } \color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } }$$

با قرار دادن مقادیر عددی در رابطه فوق، سرعتِ $$v _ 2$$ برابر می‌شود با:

$$\color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } } v_{2} = \frac { (0.900\; cm ) ^ { 2 } } { ( 0.250\; cm) ^ { 2 } } (1.96\; m / s ) = 25.5\; m / s \color {white} { v = \frac { Q } { A } = \frac { Q } { \pi r _ { 1 } ^ { 2 } } }$$

پایستگی جرم

سرعت جریان سیال را می‌توان با استفاده از نرخ جرمی جریان یا جریان جرمی نیز مشخص کرد.

فیلم آموزش انتقال جرم – مرور و حل تست کنکور ارشد و دکتری در فرادرس

کلیک کنید

این مقدار برابر با مقدار جرمی از سیال است که در واحد زمان از نقطه‌ای مشخص عبور می‌کند. به منظور بدست آوردن رابطه جریان جرمی بار دیگر، مجرایی همچون شکل زیر را در نظر بگیرید.

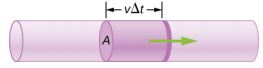
همان‌طور که می‌دانید مقدار جرم اشغال شده در حجم $$V$$ برابر است با:

$$m = \rho V = \rho A x$$

در رابطه فوق $$\rho$$ نشان‌دهنده چگالی است. در این صورت مشتق زمانی جرم، نشان‌دهنده دبی جرمی جریان است که مطابق با رابطه زیر بدست می‌آید.

$$\frac { d m } { d t } = \frac { d }‌ { d t } ( \rho A x ) = \rho A \frac { d x } { d t } = \rho A v$$

دبی جرمی جریان، یک کمیت مهم در دینامیک سیالات محسوب می‌شود و در حل بسیاری از مسائل مکانیک سیالات از آن استفاده می‌شود. توجه داشته باشید که نسبت استفاده شده در مثال را می‌توان برای دبی جرمی جریان نیز بیان کرد. در حقیقت با فرض تراکم‌ناپذیر بودن سیال در یک مجرا، رابطه زیر را می‌توان نوشت:

$$A _ { 1 } v _ { 1 } = A _ { 2 } v _ { 2 }$$

با توجه به تراکم‌ناپذیر بودن جریان می‌توان گفت چگالی‌ها با هم برابر هستند. در نتیجه معادله فوق نهایتا به‌شکل زیر در می‌آید.

$$\color {white} {A _ { 1 } v _ { 1 } = A _ { 2 } v _ { 2 } } A _ { 1 } v _ { 1 } = A _ { 2 } v _ { 2 } \color {white} { A _ { 1 } v _ { 1 } = A _ { 2 } v _ { 2 } }$$

همان‌طور که می‌بینید با نوشتن پایستگی دبی جرمی جریان نیز می‌توان به نتیجه‌ای مشابه با دبی حجمی دست یافت.

در صورتی که مطلب بالا برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• استاتیک سیالات — به زبان ساده
• سینماتیک سیالات — مقدمه‌ای بر مکانیک
• دینامیک سیالات محاسباتی (CFD) — از صفر تا صد

^^