حل دالامبر معادله موج — به زبان ساده

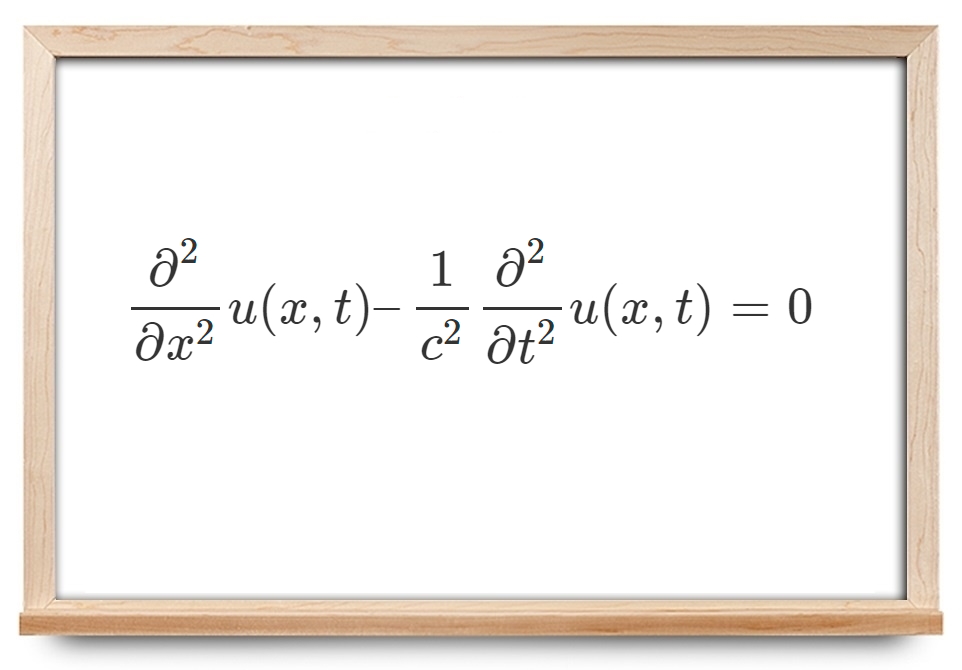
در آموزش‌های پیشین مجله فرادرس، با معادله موج آشنا شدیم. یکی از روش‌های حل معادله موج، حل دالامبر است که در این آموزش آن را شرح خواهیم داد.

معادله موج

معمولاً مطالعه راه‌حل کلی و جواب عمومی معادله دیفرانسیل با مشتقات جزئی مفید نیست. از آنجا که موارد استثنایی وجود دارد، هر گزاره عمومی در مورد آن‌ها باید واجد شرایط لازم باشد. یکی از این‌ها معادله موج یک‌بعدی است:

فیلم آموزش ریاضی مهندسی در فرادرس

کلیک کنید

$$ \large \dfrac { \partial ^ 2  } {  \partial x ^ 2  }  u  ( x , t ) - \frac { 1 } {  c ^ 2 }  \dfrac { \partial ^ 2  } { \partial t ^  2 } u ( x ,  t ) = 0 , $$

که یک جواب عمومی دارد و آن را ریاضیدان فرانسوی، «دالامبر» (d’Alembert) ارائه کرد که به حل دالامبر مشهور است.

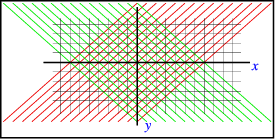
این راه‌حل هنگامی آشکار می‌شود که فیزیک مسئله را در نظر بگیریم: معادله موج امواجی را توصیف می‌کند که با سرعت $$c$$ (سرعت صوت، نور یا هر چیز دیگری) منتشر می‌شوند. بنابراین هرگونه اغتشاش در محیط یک‌بعدی با چنین سرعتی به سمت راست یا چپ گسترش می‌یابد. این بدین معنی است که انتظار داریم جواب‌ها در امتداد مشخصه‌های $$x\pm ct=\text{constant}$$ (همان‌طور که در شکل ۱ دیده می‌شود) انتشار یابند.

حل دالامبر معادله موج

برای درک تمام جزئیات ریاضی راه‌حل، متغیرها را تغییر می‌دهیم:

$$ \large w = x + c t , \quad z = x - c t . $$

می‌نویسیم $$ u ( x  , t ) = \bar u ( w ,  z ) $$ و خواهیم داشت:

$$ \large \begin {align} \dfrac { \partial } { \partial x }  u &  = \dfrac { \partial } { \partial w } { \bar u } \dfrac { \partial }{ \partial x }  w + \dfrac { \partial } { \partial z } { \bar u } \dfrac { \partial } { \partial x }   z = \dfrac { \partial } { \partial w }{ \bar u }  + \dfrac { \partial } { \partial z } { \bar u } , \nonumber \\[4pt] \dfrac { \partial ^ 2 }  { \partial x ^ 2 }  u & = \dfrac { \partial ^ 2 }  { \partial w ^ 2  } {  \bar u } + 2   \dfrac { \partial ^  2 }  { \partial w \partial z } { \bar u } +  \dfrac { \partial ^ 2} { \partial z ^ 2 } { \bar u } , \nonumber\\[4pt] \dfrac { \partial }  { \partial t } u & = \dfrac { \partial } { \partial w } { \bar u } \dfrac { \partial }  { \partial t } w + \dfrac { \partial } { \partial z } { \bar u } \dfrac { \partial } { \partial t }  z = c \left ( \dfrac { \partial } { \partial w } { \bar u } -  \dfrac { \partial } { \partial z }  { \bar u } \right ) ,  \nonumber\\[4pt] \dfrac { \partial ^ 2 }  { \partial t ^ 2 }  u & = c ^  2 \left ( \dfrac { \partial ^ 2 } { \partial w ^ 2 }  { \bar u } - 2  \dfrac { \partial ^ 2 }  { \partial w \partial z } { \bar u } + \dfrac { \partial ^ 2} { \partial z ^ 2 } { \bar u } \right ) \end {align} $$

نتیجه می‌گیریم:

$$ \large \dfrac { \partial ^ 2 }  { \partial x ^ 2 }  u  ( x , t )  - \frac { 1 } { c ^ 2 }   \dfrac { \partial ^ 2  } { \partial t ^ 2  }  u ( x , t )  = 4 \dfrac { \partial ^ 2 }  { \partial w \partial z }   { \bar u }  = 0 $$

معادله‌ای به فرم $$ \dfrac { \partial ^ 2 } { \partial w \partial z } { \bar u } = 0 $$ را می‌توان به سادگی با انتگرالگیری نسبت به $$z$$ و $$w$$ حل کرد. ابتدا برای وابسته به $$z$$ داریم:

$$ \large \dfrac { \partial } { \partial w } { \bar u } = \Phi ( w ) $$

که $$\Phi$$ هر تابعی فقط از $$w$$ است. اکنون معادله را با استقلال نسبت به $$w$$ حل می‌کنیم:

$$ \large \bar u ( w , z ) = \int \Phi ( w ) d w = F ( w ) + G ( z ) $$

به عبارت دیگر، $$F$$ و $$G$$ توابعی دلخواه هستند.

حل دالامبر معادله تار نامحدود

معادله زیر در کاربردهای عملی کاملاً مفید است. ابتدا به چگونگی استفاده از این مسئله، وقتی که تار بی‌نهایت داریم، نگاه می‌کنیم (محدودیتی در $$x$$ وجود ندارد). فرض کنید که در حال بررسی مسئله‌ای با شرایط اولیه زیر هستیم:

$$ \large u ( x , 0 ) = f ( x ) , \; \; \dfrac { \partial } { \partial t } u ( x , 0 ) = g ( x ) . $$

فیلم آموزش ریاضیات مهندسی پیشرفته در فرادرس

کلیک کنید

فرض می‌کنیم $$f(\pm\infty)=0$$. همچنین، فرض می‌کنیم که این برای $$F$$ و $$G$$ نیز صدق می‌کند (مجبور به این فرض نیستیم، اما این کار برخی از ثابت‌های دلخواه را که در $$u$$ نقش بازی نمی‌کنند حذف می‌کند). داریم:

$$ \large \begin {align} F ( x ) + G ( x ) & = f ( x ) , \nonumber\\[4pt] c ( F' ( x ) - G' ( x ) ) & = g ( x ) . \end {align} $$

معادله آخر را می‌توان به صورت زیر نوشت:

$$ \large F ( x ) - G ( x ) = \underbrace { \frac { 1 } { c } \int _ 0 ^ x g ( y ) d y } _ { = \Gamma ( x ) } + C $$

دقت کنید که $$\Gamma$$ انتگرال $$g$$ است. بنابراین، $$\Gamma$$ همواره یک تابع پیوسته خواهد بود، حتی اگر $$g$$ پیوسته نباشد.

در نهایت، می‌توان نوشت:

$$ \large \begin {align} F ( x ) & = \dfrac { 1 } { 2 } \left [ f ( x ) + \Gamma ( x ) + C \right ] \nonumber\\[4pt] G ( x ) & = \dfrac { 1 } { 2 } \left [ f ( x ) - \Gamma ( x ) - C \right ] \end {align} $$

فرض کنید، داریم (برای سادگی $$c=1 \text{m/s} $$ را انتخاب می‌کنیم):

$$ \large f ( x ) = \begin {cases} x + 1 & \text {if $-1<x<0$} \\ 1 - x & \text {if $0<x<1$} \\ 0 & \text {elsewhere} \end {cases} . $$

و $$ g ( x ) = 0 $$. جواب به سادگی به صورت زیر است:

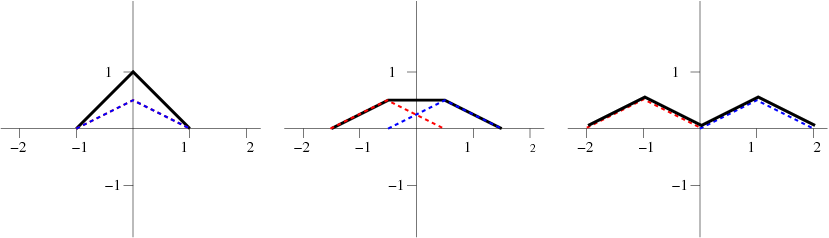
$$ \large u ( x , t ) = \dfrac { 1 } { 2 } \left [ f ( x + t ) + f ( x - t ) \right ] . $$

این را می‌توان به راحتی به صورت گرافیکی حل کرد.

حل دالامبر معادله تار محدود

حل دالامبر معادله تار متناهی پیچیده‌تر است. در اینجا با این مشکل روبرو می‌شویم که حتی اگر $$f$$ و $$g$$ فقط برای $$0<x<a$$ معلوم باشند، $$x\pm ct$$ می‌تواند هر مقداری را از $$-\infty$$ به $$\infty$$ داشته باشد. باید راهی برای ادامه تابع بیش از طول رشته مشخص کنیم. روش انجام این کار به نوع شرایط مرزی بستگی دارد. در اینجا ما فقط یک رشته ثابت در انتهای آن را در نظر می‌گیریم:

$$ \large \begin {align} u ( 0 , t ) & = u ( a , t ) = 0 , \nonumber\\[4pt] u ( x , 0 ) & = f ( x ) \\[4pt] \dfrac { \partial }{ \partial t } u ( x , 0 ) & = g ( x ) . \end {align} $$

در ابتدا می‌توانیم رویکرد را برای سیستم بی‌نهایت که در بالا ترسیم شده دنبال کنیم و خواهیم داشت:

$$ \large \begin {align} F ( x ) & = \dfrac { 1 } { 2 } \left [ f ( x ) + \Gamma ( x ) + C \right ] , \nonumber\\[4pt] G (x ) & = \dfrac { 1 } { 2 } \left [ f ( x ) - \Gamma ( x ) - C \right ] . \end {align} $$

با توجه به شرایط اولیه $$u(0,t)=0$$، داریم:

$$ \large \dfrac { 1 } { 2 } [ f ( c t ) + f ( - c t ) ] + \dfrac { 1 } { 2 } [ \Gamma ( c t ) - \Gamma ( - c t ) ] = 0 . $$

اکنون فهمیدیم که $$f$$ و $$\Gamma$$ توابع کاملاً دلخواهی هستند و می‌توانیم هر شکلی را برای شرایط اولیه مورد نظر خود انتخاب کنیم. بنابراین رابطه یافت شده در بالا فقط در صورت صفر بودن هر دو عبارت برقرار است:

$$ \large \begin {align} f ( x ) & = - f ( - x ) , \nonumber\\[4pt] \Gamma ( x ) & = \Gamma ( x ) . \end {align} $$

اکنون شرایط مرزی دیگر را اعمال می‌کنیم و داریم:

$$ \large \begin {align} f ( a + x ) & = - f ( a - x ) , \nonumber\\[4pt] \Gamma ( a + x ) & = \Gamma ( a - x ) . \end {align} $$

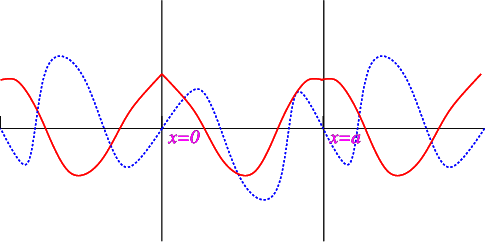
شرایط انعکاس $$f$$ و $$\Gamma$$ مانند سینوس‌ها و کسینوس‌ها است و همان‌طور که از شکل ۳ می‌بینیم $$f$$ و $$\Gamma$$ دارای دوره تناوب $$2a$$ هستند.

معرفی فیلم آموزش ریاضی مهندسی

برای آشنایی بیشتر با حل دالامبر معادله موج و سایر مباحث ریاضیات مهندسی، پیشنهاد می‌کنیم به فیلم آموزش ریاضی مهندسی مراجعه کنید که در قالب ۴ درس و در مدت زمان ۱۵ ساعت و ۵۱ دقیقه تدوین شده است.

موضوع درس اول این آموزش ویدیویی، آنالیز فوریه است که مباحث آن به طور کامل پوشش داده شده است. درس دوم درباره معادلات دیفرانسیل با مشتقات جزئی است. توابع مختلط و نگاشت به طور مفصل در درس سوم مورد بحث قرار گرفته‌اند. در نهایت، موضوع درس چهارم انتگرال‌گیری از توابع مختلط است.

• برای مشاهده فیلم آموزش ریاضی مهندسی + اینجا کلیک کنید.

معرفی فیلم آموزش ریاضی مهندسی (مرور و حل مساله)

یکی دیگر از آموزش‌های فردارس درباره حل دالامبر و ریاضیات مهندسی، آموزش ریاضی مهندسی (مرور و حل مساله) است که در ۱۱ ساعت و ۴۹ دقیقه و د قالب ۱۳ درس تدوین شده است.

درس‌های اول تا سوم این آموزش به مبحث آنالیز فوریه اختصاص داده شده است. معادلات دیفرانسیل با مشتقات جزئی موضوع درس‌های چهارم تا هفتم است. در درس‌های هشتم تا دهم نیز به توابع مختلط و نگاشت پرداخته شده است. در نهایت، درس‌های یازدهم تا سیزدهم موضوع انتگرال‌گیری از توابع مختلط را پوشش می‌دهند.

• برای مشاهده فیلم آموزش ریاضی مهندسی (مرور و حل مساله) + اینجا کلیک کنید.