جبر بولی مجموعه ها — به زبان ساده
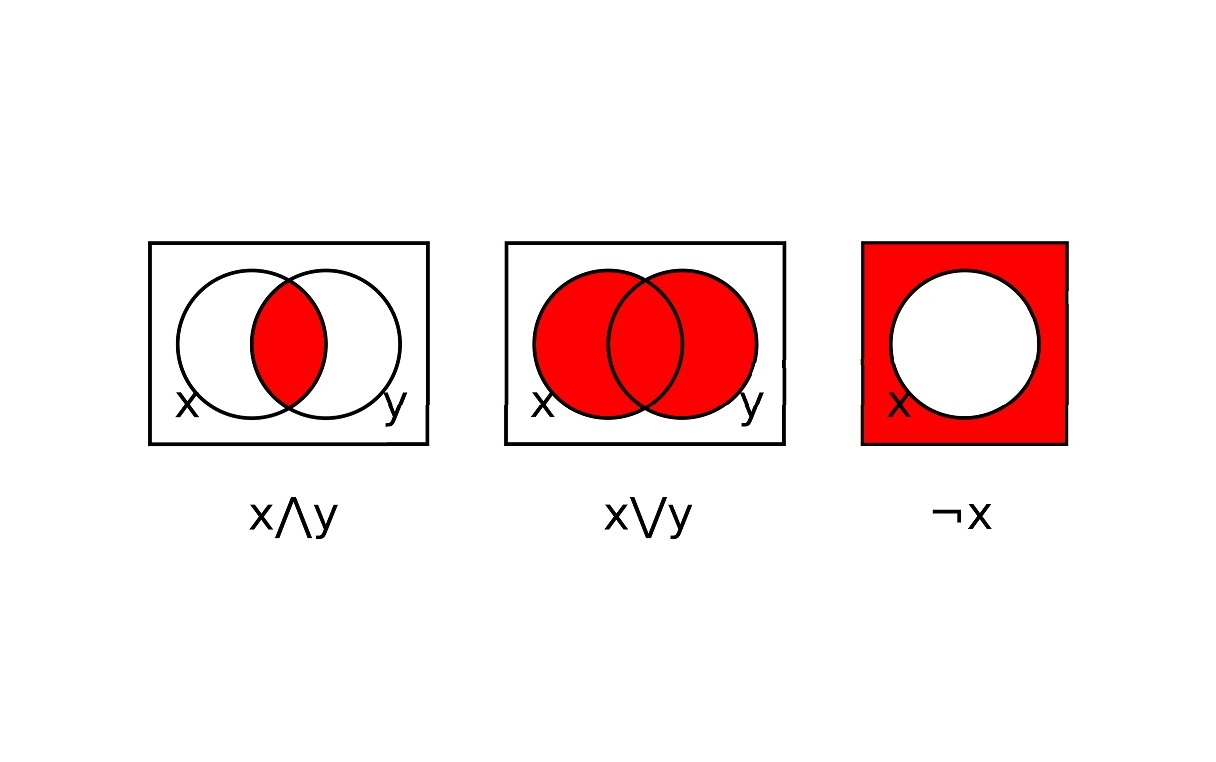
نظریه مجموعهها ارتباط نزدیکی با منطق دارد. اشتراک و اجتماع مجموعهها را میتوان با عملگرهای مبتنی بر «و» منطقی و «یا»ی منطقی بیان کرد. در این آموزش، با ارتباط مجموعهها و منطق و جبر بولی مجموعه ها آشنا میشویم.
جبر بولی در منطق و مجموعه ها
نمادگذاری $$\{x|P(x)\} $$ استفاده از گزارهها را برای مشخص کردن مجموعهها امکانپذیر میکند. اگر $$ A $$ یک مجموعه باشد، آنگاه $$ x \in A $$ یک گزاره را تعریف میکند که برای هر شیء $$ x $$ صحیح است اگر و تنها اگر $$ x $$ عضوی از مجموعه $$ A $$ باشد. بنابراین، نباید تعجب کرد که بسیاری از قواعد و قوانین منطق مشابههایی در نظریه مجموعهها داشته باشند. این همان چیزی است که در جبر بولی مجموعهها وجود دارد.
برای مثال، از قبل میدانیم که $$\cup $$ و $$\cap $$ عملهایی جابهجاییپذیر هستند. این واقعیت را میتوان با استفاده از قوانین منطق تأیید کرد. مجموعههای $$ A $$ و $$ B $$ را در نظر بگیرید. بر اساس تعریف برابری مجموعهها، میتوانیم نشان دهیم که با توجه به $$ ∀x((x∈A∪B)↔(x∈B∪A)) $$ رابطه $$ A \cup B=B \cup A $$ برقرار است. از طرفی، برای هر $$ x $$ داریم:
$$ \large \begin {align*} x \in A \cup B & ↔ x \in A \lor x \in B \\[4pt] & ↔ x \in B \lor x \in A \\[4pt] & ↔ x \in B \cup A \end {align*} $$
جابهجاییپذیری $$ \cap $$ به همان ترتیب از تعریف $$\wedge $$ پیروی میکند که $$\cup $$ از تعریف $$ \lor $$ و استدلال مشابهی را برای شرکتپذیری اجتماع و اشتراک میتوان بیان کرد.
قوانین توزیعپذیری در منطق گزارهای دو قانون مشابه را در نظریه مجموعهها نتیجه میدهند. فرض کنید $$ A $$، $$ B $$ و $$ C $$ سه مجموعه باشند. آنگاه، داریم:
$$ \large A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C) $$
و
$$ \large A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C) $$
این قواعد را قوانین توزیعپذیری نظریه مجموعهها مینامند. برای تأیید اولی، برای هر $$ x $$ میتوان نوشت:
$$ \large \begin {align*} x ∈ A ∪ (B ∩ C) &↔ (x ∈ A) ∨ ((x ∈ B) ∧ (x ∈ C)) \\[4pt]& ↔((x∈A)∨(x∈B))∧((x∈A)∨(x∈C)) \\[4pt]&↔ (x ∈ A ∪ B) ∧ (x ∈ A ∪ C) \\[4pt]&↔ x ∈ ((A ∪ B) ∩ (A ∪ C)) \end{align*} $$
قانون دوم نیز دقیقاً مشابه قانون اول بیان میشود.
با اینکه $$ \cup $$ مشابه $$ ∨ $$ و $$ \cap $$ مشابه $$ ∧ $$ است، هنوز نمیدانیم چه عملگری در نظریه مجموعهها مشابه عملگر نقیض منطقی، یعنی $$ \neg $$ است. برای مجموعه $$ A $$، عبارت $$ {x | ¬(x ∈ A)} $$ را به عنوان مجموعهای که شامل هر چیزی جز آنچه متعلق به $$ A $$ است، تعریف میکنیم.
مجموعه جهانی
متأسفانه قواعد نظریه مجموعهها به ما امکان نمیدهد که چنین مجموعهای را تعریف کنیم. نماد $$ {x | P (x)} $$ را میتوان تنها در حالتی مورد استفاده قرار داد که حوزه گفتمان $$ P$$ یک مجموعه باشد. بنابراین، باید یک مجموعه زیربنایی وجود داشته باشد که عناصر موجود در آن، در $$ A $$ باشند/نباشند، یعنی مجموعه زیربنایی که $$ A $$ یک زیرمجموعه از آن باشد. میتوانیم با محدود کردن بحث به زیرمجموعههای برخی مجموعههای ثابت، این مسئله را حل کنیم. این مجموعه به عنوان «مجموعه جهانی» (Universal Set) شناخته میشود.
توجه کنید که مجموعه جهانی تنها برای مباحث مشخصی جهانی است. در واقع، این مجموعه به اندازه کافی بزرگ است که تمام مجموعههای مورد بحث به عنوان زیرمجموعه آن باشند. با در نظر گرفتن مجموعه جهانی $$ U $$ و هر زیرمجموعه $$ A $$ از $$ U $$، میتوانیم مجموعه $$ \{x ∈ U | ¬(x ∈ A)\} $$ را تعریف کنیم.
مکمل مجموعه
فرض کنید $$ U $$ مجموعه جهانی و $$ A $$ یک زیرمجموعه از آن باشد. مکمل $$ A $$ در $$ U $$ را به صورت $$ \complement{A} = \{x ∈ U | x \notin A\} $$ تعریف میکنیم.
معمولاً، مکمل $$ A $$ در $$ U $$ را برای سادگی همان مکمل $$ A $$ مینامیم، اما باید به یاد داشته باشیم که هر جا از واژه مکمل استفاده شده، مجموعه جهانی را نیز در پس خود دارد و با توجه به آن به دست آمده است.
با توجه به عملیات مکمل روی مجموعهها، میتوانیم قواعد مشابه منطقی را نیز بیابیم. برای مثال، میدانیم $$ p ∧ ¬p = \mathbb{F} $$ برای هر گزاره $$ p $$ برقرار است. برای هر زیرمجموعه $$ A $$ از $$U$$، داریم:
$$ \large \begin {align*} A \cap \complement { A } & = \{ x \in U | ( x \in A ) \land ( x \in \complement ( A ) \} \\[4pt] & = \{ x \in U | ( \in A ) \land ( x \notin A ) \} \\[4pt] & = \{ x \in U | (x \in A ) \land \neg ( x \in A ) \} \ \\[4pt] & = \emptyset \end {align*} $$
تساوی آخر به این دلیل است که گزاره $$ (x ∈ A) ∧ ¬(x ∈ A) $$ برای هر $$ x $$ غلط است. به طور مشابه، میتوانیم نشان دهیم که $$ A∪ \bar{A} = U $$ و $$ \bar{\bar{A}} =A $$ ($$ \bar{\bar{A}} $$ مکمل مکمل $$ A $$ است).
قوانین دمورگان و جبر بولی مجموعهها
مهمترین قوانین برای کار با عناصر مجوعهها، قوانین دمورگان هستند. این قوانین، که مستقیماً از قوانین دمورگان در منطق به دست میآیند، برای هر زیرمجموعه $$ A $$ و $$ B $$ از مجموعه جهانی $$ U $$ تساویهای زیر را بیان میکنند:
$$ \large \bar{A∪B} = \bar{A} \cap \bar{B} $$
و
$$ \large \bar{A∩B} = \bar{A} \cup \bar{B} $$
قوانین جبر بولی مجموعهها
جدول زیر، برخی قوانین جبر بولی را برای مجموعههای $$A$$، $$ B $$ و $$ C $$ نشان میدهد. برای قوانینی که شامل عملگر مکمل است، فرض شده که مجموعهها زیرمجموعه مجموعه جهانی $$U$$ هستند. در بیشتر موارد، این قوانین مستقیماً با منطق گزارهای مطابقت دارند.
| قوانین مکمل دوگانه | $$ \overline {\overline {A}} = A $$ |
| سایر قوانین | $$ \begin {align*} A \cup \overline { A } & = U \\ A \cap \overline { A } & = \emptyset \\ \emptyset \cup A & = A \\ \emptyset \cap A & = \emptyset \end {align*} $$ |
| قوانین خودتوانی | $$ \begin {align*} A \cap A & = A \\ A \cup A & = A \end {align*} $$ |
| قوانین جابهجایی پذیری | $$ \begin {align*} A \cap B & = B \cap A \\ A \cup B & = A \cup B \end {align*} $$ |
| قوانین شرکتپذیری | $$ \begin {align*} A \cap ( B \cap C ) & = ( A\cap B) \cap C \\ A \cup ( B \cup C ) & = ( A\cup B) \cup C \end {align*} $$ |
| قوانین توزیعی | $$ \begin {align*} A \cap ( B \cup C ) & = ( A\cap B) \cup ( A \cap C ) \\ A \cup ( B \cap C ) & = ( A\cup B) \cap ( A \cup C ) \end {align*} $$ |
| قوانین دمورگان | $$ \begin {align*} \overline { A \cap B } & = \overline { A } \cup \overline { B} \\ \overline { A \cup B } & = \overline { A } \cap \overline { B} \end {align*} $$ |
برای مثال، میتوانیم یکی از قوانین دمورگان را با محاسبات زیر تأیید کنیم:
$$ \large \begin {align*} \overline { A \cup B } & = \{ x \in U | x \notin ( A \cup B ) \} \\[4pt] & = \{ x \in U | \neg ( x \in A \cup B)\} \\[4pt] &= \{ x \in U | \neg ( x \in A \lor x \in B )\} \\[4pt] &= \{ x \in U | (\neg ( x \in A ) ) \land ( \neg ( x \in B ) ) \} \\[4pt] &= \{x \in U | (x \notin A) \land (x \notin B)\} \\[4pt] &= \{x \in U | (x \in \bar{A}) \land (x \in \bar{B})\} \\[4pt] &= \bar{A} \cap \bar { B } \end {align*} $$
یک اثبات استقرایی ساده را میتوان برای تأیید نسخههای تعمیمیافته از قوانین دمورگان برای مجموعهها به کار گرفت (در این آموزش فرض بر این است که همه مجموعهها زیرمجموعههایی از مجموعه جهانی بینامی هستند). با یک محاسبه ساده میتوان قانون دمورگان را برای سه مجموعه تأیید کرد:
$$ \large \begin {align*} \overline { A \cup B \cup C } & = \overline { ( A \cup B ) \cup C } \\[4pt] & = \overline { ( A \cup B ) } \cap \overline { C } \\[4pt] & = ( \overline { A } \cap \overline { B } ) \cap \overline { C } \\[4pt] & = \overline { A } \cap \overline { B } \cap \overline { C } \end {align*} $$
میتوانیم قوانین مشابهی را برای چهار مجموعه، پنج مجموعه و... به دست آوریم.
قضیه قانون دمورگان تعمیم یافته
برای هر عدد طبیعی $$ n ≥ 2 $$ و هر مجموعه $$ X_ 1 $$، $$ X_ 2 $$، ... و $$ X_ n $$، داریم:
$$ \large \overline { X _ { 1 } \cup X _ { 2 } \cup ... \cup X _ { n } } = \overline { X _ { 1 } } \cap \overline { X _ { 2 } } \cap ... \cap \overline { X _ { n } } $$
اثبات: اثبات را با استفاده از استقرا انجام میدهیم. در حالت پایه $$ n = 2 $$، گزاره $$ X_{1} ∪ X_{2} = X_{1} ∩ X_{n} $$ است. میخواهیم نشان دهیم که برای $$ n = k +1 $$ نیز صحیح است. $$ k$$ مجموعه $$ X_ 1 $$، $$ X_ 2$$، ... و $$ X_ { n + 1 } $$ را در نظر بگیرید. در نتیجه، داریم:
$$ \large \begin {align*} \overline { X _ { 1 } \cup X _ { 2 } \cup ... \cup X _ { k + 1 } } & = \overline { ( X _ { 1 } \cup X _ { 2 } \cup ... \cup X _ { k } ) \cup X _ { x + 1 } } \\[4pt] & = \overline { ( X _ { 1 } \cup X _ { 2 } \cup ... \cup X _ { k } ) } \cap \overline { X _ { k + 1 } } \\[4pt] & = ( \overline { X _ { 1 } } \cap \overline { X _ { 2 } } \cap ... \cap \overline { X _ { k } } ) \cap \overline { X _ { k + 1 } } \\[4pt] & = \overline { X _ { 1 } } \cap \overline { X _ { 2 } } \cap ... \cap \overline { X _ { k + 1 } } \end {align*} $$
در این محاسبه، مرحله دوم توسط قانون دمورگان برای دو مجموعه به دست میآید، در حالی که مرحله سوم از فرض استقرا به دست میآید.
عملگرهای جبر بولی مجموعه ها و منطق
درست همانطور که قوانین منطق به ما اجازه میدهد جبر را با فرمولهای منطقی انجام دهیم، قوانین نظریه مجموعهها به ما این امکان را میدهد که عملیات جبری را برای مجموعهها انجام دهیم. به دلیل ارتباط تنگاتنگ بین منطق و نظریه مجموعهها، جبر آنها بسیار مشابه است. جبر مجموعهها، مانند جبر منطق، جبر بولی است.
وقتی جورج بول کتاب خود را درباره منطق نوشت، واقعاً به اندازه منطق درباره نظریه مجموعهها نیز بود. در حقیقت، بول بین یک گزاره و مجموعه اشیاء که آن گزاره برای آنها صادق است، قائل نشده است و قوانین جبری و فرمولهای آن به همان اندازه در هر دو مورد اعمال میشود. به طور دقیقتر، اگر ما فقط زیرمجموعه برخی از مجموعههای جهانی $$U$$ را در نظر بگیریم، مطابق جدول زیر، بین نمادهای اساسی و عملکرد منطق گزاره و نمادها و عملیات خاص در نظریه مجموعهها، ارتباط مستقیمی وجود دارد.
| منطق | نظریه مجموعهها |
| $$\mathbb{T}$$ | $$U$$ |
| $$\mathbb{F}$$ | $$\emptyset$$ |
| $$p \land q$$ | $$A \cap B$$ |
| $$p \lor q$$ | $$A \cup B$$ |
| $$\neg p$$ | $$\overline{A}$$ |
هر فرمول یا محاسبه منطقی معتبر با متغیرهای گزارهای و نمادهای $$ \mathbb{T} $$، $$\mathbb{F} $$، $$ ∧ $$، $$∨ $$ و $$ ¬ $$ را میتوان با جایگذاری گزارهها در فرمول با زیرمجموعههای $$U$$ و جایگزینی نمادهای منطقی با $$ U$$، $$ ∅ $$، $$ \cap $$، $$ \cup $$ و عملگر مکمل به یک فرمول یا محاسبه در نظریه مجموعهها تبدیل کرد.
مشابه آنچه در منطق داریم، عملیات نظریه مجموعهها را میتوان ترکیب کرد و عبارت پیچیدهای مانند $$ (A∪C)∩ \overline{(B ∪ \overline{C} ∪ D)} $$ به دست آورد. همواره میتوان از پرانتز برای چنین عبارتهایی به منظور تعیین اولویت عملیات استفاده کرد. در غیاب پرانتزها، به حضور قواعدی نیاز داریم تا اولویت عملیات را تعیین کنیم. قوانین تقدم در جبر بولی مجموعهها مستقیماً از جبر بولی برای گزارهها به دست میآیند. وقتی اجتماع و اشتراک با هم و بدون پرانتز مورد استفاده قرار میگیرند، اشتراک بر اجتماع تقدم دارد.
علاوه بر این، وقتی چند عملگر با نوع مشابه و بدون پرانتز استفاده شود، از چپ به راست آنها را اعمال میکنیم (البته از آنجا که $$ \cup $$ و $$ \cap $$ هرو عملگرهایی شرکتپذیر هستند، واقعاً مهم نیست که از چپ به راست یا راست به چپ آنها را اعمال کنیم). برای مثال، $$ A ∪ B ∩ C ∪ D $$ به صورت $$(A ∪ ((B ∩ C)) ∪ D $$ محاسبه میشود. عملیات مکمل یک حالت خاص است. از آنجا که با یک خط روی عملوند مشخص میشود، هیچگونه سردرگمی وجود نخواهد داشت.
میتوان قوانین نظریه مجموعهها را به کار گرفت و عبارات پیچیده را سادهسازی کرد. (البته چنانکه رایج است، معنی «سادهسازی» تا حدی برای چشم بیننده است.) برای مثال، برای مجموعههای $$ X $$ و $$ Y $$، داریم:
$$ \large \begin {align*} ( X ∪ Y ) ∩ ( Y ∪ X ) & = ( X ∪ Y ) ∩ ( X ∪ Y ) \\[4pt] & = ( X ∪ Y ) \end {align*} $$
که در مرحله دوم، قانون خودتوانی، که بیان میکند $$ A ∩ A = A $$، با $$ A = X ∪ Y $$ اعمال میشود. برای عباراتی که از عمل مکمل استفاده میکنند، معمولاً سادهتر است که عملیات را به یک مجموعه تکی اعمال کرد، مثلاً $$ A $$، تا اینکه به فرمولی مانند $$ A ∩ B $$.
$$ \large A \cap \overline { B \cup \overline { A } } = A \cap ( \overline { B } \cap \overline { \overline { A } } )
= A ∩ (\overline{B} ∩ A) \\ \large = A ∩ (A ∩ \overline{B}) = (A ∩ A ) ∩ \overline { B } ) = A ∩ \overline { B } $$
به عنوان مثال آخر رابطه بین نظریه مجموعهها و منطق، عبارت مبتنی بر نظریه مجموعههای $$ A ∩ (A ∪ B) $$ و گزاره ترکیبی $$ p ∧ (p ∨ q) $$ را در نظر بگیرید (این دو متناظرند، زیرا برای هر $$ x $$، تساوی $$ x,x ∈ A∩(A∪B) ≡ (x ∈ A)∧((x ∈ A)∨(x ∈ B)) $$ را داریم. ممکن است بگویید که $$ A ∩ (A ∪ B) = A $$ به صورت شهودی واضح است.
به طور رسمی، این تساوی از این واقعیت ناشی میشود که $$p ∧ (p ∨ q) ≡ p$$، که ممکن است از نظر شهودی کمتر روشن باشد و اثبات جبری آن از قوانین منطق دشوار باشد. با وجود این، روش دیگری برای بررسی صحت تساوی منطقی وجود دارد؛ اینکه یک جدول درستی تهیه کنیم. جدول درستی $$ p ∧ (p ∨ q) $$ را در نظر بگیرید.
| $$p \land (p \lor q)$$ | $$p \lor q$$ | $$q$$ | $$p$$ |
| نادرست | نادرست | نادرست | نادرست |
| نادرست | درست | درست | نادرست |
| درست | درست | نادرست | درست |
| درست | درست | درست | درست |
این واقعیت که ستون اول و ستون آخر این جدول مشابه هستند، نشان میدهد که $$ p∧(p∨q)≡p $$. با در نظر گرفتن $$ p $$ به عنوان گزاره $$ x \in A $$ و $$ q $$ به عنوان گزاره $$ x \in B $$، نتیجه خواهیم گرفت که مجموعههای $$ A $$ و $$ A ∩ (A ∪ B) $$ اعضای یکسانی دارند و در نتیجه، برابرند.











یک سوال داشتم
علت عدم ارسال اطلاعات از نرم افزار می تواند باگ یا خطای برنامه نویسی باشد درست
برای فهمیدن خطا چکار باید کرد و چگونه متوجه خطا شویم
پیشاپیش از همکاری شما تشکر می کنم