توزیع و متغیر تصادفی رایلی (Rayleigh Distribution) — به زبان ساده

توزیع و متغیر تصادفی رایلی (Rayleigh Distribution)، به عنوان یکی از توزیع‌های آماری با مقادیر پیوسته (Continuous)، در استنباط آماری شناخته شده است. مقادیر این متغیر تصادفی، نامنفی است و در حالت خاص این توزیع شبیه یک توزیع کای ۲ با دو درجه آزادی است. در این نوشتار به بررسی توزیع و متغیر تصادفی رایلی خواهیم پرداخت و کاربردهای آن را بررسی خواهیم کرد. از این توزیع برای پدیده‌های فیزیکی مثلا برآورد خطای دستگاه MRI استفاده می‌شود.

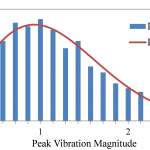
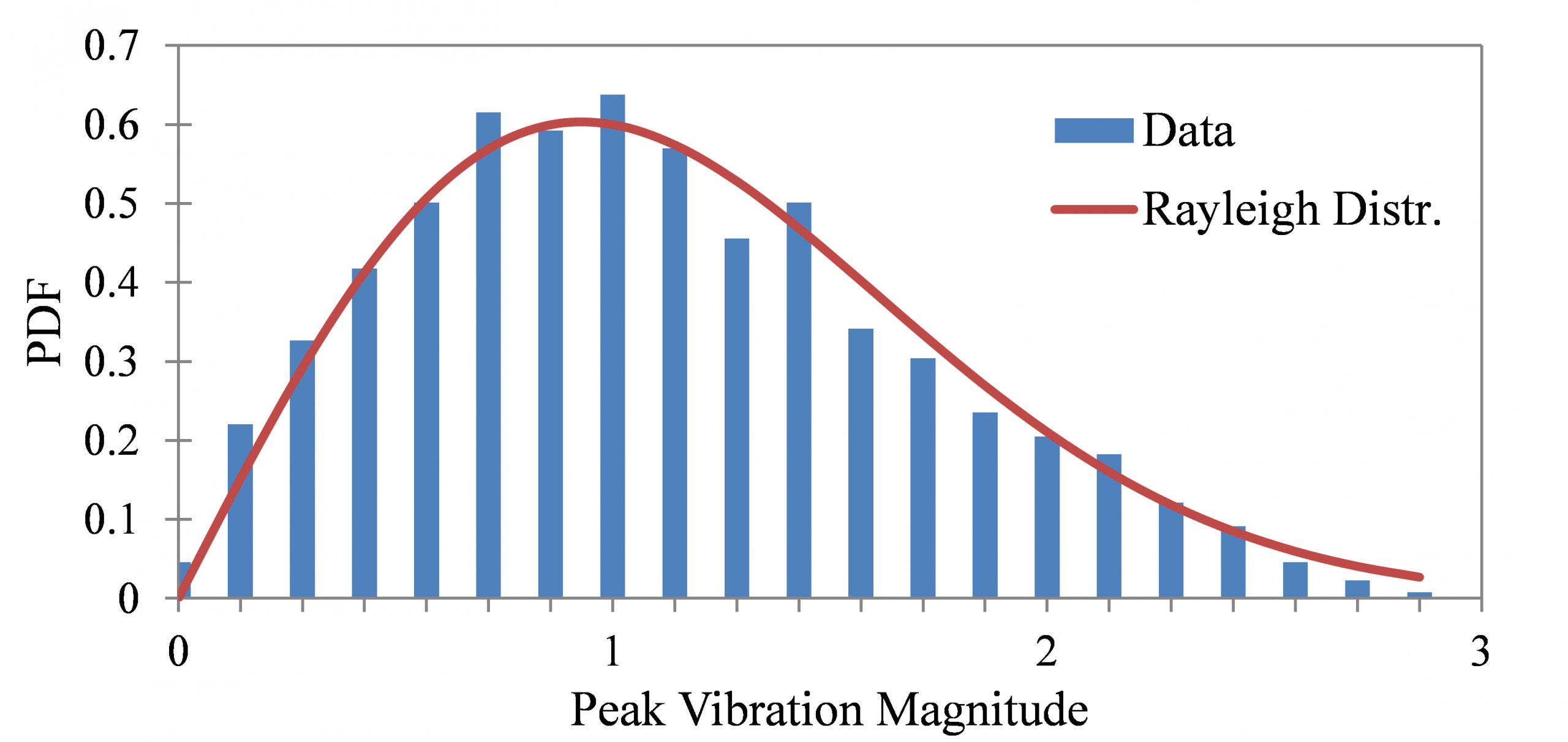
برای آشنایی بیشتر با مفاهیم مربوط به توزیع‌های آماری، بهتر است مطلب متغیر تصادفی، تابع احتمال و تابع توزیع احتمال را مطالعه کنید. همچنین مطالعه توزیع های آماری — مجموعه مقالات جامع وبلاگ فرادرس نیز خالی از لطف نیست.

توزیع و متغیر تصادفی رایلی

معمولا توزیع رایلی مربوط به متغیرهای تصادفی یا بردارهایی تصادفی است که مقدارشان با مولفه جهت بردار در ارتباط است. برای مثال، سرعت وزش باد به دو عامل (میزان سرعت و جهت) وابسته است. تصور کنید که هر یک از این عامل‌ها «ناهمبسته» (Uncorrelated) و دارای توزیع نرمال با میانگین صفر و واریانس یکسان باشند، آنگاه برآیند سرعت وزش باد (مقدار بردار سرعت) به کمک توزیع رایلی، شناخته می‌شود.

فیلم آموزش شبیه سازی متغیرهای تصادفی و وابسته در متلب در فرادرس

کلیک کنید

همچنین یک متغیر با مقادیر مختلط را در نظر بگیرید که قسمت موهومی و حقیقی آن مستقل از یکدیگر بوده و دارای توزیع نرمال هستند. میانگین این توزیع‌ها صفر و واریانس‌شان، برابر است. در این حالت قدرمطلق این مقدار حقیقی دارای توزیع رایلی خواهد بود. این توزیع به افتخار «لرد رایلی» (Lord Rayleigh) فیزیکدان انگلیسی، توزیع رایلی نامیده شده است.

تابع احتمال و توزیع رایلی

اگر متغیر تصادفی $$X$$ دارای تابع توزیع به فرم زیر باشد، توزیع رایلی نامیده می‌شود.

$$\large f(x;\sigma )={\frac {x}{\sigma ^{2}}}e^{-x^{2}/(2\sigma ^{2})},\quad x\geq 0$$

مقدار $$\sigma$$ را پارامتر مقیاس (Scale Parameter) برای این توزیع می‌گویند. در این حالت می‌نویسیم $$X\sim \operatorname{Rayleigh}(\sigma)$$ است و می‌خوانیم متغیر تصادفی $$X$$ دارای توزیع رایلی با پارامتر سیگما است.

توجه داشته باشید که تکیه‌گاه این متغیر تصادفی مقادیر نامنفی است. در تصویر زیر، نمودار این تابع چگالی به ازاء مقادیر مختلف پارامتر $$\sigma$$ ترسیم شده است. همانطور که مشاهده می‌کنید، این توزیع دارای چولگی زیاد به سمت راست است.

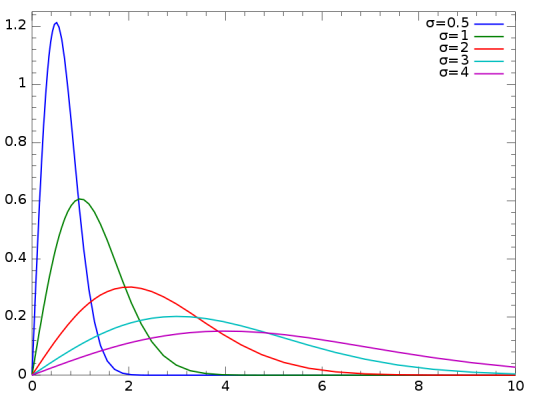
تابع توزیع احتمال تجمعی، برای توزیع متغیر تصادفی رایلی با پارامتر $$\sigma$$ به شکل زیر نوشته می‌شود.

$$\large F(x;\sigma )=1-e^{-x^{2}/(2\sigma ^{2})},\;\;x\in [0,\infty)$$

نمودار تابع توزیع احتمال تجمعی در تصویر زیر دیده می‌شود.

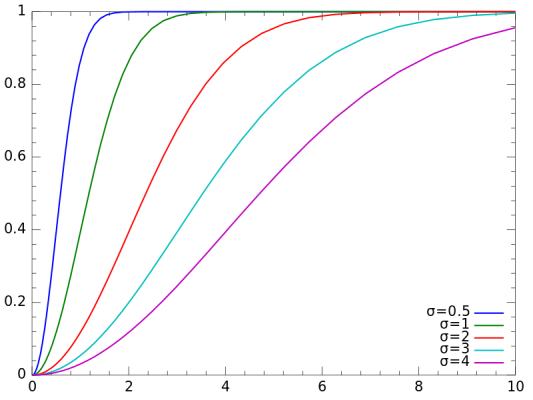
برای ارتباط این توزیع با بردارهای تصادفی دو بُعدی $$Y=(U,V)$$، حالتی را در نظر بگیرید، که هر یک از آن‌ها دارای توزیع نرمال با میانگین صفر و واریانس برابر هستند.

$$\large {\displaystyle f_{U}(x;\sigma )=f_{V}(x;\sigma )={\frac {e^{-x^{2}/(2\sigma ^{2})}}{\sqrt {2\pi \sigma ^{2}}}}}$$

مولفه $$X$$ را طول بردار $$Y$$ در نظر بگیرید. به این ترتیب خواهیم داشت:

$$\large {\displaystyle X={\sqrt {U^{2}+V^{2}}}}$$

آنگاه تابع توزیع تجمعی متغیر تصادفی $$X$$ به صورت زیر نوشته خواهد شد.

$$\large {\displaystyle F_{X}(x;\sigma )=\iint _{D_{x}}f_{U}(u;\sigma )f_{V}(v;\sigma )\,dA,}$$

که در آن $$D_x$$ دیسکی است که به صورت

$$\large {\displaystyle D_{x}=\left\{(u,v):{\sqrt {u^{2}+v^{2}}}<x\right\}}$$

تعریف می‌شود. با تبدیل این انتگرال به مختصات قطبی خواهیم داشت:

$$\large {\displaystyle F_{X}(x;\sigma )={\frac {1}{2\pi \sigma ^{2}}}\int _{0}^{2\pi }\int _{0}^{x}re^{-r^{2}/(2\sigma ^{2})}\,dr\,d\theta ={\frac {1}{\sigma ^{2}}}\int _{0}^{x}re^{-r^{2}/(2\sigma ^{2})}\,dr}$$

در نهایت برای پیدا کردن تابع چگالی متغیر تصادفی $$X$$ باید از تابع توزیع تجمعی برحسب $$x$$‌ مشتق بگیریم. بنا به «قضیه اساسی حسابان» (Fundamental Theorem of Calculus) می‌توان نوشت:

$$\large {\displaystyle f_{X}(x;\sigma )={\frac {d}{dx}}F_{X}(x;\sigma )={\frac {x}{\sigma ^{2}}}e^{-x^{2}/(2\sigma ^{2})},}$$

که همان تابع چگالی متغیر تصادفی رایلی است. البته این روش را برای بردارهای تصادفی بیش از دو بُعد نیز می‌توان به کار گرفت. همچنین متغیر تصادفی رایلی تعمیم یافته نیز برای زمانی که واریانس‌ها یکسان نباشند یا همبستگی بین دو ابعاد وجود داشته باشد، تعریف شده است.

همچنین می‌توان نشان داد که اگر متغیر تصادفی $$Y$$ دارای توزیع $$T$$ دو متغیره باشد، آنگاه $$X$$ دارای توزیع رایلی خواهد بود.

خصوصیات متغیر تصادفی رایلی

از آنجایی که گشتاور‌های متغیر تصادفی $$X$$ با توزیع رایلی به این صورت است:

$$\large {\displaystyle \mu _{j}=\sigma ^{j}2^{j/2}\,\Gamma \left(1+{\frac {j}{2}}\right)}$$

می‌توان امید ریاضی را به صورت زیر محاسبه کرد:

$$\large {\displaystyle \mu (X)=\sigma {\sqrt {\frac {\pi }{2}}}\ \approx 1.253\ \sigma }$$

نکته: توجه داشته باشید که منظور از $$\Gamma(z)$$‌، همان تابع گاما (Gamma Function) است.

واریانس متغیر تصادفی $$X$$ نیز برابر است با:

$$\large {\displaystyle \operatorname {var} (X)=\mu _{2}-\mu _{1}^{2}=\left(2-{\frac {\pi }{2}}\right)\sigma ^{2}\approx 0.429\ \sigma ^{2}}$$

ارتباط توزیع رایلی با توزیع‌های دیگر

فرض کنید دو متغیر تصادفی $$X$$ و $$Y$$ دارای توزیع نرمال با میانگین صفر و واریانس $$\sigma^2$$ باشند.  آنگاه به شرط استقلال $$X$$ و $$Y$$،

$$\large R=\sqrt{X^2+Y^2}\sim \operatorname{Rayleigh}(\sigma)$$

• اگر $$X$$ دارای توزیع کای ۲ با دو درجه آزادی باشد، آنگاه می‌توان آن را دارای توزیع رایلی با پارامتر ۱ در نظر گرفت.

$$\large X\sim \chi^2(2) \rightarrow X\sim \operatorname{Rayligh}(\sigma)$$

• اگر $$R\sim \mathrm {Rayleigh} (1)$$ آنگاه مربع $$R$$ دارای توزیع کای ۲ با ۲ درجه آزادی است.

$$\large R^{2}\sim \chi ^{2}(2)$$

• اگر متغیرهای تصادفی $$R_i$$ دارای توزیع رایلی با پارامتر $$\sigma$$ باشد، آنگاه مجموع آن‌ها دارای توزیع گاما (Gamma Distribution) است.

$$\large\left[Y=\sum _{i=1}^{N}R_{i}^{2}\right]\sim \Gamma (N,2\sigma ^{2})$$

• اگر متغیر تصادفی $$X$$ دارای توزیع نمایی (Exponential Distribution) باشد. آنگاه ریشه دوم آن دارای توزیع رایلی است.

$$\large {\displaystyle X\sim \mathrm {Exponential} (\lambda )}\rightarrow {\displaystyle Y={\sqrt {X}}\sim \mathrm {Rayleigh} (1/{\sqrt {2\lambda }})}$$

• متغیر تصادفی با توزیع وایبل با پارامتر شکل $$k=2$$ دارای توزیع رایلی است. بطوری که $$\lambda=\sigma\sqrt{2}$$.

$$\large X\sim W(\lambda , 2) \rightarrow X\sim \operatorname{Rayleigh}(\dfrac{\lambda}{\sqrt{2}})$$

• فرض کنید متغیر تصادفی $$U$$ دارای توزیع یکنواخت در بازه $$(0,1)$$ باشد. آنگاه

$$\large {\displaystyle X=\sigma {\sqrt {-2\ln U}}\,}‍\sim \operatorname{Rayleigh}(\sigma)$$

از این ویژگی بخصوص برای تولید اعداد تصادفی از توزیع رایلی براساس توزیع یکنواخت (Uniform Distribution) استفاده می‌شود. به این ترتیب شبیه‌سازی از این توزیع را می‌توان به سادگی به کمک توزیع یکنواخت انجام داد.

کاربردهای توزیع رایلی

کاربرد متغیر تصادفی با توزیع رایلی را می‌توان در دستگاه‌های تصویربرداری رزونانس مغناطیسی (Magnetic Resonance Imaging) یا MRI یافت. از آنجا که تصاویر MRI به عنوان تصاویر پیچیده ثبت می‌شوند اما بیشتر اوقات به عنوان تصاویر برداری یا مقداری در نظر گرفته می‌شوند که نوفه‌ها (Noise) در این تصویر دارای توزیع رایلی است.

فیلم آموزش متغیرهای تصادفی پیوسته (رایگان) در فرادرس

کلیک کنید

همچنین از این توزیع برای توصیف داده‌های رژیم غذایی و نحوه تغذیه نیز استفاده می‌کنند، به این ترتیب ارتباط بین نوع تغذیه و واکنش‌های افراد و حتی حیوانات مورد بررسی قرار می‌گیرد.

خلاصه و جمع‌بندی

در این نوشتار به بررسی توزیع و متغیر تصادفی رایلی پرداختیم و خصوصیات آن را بررسی کردیم. تابع چگالی و توزیع به همراه امید ریاضی و واریانس آن نیز مورد بحث قرار گرفت. همچنین ارتباط این توزیع با توزیع‌های دیگر نیز معرفی شدند. کاربردهای مربوط به این توزیع آماری در فیزیک و دستگاه‌های فیزیکی به چشم می‌خورد.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های آمار و احتمالات
• آموزش آمار و احتمال مهندسی
• مجموعه آموزش‌های نرم‌افزار SPSS
• متغیر تصادفی و توزیع گامبل — به زبان ساده
• احتمال پسین (Posterior Probability) و احتمال پیشین (Prior Probability) — به زبان ساده
• تابع درستنمایی (Likelihood Function) و کاربردهای آن — به زبان ساده

^^