تخمین سری در ریاضی — به زبان ساده

در راستای معرفی مفاهیم مربوط به سری، آزمون‌های ریشه و انتگرال را معرفی کردیم. اما این آزمون‌ها تنها اطلاعاتی در مورد وضعیت همگرایی سری‌ها به ما داده و می‌گویند که یک سری همگرا یا واگرا است. از این رو در این مطلب قصد داریم تا در مورد روش‌های تخمین سری صحبت کنیم. البته پیشنهاد می‌کنیم قبل از مطالعه، مطالب آزمون ریشه، آزمون انتگرال و آزمون مقایسه سری را مطالعه فرمایید.

تخمین سری با آزمون‌های همگرایی

قبل از این که در مورد بدست آوردن مقدار یک سری صحبت کنیم، اجازه دهید تا همگرایی سری را توضیح دهیم. بدین منظور در ابتدا سری $$ \sum \limits _ { n = 1 } ^ \infty { { a _ n } } $$ را در نظر بگیرید. فرض کنید این سری به مقدار $$s$$ همگرا است. این همگرایی به معنای آن است که اگر دنباله $$ s _ n $$ را به صورت زیر در نظر بگیریم:

$$ { s _ n } = \sum \limits _ { i = 1 } ^ n { { a _ i } } $$

فیلم آموزش ریاضی مهندسی – مرور و حل مساله در فرادرس

کلیک کنید

در این صورت حاصل حد $$ s _ n $$ در بینهایت برابر است با:

$$ \large \mathop { \lim } \limits _ { n \to \infty } { s _ n } = s $$

عبارت فوق به معنای آن است که به ازای انتخاب‌ $$n‌$$های به اندازه کافی بزرگ، دنباله $$ s _ n $$ را می‌توان همگرا به $$s$$ در نظر گرفت. بنابراین یکی از روش‌های حدس زدن مقدار سری به این صورت است. در حقیقت می‌توان بخشی از سری را محاسبه کرده و آن را به عنوان تخمینی از پاسخ یک سری همگرا در نظر گرفت. بنابراین اگر مقدار $$n$$ به اندازه کافی بزرگ در نظر گرفته شود، می‌توان از تقریب زیر بهره برد.

$$ \large { s _ n } \approx s $$

روش فوق، یکی از روش‌های حدس زدن پاسخ یک سری محسوب می‌شود. اما سوالاتی که در مورد این روش مطرح می‌شود این است که چه زمانی می‌توان از این روش بهره برد و این‌که به ازای تعداد مشخصی از جملات، پاسخ تخمین زده شده به چه میزان نسبت به پاسخ دقیق خطا دارد؟ به منظور یافتن پاسخ این سوالات در ابتدا یک سری بینهایت را به صورت زیر در نظر بگیرید.

$$ \large \begin {equation} \sum \limits _ { i = 1 } ^ \infty { { a _ i } } = \sum \limits _ { i = 1 } ^ n { { a _ i } } + \sum \limits _ { i = n + 1 } ^ \infty { { a _ i } } \end{equation} $$

با نگاه به رابطه فوق می‌بینید که ترمِ اول همان $$s_n$$ است. عبارت دوم در رابطه فوق نیز تحت عنوان باقیمانده شناخته شده که آن را با $$ R _ n $$ نمایش می‌دهند. مقدار $$R_n$$ نشان‌دهنده خطای بین مقدار تخمینی ($$s_n$$) و مقدار واقعی ($$s$$) است. با این فرضیات رابطه فوق را می‌توان به صورت زیر بازنویسی کرد.

$$\large s = { s _ n } + { R _ n } $$

از این رو در عبارت فوق مقدار $$ { R _ n } $$ به ما میزان اختلاف بین مقدار حدس زده شده و مقدار واقعی سری را نشان می‌دهد. بدیهی است که ما نمی‌توانیم مقدار دقیق $$ { R _ n } $$ را تعیین کنیم. دلیل این امر آن است که مقدار دقیق $$ s $$ قابل تشخیص نیست. از این رو در ابتدا باید با استفاده از آزمون‌های مطرح شده، از وضعیت همگرایی سری اطمینان حاصل کرد. پس از تعیین وضعیت همگرایی می‌توان بهتر در مورد مقدار همگرایی تصمیم گرفت.

چندین آزمون به منظور بدست آوردن مقدار باقیمانده وجود دارد. در ادامه هریک از این روش‌ها به همراه مثال بررسی شده‌اند.

آزمون انتگرال

توجه داشته باشید که تنها زمانی می‌توان از این آزمون استفاده کرد که جملات سری مثبت و کاهشی باشند. آزمون انتگرال از این واقعیت ناشی می‌شود که می‌توان حد سری را به صورت مساحت زیر تابع $$ f \left ( n \right ) = { a _ n } $$ در نظر گرفت.

فیلم آموزش ریاضی مهندسی – مرور و حل سوالات کنکور دکتری در فرادرس

کلیک کنید

در ادامه خواهید دید که می‌توان با بدست آوردن حدود بالا و پایین باقیمانده، حدود بالا و پایینی برای $$s_n$$ نیز تعریف کرد. عکس این گزاره نیز صحیح است. در حقیقت می‌توان با محدود کردن مقدار سری در یک بازه، مقدار باقیمانده را نیز محدود کرد. در ابتدا باقیمانده را به صورت زیر باز می‌کنیم.

$$\large { R _ n } = \sum \limits _ { i = n + 1 } ^ \infty { { a_ i } } = { a _ { n + 1 } } + { a _ { n + 2 } } + { a_ { n + 3 } } + { a _ { n + 4 } } + \cdots $$

حال اگر مقدار $$x$$ را از $$ x = n + 1 $$ در نظر بگیریم، در این صورت می‌توان مطابق شکل زیر مستطیل‌هایی به عرض $$1$$ در نظر گرفته که ارتفاع سمت چپ مستطیل نیز برابر با مقدار تابع $$ f ( n ) $$ خواهد بود.

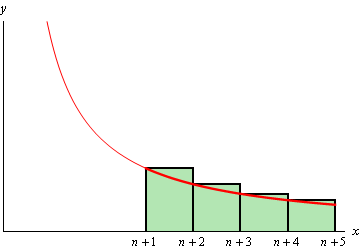
همان‌طور که در شکل فوق نیز مشخص شده، مقدار حاصل جمع مستطیل‌ها از مقدار انتگرال زیر نمودار بیشتر شده‌ است. بنابراین حد پایین مقدار باقیمانده را می‌توان به صورت زیر بیان کرد:

$$ \large \begin {equation} { R _ n } \ge \int _ { { \, n + 1 } } ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } \end {equation} $$

حال می‌توان نقطه شروع را از $$ \large x = n $$ در نظر گرفت. در این صورت می‌توان عرض مستطیل‌ها را برابر با $$1$$ در نظر گرفته و نقاط سمت راست را برابر با ارتفاع مستطیل‌ها فرض کرد. در این صورت مساحت مستطیل‌ها کمتر از مساحت زیر منحنی خواهد بود.

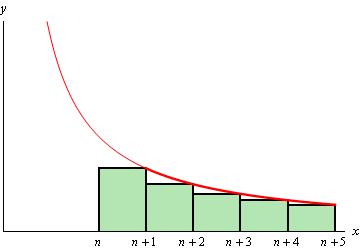
هم‌چنین حد بالای باقیمانده نیز برابر خواهد بود با:

$$ \large \begin {equation} { R _ n } \le \int _ { { \, n } } ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } \end {equation} $$

با توجه به حدود بدست آمده، مقدار باقیمانده در بازه زیر قرار خواهد داشت.

$$\large \int _ { { \, n + 1 } } ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } \le { R _ n } \le \int _ { { \, n }} ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } $$

بنابراین با محاسبه دو انتگرال فوق می‌توان محدوده‌ای از مقدار باقیمانده را یافت. حال به منظور تخمین سری، از رابطه زیر استفاده می‌کنیم (این رابطه در بالا توضیح داده شده).

$$ \large s = { s _ n } + { R _ n } $$

در این مرحله با استفاده از نامساوی $$ \begin {equation} { R _ n } \ge \int _ { { \, n + 1 } } ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } \end {equation} $$ می‌توان حد پایین $$s$$ را به صورت زیر بیان کرد:

$$ \large s = { s _ n } + { R _ n } \ge { s _ n } + \int _ { { \, n + 1 } } ^ { { \, \infty } }{ { f \left ( x \right ) \, d x } } $$

به همین صورت حد بالای $$s$$ نیز برابر است با:

$$ \large s = { s _ n } + { R _ n } \le { s _ n } + \int _ { { \, n } } ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } $$

با ترکیب این حدود، بازه $$s$$ برابر می‌شود با:

$$ \large \boxed { \begin{equation} { s _ n } + \int _ { { \, n + 1}}^{{\,\infty }}{{f\left( x \right) \, d x } } \le s \le { s _ n } + \int _ { { \, n } } ^ { { \, \infty } } { { f \left ( x \right ) \, d x } } \end{equation}} $$

با بدست آمدن مقادیر بالا و پایین سری می‌توان میانگین این حدود را به عنوان تخمینی برای سری در نظر گرفت. البته مقدار بدست آمده دقیق نخواهد بود و تنها تخمینی از مقدار سری محسوب می‌شود.

مثال ۱

با استفاده از $$ 15 $$ جمله اول، مقدار سری $$ \displaystyle \sum \limits _ { n = 1 } ^ \infty { \frac { 1 } { { { n ^ 2 } } } } $$ را بیابید. فرض کنید پاسخ دقیق این سری برابر با $$ 1.644934068 $$ است.

فیلم آموزش ریاضی مهندسی در فرادرس

کلیک کنید

$$ 15 $$ جمله اول به معنای در نظر گرفتن $$n=15$$ است. حاصل جمع این جملات برابرند با:

$$\large { s _ { 1 5 } } = \sum \limits _ { i = 1 } ^ { 1 5 } {\frac { 1} { {{ i ^ 2 } }}} = 1.580440283 $$

همان‌طور که می‌بینید مقدار فوق به پاسخ اصلی نزدیک است، اما برابر با آن نیست. از طرفی با توجه به روابط بدست آمده، حدود بالا و پایین $$s$$ برابرند با:

$$\large \int _ { { \,15 } } ^ { { \, \infty } } { { \frac { 1 } { { { x ^ 2 } } } \, d x } } = \frac {1 }{ { 1 5 }}\hspace{0.25in}\hspace{0.25in}\hspace{0.25in}\int_{{\,16 } } ^ { { \, \infty } } { { \frac{1}{{{ x ^2 } }}\,dx}} = \frac{1}{{16}} $$

بنابراین مقدار $$s$$ در بازه زیر قرار می‌گیرد:

$$\large \begin {align*}1.580440283 + \frac{1}{{16}} \le & s \le 1.580440283 + \frac{1} { { 15 } } \\ 1.642940283 \le & s \le 1.647106950 \end{align*} $$

از طرفی با میانگین‌گیری از حدود نامساوی فوق، مقدار $$s$$ برابر می‌شود با:

$$\large s \approx 1.6450236165 $$

همان‌طور که می‌بینید با استفاده از آزمون انتگرال، مقدار بدست آمده، به پاسخ اصلی بسیار نزدیک است. بنابراین با روش آزمون انتگرال به منظور پیش‌بینی مقدار سری آشنا شدید. در ادامه در مورد استفاده از روش آزمون مقایسه برای تخمین مقدار سری بحث خواهیم کرد.

آزمون مقایسه

دقت پاسخ بدست آمده وابسته به روش استفاده از آزمون مقایسه است. در ابتدا اجازه دهید تا این آزمون را مرور کنیم. از این رو تصور کنید که سری ‌هم‌چون $$ \sum { { a _ n } } $$ داده شده و با استفاده از آزمون مقایسه، همگرایی آن اثبات شده است. بنابراین سری هم‌چون $$ \sum { { b _ n } } $$ یافته شده که به ازای تمامی مقادیر $$n$$، مقدار $$ a _ n $$ کمتر از $$ b _ n $$ است. توجه داشته باشید که تمامی جملاتِ $$ a _ n $$ و $$ b _ n $$ باید مثبت باشند.

هدف از آزمون مقایسه، تعیین بیشترین خطای ممکن بین دو مقدارِ $$ { s _ n } = \sum \limits _ { i = 1 } ^ n { { a _ i } } $$ و پاسخِ واقعی $$ s = \sum _ { i = 1 } ^ { \infty } a _ i $$ است. در این روش نیز از مفهوم باقیمانده (یا همان خطا) به منظور تخمین مقدار سری استفاده می‌کنیم. باقیمانده‌‌های دو سری را به صورت زیر نشان می‌دهیم.

$$ { R _ n } = \sum \limits _ { i = n + 1 } ^ \infty { { a _ i } } \hspace {0.25in} \hspace{0.25in}\hspace{0.25in} { T_ n } = \sum \limits _ { i = n + 1 } ^ \infty { { b _ i } } $$

با توجه به نامساوی $$ { a _ n } \le { b _ n } $$، نامساوی زیر را نیز می‌توان برای باقیمانده‌ها بیان کرد:

$$ { R _ n } \le { T _ n } $$

معمولا در هنگام استفاده از این روش، تحلیل ترم $$ b _ n $$ راحت بوده، از این رو می‌توان مقداری مناسب را برای عدد $$T_n$$ حدس زد. دقیقا همانند آزمون انتگرال، با تحلیل مقدار مساحت نیز می‌توان حد بالای $$T_n$$ را بدست آورد. بنابراین نهایتا حد بالا و پایین $$T_n$$ برابرند با:

$$ \large \boxed { { R _ n } \le { T _ n } \le \int _ { { \, n } } ^ { \infty } { { g \left ( x \right ) \, d
x } } \hspace {0.25in} \hspace {0.25in} {\mbox{where }} g \left ( n \right ) = { b _ n }} $$

از رابطه فوق می‌توان دریافت که بیشترین خطای ممکن برای $$ R _ n $$ برابر با انتگرال $$ \int _ { { \, n } } ^ { \infty }{{g\left( x \right)\,dx}} $$ است.

مثال ۲

با استفاده از $$n=15$$، حاصل سری زیر را بدست آورید.

$$ \large \displaystyle \sum \limits _ { n = 0 } ^ \infty { \frac { { { 2^ n } } } { { { 4 ^ n } + 1 } } } $$

فیلم آموزش ریاضیات مهندسی – حل سوالات کنکور ارشد و دکتری در فرادرس

کلیک کنید

در ابتدا باید شرایط استفاده از آزمون مقایسه را برای این سری چک کنیم. بدین منظور می‌توان گفت:

$$ \large \frac { { { 2 ^n } }} { {{ 4 ^ n } + 1}} \le \frac { {{ 2 ^n } }} { { { 4 ^ n } }} = {\left( {\frac{1}{2}} \right)^n} $$

بنابراین می‌توان از سری $$ \sum \limits _ { n = 0 } ^ \infty { { { \left ( { \frac { 1 } { 2 } } \right ) } ^ n } }$$ به عنوان سری مقایسه استفاده کرد. این سری، یک سری هندسی با $$ \left| r \right| = \frac { 1 } { 2 } < 1 $$ است. از طرفی تخمین مدنظر برای این سری برابر است با:

$$\large { s _ {15 } } = \sum \limits _ { n = 0 } ^ {15} {\frac{{{2^ n }} }{ {{4^ n} + 1}}} = 1.383062486 $$

حال هدف، پاسخ به این سوال است که مقدار بدست آمده در بالا تا چه اندازه به مقدار واقعی نزدیک است؟ بدین منظور در ابتدا نامساوی فوق را به صورت زیر می‌نویسیم.

$$\large { R _ {15}} \le { T _ {15}} = \sum \limits _ { n = 16 } ^ \infty { { { \left ( {\frac {1} {2} } \right ) } ^ n } } $$

نامساوی فوق نشان دهنده حد بالای خطای بین مقدار حدس زده شده و مقدار واقعی است. با توجه به این که سری دوم یا $$b_n$$ یک سری هندسی است، لذا می‌توان مقدار دقیق آن را بدست آورد. از طرفی این سری به صورت زیر قابل بخش شدن است.

$$\large \sum \limits _ { n = 0 } ^ \infty { { { \left( {\frac { 1 }{ 2 }} \right ) }^ n } } = \sum \limits_{n = 0}^{15} {{{\left( {\frac{1} { 2}} \right)} ^ n } } + \sum \limits _ {n = 16} ^ \infty {{{\left( {\frac{1}{2}} \right) } ^ n }} $$

با توجه به مفهوم سری هندسی، عبارت فوق را می‌توان به صورت زیر بیان کرده و مقدار $$T_n$$ را بدست آورد.

$$\large \begin{align*}\sum \limits_{n = 16} ^ \infty {{{\left( {\frac{1}{2}} \right)}^n}} & = \sum\limits _ { n = 0}^\infty {{{\left( {\frac{1}{2}} \right)}^n}} - \sum \limits_{n = 0} ^ { 15 } { { { \left( { \frac { 1} { 2 }} \right)}^n}} \\ & = \frac{1}{{1 - \left ( { \frac{1}{2}} \right ) } } - 1.999969482\\ & = 0.000030518\end{align*} $$

مقدار بدست آمده در بالا بیشترین اختلاف ممکن بین مقدار باقیمانده و مقدار واقعی است. از طرفی مقدار دقیق این سری برابر است با:

$$\large \sum \limits _ { n = 0 } ^ \infty { \frac{ { { 2 ^ n}}}{{ { 4 ^ n} + 1}}} = 1.383093004 $$

همان‌طور که می‌بینید پاسخ تخمینی و مقدار دقیق، با دقت قابل قبولی به یکدیگر نزدیک هستند.

آزمون سری‌های متناوب

در دو روشی که در بالا بیان شد، سری‌هایی را می‌توانستیم حدس بزنیم که جملات آن‌ها مثبت بودند؛ اما اگر یک سری دارای جملات منفی باشد، استفاده از روش‌های بالا با مشکل مواجه خواهد شد. تنها یک آزمون وجود دارد که می‌توان از آن برای سری‌های با جملات منفی نیز استفاده کرد. این آزمون تحت عنوان آزمون سری متناوب شناخته می‌شود. در این حالت سری متناوبی همچون $$ \sum { { a _ n } = \sum { { { \left ( { - 1} \right ) }^ n } { b _ n } } } $$ را در نظر بگیرید که هدف تخمین مقدار آن است. توجه داشته باشید که دنباله $$ { b _ n } \ge 0 $$ کاهشی بوده و مقدار آن به ازای تمامی مقادیر $$n$$ مثبت است.

با استفاده از این آزمون نیز می‌توان فهمید که مقدار واقعی سری به چه میزان به جمع جزئی $$s_n$$ نزدیک است. همانند دو آزمون بالا در این آزمون نیز باقیمانده $$R_n$$ نشان دهنده میزان خطا نسبت به مقدار حدس زده شده است. بر مبنای آزمون سری متناوب می‌توان گفت که به ازای هر مقداری از $$n$$، مقدار $$s$$ بین دو مقدار $$s_n$$ و $$ s _ { n + 1 } $$ قرار می‌گیرد. بنابراین می‌توان نامساوی زیر را برای $$s$$ بیان کرد:

$$\large \left| { s - { s _n } } \right| \le \left| { { s _ { n + 1 } } - { s _ n } } \right| = { b _ { n + 1 } } $$

از طرفی مقدار باقیمانده برابر با اختلاف جمع جزئیِ $$s_n$$ و $$s$$ در نظر گرفته شده بود؛ لذا مقدار باقیمانده یا همان خطا را می‌توان با استفاده از این آزمون به صورت زیر بیان کرد:

$$ \boxed { \left| { { R_ n } } \right| = \left| { s - { s _ n } } \right| \le { b _ { n + 1 } } } $$

دلیل استفاده از قدر مطلق این است که نمی‌توان به طور دقیق تشخیص داد که مقدار حدس زده شده بیشتر یا کمتر از مقدار واقعی است.

مثال ۳

با استفاده از $$n=15$$ مقدار سری زیر را با استفاده از آزمون سری متناوب تخمین بزنید. فرض کنید مقدار دقیق این سری برابر با $$−0.8224670336$$ است.

$$ \large { \displaystyle \sum \limits _ { n = 1 } ^ \infty { \frac { { {{ \left ( { - 1 } \right)} ^ n } } } { { { n ^ 2 } } } } } $$

در ابتدا $$15$$ جمله اول سری را به صورت زیر محاسبه می‌کنیم.

$$ \large { s _ { 15 } } = \sum \limits _ { n = 1 } ^ {15} {\frac{{{{\left( { - 1} \right)}^n}}}{{{ n^ 2 } } }} = - 0.8245417574 $$

با فرض این‌که مقدار حدس زده شده برابر با عدد بالا باشد، آزمون ریشه به ما می‌گوید که بیشترین خطای ممکنِ این حدس برابر با عدد زیر خواهد بود.

$$ \large \left| { { R _ { 15 } } } \right | = \left | { s - { s _ { 15 } } } \right| \le {b_{16}} = \frac {1} { { { { 16 } ^ 2} } } = 0.00390625 $$

در صورت سوال مقدار دقیق این سری داده شده است؛ لذا خطای واقعی برابر است با:

$$ \large \left| { { R _ {15} } } \right| = \left| { s - { s _ {15}}} \right| = 0.0020747238 $$

آزمون نسبت

در این قسمت آخرین آزمون ارائه شده در این مطلب را توضیح خواهیم داد. توجه داشته که این آزمون در مواردی قابل استفاده است که تمامی جملات عمومی دنباله، مثبت باشند. در ابتدا باید یاد‌آوری کنیم که به منظور اثبات همگرایی دنباله با استفاده از آزمون نسبت، حد زیر محاسبه می‌شود:

$$ \large L = \mathop { \lim } \limits _ { n \to \infty } \left| { \frac { { { a_ { n + 1 } } }} { {{ a _ n } }} } \right| $$

فیلم آموزش ریاضی عمومی ۲ – مرور و حل تمرین در فرادرس

کلیک کنید

در صورتی که مقدار $$L$$ کمتر از $$1$$ باشد، سری فوق نیز همگرا خواهد بود. در این روش نیز همانند روش‌های قبل از $$R_n$$ به منظور میزان دقیق بودن جمعِ جزئیِ $$s_n$$ استفاده خواهیم کرد. بدین منظور در ابتدا دنباله زیر را محاسبه می‌کنیم.

$$ \large { r _n } = \frac { { {a _ { n + 1 } } } }{ {{ a _ n }}} $$

با بدست آوردن این دنباله، یکی از دو حالت زیر رخ خواهد داد.

اگر $$ \left\{ { {r _ {n } } } \right\} $$ یک دنباله کاهشی بوده و $$ {r_{n + 1}} < 1 $$ باشد در این صورت حد بالای $$R_n$$ برابر است با:

$$\large \begin {align*} { R _ n } \le \frac { { { a _ {n + 1} } } } { { 1 - { r _ { n + 1 } } } } \end {align*} $$

اگر $$ \left\{ { { r _ { n} } } \right\} $$ دنباله‌ای افزایشی باشد، در این صورت حد بالای $$R_n$$ برابر است با:

$$\large { R _ n } \le \frac { { { a _{ n + 1 } } } } { { 1 - L } } $$

اثبات

در ابتدا سری باقیمانده را به صورت زیر باز می‌کنیم.

$$\large \begin{align*} \large { R _ n } = \sum \limits _ { i = n + 1 } ^ \infty { { a _ i } } & = { a _ { n + 1 } } + { a _ { n + 2}} + {a_{n + 3}} + {a_{n + 4}} + \cdots \\ & = {a_{n + 1}}\left( {1 + \frac { { { a _ { n + 2 } } } }{ { { a _ { n + 1 } }}} + \frac{{{a_{n + 3}}}}{{{ a _ { n + 1} } }} + \frac{{{a _ { n + 4 } } } } { {{ a _ { n + 1 } } } } + \cdots } \right)\end{align*} $$

عبارت فوق را می‌توان به دو شکل زیر نیز بازنویسی کرد:

$$\large \begin{align*} {R _ n } & = { a _ { n + 1 } } \left ( { 1 + \frac { { { a _ { n + 2 } } } } {{ {a _ { n + 1 } } } } + \frac { { { a _ { n + 3 } }} } { {{ a _ { n + 1 } } } } \frac { { { a _{ n + 2 } } } } { { { a _ { n + 2 } } } } + \frac { { { a _ { n + 4 } } }} { { { a _ { n + 1}}}}\frac { {{a _ { n + 2 } } }} { { { a _ { n + 2 } } }}\frac{{{a_{n + 3}}}}{{{a_{n + 3}}}} + \cdots } \right)\\ & = {a_{n + 1}}\left( {1 + \frac{{{a_{n + 2}}}}{{{a_{n + 1}}}} + \frac{{{a_{n + 2}}}}{{{a_{n + 1}}}}\frac{{{a_{n + 3}}}} { { {a _ { n + 2}}}} + \frac{{{a_{n + 2}}}}{{{ a _ { n + 1}}}}\frac { { {a_{n + 3}}}}{{{ a _ { n + 2}}}}\frac{ { {
a_{n + 4}}}}{{{ a _{ n + 3}}}} + \cdots } \right) \end{align*}$$

حال با توجه به رابطه استفاده شده برای $$r_n$$، عبارت $$R_n$$ را می‌توان به صورت زیر بیان کرد:

$$\large \begin{align*} { R _ n } = {a_{n + 1}}\left( {1 + {r_{n + 1}} + {r_{n + 1}}{ r _ { n + 2 } } + { r _ { n + 1}} { r _ {n + 2 } } { r _ { n + 3 } } + \cdots } \right) \end{align*}$$
رابطه ۱

به منظور اثبات قسمت اول (کاهشی بودن $$ \left\{ { { r _ { n }}} \right\}$$)، مقدار باقیمانده را می‌توان به صورتی نوشت که در نامساوی زیر برقرار باشد.

$$ \large \begin{align*} { R _ n } & = {a_{n + 1}}\left( {1 + {r_{n + 1}} + {r_{n + 1}}{ r _{ n + 2 } } + {r_{n + 1}} { r _ {n + 2}}{r_{n + 3}} + \cdots } \right)\\ & \le {a_{n + 1}}\left( {1 + {r_{n + 1}} + r_{n + 1}^2 + r_{n + 1}^3 + \cdots } \right)\\ & = {a_{n + 1}}\sum\limits _ { k = 0} ^ \infty {r_{n + 1 } ^ k } \end{align*} $$

سری بدست آمده در بالا، سری‌ هندسی محسوب می‌شود. هم‌چنین با توجه به نامساوی $$ \large \begin{align*} { r _ { n + 1 } } < 1 \end{align*} $$، مقدار سری فوق برابر خواهد بود با:

$$\large \sum _ { k = 0 } ^ { \infty } r _ { n + 1 } ^ { k } = \frac { 1 } { 1-r _ { n + 1 } } $$

بنابراین نامساوی فوق نیز به صورت زیر قابل بیان است.

$$ \large { R _ n } \le \frac { { { a _ { n + 1 } } }} {{ 1 - { r _ { n + 1}}}} $$

به منظور اثبات حالت افزایشی بودن $$ \large \left\{ { { r _ { n} } } \right\} $$، می‌دانیم که حد زیر برقرار است.

$$ \large \mathop { \lim } \limits _ { n \to \infty } \left| {{ r _ n } } \right| = \mathop {\lim }\limits _ { n \to \infty } \left| {\frac { { { a _ { n + 1 }} }} { {{ a _ n }}}} \right| = L $$

با توجه به افزایشی بودن دنباله $$ \large \left\{ { { r _ { n } } } \right\} $$ و حد آن در بینهایت می‌توان نامساوی $$ { r _ n } < L $$ را برای تمامی $$n$$ها عنوان کرد. با اعمال کردن این نامساوی در رابطه ۱، داریم:

$$\large \begin{align*}{R_n} & = { a _ { n + 1 } } \left ( {1 + { r _ { n + 1}} + { r _ { n + 1} } { r _ { n + 2}} + {r_{n + 1} } { r _ { n + 2 } } { r _ { n + 3 } } + \cdots } \right)\\ & \le { a _ { n + 1 } } \left( {1 + L + { L ^ 2 } + {L^3} + \cdots } \right)\\ & = { a _{ n + 1} } \sum \limits_{k = 0}^\infty {{ L ^ k} } \end{align*}$$

همانند حالت قبل در این حالت نیز سری $$ \sum _ { k = 0 } ^ { \infty } L ^ { k } = \frac { 1 } { 1-L } $$ هندسی است. بنابراین نامساوی زیر قابل بیان خواهد بود.

$$ \large { R _n } \le \frac {{ { a _ { n + 1 } } } } { { 1 - L}} $$

مثال ۴

با استفاده از $$n=15$$، مقدار سری $$ \displaystyle \sum \limits _ { n = 0 } ^ \infty {\frac { n } { { { 3 ^ n } } }} $$ را تخمین بزنید.

فیلم آموزش ریاضی عمومی ۲ در فرادرس

کلیک کنید

در ابتدا می‌توان با استفاده از آزمون نسبت ثابت کرد که سری فوق همگرا است.

$$ \large L = \mathop { \lim } \limits _ { n \to \infty } \left| { \frac { { n + 1 } } { {{ 3 ^ {n + 1 } } } } \, \, \frac { { { 3 ^ n } } } {n}} \right| = \mathop {\lim }\limits_{n \to \infty } \frac { { n + 1}}{ { 3 n }} = \frac { 1 } {3} < 1$$

از طرفی جمع جزئی یا همان مقدار حدسی برابر است با:

$$\large {s_{15}} = \sum\limits_{n = 0 } ^ {15} {\frac{n}{{{ 3 ^n } } }} = 0.7499994250 $$

به منظور حدس زدن بیشترین خطا، در ابتدا باید دنباله زیر را تشکیل دهیم.

$$\large { r _ n } = \frac{{n + 1}}{ { { 3^ { n + 1}}}}\,\,\frac{{{3^n}}}{n} = \frac{{n + 1}}{{3n}} = \frac { 1 } { 3 }\left( {1 + \frac{1}{n}} \right) $$

اگر تابعی مطابق با دنباله فوق تشکیل داده و از آن مشتق بگیریم، متوجه خواهیم شد که این تابع نزولی است. در ادامه این مشتق‌گیری انجام شده است.

$$ \large f \left ( x \right ) = \frac { 1} { 3 } \left( {1 + \frac { 1 } { x } } \right ) \hspace{0.25in} \Rightarrow \hspace{0.25in} f ^ {\prime} \left( x \right) = - \frac { 1 } { {3 { x ^ 2 } }} < 0 $$

بنابراین دنباله $$ f \left ( n \right ) = { r _ n } $$ همواره کاهش می‌یابد. هم‌چنین گفتنی است که در این مثال حاصل جمع جزئی نیز کمتر از $$1$$ است ($$ { r _ {16}} = \frac { 1 } { 3 } \left( {1 + \frac{1} { { 16 } } } \right) < 1$$).

بنابراین ماکزیمم خطای بین مقدار جزئی و پاسخ دقیق سری برابر است با:

$$ \large { R _ { 15 } } \le \frac { { { a _ { 16 } } } } { {1 - { r _ {16}}}} = \frac { { \frac{{16}}{{{3^{16}} } } } }{{1 - \frac{1}{3}\left( {1 + \frac{1}{{16}}} \right)}} = 0.0000005755187$$

عدد فوق نشان می‌دهد که حاصل جمعِ $$16$$ جمله اول، به پاسخ نهایی سری بسیار نزدیک است. در صورت علاقه‌مندی به مباحث مرتبط در زمینه ریاضی، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• سری همگرا و واگرا — از صفر تا صد
• آزمون مقایسه سری — به زبان ساده
• آزمون نسبت در سری - به زبان ساده

^^