آزمون ریشه در سری — به زبان ساده (+ دانلود فیلم آموزش رایگان)
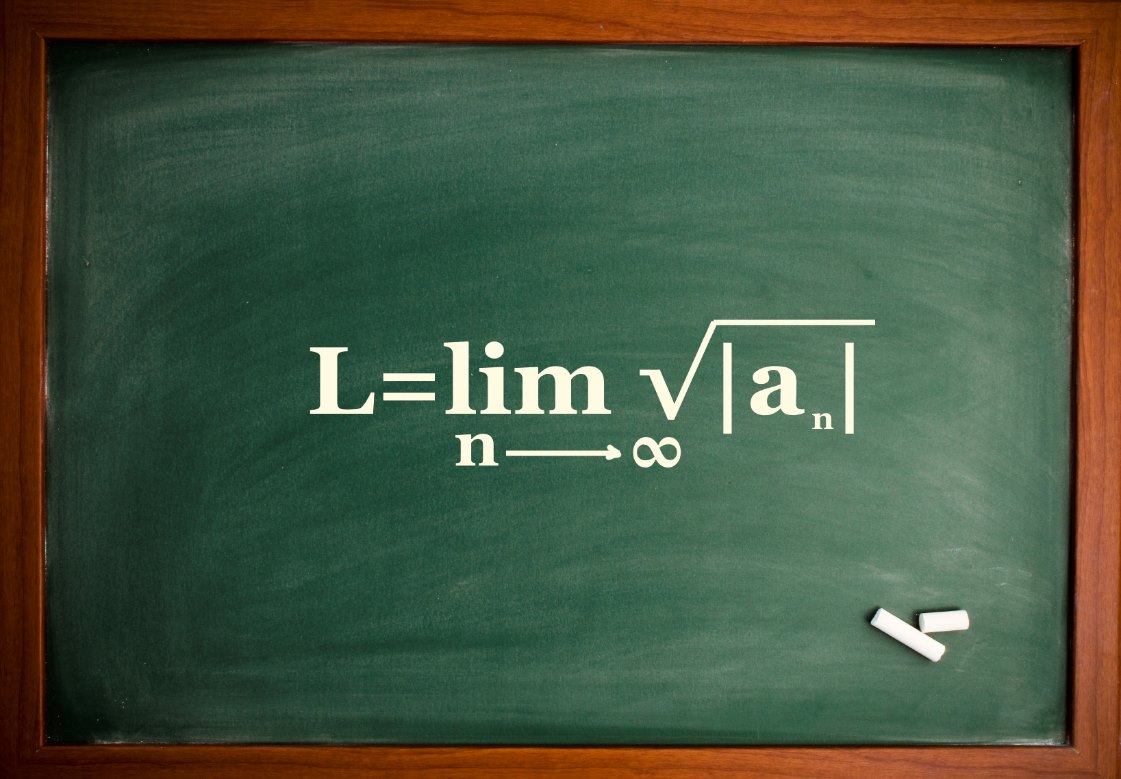
پیشتر در وبلاگ فرادرس مفاهیم مربوط به سری و روشهای تشخیص وضعیت همگرایی را مورد بررسی قرار دادیم. از این رو در این مطلب قصد داریم تا آزمونی جدید به منظور بررسی وضعیت همگرایی را مورد بررسی قرار دهیم. این آزمون تحت عنوان آزمون ریشه شناخته میشود. البته در صورت علاقهمندی میتوانید مطلب آزمون انتگرال را نیز مطالعه فرمایید.
آزمون ریشه
فرض کنید میخواهیم وضعیت همگرایی سری $$ \large \sum { { a _ n } } $$ را مشخص کنیم. در این صورت در ابتدا حد زیر را محاسبه میکنیم (این که مقدار $$n$$ از چه عددی شروع شود در کلیت مسأله تغییری ایجاد نخواهد کرد).
$$ \large L = \mathop { \lim } \limits _ { n \to \infty } \sqrt [ n \ \ \ ] { { \left| { { a _ n } } \right| } } = \mathop { \lim } \limits _ { n \to \infty } { \left| { { a _ n } } \right| ^ { \frac { 1 } { n} } } $$
بسته به این که عدد $$L$$ چه مقداری باشد، هریک از نتایج زیر را میتوان گرفت:
- اگر $$ \large L < 1 $$ باشد، آنگاه سری همگرای مطلق است.
- اگر $$ \large L > 1 $$ باشد، آنگاه سری واگرا است.
- اگر $$ \large L = 1 $$ باشد، آنگاه سری میتواند همگرای مطلق، همگرای مشروط یا واگرا باشد.
همانطور که در بالا نیز بیان شده، در حالتی که $$L=1$$ باشد نمیتوان با استفاده از آزمون ریشه، وضعیت سری را مشخص کرد. نکته بسیار مهم دیگر این است که اگر در آزمون نسبت مقدار $$L=1$$ بدست آید، در این صورت آزمون ریشه نیز همین نتیجه را به ما خواهد داد. یکی از عبارتهایی که در آزمون ریشه با آن مواجه خواهیم بود، در ادامه ارائه شده است.
$$ \large \mathop { \lim } \limits _ { n \to \infty } { n ^ { \frac { 1 } { n} } } = 1 $$
اثبات آزمون ریشه
در ابتدا میتوان سری را از مقدار $$ \large n=1 $$ در نظر گرفت. همچنین فرض بر این است که مقدار $$ L<1 $$ باشد. با توجه به فرض کمتر از ۱ بودن $$L$$، عددی همچون $$r$$ را میتوان در نظر گرفت که در نامساوی $$ \large 0 < r < 1 $$ صادق باشد. همچنین همانطور که در بالا نیز بیان شد، عدد $$L$$ در آزمون ریشه به صورت زیر بدست میآید.
$$ \large L = \mathop { \lim } \limits _ { n \to \infty } \sqrt[n \ \ \ ] { { \left| { { a _ n } } \right| } } = \mathop { \lim } \limits _ { n \to \infty } {\left| { { a _ n } } \right | ^ { \frac {1 } {n } } } $$
با توجه به فرض $$L<r$$ عددی همچون $$N$$ را میتوان در نظر گرفت به نحوی که به ازای مقادیر $$n>N$$ نامساوی زیر قابل نوشتن باشد.
$$ \large { \left| { { a _ n } } \right| ^ { \frac { 1 } { n } } } < r \hspace {0.5in} \Rightarrow \hspace {0.5in}\left| { { a _ n } } \right| < { r ^ n } $$
بنابراین سری $$ \large \sum\limits _ { n = 0 } ^ \infty { { r ^ n } } $$ یک سری هندسی محسوب میشود و با توجه به کمتر از ۱ بودن $$r$$ میتوان نتیجه گرفت که همگرا است. بنابراین با توجه به نامساوی $$ \large \left| { { a _ n } } \right| < { r ^ n } $$ و همچنین آزمون مقایسه سریها میتوان دریافت که سری زیر نیز همگرا است.
$$ \large \sum \limits _ { n = N } ^ \infty { \left| { { a _ n } } \right| } $$
از طرفی سری اصلی که هدف بررسی آن بود را میتوان به صورت زیر و در قالب دو سری بیان کرد.
$$ \large \sum \limits _ { n = 1 } ^ \infty { \left| { { a _n } } \right| } = \sum \limits _ { n = 1 } ^ { N - 1 } { \left| { { a _ n } } \right| } + \sum \limits _ { n = N } ^ \infty { \left| { { a _ n } } \right| } $$
ترم اول در رابطه فوق از تعداد معدودی جمله تشکیل شده لذا همگرا است. از طرفی در بالا نیز اثبات شد که سری $$ \large \sum \limits _ { n = N } ^ \infty { \left| { { a _ n } } \right| } $$ نیز همگرا است. بنابراین با همگرا بودن دو ترم سمت راست، میتوان نتیجه گرفت کل سری همگرا است.
همچنین در آزمون ریشه بیان شد که به ازای مقادیر $$ L > 1 $$، سری واگرا است. در ابتدا یادآوری میکنیم که منظور از $$L$$ مقدار زیر است.
$$ \large L = \mathop { \lim } \limits _ { n \to \infty } \sqrt [n \ \ \ ] { { \left| { { a _ n } } \right| } } = \mathop { \lim } \limits _ { n \to \infty } { \left| { { a_ n } } \right| ^ { \frac { 1} { n } } } $$
همچنین با توجه به نامساوی $$ \large L > 1 $$ مقداری از $$N$$ وجود خواهد داشت که به ازای $$ \large n \ge N $$ داریم:
$$ \large { \left| { { a _ n } } \right| ^ { \Large \frac { 1 } {n } } } > 1 \hspace {0.5in} \Rightarrow \hspace {0.5in} \left| { { a _ n } } \right| > { 1 ^ n } = 1 $$
همچنین اگر به ازای تمام مقادیر $$ \large n \ge N $$ گزاره $$\left| {{a_n}} \right| > 1$$ برقرار باشد، در این صورت میتوان گفت که حد دنباله در بینهایت عددی غیر صفر است. لذا میتوان نوشت:
$$ \large \mathop { \lim } \limits _ { n \to \infty } \left| { { a _ n } } \right| \ne 0 $$
با توجه به غیر صفر بودن دنباله در بینهایت میتوان گفت که سری $$\sum {{a_n}}$$ نیز واگرا خواهد بود. در ادامه برای نمونه ۳ سری معرفی شده که وضعیت همگرایی آنها نیز مشخص شده است.

مثال ۱
وضعیت همگرایی سری زیر را تعیین کنید.
$$ \large \sum \limits _ { n = 1 } ^ \infty { \frac { { { n ^n } } } { {{ 3 ^{1 + 2n}}}}} $$
حاصل حد ریشه $$n$$ام این تابع برابر است با:
$$ \large L = \mathop {\lim }\limits _ { n \to \infty } {\left| {\frac{{ { n ^n } } } { { { 3 ^ { 1 + 2 n } } } } } \right| ^ { \frac { 1 } { n } } } = \mathop {\lim }\limits_{n \to \infty } \frac { n } { { { 3 ^ { \frac { 1 } { n } + 2 } } } } = \frac {\infty } { { { 3 ^ 2 } } } = \infty > 1 $$
همانطور که میبینید مقدار حد بدست آمده بیشتر از ۱ بوده، بنابراین سری فوق واگرا خواهد بود.
مثال ۲
وضعیت همگرایی سری زیر را معین کنید.
$$ \large \sum \limits _ { n = 0 } ^ \infty { { { \left ( { \frac { { 5 n - 3 { n ^ 3} } } { { 7 { n ^ 3 } + 2 } } } \right ) } ^ n } } $$
حاصل حد جمله عمومی در بینهایت برابر است با:
$$ \large L = \mathop {\lim }\limits_{n \to \infty } {\left| {{{\left( {\frac { { 5 n - 3 { n ^ 3 } } } { { 7 { n ^ 3 } + 2 } } } \right)}^n}} \right|^{\frac { 1 } { n } } } = \mathop { \lim } \limits _ { n \to \infty } \left| { \frac{ { 5 n - 3 { n ^ 3 } } }{ { 7 { n^ 3 } + 2 } } } \right| = \left| {\frac { { - 3 } } { 7 } } \right| = \frac { 3 } { 7 } < 1 $$
بنابراین با استفاده از آزمون ریشه میتوان نتیجه گرفت که سری همگرا است.
مثال ۳
وضعیت همگرایی سری زیر را مشخص کنید.
$$ \large \sum \limits _ { n = 0 } ^ \infty { \left( {\frac { { 3 n + 1 } } { { 4 – 2 n } } } \right ) } ^ { 2 n } $$
همانند مثالهای ۱ و ۲ حد جمله عمومی در بینهایت را به صورت زیر محاسبه میکنیم.
$$ \large L = \mathop { \lim } \limits _ { n \to \infty } \sqrt [ n \ \ \ ] { { \left| { { a _ n } } \right|}} = \mathop {\lim }\limits_{n \to \infty } { \left| { { { \left( {\frac { { 3 n + 1 } } { { 4 - 2 n } } } \right ) } ^ { 2 n } } } \right|^{\frac { 1 } { n } } } = \mathop {\lim }\limits _ { n \to \infty } \left| { { { \left( {\frac { { 3 n + 1 } } { {4 - 2 n } } } \right)}^2}} \right| = {\left( { - \frac { 3 } { 2 } } \right ) ^ 2 } = \frac { 9 } { 4 } $$
احتمالا متوجه شدهاید که مهمترین مهارتی که به منظور استفاده از آزمون ریشه باید به آن مسلط باشید، محاسبه حد ترمهای توانی است. در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- همگرایی مطلق و همگرایی مشروط — به زبان ساده
- آزمون انتگرال -- به زبان ساده
- سری همگرا و واگرا — از صفر تا صد
- سری تیلور — از صفر تا صد
^^










