فرادرسانواع معادله ها در ریاضی — به زبان ساده
در آموزش‌های پیشین مجله فرادرس با معادله و تعریف آن آشنا شدیم. در این آموزش انواع معادله را معرفی می‌کنیم.
معادله چیست؟
در ریاضیات، معادله یک گزاره ریاضیِ تشکیل شده از یک نمادِ مساوی بین دو عبارت جبری است که دارای مقدار یکسان هستند.
به زبان ساده‌تر، معادله یک تساوی بین دو عبارت جبری است. شاید ابتدایی‌ترین و رایج‌ترین معادلات جبری در ریاضیات از یک متغیر تشکیل شده است. به‌عنوان مثال، $$ 5 x + 7 = 17 $$ معادله‌ای است که در آن، $$ 5 x + 7 $$ و $$17$$ دو عبارتی هستند که با علامت «مساوی» یا "=" با هم مساوی قرار داده شده‌اند. در یک معادله جبری، سمت چپ با سمت راست برابر است.
در اینجا، برای مثال، $$5x + 7$$ عبارت سمت چپ است که برابر است با عبارت $$24$$ در سمت راست.
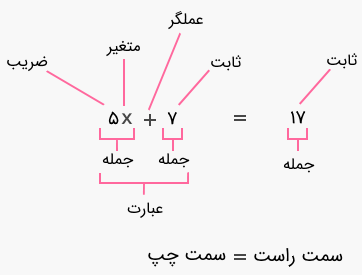
به‌عنوان مثال، $$5x + 6y – 10$$ را یک معادله درنظر نمی‌گیریم، زیرا علامت تساوی ندارد و می‌توانیم بگوییم تنها یک عبارت است. مطالعه جبر عمدتاً در مورد یادگیری حل انواع مختلف معادلات است.
انواع معادله ها
انواع مختلفی از معادلات وجود دارد که در بسیاری از زمینه‌های ریاضی قابل مشاهده‌اند. انواع معادله ها از همان تساوی که گفتیم پیروی می‌کنند و حل هریک از آن‌ها با توجه به نوعشان متفاوت است.
برای مثال، در جبر دو خانواده اصلی از معادلات رایج‌تر هستند: معادلات چندجملهای و از میان آن‌ها معادلات خطی. معادلات چندجملهای به شکل $$ p ( x ) = 0 $$ هستند که در آن، $$p$$ یک چندجملهای است. معادلات خطی به شکل $$ a x + b = 0 $$ هستند که در آن، $$ a $$ یک تابع خطی و $$b$$ یک بردار است. برای حل این معادلات از روش‌های الگوریتمی یا هندسی استفاده می‌شود که از جبر خطی یا تحلیل ریاضی به‌دست آمده‌اند.
در جبر همچنین معادلات کمتر شنیده شده‌ای مانند معادله دیوفانتین مطالعه می‌شود که در آن ضرایب و جواب‌ها اعداد صحیح هستند. حل این معادلات به طور کلی دشوار است.
در هندسه، از انواع معادله ها برای توصیف اشکال هندسی استفاده می‌شود. این معادلات، مانند معادلات ضمنی یا معادلات پارامتری، جواب‌های زیادی دارند. در آنجا به‌جای اینکه جواب‌ها صریحاً محاسبه شود یا آن‌ها را بشماریم که غیرممکن است، از معادلات برای مطالعه ویژگی‌های شکل ها استفاده می‌شود. این ایده آغازین هندسه جبری، حوزه مهمی از ریاضیات است.
معادلات دیفرانسیل نیز معادلاتی هستند که شامل یک یا چند تابع و مشتقات آن‌ها می‌شود. این معادله‌ها با یافتن عبارتی برای تابعی که مشتقات را شامل نمی‌شود، حل می‌شوند. معادلات دیفرانسیل برای مدل‌سازی فرایندهای واقعی در زمینه‌هایی مانند فیزیک، شیمی، زیست‌شناسی و اقتصاد به‌کار می‌روند.
معادلات دیفرانسیل برای مدل‌سازی سیستم‌هایی به کار می‌روند که به صورت پیوسته در حال تغییر هستند. اما اگر تغییر به‌جای آنکه پیوسته باشد، بهصورت گسسته اتفاق بیفتد، معادلات دیفرانسیل کاستی‌هایی خواهند داشت. در این صورت، از معادلات تفاضلی که دنباله‌هایی بازگشتی هستند استفاده می‌شود.
آنچه گفتیم، یک معرفی اجمالی از برخی معادلاتی بود که در ریاضیات وجود دارند. اما معمولاً آنچه را که در دوره دبیرستان یا ریاضیات پایه دانشگاهی در دسته انواع معادله ها قرار می‌دهند، معادلاتی از قبیل درجه اول، درجه دوم، درجه سوم، مثلثاتی، رادیکالی، نمایی و امثال این‌ها هستند که در ادامه آن‌ها را معرفی و مثال‌هایی را حل می‌کنیم.
معادله چندجملهای
معادله چندجملهای، همان‌گونه که نامش نشان می‌دهد، یک معادله است که در آن چندجمله‌ای‌های یک طرف تساوی هستند. یک معادله چندجملهای را می‌توان بهصورت زیر نوشت که در آن، $$P$$ یک چندجملهای برحسب $$ x $$ است:
$$ \large P ( x ) = 0 $$
معادله درجه اول
معادله درجه اول یا همان معادله خطی یک معادله درجه اول جبری است. در معادله خطی، هر جمله یک عدد ثابت یا حاصل‌ضرب یک عدد ثابت و یک متغیر است. اگر معادله دو متغیر داشته باشد، نمودار آن یک خط راست خواهد بود.
فرم عمومی یک معادله خطی بهصورت زیر است:
$$ \large a x + b = 0 $$
معادله خطی با یک متغیر، معادله‌ای است که فقط یک متغیر دارد. برای مثال، معادله زیر یک معادله خطی با یک متغیر است که فقط دارای متغیر $$ x $$ است:
$$ \large 12 x - 10 = 0 $$
معادله خطی با دو متغیر یک نوع معادله خطی است دو متغیر دارد و بهصورت زیر نوشته می‌شود:
$$ \large 12 x + 10 y -10= 0 $$
معادله خطی با سه متغیر یک ترکب خطی از سه متغیر است که نمونه‌ای از آن بهصورت زیر است:
$$ \large 12x +23y – 12z = 20 $$
برای آشنایی بیشتر با این نوع معادله، به آموزش «حل معادله درجه اول + فرمول، مثال و حل مسئله» مراجعه کنید.
معادله درجه دو
معادله درجه دوم یا معادله مربعی (Quadratic Equation) معادله‌ای چندجملهای است که یک متغیر مجهول با توان 2 به‌عنوان بزرگ‌ترین جمله توان‌دار دارد. شکل کلی یک معادله درجه دوم بهصورت زیر است:
$$ \large a x ^ 2 + b x + c = 0 $$
که در آن، $$ a \neq 0 $$.
برای آشنایی بیشتر با معادله درجه دوم، به آموزش‌های «حل معادله درجه دو — به زبان ساده + فیلم آموزش رایگان» و «فرمول دلتا و روش دلتا برای حل معادله درجه ۲ — به زبان ساده» مراجعه کنید.
معادله درجه سه
به زبان ساده، می‌توان گفت که معادله مکعبی یا معادله درجه ۳ معادله یک چندجملهای است که بزرگ‌ترین توان $$ x $$ آن درجه ۳ است. شکل کلی یک معادله درجه ۳ بهصورت زیر است:
$$ \large a x ^ 3 + b x ^ 2 + c x + d = 0 $$
برای آشنایی با حل معادله درجه ۳، پیشنهاد می‌کنیم به مطلب «حل معادله درجه ۳ — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
معادله مثلثاتی
معادله مثلثاتی هر معادله‌ای است که دارای تابع مثلثاتی باشد. حل یک معادله مثلثاتی ممکن است بدون استفاده از ماشین‌حساب انجام شود، در حالی که سایر معادله‌های مثلثاتی ممکن است بسیار پیچیده باشند و برای حل آن‌ها به استفاده از ماشین‌حساب یا محاسبات کامپیوتری نیاز باشد.
برای مثال، معادله زیر یک معادله مثلثاتی است:
$$ \large \sin^2 x + \cos 2x = 0 $$
برای آشنایی بیشتر با معادلات مثلثاتی، به آموزش «معادلات مثلثاتی — به زبان ساده» مراجعه کنید. دقت کنید که برای حل معادلات مثلثاتی، باید به‌خوبی با نسبت‌های مثلثاتی و اتحادهای مثلثاتی آشنایی داشته باشید.
معادله رادیکالی
معادله رادیکالی معادله‌ای است که در آن $$x $$ یا عباراتی شامل $$ x $$ در زیر رادیکال باشد. برای مثال، معادله زیر یک معادله رادیکالی است:
$$ \large \sqrt {a x + b } = c $$
دقت کنید که یک فرم عمومی برای معادله رادیکالی نمی‌توان بیان کرد و آنچه در بالا بیان کردیم، تنها یکی از چندین و چند فرم عمومی معادله رادیکالی است.
برای آشنایی بیشتر با معادله رادیکالی، به آموزش «معادله رادیکالی — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مراجعه کنید.
معادله نمایی
برخی از انواع معادله ها وجود دارند که بهصورت نمایی هستند و نمای آن‌ها به‌جای آنکه یک عدد باشد، یک متغیر مجهول است. یکی از شکل‌های معادله نمایی را می‌توان بهصورت کلی زیر نوشت:
$$ \large a b ^ x = c $$
برای آشنایی با حل معادله نمایی، می‌توانید به آموزش «حل معادله نمایی — به زبان ساده» مراجعه کنید.
مثال‌های انواع معادله ها
در این بخش، مثال‌هایی از انواع معادله‌ها را حل می‌کنیم.
مثال اول انواع معادله ها
معادله درجه اول زیر را حل کنید.
$$ \large x + 5 = 19 $$
حل: عدد $$5$$ را به سمت راست می‌بریم و علامت آن را تغییر می‌دهیم. در نتیجه، جواب بهصورت زیر درخواهد آمد:
$$ \large \begin {aligned} x + 5 & = 19 \\ x & = 19 - 5 \\ & = 14 \end {aligned} $$
مثال دوم انواع معادله ها
معادله درجه دوم زیر را حل کنید.
$$ \large 3 x ^ 2 - 2 x + 3 = 0 $$
حل: می‌دانیم که جواب معادله درجه دوم $$a x ^ 2 + b x + c = 0 $$ از فرمول زیر به‌دست می‌آید:
$$x = \frac { – b \pm \sqrt { b ^ 2 – 4 a c } } { 2 a }$$
با توجه به معادله بالا، $$ a = 3 $$، $$ b = - 2 $$ و $$ c = - 3 $$ است. با استفاده از فرمولی نیز که ارائه کردیم، مقدار $$x$$ بهصورت زیر محاسبه می‌شود:
$$ \large x = \frac { -2 \pm \sqrt { 4 - 4 ( 3 ) ( 3 ) } } { 2 ( 3 ) } = \frac { -2 \pm \sqrt { 40 } } { 6 } = \frac { - 1 } { 3 } \pm \frac { \sqrt { 1 0 } } { 3 } . $$
مثال سوم انواع معادله ها
جواب‌های معادله مثلثاتی زیر را در بازه $$[0 , 2 \pi ] $$ به‌دست آورید:
$$ \large \sin \left ( x - \frac { \pi } { 3 } \right ) = - \frac { 1 } { 2 } $$
حل: از آنجا که $$ - \frac { \pi } { 3 } \leq x - \frac { \pi } { 3 } \leq \frac { 5 } { 3 } \pi $$، خواهیم داشت:
$$ \large \begin {aligned} x - \frac { \pi }{ 3 } & = - \frac { \pi }{ 6 } , \frac { 7 } { 6 } \pi \\\\ \Rightarrow x & = \frac { \pi } { 6 } , \frac { 3} { 2 } \pi \end {aligned} $$
مثال چهارم انواع معادله ها
جواب‌های معادله مثلثاتی زیر را در بازه $$ 0 \leq x \leq 2 \pi $$ به‌دست آورید.
$$ \large 2 \cos ^ 2 x - \sin x - 1 = 0 $$
حل: از آنجا که $$ \sin ^ 2 + \cos ^ 2 = 1 $$، معادله را به‌فرم زیر بازنویسی می‌کنیم و خواهیم داشت:
$$ \large \begin {aligned} 2 \cos ^ 2 x - \sin x - 1 & = 0 \\ \Rightarrow 2 ( 1 - \sin ^ 2 x ) - \sin x - 1 & = 0 \\ \left ( 2 \sin x - 1 \right ) ( \sin x + 1 ) & = 0 \\ \sin x & = \frac { 1 } { 2 } , - 1 . \end {aligned} $$
از آنجا که $$ 0 \leq x \leq 2\pi $$، برای $$ \sin x = \frac { 1 } { 2 } $$ داریم:
$$ \large x = \frac { \pi } { 6 } , \frac { 5 } { 6 } \pi $$
برای $$ x = - 1 $$، داریم:
$$ \large x = \frac { 3 } { 2 } \pi $$
با ترکیب دو جواب اخیر، خواهیم داشت:
$$ \large x = \frac { \pi } { 6 } , \frac { 5 } { 6 } \pi , \frac { 3 } { 2 } \pi $$
مثال پنجم انواع معادله ها
فرض کنید یکی از ریشه‌های معادله زیر، برابر با $$ \alpha $$ باشد. مقدار $$ \sin \alpha \cos 2 \alpha $$ را به‌دست آورید.
حل: دو طرف را به توان ۲ می‌رسانیم:
$$ \large \begin {aligned} ( 1 - 6 \sin x ) ^ 2 & = \left ( \sqrt { 5 - 1 2 \sin x } \right ) ^ 2 \\ 1 - 1 2 \sin x + 3 6 \sin ^ 2 x & = 5 - 1 2 \sin x \\ \sin ^ 2 x & = \frac { 1 } { 9 } \\ \Rightarrow \sin x & = \pm \frac { 1 } { 3 } . \end {aligned} $$
از آنجا که $$ x = - \frac 13 $$ در معادله $$ 1 - 6 \sin x = \sqrt { 5 - 12 \sin x } $$ صدق می‌کند، داریم: $$ \alpha = - \frac 13 $$.
بنابراین، $$ \sin \alpha \cos 2 \alpha $$ برابر خواهد بود با:
$$ \large \begin {aligned} \sin \alpha \cos 2 \alpha & = \sin \alpha \left ( 1 - 2 \sin ^ 2 \alpha \right ) \\ & = - \frac { 1 } { 3 } \left ( 1 - \frac { 2 } { 9 } \right ) \\ & = - \frac { 7 } { 2 7 } \end {aligned} $$
مثال ششم انواع معادله ها
معادله $$ 4 ^ { 3 x } = 8 ^ { x - 1 } $$ را حل کنید.
حل: می‌بینیم که دو پایه متفاوت $$ 4 $$ و $$ 8 $$ داریم. هر دوی این پایه‌ها را می‌توان به $$ 2 $$ تبدیل کرد. با این کار، خواهیم داشت:
$$\large \begin {aligned} 4 ^ { 3 x } & = 8 ^ { x – 1 } \\ \big ( 2 ^ 2 \big ) ^ { 3 x } & = \big ( 2 ^ 3 \big ) ^ { x – 1 } \\ 2 ^ { 6 x } & = 2 ^ { 3 x – 3 } \\ 6 x & = 3 x – 3 \\ x & = – 1 . \ \end {aligned}
$$
مثال هفتم انواع معادله ها
معادله نمایی $$ 5{{\bf{e}}^{2z + 4}} - 8 = 0 $$ را حل کنید.
حل: ابتدا معادله نمایی را به صورت زیر می‌نویسیم:
$$ \large {{\bf{e}}^{2z + 4}} = \frac{8}{5} $$
با توجه به وجود $$ \bf {e}$$ به عنوان پایه نمایی، از دو طرف لگاریتم طبیعی می‌گیریم و خواهیم داشت:
$$ \large \begin {align*} \ln { { \bf { e } } ^ { 2 z + 4 } } & = \ln \left ( { \frac {8 } { 5 } } \right ) \\ 2 z + 4 & = \ln \left ( { \frac { 8 } { 5 } } \right ) \\ 2 z & = \ln \left ( { \frac { 8 }{ 5 } } \right ) - 4 \\ z & = \frac { 1 } { 2 } \left ( { \ln \left ( { \frac { 8 } { 5 } } \right ) - 4 } \right ) = \frac { 1 } { 2 } \left ( { 0.470003629 - 4 } \right ) = - 1.76499819 \end {align*} $$
مثال هشتم انواع معادله ها
معادله رادیکالی زیر را حل کنید.
$$ \large
\sqrt[3]{2 x+3}+5=2
$$
حل: ابتدا معادله را به‌فرم زیر می‌نویسیم:
$$ \large\sqrt[3]{2 x+3}=-3 $$
از آنجا که رادیکال‌ها با فرجه فرد می‌توانند پاسخ‌های منفی داشته باشند، این مسئله جواب دارد. دو طرف معادله را به توان فرجه، یعنی ۳، می‌رسانیم و جواب را به‌دست می‌آوریم:
$$ \large
\begin{aligned}
(\sqrt[3]{2 x+3})^{3} &=(-3)^{3} \\
2 x+3 &=-27 \\
2 x &=-30 \\
x &=-15
\end{aligned}
$$
معرفی فیلم آموزش ریاضی پایه هفتم
برای آشنایی بیشتر با مباحث درس ریاضی پایه هفتم، پیشنهاد می‌کنیم فیلم آموزش ریاضی پایه هفتم فرادرس را مشاهده کنید که در ۱۳ ساعت و ۳ دقیقه تدوین شده و همه مباحث 14 درس کتاب درسی را به‌طور کامل پوشش می‌دهد. در فصل یکم این آموزش، راهبردهای حل مسئله معرفی می‌شود. فصل دوم درباره عددهای صحیح است. فصل سوم درباره جبر و معادله است. در فصل چهارم به هندسه و استدلال پرداخته شده است. موضوع فصل ششم سطح و حجم است. در فصل هفتم به توان و جذر پرداخته شده است. فصل هشتم به بردار و مختصات اختصاص یافته است و در نهایت، آمار و احتمال در فصل نهم معرفی می‌شود.
- برای مشاهده فیلم آموزش ریاضی پایه هفتم + اینجا کلیک کنید.
جمع‌بندی
در این آموزش، با انواع معادله های ریاضی از قبیل معادله درجه ۱، معادله درجه ۲، معادله درجه ۳، معادله مثلثاتی، معادله رادیکالی، معادله نمایی و... آشنا شدیم و مثال‌های متنوعی از آن‌ها را حل کردیم.
