اعداد کاتالان — به زبان ساده

«اعداد کاتالان» (Catalan Numbers) دنباله‌ای از اعداد صحیح مثبت هستند که در بسیاری از مسائل شمارش مبحث ترکیب ظاهر می‌شوند. این اعداد انواع خاصی از مسیرهای مشبک، درخت‌های باینری و بسیاری از اشیاء ترکیبی دیگر را شمارش می‌کنند. اعداد کاتالان در یک رابطه بازگشتی پایه صدق می‌کنند و یک فرمول بسته برحسب ضرایب دوجمله‌ای دارند.

تعریف اعداد کاتالان

اعداد کاتالان $$ C _ 0$$، $$ C_ 1 $$، ... ، $$ C_ n $$ و... از فرمول زیر به دست می‌آیند:

$$ \large C _ n = \frac { 1 } { n + 1 } \dbinom { 2 n } { n } . $$

فیلم آموزش ریاضی – پایه دهم | رشته های تجربی و ریاضی در فرادرس

کلیک کنید

چند عدد نخست از اعداد کاتالان به صورت زیر هستند:

$$ \large \begin {aligned} C _ 0 & = 1 \\ C _ 1 & = 1 \\ C _ 2 & = 2 \\ C _ 3 & = 5 \\ C _ 4 & = 1 4 \\ C _ 5 & = 4 2 . \end {aligned} $$

از این تعریف نمی‌توان بلافاصله فهمید که $$ C _ n $$ها اعدادی صحیح هستند، اما این امر از بسیاری از قضایای اثبات شده زیر پیروی خواهد کرد.

مسیرهای دایک و دنباله‌های پذیرفتنی

قضیه: تعداد عبارات پرانتز مجاز که شامل $$ n $$ پرانتز راست و $$ n $$ پرانتز چپ است، برابر با $$ n $$اُمین عدد کاتالان است. برای مثال، $$ C _ 3 = 5 $$ بوده و ۵ راه برای ایجاد عبارات معتبر با ۳ مجموعه از پرانتز‌ها وجود دارد:

• ( ) ( ) ( )
• ( ( ) ) ( )
• ( ) ( ( ) )
• ( ( ( ) ) )
• ( ( ) ( ) )

با در نظر گرفتن پرانتزهای سمت راست به عنوان $$ + 1 $$ و پرانتزهای سمت چپ به عنون $$ - 1 $$، می‌توانیم این‌گونه بنویسیم: اعداد دنباله $$ a _ 1 $$، $$ a _ 2 $$، ... و $$ a _{ 2 n } $$ متشکل از $$ 2 n $$ جمله را که می‌توان با استفاده از $$ n $$ نسخه از $$ + 1 $$ها و $$ n $$ نسخه از $$ - 1 $$ها تشکیل داد، آن‌هایی هستند که در مجموع جزئی زیر صدق می‌کنند:

$$ \large a _ 1 + a _ 2 + \cdots + a _ k \ge 0 $$

که در آن، $$ k = 1 , 2 , 3 , \ldots , 2 n $$ برابر است با $$n$$اُمین عدد کاتالان است.

اثبات: دنباله‌ای از $$ n $$ نسخه از $$ + 1 $$ها و $$ n $$ نسخه از $$ - 1 $$ها را «پذیرفتنی» (Acceptable) گوییم اگر در شرط بالا صدق کند،‌ در غیر این صورت «نپذیرفتنی» (Unacceptable) است. تعداد دنباله‌های پذیرفتنی را با $$ A_ n $$ و تعداد دنباله‌های نپذیرفتنی را با $$U_ n $$ مشخص می‌کنیم.

تعداد کل دنباله‌های $$ + 1 $$ و $$ - 1 $$ را می‌توان به عنوان جابه‌جایی اشیایی از دو نوع مختلف با $$ n $$ شیء از یک نوع و $$ n $$ تا از نوع دیگر در نظر گرفت. بنابراین، تعداد کل چنین دنباله‌هایی برابر است با:

$$ \large \dbinom { 2 n } { n } = \frac { 2 n ! } { n ! n ! } . $$

در نتیجه، $$ A _ n = \dbinom { 2 n } { n } - U _ n $$ و گام بعدی شمارش $$ U_ n $$ است.

یک دنباله نپذیرفتنی از $$ n $$ نسخه از $$ + 1 $$ها و $$ n $$ نسخه از $$ -1 $$ها را در نظر بگیرید. کوچک‌ترین عدد $$ k $$ به گونه‌ای وجود دارد که مجموع جزئی $$ a _ 1 + a _ 2 + \cdots + a _ k $$ منفی باشد. با توجه به کمینگی $$ k $$، باید تعدادِ برابرِ $$ + 1 $$ و $$ - 1 $$ قبل از $$ a _ k $$ وجود داشته باشد. بنابراین باید $$ k $$ فرد بوده و رابطه $$ a _ 1 + a _ 2 + \cdots + a _ { k - 1 } = 0 $$ و $$ a _ k = -1 $$ را داشته باشیم. در نتیجه، از بین جملات $$ ( a _ 1 , a _ 2 , . . . , a _ k ) $$ تعداد $$ \frac { k - 1 } { 2 } $$ نسخه از $$ + 1 $$ و $$ \frac { k - 1 } { 2 } + 1 = \frac { k + 1 } { 2 } $$ نسخه از $$ - 1$$ وجود دارد. از بین جملات باقیمانده $$ a _ { k + 1 }$$، ... و $$ a _ { 2 n } $$، تعداد $$ \big ( n - \frac { k - 1 } { 2 } \big ) $$ نسخه از $$ + 1 $$ و $$ \big ( n - \frac { k + 1 } { 2 } \big ) $$ نسخه از $$ - 1 $$ وجود دارد.

حال، اثر معکوس کردن علامت هر یک از $$ k $$ جمله اول، یعنی جایگزینی $$ a _ i $$ با $$ a _ { - i } $$ را برای $$ i = 1 , 2 , ... , k $$ در نظر بگیرید. سایر جملات را تغییر نمی‌دهیم. اکنون این دنباله جدید به دست آمده و آن را $$ b _ 1 $$، $$ b _ 2 $$، $$ b _ 2 $$، $$ b _ 3 $$، ... و $$ b _ { 2 n } $$ می‌نامیم که $$ n + 1 $$ نسخه از $$ + 1 $$ها و $$ n - 1 $$ نسخه از $$ - 1$$ها دارد (زیرا به ۲ اضافه می‌شوند).

این موضوع، تابع $$ f $$ را از مجموعه دنباله‌های نپذیرفتنی تا مجموعه دنباله‌هایی از $$ \pm 1 $$ را که با ۲ جمع می‌شوند نتیجه می‌دهد. برای مشاهده یک به یک بودن تابع $$ f $$، معکوس آن را تشکیل می‌دهیم: فرض کنید $$ B = b _ 1 , b _ 2 , \ldots , b _ { 2 n } $$ دنباله‌ای از جملات $$ \pm 1 $$ها باشد که با 2 جمع می‌شوند. فرض کنید $$ k $$ اولین اندیس برای حالتی باشد که در $$ b _ 1 , b _ 2 , \ldots , b _ k $$ تعداد $$ +1 $$ بیشتری نسبت به $$ - 1 $$ها وجود داشته باشد (باید چنین $$k$$ای وجود داشته باشد، زیرا مجموع همه جملات مثبت است). بنابراین $$ g ( B ) $$ را تعریف می‌کنیم که باید دنباله (نپذیرفتنی) $$ - b _ 1 , - b _ 2 , \ldots , - b _ k , b _ { k + 1 } , b _ { k + 2 } , \ldots , b _ { 2 n } $$ باشد. واضح است که $$ f $$ و $$ g $$ معکوس هم هستند.

اکنون تعداد دنباله‌های $$ n + 1 $$ نسخه از $$+1$$ها و $$ n - 1 $$ نسخه از $$ - 1 $$ها برابر با $$ \frac { 2 n ! } { ( n + 1 ) ! ( n - 1 ) ! } $$ است. با توجه به یک به یک بودن، همچنین، این تعداد برابر با تعداد دنباله‌های نپذیرفتنی نیز هست. بنابراین، تعداد کل دنباله‌های نپذیرفتنی به صورت زیر است:

$$ \large U _ n = \frac { 2 n ! } { ( n + 1 ) ! ( n - 1 ) ! } . $$

در نتیجه، تعداد دنباله‌های پذیرفتنی برابر است با:

$$ \large \begin {aligned} A _ n & = \frac { ( 2 n ) ! } { n ! n ! } - U _ n \\ & = \frac { ( 2 n ) ! } { n ! n ! } - \frac { ( 2 n ) ! } { ( n + 1 ) ! ( n - 1 ) ! } \\ & = \frac { ( 2 n ) ! } { n ! ( n - 1 ) ! } \left ( \frac 1 { n } - \frac 1 { n + 1 } \right ) \\ & = \frac { ( 2 n ) ! } { n ! ( n - 1 ) ! } \frac1 { n ( n + 1 ) } \\ & = \frac 1 { n + 1 } \frac { ( 2 n ) ! } { n ! n ! } \\\\ & = C _ n . \end {aligned} $$

و اثبات کامل می‌شود.

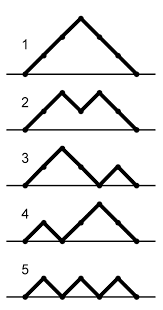
نکته ۱: این دنباله‌ها همچنین «مسیرهای دایک» (Dyck Paths) به طول $$ 2 n $$ را توصیف می‌کنند که دنباله‌هایی از فواصل مساوی شمال شرقی و جنوب شرقی را می‌پیمایند که از مبداء آغاز شده و به محور $$ x $$ ختم می‌شوند و هرگز زیر محور $$ x $$ نمی‌روند. یک به یک بودن بين دنباله‌های پذیرفتنی و مسیرهای دایک، یک $$ + 1 $$ را به حرکت شمال شرقی و یک $$ - 1 $$ به یک حرکت جنوب شرقی اختصاص می‌دهد. شرايط پذيرش، معادل مسیری است كه هرگز زير خط شروع و پايان نمی‌رود.

نکته ۲: طبق آنچه گفتیم، می‌توان دریافت که اعداد کاتالان اعدادی صحیح هستند، اگرچه این موضوع از اتحاد $$ C _ n = \binom { 2 n } { n } - \binom { 2 n } { n + 1 } $$ نیز به دست می‌آید که از اثبات بالا آورده شده است.

رابطه بازگشتی و تابع مولد

یک ابزار مفید برای اثبات‌های مرتبط با اعداد کاتالان، رابطه بازگشتی توصیف کننده آن‌ها است.

فیلم آموزش آمار و احتمال – پایه یازدهم در فرادرس

کلیک کنید

قضیه: اعداد کاتالان در رابطه بازگشتی زیر صدق می‌کنند:

$$ \large C _ { n + 1 } = C _ 0 C _ n + C _ 1 C _ { n - 1 } + \cdots + C _ n C _ 0 = \sum _ { k = 0 } ^ n C _ k C _ { n - k } . $$

اثبات: چند راه برای اثبات این قضیه وجود دارد، اما شاید زیرکانه‌ترینشان با مسیرهای دایک به طول $$ 2 ( n + 1 ) $$ باشد که در بالا $$ C _ { n + 1 } $$ شمارش را دیدیم. برای یک مسیر دایک به طول $$ 2 ( n + 1 ) $$، فرض می‌کنیم $$ 2 ( k + 1 ) $$ اولین مختصات $$ x $$ غیرصفر نخست باشد که در آن، مسیر به محور $$ x $$ برخورد می‌کند و $$ 0\le k \le n $$.

مسیر به دو بخش می‌شکند، بخش چپ $$ 2 ( k + 1 ) $$ و بخش سمت راست آن. بخش راست یک مسیر دایک به طول $$ 2 ( n - k ) $$ است، بنابراین، با $$ C _ { n - k } $$ شمارش می‌شود. بخش چپ یک گام در جهت شمال شرقی است، سپس یک مسیر دایک به طول $$ 2 k $$ و آنگاه یک گام جنوب غربی طی می‌شود (مسیر میانی یک مسیر دایک است که هرگز به زیر نقطه شروع خود نمی‌رود، زیرا نمی‌تواند پیش از $$ 2 ( k + 1 ) $$ به محور $$ x $$ برخورد کند). تعداد $$ C_ k $$ تا از این‌ها وجود دارد. بنابراین، در کل $$ C_ k C _ {n - k } $$ مسیر وجود دارد که ابتدا در $$ 2 ( k + 1 ) $$ به محور $$ x $$ برخورد می‌کنند و مجموع این جملات به $$ C _ { n + 1 } $$ می‌رسد که یک رابطه بازگشتی است.

مثال: اگر $$ n + 1 = 3 $$ باشد، آنگاه $$ C _ { n + 1 } $$ پنج مسیر دایک شکل بالا را می‌شمارد:

• مسیر 1 دارای $$ k = 2 $$ است، و در $$ C _ 2 C_ 0 $$ شمارش شده است.
• مسیر ۲ دارای $$ k = 2 $$ است، و در $$ C _ 2 C_ 0 $$ شمارش شده است.
• مسیر ۳ دارای $$ k = 1 $$ است، و در $$ C _ 1 C_ 1 $$ شمارش شده است.
• مسیر ۴ دارای $$ k = 0 $$ است، و در $$ C _ 0 C_ 2 $$ شمارش شده است.
• مسیر ۵ دارای $$ k = 0 $$ است، و در $$ C _ 0 C_ 2 $$ شمارش شده است.

مسیر میانی به طول ۴ در مسیرهای ۱ و ۲، و نیمه پایینی قله چپ مسیر ۳، مسیرهای دایک در اثبات بالا هستند.

رابطه بازگشتی رابطه مفیدی است، زیرا می‌توان از آن برای اثبات این موضوع استفاده کرد که دنباله‌ای از اعداد، دنباله اعداد کاتالان است. اگر دنباله (آن را $$ S_ n $$ می‌نامیم) در رابطه بازگشتی مشابهی با اعداد کاتالان صدق کند و شرایط اولیه مشابه $$ S_ 0 = 1 $$ را داشته باشیم، آنگاه طبق استقرا تساوی $$ S_ n = C_ n $$ را داریم.

قضیه: تابع مولد اعداد کاتالان به صورت زیر است:

$$ \large \sum _ { n = 0 } ^ \infty C _ n x ^ n = \frac { 1 -\sqrt { 1 - 4 x } } { 2 x } = \frac 2 { 1 + \sqrt { 1 - 4 x } } . $$

اثبات: تابع $$ f ( x ) = \sum \limits _ { n = 0 } ^ \infty C _ n x ^ n $$ را در نظر بگیرید. در نتیجه، می‌توان نوشت:

$$ \large \begin {aligned} x f ( x ) ^ 2 & = \sum _ { n = 0 } ^ \infty ( C _ 0 C _ n + C _ 1 C _ { n - 1 } + \cdots + C _ n C _ 0 ) x ^ { n + 1 } \\ & = \sum _ { n = 0 } ^ \infty C _ { n + 1 } x ^ { n + 1 } \\ & = f ( x ) - 1 . \end {aligned} $$

بنابراین، طبق فرمول، ریشه‌های $$ f ( x ) = \frac { 1 \pm \sqrt { 1 - 4 x } } { 2 x } $$ را خواهیم داشت، اما علامت منفی تنها انتخاب است که معنی دارد، زیرا علامت مثبت منجر به عبارتی می‌شود که در $$ x = 0 $$ تعریف نشده است (انتخاب علامت منفی به عبارتی می‌انجامد که یک حد $$ x \to 0 $$ دارد و طبق قاعده هوپیتال، داریم: $$ \lim _ { x \to 0 } \frac { 1 - \sqrt { 1 - 4 x } } { 2 x } = \lim _ { x \to 0 } \frac { 2 ( 1 - 4 x ) ^ { - 1 / 2 } } 2 = 1 $$.

سایر کاربردهای اعداد کاتالان

مثال: شخصی $$ n $$ بلوک به شمال و $$ n $$ بلوک به غرب از محل اقامتش حرکت می‌کند.

فیلم آموزش کاربردی برنامه نویسی سی شارپ در فرادرس

کلیک کنید

او هر روز $$ 2 n $$ بلوک برای حرکت دارد. اگر او هیچگاه از خط قطری خانه به دفتر کار عبور نکند، چه تعداد مسیر ممکن موجود دارد؟‌

پاسخ: واضح است که هر مسیر پذیرفتنی در بالا یا پایین خط قطری بوده و هر دوی این مسیرها متقارن هستند. بنابراین، تعداد مسیرهای زیر قطر را در ۲ ضرب می‌کنیم. هر مسیر دنباله‌ای از $$ n $$ بلوک شمالی و $$ n $$ بلوک غربی است. غرب را با $$ + 1 $$ و شمال را با $$ - 1 $$ مشخص می‌کنیم. هر مسیر متناظر با دنباله $$ a _ 1 $$، $$ a _ 2 $$، ... و $$ a _ { 2 n } $$ از $$ n $$ نسخه از $$ + 1 $$ها و $$ n $$ نسخه از $$ - 1 $$ها است. اما برای آنکه مسیر بالاتر از قطر نرود، باید برای $$ k = 1 , 2 , \ldots , 2 n $$، داشته باشیم:

$$ \large a _ 1 + a _ 2 + \cdots + a _ k \ge 0 $$

بنابراین، تعداد مسیرهای پذیرفتنی بالای قطر برابر با $$ n $$اُمین عدد کاتالان است و کل تعداد مسیرهای پذیرفتنی برابر است با:

$$ \large C _ n = \frac { 2 } { ( n + 1 ) } \times \frac { ( 2 n ) ! } { n ! n ! } . $$

نمودار بالا مسیرهای زیر قطر را برای $$ n = 5 $$ نشان می‌دهد. توجه کنید که تعداد چنین مسیرهایی برابر با $$ C_ 5 = 42 $$ است. بنابراین، جواب $$ 2 \times 42 = 84 $$ خواهد بود.

مثال: یک درخت باینری ریشه‌دار درختی است که یک گره ریشه دارد. گره ریشه گره‌ای است دارای صفر یا دو شاخه متصل به گره فرزند است. یک گره درونی یا داخلی است اگر دو گره داشته باشد که دو گره از آن آمده باشند. چه تعداد از درخت‌های باینری ریشه‌دار با $$ n $$ گره داخلی وجود دارند؟

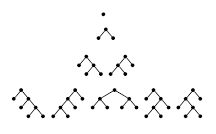
پاسخ: این موضوع یک توضیح خوب از اثبات این موضوع است که یک دنباله با استفاده از رابطه بازگشتی معادل با اعداد کاتالان است. فرض کنید $$ R _ n $$ تعداد درخت‌های ریشه‌دار باینری با $$ n $$ گره داخلی باشد. در نتیجه، $$ r_ 0 = R_ 1 = 1 $$ بوده که مطابق شکل بالا است. اکنون برای $$ n \ge 0 $$، فرض کنید یک درخت باینری ریشه‌دار با $$ n + 1 $$ گره داخلی وجود داشته باشد. گره ریشه داخلی است. تعداد $$ k $$ گره داخلی در چپ و $$ n - k $$ گره داخلی در راست وجود دارد. با نگاهی به سمت چپ و راست دو درخت باینری ریشه‌دار، به ترتیب، $$ k $$ و $$ n - k $$ گره داخلی خواهیم داشت. در نتیجه، می‌توان نوشت:

$$ \large R _ { n + 1 } = \sum _ { k = 0 } ^ n R _ k R _ { n - k } $$

که مشابه رابطه بازگشتی مانند اعداد کاتالان است. بنابراین، برای همه‌ $$ n $$ها، رابطه $$ R_ n = C_n $$ را داریم.

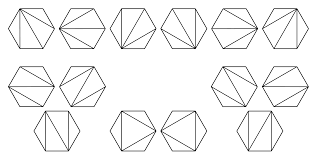
مثال: چند راه برای تقسیم یک $$ n + 2 $$ ضلعی به $$ n $$ مثلث وجود دارد (با رسم $$ n - 1 $$ خط غیرمتقاطع بین رئوس چندضلعی)؟

پاسخ: فرض کنید $$ T_ n $$ تعداد این مثلث‌‌ها باشد و $$ T_ 0 = 1 $$ را تعریف می‌کنیم. $$ T_ {n+1} $$ را چیزی در نظر می‌گیریم که یک $$ ( n + 3 ) $$ ضلعی را می‌شمارد و مثلث‌سازی‌ها را دسته‌بندی می‌کند.

رئوس را $$ v _ 1 $$، $$ v _ 2 $$، ... و $$ v _ { n + 3 } $$ نامگذاری می‌کنیم. فرض کنید یال $$ v _ 1 v _ 2 $$ باشد. اگر مثلث این لبه به پایان برسد، $$ v _ 1 v _ 2 v _ k $$ را خواهیم داشت، آنگاه این مثلث چندضلعی را به دو چندضلعی باقیمانده تقسیم می‌کند که باید مثلث شده باشد.

• اگر $$ k = 3 $$ باشد، آنگاه آنچه در سمت چپ است، یک $$ n + 2 $$ضلعی است. تعداد سه‌گوش‌ها مشابه این $$ T_0 T_ n $$ است.
• اگر $$ k = 4 $$ باشد، یک مثلث $$ v _ 2 v _ 3 v _ 4 $$ روی یک ضلع است و یک $$ ( n + 1 ) $$ ضلعی روی ضلع دیگر است. تعداد سه‌گوش‌ها مانند این $$ T_ 1 T_ { n - 1 } $$ است.
• اگر $$ k = 5 $$ باشد، یک چهارگوش $$ v _ 2 v _ 3 v _ 4 v _ 5 $$ روی یک ضلع است و یک $$n$$ضلعی روی ضلع دیگر است. تعداد سه‌گوش‌های مشابه این، $$ T_ 2 T _ { n - 2 } $$ است.

با ادامه به همین صورت، خواهیم داشت:

$$ \large T _ { n + 1 } = T _ 0 T _ n + T _ 1 T _ { n - 1 } + \cdots + T _ n T _ 0 . $$

همچنین $$ T_ 0 = 1 $$.

این همان رابطه بازگشتی و شرایط اولیه است که اعداد کاتالان را برآورده می‌کند، بنابراین باید برای هر $$ n $$، داشته باشیم: $$ T_ n = C_ n $$.