آنالیز واریانس یک طرفه در SPSS | راهنمای کاربردی
در نوشتارهای دیگر مجله فرادرس با مفهوم تحلیل یا آنالیز واریانس آشنا شدهاید. میدانید که مبنای کار این تکنیک آماری، تجزیه واریانس به چند بخش است که به واسطه آنها، یکسان بودن یا نابرابری چند گروه یا جامعه (به واسطه تفاوت در میانگین) مورد آزمون قرار میگیرد. در این نوشتار با توجه به محبوبیت این تکنیک به بررسی آنالیز واریانس یک طرفه در SPSS پرداختهایم تا به کمک این نرمافزار تحلیلهای مرتبط آنالیز واریانس یک طرفه (One-way ANOVA) را اجرا و نتایج را تفسیر کنیم.

به منظور آشنایی بیشتر با موضوع تحلیل واریانس پیشنهاد میشود، نوشتارهای تحلیل واریانس (Anova) — مفاهیم و کاربردها و استنباط و آزمون فرض آماری — مفاهیم و اصطلاحات را مطالعه کنید. همچنین خواندن مطالب آزمون لون (Levene’s Test) برای برابری واریانس ها در SPSS — راهنمای کاربردی و پس آزمون یا آزمون تعقیبی در تحلیل واریانس | به زبان ساده نیز خالی از لطف نیست.
آنالیز واریانس یک طرفه در SPSS
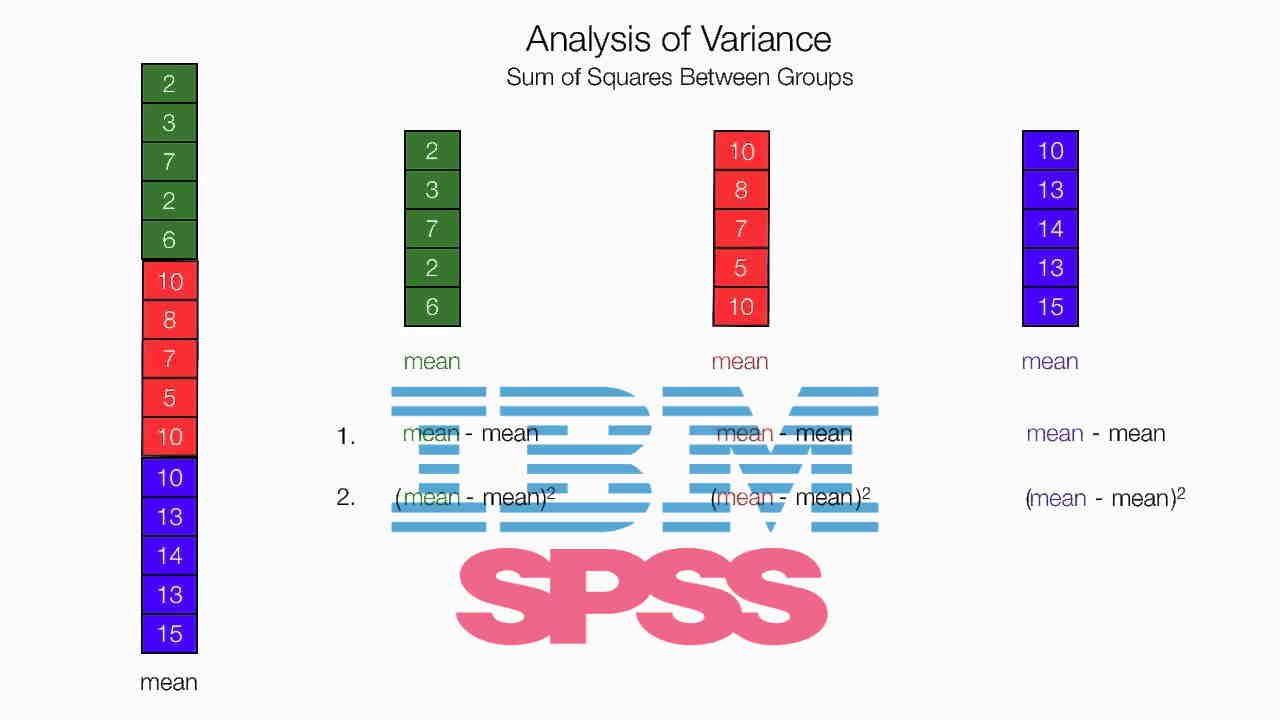
از «آنالیز واریانس یک طرفه» (ANOVA) زمانی استفاده میشود که بخواهیم مشخص کنیم که از نظر آماری تفاوت معنی داری بین میانگین دو یا چند گروه «مستقل» (Unrelated) وجود دارد. اگرچه باید در نظر داشت که بیشتر از ANOVA برای سنجش تفاوت در بیش از سه گروه استفاده میشود. چنین تحلیل را گاهی «آنالیز واریانس تک عاملی» (One-Factor ANOVA) یا «تحلیل واریانس بین آزمودنیها» (Between Subjects ANOVA) مینامند.
به عنوان مثال، شما میتوانید از ANOVA یک طرفه برای درک این واقعیت استفاده کنید که آیا تفاوتی در امتیاز یا رکورد دو سرعت گروههایی که بر اساس سه سطح از میزان مصرف سیگار در بین دانشجویان تشکیل شده است، وجود دارد یا خیر. فرض بر این است که دانشجویان را به سه گروه یا دسته براساس میزان مصرف سیگار، تقسیم بندی کردهایم. این گروهها میتوانند به شکل «غیر سیگاری»، «ترک سیگار» و «مصرف زیاد سیگار« مشخص شده باشند.
مهم است که درک کنیم ANOVA یک طرفه، یک آزمون آماری «کلینگر» (Omnibus) است و نمیتواند به شما بگوید کدام گروه خاص از نظر آماری تفاوت معنی داری با دیگر گروهها دارد. در حقیقت تحلیل واریانس فقط به شما میگوید که حداقل دو گروه متفاوت در بین گروهها مورد بررسی وجود دارد.
از آنجا که ممکن است شما در طرح مطالعاتی، سه، چهار، پنج یا چندین گروه داشته باشید، تعیین اینکه کدام یک از این گروهها با یکدیگر تفاوت دارند، امر مهمی محسوب میشود. شما میتوانید بررسی یا مقایسههای چندتایی (مقایسههای زوجهای همزمان) را به کمک «پس آزمون» (Post Hoc) انجام دهید. این موضوع در انتهای این متن در طرح ANOVA مورد بررسی قرار میگیرد.
نکته: اگر طرح مطالعه شما علاوه بر یک متغیر وابسته و یک متغیر مستقل، یک متغیر سومی نیز دارد که روی متغیر وابسته اثر گذار است، لازم است به جای تحلیل واریانس از «تحلیل کوواریانس» (ANCOVA) استفاده نمایید. برای کسب اطلاعات بیشتر در این زمینه به مطلب ٰتحلیل کوواریانس ANCOVA در SPSS — راهنمای کاربردی مراجعه کنید.

کاربردهای تحلیل واریانس یک طرفه
معمولا در تحلیلهای از نوع «تحلیل میدانی» (Field Studies) و «تحلیل تجربی» (Experiments) و «تحلیل نیمه تجربی» (Quasi Experiments) از آنالیز واریانس یک طرفه یا انواع دیگر تحلیل واریانس استفاده میشود. بر همین اساس به کمک تحلیل یا آنالیز واریانس یک طرفه قادر هستیم آزمونهای زیر را انجام دهیم.
- آزمون تفاوت آماری میانگین یک متغیر پیوسته در بین دو گروه یا بیشتر.
- آزمون تفاوت آماری میانگین یک متغیر پیوسته در دو یا چند بازه زمانی.
- آزمون تفاوت آماری میانگین یک متغیر پیوسته در بین دو یا چند تیمار (Treatments).
در این متن، به شما نشان میدهیم که چگونه یک تحلیل ANOVA یک طرفه را با استفاده از نرمافزار محاسبات آماری SPSS انجام داده و نتایج حاصل از این آزمون را تفسیر و گزارش کنید. از آنجا که ANOVA یک طرفه (One-way) یک آزمون کلینگر است، در صورت رد فرض صفر (رد فرض برابری میانگینها) از پس آزمونها برای مشخص کردن گروه یا گروههای نابرابر استفاده کرده و نتایج را مورد بررسی قرار میدهیم.
نکته: اگر هدف مقایسه دو گروه یا دو نوع تیمار و حتی آزمونهای زوجی به صورت قبل و بعد از تیمار باشد، آزمون T مناسبتر است زیرا محاسبات کمتری داشته و در این حالات، معادل تحلیل واریانس محسوب میشود. اگر آماره آزمون T و آماره آزمون آنالیز واریانس باشد در حالتی که فقط دو جامعه یا دو گروه مقایسه میشوند، رابطه زیر را خواهیم داشت.
قبل از اینکه شما را با نحوه اجرای ANOVA و پسآزمونها آشنا کنیم، فرضیات مختلفی را مرور میکنیم که دادهها باید در تحلیل واریانس دارا باشند. در صورتی که این شرطها برقرار نباشند، نتایج حاصل از ANOVA معتبر نبوده و ممکن است نتایج غلط از خروجیهای نرمافزار SPSS حاصل شود.
آزمون فرض در تحلیل واریانس یک طرفه
همانطور که گفته شد، از تکنیک آنالیز واریانس میتوان برای انجام آزمون فرض آماری برای برابری میانگین چند جامعه استفاده کرد. به این ترتیب فرضیههای این آزمون آماری به صورت زیر در نظر گرفته میشوند.
البته توجه داشته باشید که اگر میانگین گروه یا تیمارهای مختلف باشد، «فرض صفر» (Null Hypotheses) به شکل زیر نوشته میشود.
از طرف دیگر، «فرض مقابل» (Alternative Hypotheses) نیز به صورت زیر بیان میشود.
نکته: رد فرض صفر به معنی نابرابری میانگین همه گروهها نیست. در حقیقت حداقل یکی از میانگینها با بقیه برابر نخواهد بود. به وسیله آزمون کلینگر ANOVA فقط میتوانیم تشخیص دهیم که تساوی برقرار نیست. ولی با پس آزمونها، گروه یا گروههایی که باعث این نابرابری شدهاند را مشخص میکنیم.
شرط یا فرضهای اولیه برای دادهها در تحلیل واریانس
رد یا ضعیف بودن هر یک از فرضیههای زیر برای دادهها، میتواند باعث تضعیف نتایج حاصل از ANOVA بشود. البته بعضی از این شرطها، قبل از انجام آزمون قابل بررسی است ولی بعضی از آنها نیز بعد از اجرای ANOVA باید مورد بررسی قرار گیرند.
فرض شماره ۱
متغیر پاسخ (Dependent Variable) باید از نوع کمی و با مقیاس فاصلهای (Interval Scale) یا نسبتی (Ratio Scale) اندازهگیری شده باشد. به این ترتیب این متغیر به شکل یک متغیر پیوسته در تحلیل ANOVA در نظر گرفته میشود.
فرض شماره ۲
«متغیر مستقل» (Independent Variable) در تحلیل یا آنالیز واریانس، یک متغیر کیفی است که شامل حداقل دو سطح یا دو نوع مقدار است. ممکن است هر یک از این سطوح، بیانگر مقاطع زمانی، نوع تیمار یا نام گروه باشند.
فرض شماره ۳
مشاهدات حاصل از متغیرهای مستقل و وابسته باید نسبت به هم مستقل باشند. به این ترتیب مقادیر این متغیرها در مشاهده اول، ارتباطی با مقادیر مربوط به مشاهده دوم یا هر مشاهده دیگر ندارد. شرط «استقلال» (Independence) مشاهدات را میتوان به کمک به کارگیری «روشهای نمونهگیری» (Sampling Method) مناسب برآورده کرد.
فرض شماره ۴
داده پرت و مقادیر گمشده ممکن است باعث انحراف نتایج حاصل از تحلیل واریانس شوند. بنابراین قبل از شروع عملیات آنالیز واریانس یک طرفه در SPSS لازم است نسبت به برطرف کردن «مقادیر پرت» (Outlier) و «گمشده» (Missing) اقدام کرد.
به کمک تکنیک و روشهای مختلفی در SPSS میتوان «دادههای پرت» (Outlier Data) را شناسایی کرد. البته الگوریتمهای بهینهای نیز مانند «الگوریتم جنگل تصادفی ایزوله» (Isolation Forest Algorithm) برای انجام این کار در مجموعه دادههای بزرگ وجود دارد.
از طرفی شاید لازم باشد سطرها یا مشاهداتی که دارای «مقادیر گمشده» (Missing) هستند، حذف یا مقدار دهی کرد. اگر حجم نمونهها در هر یک از گروهها کم است بهترین روش، مقدار دهی مقادیر گمشده با میانگین مقادیر گروه مورد نظر است.
فرض شماره ۵
متغیر وابسته در تحلیل واریانس یک طرفه (و البته هر نوع تحلیل واریانس دیگر) باید به طور تقریبی دارای توزیع نرمال باشد. در حقیقت توزیع دادههای متغیر کمی در هر سطح از متغیر کیفی (گروه یا تیمارها) باید نرمال باشد. «آزمون نرمال بودن» (Normality Test) برای این دادهها را میتوان به وسیله آزمونهای مختلفی مانند «آزمون شاپیرو ولیک» (Shapiro-Wilk's Normality Test) یا «آزمون کولموگروف اسمیرنف» (Kolmogrov-Smirnov Normality Test) انجام داد.
نکته: نرمال نبودن مشاهدات یا «دم کلفت» (Thick-tailed) بودن یا «چولگی زیاد» (Heavily Skewed) در توزیع، نمیتواند نتایج آنالیز واریانس یک طرفه را خیلی تحت تاثیر قرار دهد. به همین علت اصطلاح تقریبا نرمال را به کار بردهایم.
فرض شماره ۶
تصادفی بودن دادهها در تحلیل واریانس اهمیت زیادی دارد. البته این شرط را پس از انجام آنالیز واریانس و بدست آوردن باقیماندههای مدل نیز میتوان مورد بررسی قرار داد. اگر باقیماندهها، به صورت تصادفی حاصل شوند، میتوان این فرض را نیز در نظر گرفت که مشاهدات متغیر وابسته، به صورت تصادفی توزیع شدهاند.
فرض شماره ۷
«یکسان بودن واریانس» (Homogeneity of variances) در بین هر کدام از گروهها یا تیمارها برای متغیر وابسته نیز یکی از شرطهای مهم در آنالیز واریانس یک طرفه است. توجه داشته باشید که اگر شرط برابری واریانس در بین گروهها رد شود و تعداد مشاهدات در هر دسته نیز در آنالیز واریانس یک طرفه، نابرابر باشند، مقدار آماره نمیتواند گواهی بر رد فرض صفر یا عدم رد آن باشد. در این صورت باید از آماره تعدیل شده دیگری مانند «آماره ولچ» (Welch Statistics) یا «آماره براون-فورسیت» (Brwone-Forsythe) استفاده کرد. همچنین در این وضعیت نیز استفاده از پس آزمونها محدود شده و فقط بعضی از آنها مانند Dunnet C، به کار گرفته میشوند.
نکته: در صورتی که فرضیات مربوط به توزیع نرمال، برابری واریانسها و عدم وجود دادههای پرت برقرار نباشد، باید به جای استفاده از تحلیل واریانس، به سراغ روشهای ناپارامتری مانند «آزمون فریدمن» (Friedman Test) رفت.
البته بعضی از محققین، شرطهای دیگری را هم برای «تحلیل واریانس» (ANOVA) در نظر میگیرند. برای مثال وجود حداقل ۶ آزمودنی در هر یک از گروهها یا استفاده از طرح متعادل (برابری تعداد در هر گروه) را برای کسب نتایج دقیق و صحیح در آنالیز واریانس در نظر میگیرند.
آماره آزمون در تحلیل واریانس
جدول تحلیل واریانس زیر را در نظر بگیرید. آماره آزمون () براساس نسبت میانگین مربعات تیمارها بر میانگین خطاها، بدست میآید.
|
منبع تغییرات Variation Source |
مجموع مربعات Sum of Squares |
درجه آزادی df | میانگین مربعات
Mean Square | آماره F |
| تیمار (Treatments) | SSTr | |||
| خطا (Error) | SSE | |||
| کل (Total) | SST |
اگر گروه یا تیمار وجود داشته باشد، آنگاه درجه آزادی تیمارها یا گروهها برابر با و درجه آزادی عبارت خطا نیز خواهد بود. واضح است که ، تعداد کل مشاهدات را نشان میدهد. در ضمن درجه آزادی تغییرات کل نیز برابر با است.
در ضمن بین مجموع مربعات تیمارها و مجموع مربعات خطا رابطه زیر برقرار است.
نکته: در برخی متون آماری ممکن است نماد یا برای درجه آزادی تیمار و یا برای درجه آزادی خطای در نظر گرفته شود. همچنین گاهی به جای استفاده از SSTr از SSR (بخصوص در زمانی که تحلیل رگرسیون صورت گرفته) در جدول آنالیز واریانس، استفاده میکنند.
اصطلاحات «تیمار» (Treatment) یا مدل و «خطا» (Error) اصطلاحاتی هستند که بیشتر در متون مربوط به مباحت «طراح آزمایشها» (Experimental Design) مورد استفاده قرار میگیرد. ولی در علوم اجتماعی، اغلب دیده میشود که اصطلاحات «بین گروهی» (Between Groups) به جای «تیمار» و «درون گروهی» (Within Groups) به جای «خطا» به کار میروند. عبارت «بین/درون» (Between/Within)، اصطلاحاتی هستند که در نرمافزار SPSS و در خروجی آنالیز واریانس نیز ظاهر میشوند.
نحوه اجرای آنالیز واریانس یک طرفه در SPSS
حال که با نحوه محاسبات و خصوصیات تحلیل واریانس آشنا شدید، باید شیوه اجرای آن را در محیط SPSS یادآوری کنیم. این بخش به نحوه دسترسی به این فرمان و همچنین تنظیمات و گزینههای انتخابی برای اجرای آنالیز واریانس یک طرفه در SPSS میپردازد.
اجرای دستور One-way ANOVA
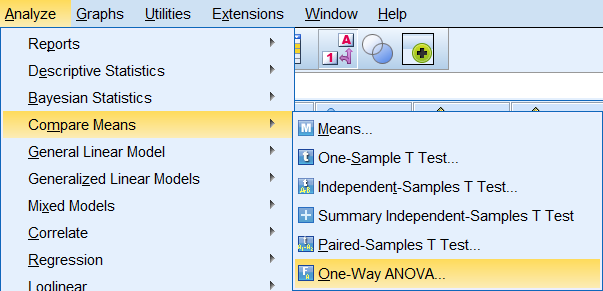
برای تعیین پارامترها و معرفی متغیرهای مورد آزمون در تحلیل واریانس یک طرفه در SPSS، فرمان One-way ANOVA را از فهرست (Menu) تحلیل (Analyze) و بخش Compare Means اجرا میکنیم. به این ترتیب طبق تصویر ۲، مسیر دسترسی مشخص میشود. به شکل نوشتاری نیز مسیر دسترسی به این دستور را به صورت زیر نشان دادهایم.
Analyze > Compare Means > One-Way ANOVA
تعیین پارامترهای تحلیل واریانس یک طرفه
در گام بعدی باید با توجه به متغیرهای مستقل و وابسته، تنظیماتی را در پنجره One-Way ANOVA انجام دهیم. در تصویر ۳، مکان قرارگیری هر یک از متغیرها و گزینههای مشخص شدهاند.
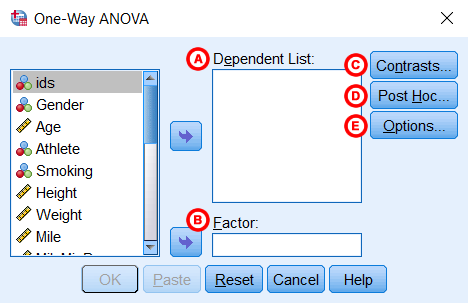
هر یک از بخشهای این پنجره در ادامه معرفی و کاربرد آنها نیز مشخص میشود
لیست متغیرهای وابسته (A): در قسمت (Dependent List)، متغیر یا متغیرهایی که به عنوان «متغیر وابسته» (Dependent Variables) در تحلیل به کار رفتهاند، قرار میگیرد. البته توجه دارید که هر یک از این متغیرها، یک خروجی برای آنالیز واریانس یک طرفه تولید میکند. به این ترتیب میتوان چندین تحلیل واریانس را با یک دستور و البته یک روش تیمار یا گروهبندی، اجرا کرد. به یاد داشته باشید که باید از متغیرهای نوع scale که با علامت خط کش مشخص شدهاند در این کادر، استفاده کنید.
متغیر عامل (B): بخش Factor در این پنجره، مخصوص متغیر مستقل است. این متغیر معمولا از نوع کیفی بوده و با مقیاسهای اسمی (Nominal) به شکل سه دایره رنگی یا ترتیبی (Ordinal) با سه ستون رنگی، در بخش متغیرها (کادر سمت چپ) مشخص میشوند. این متغیر باید دارای حداقل دو سطح یا مقدار متمایز باشد.
نکته: اگر متغیرها را به درستی انتخاب نکرده باشید، نرمافزار SPSS، اشکالی نخواهد گرفت و نتایج را نمایش میدهد. ولی ممکن است این نتایج نامرتبط یا نامشخص نسبت به تحلیل مورد نظرتان باشند.
تضادها (C): بخش بعدی یا (Contrast) مربوط به «پیشآزمونها» (Prio Test) است که به صورت تحلیلها یا «مقایسههای طرحریزی شده» (Planned Comparison) به کار میرود. تضاد «چند جملهای» (Polynomial) و مشخص کردن ضریب هر یک از سطوح متغیر عامل در تعیین این تضادها لازم است. اغلب باید مجموع ضرایب تعیین شده برای این تضادها، صفر باشد. در انتهای پنجره One-Way ANOVA: Contrasts این جمعبندی صورت گرفته است و میتوان صفر بودن را مورد بررسی قرار داد. با انتخاب این گزینه، پنجرهای به مانند تصویر ۴ ظاهر خواهد شد.
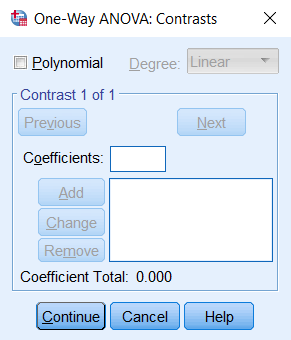
این تضادها میتواند به صورت «مقایسههای دو تایی» یا «چندتایی» (Multiple Comparison) به صورت دلخواه تعیین شده و تحلیل واریانس را مطابق با درخواست شما در سطوح مختلف متغیر عامل اجرا کنند.
پس آزمونها (D): اگر طبق تحلیل یا آنالیز واریانس یک طرفه، فرض صفر رد شود، لازم است بدانیم که کدام گروه یا گروهها باعث ایجاد نابرابری شدهاند. در این بخش به کمک روشهای مختلف معرفی شده برای انجام «پس آزمونها» (Post-Hoc) محاسبات را دنبال میکنیم. البته شرط برابری واریانس یا نابرابری آن در انتخاب پس آزمون نقش مهمی دارد. در تصویر ۵ پنجره پس آزمونهای مربوط به آنالیز واریانس یک طرفه در SPSS دیده میشود.

بخشهای مختلف این پنجره نیز در ادامه مورد بررسی قرار میگیرند. البته به یاد داشته باشید که در صورت رد فرض صفر به خروجی Post-Hoc توجه خواهیم کرد و اگر دلیلی بر رد فرض صفر وجود نداشته باشد، باید بخش خروجی پس آزمون را نادیده گرفت.
- با فرض برابری واریانسها، گزینههای بخش Equal Variances Assumed مربوط به روشهای مختلف پس آزمون است که در بین گروه یا تیمارهای مختلف، قابل اجرا است.
- آزمون Dunnet که به بررسی گروه کنترل با دیگر سطوح متغیر عامل میپردازد، میتواند به شکل آزمون فرض دو طرفه یا sided - ٬2 یا یک طرفه (< Control یا > Control) باشد. البته تعیین گروه کنترل نیز در این بخش قابل انجام است.
- اگر فرض برابری واریانسها در بین گروهها رد شده باشد، گزینههای بخش Equal Variances Not Assumed، روشی مناسب برای انجام آزمونهای مقایسهای و پس آزمونها یا آزمونهای تعقیبی هستند.
- سطح معنیداری یا میزان خطای نوع اول برای پس آزمونها نیز در این بخش تعیین میشود.
نکته: هنگامی که آماره F نشان میدهد که تفاوت معنی داری بین میانگین گروهها وجود دارد، آزمون تعقیبی یا پس آزمونها برای تعیین اینکه کدام گروه خاص باعث رد فرض صفر شده، به کار میآید. آزمونهای تعقیبی هر جفت از گروهها را (مثلا براساس آزمون t نمونههای مستقل) مقایسه کرده اما برخلاف آزمونهای t، میزان خطای نوع اول را برای چندین آزمون همزمان، تصحیح میکنند تا برای مقایسههای چندگانه مشکل تورم خطا در برآوردگر واریانس رخ ندهد.
تنظیمات اختیاری (E): با انتخاب گزینه Options در پنجره پارامترهای One-Way ANOVA، امکاناتی برای محاسبه یا آزمون در مورد شاخصهای آماری، نظیر «آزمون برابری واریانس در بین گروهها» (Homogenity of variance test) قابل اجرا است. همچنین در صورت رد فرض برابری واریانسها، آماره (Brown-Forsythe) و (Welch) به جای آماره F، قابل استفاده است. ترسیم نمودار Means plot هم به درک و نمایش اختلاف بین میانگینها کمک شایانی میکند و به کمک آن میتوان روند تغییرات میانگین را در بین گروهها تشخیص داد. گزینههای مختلف این پنجره در تصویر ۶ دیده میشود.
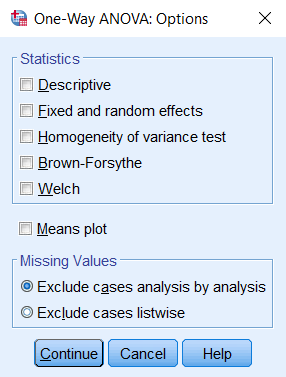
البته نحوه حذف متغیر یا مشاهداتی که دارای مقدار گمشده هستند در بخش Missing Values نیز وجود دارد. در هر یک از پنجرههای فرعی، پس از انتخاب گزینهها، با فشردن دکمه Continue به پنجره اصلی باز میگردید. با کلیک روی دکمه OK در این پنجره، عملیات محاسباتی برای آنالیز واریانس یک طرفه در SPSS اجرا خواهد شد.
حال به مثال خود باز میگردیم. همانطور که گفتیم، میخواهیم نتیجه اثر سیگار روی رکورد دو سرعت در بین دانشجویان را بسنجیم و مشخص کنیم که آیا سیگاری بودن در قدرت و سرعت دوندگی یا آمادگی جسمانی آنها تاثیر دارد یا خیر؟
حل یک مثال در آنالیز واریانس یک طرفه در SPSS
در این قسمت با استفاده از یک فایل اطلاعاتی، تکنیک تحلیل واریانس را برای اجرای آزمون برابری میانگین در بین سه گروه یا تیمار به کار میبریم. برای دسترسی به فایل اطلاعاتی در قالب sav، کافی است پرونده فشرده شده را از اینجا دریافت کرده و پس از خارج کردن از حالت فشرده، در نرمافزار SPSS باز کنید.
نکته: پروندههای اطلاعاتی با پسوند sav. مربوط به مجموعه دادههای اطلاعاتی در نرمافزار SPSS است.
ابتدا نگاهی به محتویات این فایل میاندازیم و نحوه قرارگیری دادهها و نوع آنها را مورد بررسی قرار میدهیم. در تصویر 7، محتویات فایل اطلاعاتی anovaSampleDataset.sav را مشاهده میکنید. ستونهایی که در این تحلیل به کار خواهیم بست، شامل Smoking به عنوان متغیر عامل یا فاکتور (متغیر مستقل) و متغیر وابسته نیز Sprint خواهد بود. واضح است که متغیر Smoking از نوع اسمی (Nominal) با علامت سه دایره و متغیر Sprint نیز از نوع کمی (Scale) با علامت خطکش در این پنجره ظاهر شدهاند.

در واقع به کمک این دو متغیر و مجموعه داده میخواهیم بدانیم بین سه گروه مرتبط با مصرف سیگار (غیرسیگاری = ۰، ترک سیگار = ۱ و سیگاری = ۳) از لحاظ رکورد زمانی دو سرعت، اختلافی وجود دارد یا خیر. همانطور که گفتیم، گام اول اجرای دستور آنالیز واریانس است. با توجه به پارامترها و متغیرهای مربوط به مثال، پنجره پارامترها را مطابق با تصویر ۸ مقدار دهی میکنیم.
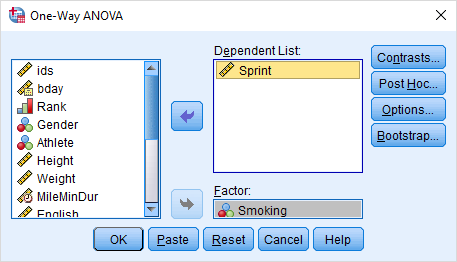
برای آنکه در صورت رد شدن فرض صفر، مقایسههای چندگانه و پس آزمونها نیز اجرا شوند، گزینههای قسمت Post Hoc را مطابق با تصویر ۹ مشخص میکنیم.
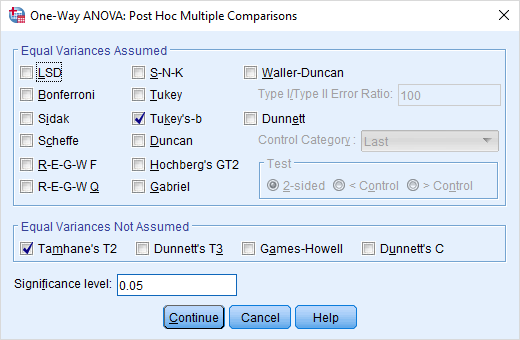
از آنجایی که هنوز نمیدانیم فرض برابری واریانسها رد یا پذیرفته شده است، گزینه Tukey's-b از قسمت فرض برابری واریانسها و Tamhane's T2 را از بخش نابرابری واریانسها انتخاب کردهایم.
نکته: فرض کنید مطالعات قبلی اطلاعاتی نسبت به انتخاب گروهها یا تیمارها و اثر گذاری آنها روی رکورد دو سرعت ندارند. در نتیجه از پیشآزمون یا «تضادها» (Contrast) استفاده نکردیم.
در بخش یا قسمت تنظیمات اختیاری گزینههای مرتبط با تحلیل واریانس یک طرفه را مطابق با تصویر ۱۰ در نظر گرفتهایم. واضح است که شاخصهای «آمار توصیفی» (Descriptive) و «آزمون برابری واریانسها» (Homogeneity of variance test) را فعال کردهایم. باز هم به علت عدم اطلاع از وضعیت یا نتیجه آزمون برابری واریانسها، گزینههای مربوط به محاسبه آمارهها Brown-Forsythe و Welch را هم انتخاب کرده تا در صورت رد فرض برابری واریانسها از آن آمارهها برای انجام آزمون آنالیز واریانس استفاده کنیم. آماره Brown-Forsythe در مقابل غیرنرمال بودن دادهها در در گروه یا تیمار نیز مقاوم (Robust) بوده و میتواند نتایج قابل قبولی ارائه دهد.
رسم نمودار مقایسه میانگینها نیز در این پنجره صورت گرفته است.
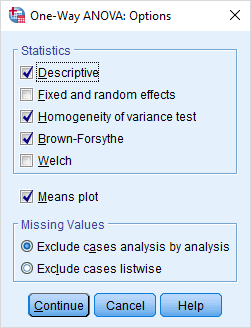
این بخش، آخرین قسمت برای اجرای آنالیز واریانس برای مثال گفته شده است. اگر میخواهید این دستورات را در محیط کد نویسی نرمافزار SPSS، یعنی محیط Syntax به کار برید، از قطعه کد زیر کمک بگیرید.
با اجرای این دستورات یا کد، خروجی تحلیل واریانس یک طرفه در SPSS ظاهر خواهد شد.
تفسیر خروجی آنالیز واریانس یک طرفه در SPSS
نتیجه اجرای آنالیز واریانس با توجه به انتخاب گزینهها و درخواستهای کاربران ممکن است با چیزی که در ادامه مشاهده میکنید تفاوت داشته باشد ولی آنچه دستور یا کدهای بخش قبلی تولید میکنند به ترتیب در ادامه مورد بررسی قرار میگیرند.
گام اول: آمار توصیفی
با توجه به تنظیمات و درخواستهایی که از دستور ANOVA در SPSS داشتیم، خروجیها به ترتیب زیر ظاهر میشوند. بخش اول که در تصویر ۱۱ قابل مشاهده است، آمار توصیفی است که شامل جدولی با ستونهایی مربوط به «تعداد» (N)، «میانگین» (Mean)، «انحراف استاندارد» (Std. Deviation)، «خطای استاندارد» (Std. Error) و «فاصله اطمینان ۹۵٪» (Confident Interval for Mean) همچنین مقدار «حداقل» (Minimum) و «حداکثر» (Maximum) است.
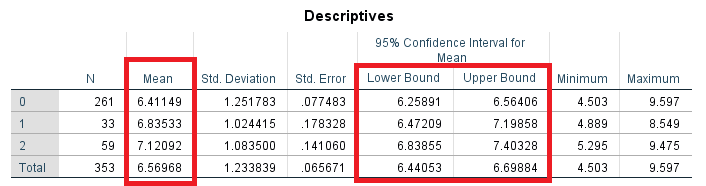
براساس فاصله اطمینان و مقادیر حاصل نیز میتوان نتیجه حدسهایی در مورد نابرابر در مقدار زمان دو سرعت دانشجویان در سه گروه مطرح کرد. به نظر میرسد که کمترین زمان رکورد سرعت مربوط به گروه غیرسیگاری و بیشترین زمان نیز در اختیار گروه سیگاریها قرار گرفته است. ولی با توجه به نمونه تصادفی گرفته شده باید برای اثبات این نظریه، دست به انجام آزمون آماری یا همان تحلیل ANOVA زد.
گام دوم: آزمون برابری واریانسها
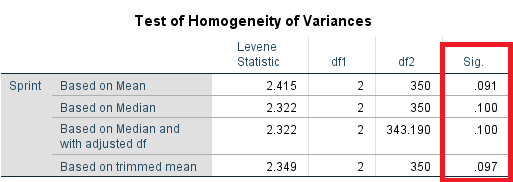
یکی از روشهای سنجش و انجام آزمون برابری واریانسها، استفاده از آماره لون و آزمون مربوط به آن است. در جدولی که در تصویر ۱۲ دیده میشود، آزمون مربوط به برابری واریانسها صورت گرفته که با توجه به کادر قرمز رنگ، براساس هر شاخصی مرکزی (مثل میانگین-mean، یا میانه-Median) واریانس یا پراکندگی حول نقاط مرکزی، در بین گروه یا تیمارها، یکسان تلقی شده است. مشخص است که برای همه حالتها مقدار .Sig یا همان مقدار احتمال (p-value)، بزرگتر از مقدار احتمال خطای نوع اول () است. در نتیجه فرض برابری واریانسها (با به شکل دقیق، پراکندگیها) رد نمیشود.
گام سوم: جدول تحلیل واریانس
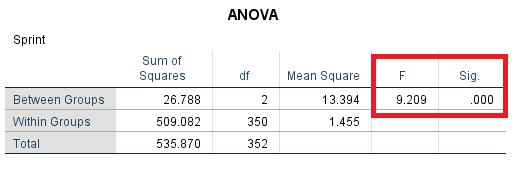
بخش و قسمت مهم در تحلیل واریانس، جدول آنالیز واریانس یا ANOVA است. در ستون آخر و همچنین ستون F که در تصویر ۱۳ دیده میشود، مشخص است که فرض صفر یعنی برابری میانگین در بین سه گروه یا تیمار رد میشود.
مقدار .sig کمتر از ۰٫۰۵ بوده در نتیجه حداقل یکی از گروهها با دیگران از لحاظ آماری به طور معنیدار اختلاف دارد.
حال بهتر است به دنبال پس آزمونها رفته و مشخص کنیم دقیقا کدام گروه باعث ایجاد اختلاف است. این کار را در گام پنجم و با توجه به خروجیهای بدست آمده انجام خواهیم داد.
گام چهارم: آزمون پرتوان برای تحلیل واریانس
از آنجایی که فرض برابری واریانسها رد نشده و آزمونهای نرمالیتی نشانگر نرمال بودن دادهها است، احتیاجی به این بخش نخواهیم داشت ولی با توجه به گزینههای انتخابی در آزمون، خروجی طبق تصویر ۱۴ ظاهر خواهد شد. واضح است که در این حالت نیز فرض صفر آنالیز واریانس رد شده و این آزمون هم رای به نابرابری حداقل یکی از میانگینها با میانگین بقیه گروهها میدهد.
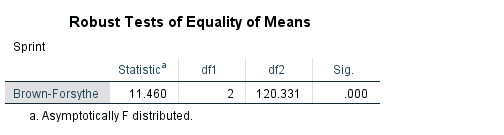
گام پنجم: تحلیل پس آزمونها
روش یا تکنیک «پس آزمون توکی» (Tukey's b) یکی از روشهای مناسب برای اجرای پس آزمون است، بطوری که علاوه بر کنترل سطح خطای آزمونهای همزمان، گروههای همسان و متجانس را هم معرفی میکند. جدول مربوط به تصویر 15، نشان میدهد که گروه غیر سیگاری و گروه کسانی که سیگار را ترک کردهاند از نظر رکورد زمانی در دو سرعت، یکسان هستند ولی گروه سیگاریها با گروه غیر سیگاری، اختلاف معنیداری از لحاظ آماری دارند، زیرا برای گروه ۰ و 2 مقدار .sig برابر با ۰٫000 شده. از طرفی برای گروه ۱ و ۲ مقدار .sig حدود ۰٫۵۱۳ بوده که نشانگر یکسان بودن میانگین در بین این دو گروه است. همچنین گروه ۰ و ۱ نیز یکسان به نظر میرسند زیرا .sig برایشان برابر با ۰٫۱۰۰ بوده که باعث میشود فرض صفر (برابری میانگین این دو گروه) رد نشود.
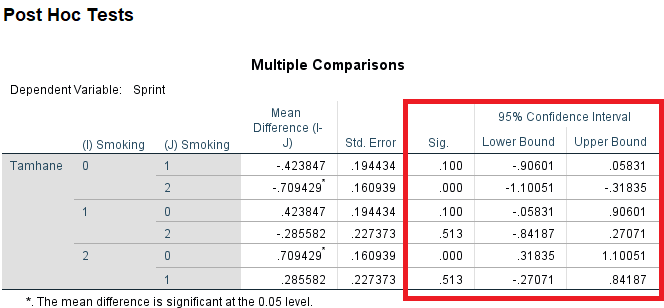
همچنین در انتهای این خروجی، گروههای همگن مشخص شده است. به جدول ظاهر شده در تصویر 16 توجه کنید. مشخص است که گروه ۰ و ۱ همسان بوده و از طرفی گروه ۱ و ۲ نیز همسان هستند. توجه داشته باشید که گروه ۱ در این بین نقش میانجی را بازی نکرده و نمیتوان نتیجه گرفت که با توجه به وجود همسانی بین دو گروه ابتدایی و انتهایی، گروه ۰ و ۲ نیز یکسان هستند. در حقیقت رابطه ارائه شده در گزارش همسانی توکی، دارای «خاصیت ترایایی» (Transitive) یا «تعدی» نیست.

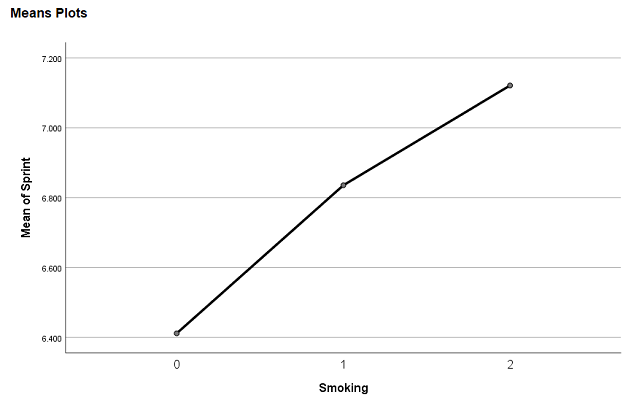
گام ششم: نمودار مقایسه میانگینها در آنالیز واریانس در SPSS
بخش انتهایی در خروجی SPSS، اختصاص به نمودار مقایسهای برای میانگین هر گروه دارد. با توجه به تصویر ۱۷، به نظر میرسد که میانگین در بین این سه گروه (با حفظ اولویت) به صورت یک رابطه خطی (Linear) تغییر میکند. یعنی اگر لازم بود که از یک تضاد (Contrast) بهره ببریم، شاید رابطه خطی مناسبترین گزینه برای تفکیک میانگینها در بین سه گروه را اختیارمان قرار میداد. واضح است که محور افقی در این نمودار گروه یا تیمارها را نمایش داده و محور عمودی نیز به مقدار یا میزان زمان مربوط به رکورد دو سرعت (برحسب ثانیه) اختصاص دارد. هر چه زمان کوتاهتر یا کوچکتر باشد، سرعت فرد و در نتیجه سیستم تنفسی و آمادگی جسمانی بهتری دارد.
خلاصه و جمعبندی
در این نوشتار به کمک مراحل و گامهای مشخص شده، تحلیل یا آنالیز واریانس یک طرفه در SPSS را اجرا و نتایج حاصل را تفسیر کردیم. همانطور که خواندید، به کارگیری آنالیز واریانس یا ANOVA دارای شرطهایی است که بعضی از آنها پس از انجام آزمون نیز باید مورد بررسی قرار گیرند تا صحت نتایج بدست آمده، مشخص شود. برای کسب اطلاعات بیشتر در این زمینه بهتر است نوشتار تحلیل واریانس اندازه مکرر یک طرفه در SPSS | راهنمای گام به گام را مطالعه کنید. در انتها نیز خروجی حاصل از تحلیل واریانس در محیط SPSS، براساس یک فایل اطلاعاتی تفسیر و نتیجه آزمون یا تحلیل واریانس مشخص شد. به این ترتیب متوجه شدیم که در بین گروه سیگاری و غیرسیگاری، بخصوص تفاوت معنیداری در زمان رکورد دو سرعت وجود دارد.













باسلام
لطفا بفرمائید دلیل اینکه در آزمون آنالیز واریانس در تکرار مشاهدات، عدد آماره F خیلی زیاد می شود چه میتواند باشد؟ آیا فقط تفاوت زیاد نمره گروه ها میتواند این موضوع را باعث شود یا مشکلی در تحلیل داده ها وجود داشته است؟
ممنونم
سلام.درود بر شما پیوستگی مطالب با ترتیب بسیار دقیق و منظمی ارائه داده شده بود که موجب درک بهتر آن شد…متشکرم. راهتان هموار
سلام. درود بر شما. بسیار شیوا، رسا و عالی و کاربردی توضیح دادید. خدا به شما اجر دهد که به این زیبایی بذل علم می کنید.
عالی
چقدر عالی و کاربردی نوشته بودید مرسی
بسیار ممنون و متشکرم
خداقوت خدمت استاد عزیز و نگارندگان محترم
واقعا استفاده کردیم. مطالب بسیار اموزنده و مفید در متن بود که در خیلی از کلاسهای درس دانشگاه یافت نمی شود…
خداوند جزای خیر و سلامتی و عاقبت بخیری به شماها عطا کند