آزمون Z در آمار — به زبان ساده

آزمون‌های آماری بسیار متنوع بوده و تحت شرایط مختلف باید نسبت به انتخاب هر یک اقدام کرد. این شرایط می‌تواند بسته به نوع داده یا توزیع آن‌ها تغییر کند. بنابراین شناخت هر آزمون و شرایط اجرای آن برای کسانی که به تحلیل داده و آزمون‌های آماری می‌پردازند، امری مهم محسوب می‌شود. در این نوشتار با آزمون Z در آمار آشنا شده و کاربردهای آن را با ذکر مثال‌هایی پی‌ می‌گیریم.

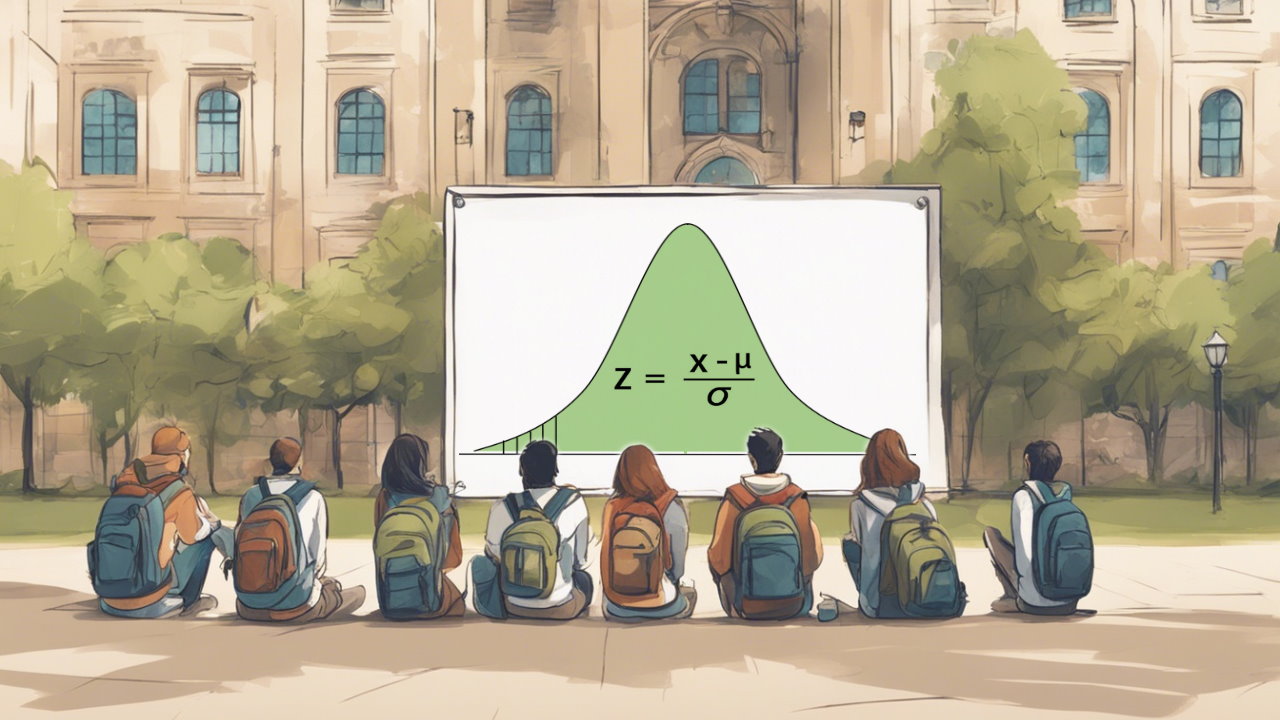
برای آشنایی بیشتر با اصطلاحات به کار رفته در این متن بهتر است با موضوعات استنباط و آزمون فرض آماری و p- Value آشنایی داشته باشید. همچنین اطلاع از توزیع نرمال و متغیر تصادفی آن و فاصله اطمینان نیز خالی از لطف نیست.

آزمون Z در آمار

اگر آماره مربوط به یک آزمون آماری، تحت فرض صفر، دارای توزیع نرمال (Normal Distribution) باشد، می‌توان از آزمون Z برای تصمیم نسبت به رد یا تایید فرضیه‌های آماری کمک گرفت.

فیلم آموزش آمار استنباطی برای مدیریت و علوم انسانی در فرادرس

کلیک کنید

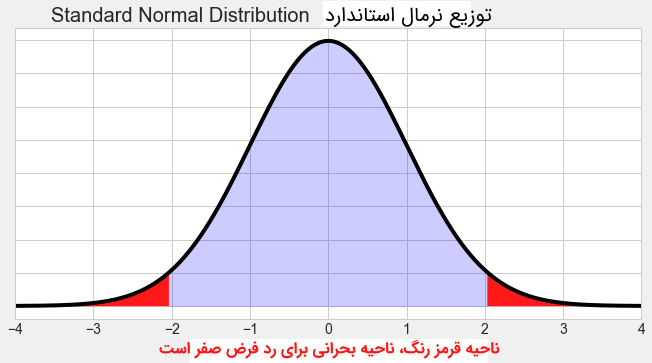
آماره Z، در هر سطح معنی‌داری برای آزمون Z، برای پارامتر مرکزی توزیع، یک مقدار بحرانی دارد. همچنین برای ایجاد «فاصله اطمینان» (Confidence Interval) برای پارامتر مکان (مانند میانگین)، یک مقدار بحرانی در نحوه تشکیل فاصله اطمینان قابل استفاده است. برای مثال در سطح خطای ۵٪ برای آزمون دو طرفه، مقدار بحرانی Z برابر با ۱٫۹۶ است. در حالیکه مقدار بحرانی آزمون t وابسته به اندازه نمونه ($$n$$) بوده و با توجه به حجم نمونه یا در حقیقت همان «درجه آزادی» (Degree of Freedom)، مقدار بحرانی تعیین می‌شود. این موضوع یک مزیت برای آزمون Z نسبت به آزمون مشابه آن یعنی آزمون t محسوب می‌شود.

از طرفی با توجه به «قضیه حد مرکزی» (Central Limit Theorem)، بسیاری از توزیع‌ها، تحت شرایطی مشخص، به سمت توزیع نرمال میل می‌کنند. البته یکی از مهمترین شرط‌ها در قضیه حد مرکزی، بزرگ بودن حجم نمونه است. بنابراین بسیاری از آزمون‌های آماری یا در حقیقت توزیع آماره آزمون می‌توانند با توزیع نرمال یکسان در نظر گرفته شوند به شرطی که اندازه نمونه بزرگ و واریانس جامعه نیز معلوم باشد.

البته اگر واریانس جامعه نیز نامشخص بوده ولی از متناهی بودن آن آگاه باشیم و از طرفی حجم نمونه نیز کمتر از ۳۰ باشد، جایگزین برای آزمون Z، همان آزمون و آماره t است.

در ادامه نحوه اجرای آزمون Z و گام‌های آن، برای آماره‌ یا برآوردگری به شکل T با توزیع تقریبا نرمال تحت فرض صفر گفته خواهد شد. البته از آنجایی که پارامتر مرکزی اغلب میانگین در نظر گرفته می‌شود، برآوردگر برای میانگین جامعه را می‌توان همان میانگین نمونه‌ای یا $$\overline{X}$$ محسوب کرد.

• گام اول: ابتدا مقدار مورد انتظار یا همان امید ریاضی (Expected Value) برای آماره T را تحت فرض صفر مشخص کنید. همچنین در صورت نامعلوم بودن واریانس، برآورد برای واریانس این برآوردگر نیز لازم است.
• گام دوم: با توجه به یک طرفه یا دو طرفه بودن فرض‌های صفر و مقابل، وضعیت و خصوصیات آماره T را بررسی کنید. اگر فرض صفر به صورت $$H_0 : \mu \geq \mu_0$$ و فرض مقابل نیز به شکل $$H_1 : \mu < \mu_0$$ باشد، آزمون به صورت یک طرفه-بالا/راست (Upper/Right - tailed) است. همچنین در حالتی که فرض صفر به شکل $$H_0: \mu \leq \mu_0$$ و فرض مقابل نیز $$H_1: \mu \geq \mu_0$$ باشد، آزمون از نوع یک طرفه- پایین/چپ (Lower/Left - tailed) است. در صورت نمایش فرض صفر به صورت $$H_0 : \mu = \mu_0$$ در مقابل $$H_1: \mu \neq \mu_0$$ یک آزمون دو طرفه (Two tailed) مورد نظر است.
• گام سوم: مقدار آماره آزمون یعنی همان امتیاز استاندارد را براساس میانگین و انحراف استاندارد برآورد شده بدست می‌آوریم. در اینجا آماره آزمون Z خواهد بود.

$$\large Z = \dfrac{\overline{X} - \mu_0}{s}$$

• گام چهارم: براساس این که آزمون یک طرفه یا دو طرفه است، مقدار احتمال (p-Value) را برای آزمون بالا/راست به صورت $$\phi(Z)$$ و برای آزمون پایین/چپ از $$\phi(-Z)$$ استفاده می‌کنیم. همچنین برای آزمون دو طرفه هم مقدار احتمال را براساس $$2 \phi(-|Z|)$$ بدست خواهیم آورد.

نکته: منظور از $$\phi(Z)$$، مقدار تابع توزیع تجمعی نرمال استاندارد (Standard Normal Cumulative Distribution Function) در نقطه $$Z$$ است.

آزمون Z و بررسی پارامتر مکان توزیع

اغلب آزمون Z در آمار مرتبط با آزمون تک نمونه‌ای برای پارامتر مکان (One-sample location test) یا همان میانگین است. توسط این آزمون، میانگین یک مجموعه از مقادیر با یک مقدار ثابت یا حدس اولیه برای پارامتر مکان (میانگین) یک توزیع، مقایسه و مورد آزمون آماری قرار می‌گیرد. البته باید توجه داشت که واریانس برای جامعه نیز معلوم است و تنها پارامتر نامشخص برای جامعه میانگین است.

فیلم آموزش آمار و احتمال مهندسی – جامع و با مثال های مختلف در فرادرس

کلیک کنید

برای مثال فرض کنید که $$X_1 , X_2 , \ldots, X_n$$ نمونه‌ای مستقل و هم توزیع از یک جامعه هستند که میانگین آن $$\mu$$ بوده و واریانس نیز معلوم و برابر با $$\sigma^2$$ است. ویژگی‌های آماره آزمون برای آزمونی به شکل زیر را در ادامه فهرست کرده‌ایم.

$$\large \begin{cases}H_0 : & \mu = \mu_0 \\ H_1: & \mu \neq \mu_0 \end{cases}$$

• ویژگی اول: مقدار مورد انتظار برای برآوردگر میانگین (در اینجا $$\overline{X}$$) تحت فرض صفر برابر است با $$\mu_0$$، همچنین واریانس برای این برآوردگر (با فرض معلوم بودن واریانس جامعه) به صورت $$\frac{\sigma^2}{n}$$ خواهد بود.
• ویژگی دوم: با توجه به فرض صفر می‌توان میانگین نمونه‌ای $$\overline{X}$$ را آماره آزمون در نظر گرفت. در این صورت اگر $$\overline{X} - \mu_0$$ بزرگ باشد، فرض صفر رد خواهد شد.
• ویژگی سوم: مقدار آماره Z را طبق رابطه زیر محاسبه می‌کنیم. با توجه به معلوم بودن واریانس، واریانس برآوردگر نیز به شکل $$S^2 = \frac{\sigma^2}{n}$$ در خواهد آمد. پس خواهیم داشت:

$$\large Z = \dfrac{\overline{X} - \mu_0}{\dfrac{\sigma}{\sqrt{n}}}$$

• ویژگی چهارم: اگر اندازه نمونه بزرگ باشد، طبق قضیه حد مرکزی می‌توان توزیع $$Z$$ را نرمال در نظر گرفت و از آزمون Z استفاده کرد. البته شرط معلوم بودن واریانس نیز در این حالت وجود دارد. اگر اندازه نمونه بزرگ بوده ولی واریانس معلوم نباشد، باز هم می‌توان از واریانس نمونه‌ای به عنوان برآوردگر استفاده کرده و آماره آزمون را نرمال استاندارد در نظر گرفت. اگر حجم نمونه کوچک بوده و واریانس نیز توسط نمونه برآورد شده باشد، توزیع آماره آزمون را توزیع t‌ در نظر می‌گیریم.
• ویژگی پنجم: با توجه به مقادیر نمونه، آماره آزمون را محاسبه کرده و با مقدار بحرانی آزمون دو طرفه مقایسه می‌کنیم. اگر $$|Z|$$ بزرگتر از مقدار $$Z_{1-\alpha/2}$$ بود، فرض صفر در آزمون دو طرفه رد می‌شود.

البته می‌توان برای تصمیم نسبت به رد یا تایید فرض صفر، از مقدار احتمال (p-Value) نیز کمک گرفت که در این صورت احتیاجی به مقدار خطای نوع اول $$\alpha$$ نخواهیم داشت.

یک مثال عددی

فرض کنید در یک مدرسه، میانگین و انحراف معیار نمرات امتحان زبان فارسی ۱۰۰ و ۱۲ نمره باشد. نمره ۵۵ دانش آموز به عنوان نمونه انتخاب شده و میانگین نمره ‌‌آن‌ها ۹۶ محاسبه شده است. آیا می‌توان گفت که متوسط (میانگین) نمره امتحان زبان فارسی کمتر از ۱۰۰ است. یا به بیان دیگر آیا این دانش آموزان به جامعه‌ای دیگر نسبت بقیه دانش آموزان مدرسه تعلق دارند؟ فرض بر این است که جامعه نمرات امتحان زبان فارسی دارای توزیع نرمال است.

توجه داشته باشید که در اینجا فرض‌های آماری به صورت زیر خواهند بود.

$$\large \begin{cases}H_0 :& \mu = \mu_0 \\ H_1 :& \mu \neq \mu_0 \end{cases}$$

در نتیجه با یک آزمون دو طرفه مواجه هستیم. حال گام‌های مربوط به آزمون Z در آمار را به کار می‌بریم.

گام اول: محاسبه آماره و میانگین و انحراف استاندارد آن: همانطور که گفته شد، $$\overline{X}$$  برآورد مورد نظر برای $$\mu$$ یا همان پارامتر مکان توزیع نرمال است. در نتیجه امید ریاضی $$\overline{X}$$‌ برابر با $$\mu_0$$ تحت فرض صفر است.

همچنین انحراف استاندارد (خطای برآوردگر) برای برآوردگر $$\overline{X}$$ به صورت زیر حاصل می‌شود.

$$\large {\mathrm {SE}} = {\frac {\sigma }{{\sqrt n}}} = {\frac {12}{{ \sqrt {55}}}} = {\frac {12}{7.42}} = 1.62\,\!$$

به یاد دارید که انحراف معیار جامعه مورد نظر $$\sigma=12$$ بوده است.

گام دوم: محاسبه مقدار آماره آزمون Z: با تقسیم اختلاف میانگین از میانگین جامعه (تحت فرض صفر) و تقسیم آن بر خطای استاندارد، آماره آزمون Z بدست می‌آید.

$$\large z = {\dfrac {\overline{X} - \mu_0 }{{\mathrm {SE}}}} = {\dfrac {96 - 100}{1.62}} = -2.47 \,\!$$

در این مثال، میانگین نمره کلاس برابر با ۹۶، خطای استاندارد 1٫62 و همچنین مقدار آماره آزمون برابر با ۲٫۴۷- است. خطای میانگین نمونه‌ای از میانگین واقعی برحسب واحد خطای استاندارد، برابر با ۲٫۴۷- تحت فرض صفر است. با توجه به مقدار Z در جدول توزیع نرمال استاندارد، مشخص می‌شود که احتمال مشاهده مقداری کمتر از ۲٫۴۷- تقریبا برابر با 0٫0068 است. پس این اتفاق (با توجه به صحت فرض صفر) خیلی به ندرت پیش می‌آید.

گام سوم: مقایسه و تصمیم نسبت به رد یا تایید فرض صفر: مقدار بدست آمده در گام قبلی مربوط به آزمون Z یک طرفه است. در نتیجه باید آن را دو برابر کرده تا نسبت به نتیجه آزمون دو طرفه براساس p-value به نتیجه صحیح برسیم. در نتیجه ۰٫۰۰۶۸ × ۲ = 0٫014 حاصل شده که با توجه به مقدار ۰٫۰۵ برای $$\alpha$$، فرض صفر رد می‌شود و می‌توان گفت که میانگین نمرات این درس، تفاوت معنی‌دار با ۱۰۰ دارد.

به بیان دیگر نتیجه می‌گیریم که با احتمال 0٫014 - 1 = 0٫986، نمونه تصادفی ۵۵ تایی از این مدرسه دارای میانگینی با اختلاف ۴ واحد از میانگین جامعه هستند. همچنین با ۹۸٫۶ اطمینان فرض برابری میانگین با ۱۰۰ رد شده فاصله اطمینان تولید شده توسط نمونه، شامل میانگین جامعه یعنی ۱۰۰ نخواهد بود.

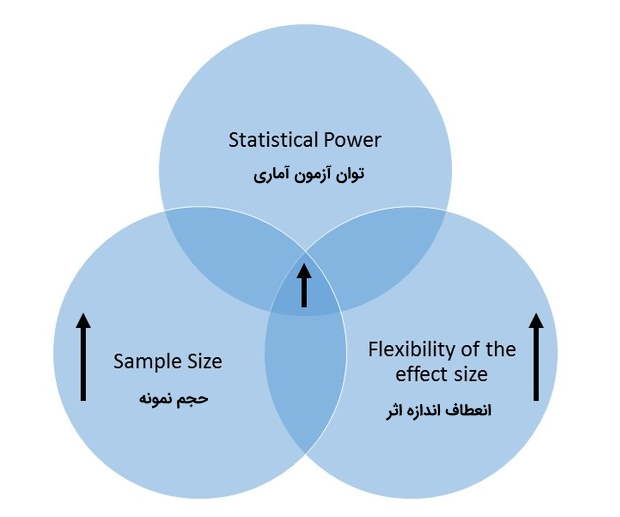
نکته: این آزمون نشان می‌دهد که نمونه ۵۵ تایی از دانش‌آموزان به طور نامعمولی با جامعه مورد نظر، تفاوت دارند. متاسفانه این تحلیل نمی‌تواند «اندازه اثر» (Effect size) با مقدار ۴ امتیاز اختلاف را معنی کند. مثلا اگر به جای یک کلاس، یک ناحیه آموزش و پرورش را به عنوان نمونه ۹۰۰ تایی در نظر می‌گرفتیم، که میانگین نمرات آن‌ها ۹۹ بود، باز هم مقدار احتمال و آماره آزمون تقریبا یکسانی حاصل می‌شد. این موضوع نشان می‌دهد که اگر اندازه نمونه به  اندازه کافی بزرگ باشد، اختلاف‌های کوچک نسبت به فرض صفر، اغلب یا تقریبا همیشه، معنی‌دار می‌شوند.

شرایط استفاده از آزمون Z

در قسمت‌های قبلی، مهم‌ترین شرط‌های استفاده از آزمون Z را بازگو کردیم. در این بخش نیز با تاکید بیشتر این شرایط را مورد بررسی قرار می‌دهیم.

فیلم آموزش آمار و احتمالات مهندسی – حل نمونه سوالات کنکور ارشد در فرادرس

کلیک کنید

پارامتر مزاحم در آزمون Z (مانند واریانس یا پارامتر مقیاس، برای آزمون پارامتر مکان) باید معلوم بوده یا حداقل با دقت زیاد، برآورد شده باشد. آزمون Z بر یک پارامتر که اغلب پارامتر مکان است متمرکز شده و پارامترهای نامعلوم دیگر جامعه آماری را ثابت فرض می‌کند.

به این ترتیب طبق «قضیه اسلاتسکی» (Slutsky's Theorem) می‌توان به کمک «برآوردگر سازگار» (Consistent Estimator) پارامتر نامعلوم مزاحم را به شکل کارایی برآورد کرد. در حقیقت به این ترتیب یک برآوردگر مجانبی یا تقریبی بدست آمده است که می‌تواند با تقریب مناسب، پارامتر مزاحم را برآورد کند. البته «قضیه اسلاتسکی» به بزرگ بودن حجم نمونه نیز اشاره دارد. در نتیجه اگر حجم نمونه کوچک باشد، استفاده از آزمون Z موثر و دقیق نخواهد بود.

آماره آزمون باید دارای توزیع نرمال باشد. در حالت کلی با توجه به «قضیه حد مرکزی» (Central Limit Theorem) می‌توان به طور تقریبی بیشتر توزیع‌های متقارن را با توزیع نرمال تقریب زد. یک روش برای مشخص کردن آن، نمونه‌گیری‌های متعدد و ترسیم نمودار تغییرات مقدار برآوردگر و مقایسه آن با نمودار نرمال است. در صورتی که آماره دارای توزیع، تقریباً نرمال نباشد، استفاده از آزمون Z با خطای زیاد همراه خواهد بود و توان آزمون کاهش خواهد یافت.

نکته: در چنین شرایطی یک جایگزین مطمئن برای آزمون Z، آزمون t‌ خواهد بود. البته شاید روش‌های ناپارامتری نیز در این زمینه کارا باشند.

آزمون Z و برآورد حداکثر درستنمایی

همانطورکه در این متن اشاره شد، آزمون‌های مربوط به پارامترهای مکان، از معروف‌ترین آزمون‌های Z هستند. ولی آزمون Z را برای «برآورد حداکثر درستنمایی» (Maximum Likelihood Estimation) نیز می‌توان به کار برد. در دیگر نوشتارهای مجله فرادرس با نحوه برآورد پارامتر به کمک روش حداکثر درستنمایی آشنا شده‌اید. برآوردهای حداکثر درستنمایی به طور مجانبی و تحت شرایطی دارای توزیع نرمال هستند. همچنین محاسبه واریانس مجانبی نیز برای آن‌ها به کمک عبارت «اطلاع فیشر» (Fisher Information) امکان‌پذیر است.

به این ترتیب اگر برآوردگر حداکثر درستنمایی را به خطای استاندارد (Standard Error) آن تقسیم کنیم، به یک آماره آزمون مناسب با توزیع نرمال تحت فرض صفر خواهیم رسید. بطور کلی اگر $$\widehat{\theta}$$ برآوردگر حداکثر درستنمایی برای پارامتر $$\theta$$ باشد و $$\theta_0$$‌، مقدار این پارامتر تحت فرض صفر در نظر گرفته شود، رابطه زیر به عنوان آماره آزمون Z قابل استفاده است.

$$\large ({\hat {\theta }} - \theta_{0}) / {{\rm {SE}}}({\hat {\theta }})$$

به یاد داشته باشید که در اینجا هم فرض بزرگ بودن حجم نمونه برای برآوردگر حداکثر درستنمایی و داشتن توزیع نرمال برای آماره آزمون، وجود دارد. در صورتی که حجم نمونه به اندازه کافی بزرگ نباشد، فرض نرمال بودن ممکن است گمراه کننده شود.

فیلم آموزش آمار و احتمال مهندسی – حل تمرین و تست کنکور ارشد در فرادرس

کلیک کنید

تعیین حجم نمونه برای صدق کردن برآوردگر و آماره آزمون حداکثر درستنمایی، در شرط نرمال بودن، کار ساده‌ای نیست. معمولا این کار با به کمک شبیه‌سازی صورت گرفته و حداقل میزان نمونه لازم برای صحت این فرض استخراج می‌شود.

اگر توزیع آماره آزمون تحت فرض صفر قابل تعیین نبوده یا حداقل توزیع آن، نرمال نباشد، بهتر است از «روش‌ها و آزمون‌های ناپارامتری» (Non-Parametric Method) مانند آماره U استفاده کرد.

خلاصه و جمع‌بندی

در این نوشتار با آزمون Z در آمار و همچنین آماره این آزمون و شرایط به کارگیری آن آشنا شدیم. همانطور که خواندید، در زمانی که برآوردگر درستنمایی استفاده می‌شود، برای آزمون مربوط به برابری برآوردگر با پارامتر نیز می‌توان از آزمون Z استفاده کرد. البته شرط بزرگ بودن اندازه نمونه و توزیع تقریبا نرمال برای برآوردگر، از شرایطی است که در این حالت باید در نظر گرفت.

هر چند شرایط مربوط به آزمون Z سختگیرانه است ولی اگر این شرط‌ها در جامعه آماری محقق شده باشد، پرتوان‌ترین آزمون نسبت به آزمون‌های مشابه نصیبان خواهد شد و نتایج بدست آمده نسبت به رد یا تایید فرضیه‌های آماری، بسیار به واقعیت نزدیک خواهند بود.