جامعه آماری – انواع داده و مقیاسهای آنها
اغلب با مفهومی به نام جامعه آماری و انواع دادههای آن برخورد داشتهاید. وقتی در مورد موضوعی تحقیق میکنید، یا میخواهید دست به سرشماری یا نمونهگیری بزنید باید جامعه آماری شما مشخص باشد.

جامعه آماری
مشخصات و اطلاعات مربوط به موضوعی که در مورد آن تحقیق و بررسی انجام میدهید، جامعه آماری شما را تشکیل میدهند. در جامعه آماری هر شی یا فرد دارای خصوصیات یا ویژگیهای مشترکی با دیگر افراد است در غیر اینصورت امکان جمع شدنشان در یک جامعه وجود نداشت. پس جامعه آماری باید طوری تعریف شود که بتوان اعضای آن را مشخص کرد. ممکن است تعداد اعضای جامعه آماری بسیار زیاد باشند ولی باید روشی برای سنجش عضویت یک شی در آن جامعه به همراه ویژگیهایش وجود داشته باشد، در غیراینصورت جامعه آماری نامشخص است.
برای مثال وقتی در مورد مسئله میزان رضایت کارکنان شرکت X در سال ۱۳۹۷ تحقیق میکنید، جامعه آماری شما کارکنان آن شرکت در سال ۱۳۹۷ هستند که میزان رضایت آنها توسط روشهایی قابل اندازهگیری است. پس همه در متغیر رضایت شغلی مشترک هستند ولی مقدار این متغیر برای هر نفر با نفر دیگر متفاوت است.

یا اگر در مورد تغییرات رشد قد کودکان ۳-۵ سال در یک دوره ۱۰ ساله تحقیق میکنید، محدوده زمانی تهیه اطلاعات و افرادی که باید مورد سنجش قد قرار بگیرند مشخص شده است و جامعه آماری شما را تشکیل میدهند.
جامعه آماری متناهی و نامتناهی
اگر اعضای جامعه آماری و انواع دادههای آن قابل شمارش و با پایان باشد، یک جامعه آماری متناهی دارید. مثالهای بالا نمونهای از جامعه آماری متناهی بود. ولی زمانی که اعضاء جامعه آماری، تعدادی نامعلوم داشته باشند جامعه آماری را نامتناهی مینامیم. برای مثال تعداد پرتاب یک سکه تا مشاهده شیر، ممکن است تا ابد طول بکشد. در این حالت با یک جامعه آماری نامتناهی مواجه هستیم زیرا تعداد اعضای این جامعه آماری نامشخص است.
متغیر، صفت یا ویژگی
به ويژگی كه از افراد يا اشياء جامعه آماری اندازهگيری میشود و مقدارش از عضوی به عضو ديگر متفاوت است، «متغير» (Variable) میگويند. معمولاً متغیر را با حروف انگليسی مانند X ،Y و Z نشان میدهند.
پس از اندازهگيری مقادير متغيرها در جامعه آماری، دادههای آماری بدست میآيد. اگر مقدارهای اندازهگیری شده از جامعه آماری به صورت کیفی باشند، گاهی از نام «صفت» (Attribute) یا «ویژگی» (Feature) نیز به جای متغیر استفاده میشود.
مقدارهای کمی
این دسته از مقدارها از طریق شمارش یا سنجش با ابزارهای اندازهگیری بدست میآیند. این نوع دادهها بوسیله اعداد نمایش داده میشوند. مانند طول، وزن، فشار، دما و ...
از آنجایی این نوع دادهها به صورت عددی هستند امکان انجام محاسبات ریاضی روی آنها وجود دارد. پس میتوان میانگین، واریانس و دیگر شاخصهای آماری را از روی آنها محاسبه کرد. در بیشتر مواقع متغیرهای مربوط به جامعه آماری از نوع کمی هستند.
مقدارهای کیفی
به دسته دیگر از مقدارها که برعکس دادههای کمی از طریق شمارش یا اندازهگیری بدست نمیآیند، دادههای کیفی میگویند. این نوع دادهها اغلب با صفت یا ویژگی در جامعه آماری در رابطه هستند. از این مقدارها به منظور طبقهبندی یا دستهبندی جامعه آماری میتوان استفاده کرد.

ویژگیهایی نظیر محل تولد، گروه خون، رنگ مورد علاقه و ... از نوع دادههای کیفی هستند. البته گاهی در مورد مقدار هر یک از ویژگیهای کیفی ممکن است سلیقه نیز موثر باشد و برای یک عضو از جامعه آماری دو یا چند مقدار برای ویژگی کیفی آن بدست آید. برای مثال نرمی پارچه ممکن است از دید یک نفر مقداری برابر با زبر داشته باشد ولی فرد دیگر آن را با زبری متوسط مقدار دهی کند.
ویژگیهای جامعه آماری و انواع دادههای آن که به شکل کیفی هستند، معمولا به صورت متنی ثبت میشوند. ولی اغلب برای استفاده از دادههای کیفی، آنها را به صورت عددی نمایش میدهیم. این کار به مفهوم انجام محاسبات روی آنها نیست. بلکه این اعداد فقط کدهایی برای نمایش مقدارهای کیفی هستند.
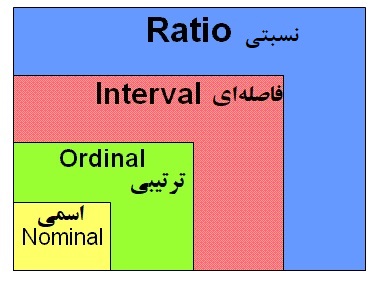
مقیاسهای اندازهگیری برای متغیرهای کمی
جامعه آماری و انواع دادههای آن را که به صورت کمی هستند، با توجه به نوع خصوصیات و مقدار آنها به دو گروه تقسیم میکنند: ۱- «مقیاس فاصلهای» (Interval Scale) و ۲- «مقیاس نسبتی» (Ratio)
۱- دادههای با مقیاس فاصلهای: اگر مقدارهای متغیر اندازهگیری شده به شکلی باشد که صفر در آن مقداری قراردادی محسوب شود، آن نوع دادهها را با مقیاس فاصلهای میشناسند. نسبت تفاضل بین دو مقدار با واحدهای مختلف در این مقیاس حفظ میشود. دادههای مربوط به دما، زمان و ... از نوع فاصلهای هستند. با استفاده از تبدیلات خطی میتوان مقداری با یک واحد اندازهگیری را به واحد دیگر تبدیل کرد.
برای مثال فرض کنید دمای چهار جسم را با استفاده از سانتیگراد اندازه گرفتهایم. اگر تفاضل دمای جسم اول با دوم دو برابر تفاضل دمای جسم سوم و چهارم با واحد سانتیگراد باشد این نسبت براساس واحد اندازهگیری فارنهایت نیز حفظ میشود. این محاسبات در مثال زیر آمده است.
مثال
دمای چهار جسم بر حسب سانتیگراد به ما داده شده است: دمای جسم اول=25، دمای جسم دوم=35، دمای جسم سوم= 50 و دمای جسم چهارم= 70. در این حالت نسبت تفاضل دمای جسم اول و دوم با جسم سوم و چهارم را برحسب سانتیگراد محاسبه میکنیم. . حال دما برای جسمها برحسب فارنهایت: دمای جسم اول=77، دمای جسم دوم=95، دمای جسم سوم= 122 و دمای جسم چهارم= 158. در این حالت نسبت تفاضل دمای جسم اول و دوم با جسم سوم و چهارم را برحسب فارنهایت محاسبه میکنیم. . در نتیجه با تغیر واحد اندازهگیری از سانتیگراد به فارنهایت نسبت تفاضل (فاصلهها) تغییری نکرد.
دقت کنید که دمای جسم سوم دو برابر دمای جسم اول در واحد سانتیگراد است، در حالیکه در واحد فارنهایت نسبت دمای جسم سوم به اول حدود 1.6 برابر است.
۲- دادههای با مقیاس نسبتی: در این حالت جامعه آماری و انواع دادههای آن مقدارهای اندازهگیری شدهای مانند مقیاس فاصلهای بوده به صورت عددی هستند ولی صفر به معنی هیچ است. طول، وزن و ... دادههایی با مقیاس نسبتی هستند.
در دادههای فاصلهای این مسئله وجود دارد که صفر مقداری قراردادی است و به معنی عدم وجود مقدار نیست. برای مثال اگر دما را با درجه سانتیگراد در نظر بگیرم، میدانیم که صفر درجه سانتیگراد به معنی بدون داشتن دما نیست و حتی مقدارهای منفی نیز برای آن وجود دارد. ولی طول به اندازه صفر سانتیمتر به معنی عدم داشتن طول است.
مثال
با توجه به خاصیت دادهها با مقیاس نسبتی، نسبت دو مقدار مثلا طول قد دو فرد با واحد سانتیمتر با نسبت دو مقدار با واحد دیگر مثلا طول همان دو فرد با واحد اینچ، یکی خواهد بود. اگر قد نفر اول برابر با ۱۶۰ سانتیمتر و قد نفر دوم نیز ۱۷۰ سانتیمتر باشد، نسبت قد نفر اول به دوم برابر با 0.94 خواهد بود. با تبدیل مقدارها به واحد اینچ، نفر اول قدی برابر با 62.99 و نفر دوم قدی برابر با 66.92 خواهد داشت. نسبت این دو قد باز هم برابر با 0.94 است.
مقياسهای اندازهگيری برای ویژگیهای كيفی
همانطور که گفته شد، جامعه آماری و انواع دادههای آن که به صورت کیفی هستند، برای دستهبندی به کار میروند. ولی با توجه به نوع کدگذاری آنها و تبدیلشان به اعداد میتوان دو نوع مقیاس متفاوت برای آنها در نظر گرفت. ۱- «مقیاس اسمی» (Nominal) و ۲- «مقیاس ترتیبی» (Ordinal)

۱- مقیاس اسمی: اگر از کدها و اعداد فقط برای متمایز کردن دادههای کیفی کمک گرفته شود از مقیاس اسمی استفاده شده است. مقدارهای عددی در این حالت قابلیت مرتبسازی اعضا جامعه آماری را نمیدهد.
این کدگذاری میتواند براساس سلیقه یا نظر محقق متفاوت باشد. برای مثال ممکن است فردی برای اسامی شهرهای مربوط به محل تولد که ویژگی کیفی است کدهای عددی در نظر گرفته و مثلاً به شهر تهران کد ۱ و به شهر اصفهان کد ۲ را اختصاص داده باشد، ولی فردی دیگر برای تهران کد ۵ و برای اصفهان کد ۱ را انتخاب کرده باشد.
| نام شهر محل تولد (ویژگی کیفی) | کد گذاری با مقیاس اسمی |
| تهران | ۱ |
| اصفهان | ۲ |
| شیراز | ۳ |
| بیرجند | ۴ |
۲- مقیاس ترتیبی: زمانی که دادههای کیفی را بوسیله اعدادی کد گذاری کنیم که ترتيب این دادهها حفظ شود از مقیاس ترتیبی استفاده کردهایم. مثلاً اگر برای ميزان مهارت که مقدارهای ضعیف، متوسط و زیاد را دارد از کدهای عددی ۱، ۲ و ۳ استفاده کنیم، ترتیب دادههای کیفی را بوسیله کدگذاری حفظ کردهایم. البته ممکن است فرد دیگری کدهای ۰، ۱۰ و ۲۰ را برای میزان مهارت در نظر بگیرد ولی براساس هر دو روش، مهارت ضعیف از مهارت متوسط و زیاد مقدار کمتری دارد.
| میزان مهارت (ویژگی کیفی) | کدگذاری با مقیاس ترتیبی |
| ضعیف | ۱ |
| متوسط | ۲ |
| زیاد | ۳ |
محاسبه شاخصهای تمرکز برای دادههای کیفی و کمی
با توجه به ماهیت متفاوت جامعه آماری و انواع دادههای آن و همچنین مقیاسهای اندازهگیری، جدول زیر وجود بعضی از شاخصهای تمرکز (میانگین، میانه، و نما) را برای هر یک مشخص میکند.
| نوع داده | مقیاس اندازهگیری | میانگین | میانه | نما |
| کیفی | اسمی | --- | --- | |
| ترتیبی | --- | |||
| کمی | فاصلهای | |||
| نسبی |













عالی بود سپاسگزارم
بسیار عالی و گویا بود سپاس از تدریس قابل درک تون
سلام به فرادرس . ممنون برای اموزش های بسیار کارگشا و مفیدتون . خدا خیرتون بده
با سلام و احترام
از اینکه مطالب را بسیار قابل فهم و عالی تدریس میکنید خیلی خیلی ممنونم
امیدوارم همیشه پرتوان و برقرار باشید
بسیار عالی و کاربردی، بسیار سپاسگزارم. در پناه خدا پیروز و پاینده باشید.
بسیار روان و خوب
متشکرم خیلی مفید و عالی است