کار و انرژی پتانسیل — به زبان ساده

اصل کار و انرژی پتانسیل یکی از نظریه‌های مهم در دوره‌های مقدماتی فیزیک است. این موضوع آنقدر مهم است که ممکن است کمی گیج‌کننده به نظر بیاید، ولی در واقع اینگونه نیست. در این مطلب قصد داریم کار و انرژی پتانسیل و رابطه آن‌ها را به زبان ساده و قابل فهم ارائه کنیم.

کار

بسیاری از متن‌های مربوط به کار و انرژی پتانسیل در فیزیک با این جمله شروع می‌شوند که انرژی نه ایجاد می‌شود و نه از بین می‌رود و تنها از شکلی به شکل دیگر تغییر می‌کند. همچنین انواع مختلفی از انرژی وجود دارد که شامل انرژی جنبشی، انرژی پتانسیل، انرژی حرارتی و انرژی شیمیایی می‌شود.

از طرف دیگر کار به عنوان توانایی تغییر انرژی تعریف می‌شود. شاید این موضوع خنده‌دار به نظر بیاید ولی تقریباً تمام کتاب‌هایی که قصد آموزش مفهوم کار و انرژی پتانسیل را دارند از همین طریق بحث را باز می‌کنند و به این ترتیب رابطه ریاضی کار را ارائه می‌دهند که عبارت است از:

$$W=F\Delta r\cos \theta$$

که $$F$$ نیرو، $$\Delta r$$ جابه جایی و $$\theta$$ زاویه بین نیرو و جابه جایی است. قدم بعدی این است که بدانید تفاوت کارها در چیست؟ فرض کنید من یک بلوک را مانند شکل زیر از نقطه $$A$$ تا نقطه $$B$$ حرکت دهم.

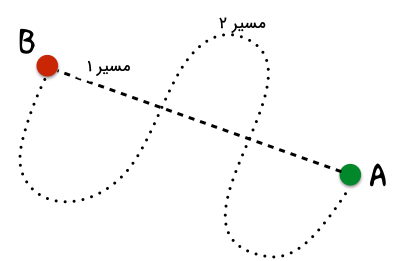
در صورتی که اصطکاک وجود داشته باشد کار دو مسیر با یکدیگر یکسان نیست و کار مسیر ۲ بیشتر از مسیر ۱ است ولی اگر نیروی وارد بر جسم تنها گرانش باشد و کار با نیروی گرانش انجام شود، کار مسیر ۱ و مسیر ۲ با یکدیگر یکسان خواهد بود.

نیروهای پایستار و ناپایستار

تفاوت نیروی گرانش و اصطکاک در چیست که سبب متغیر شدن مقدار کار و انرژی پتانسیل در دو مسیر می‌شود؟ در جواب به این سوال باید گفت که گرانش را یک نیروی پایستار و اصطکاک را یک نیروی ناپایستار می‌نامیم. در حقیقت در نیروی پایستار مسیر حرکت بر میزان کار انجام شده توسط نیرو تاثیر ندارد ولی در نیروی ناپایستار مسیر حرکت در میزان کار و انرژی پتانسیل دستگاه تاثیر دارد. در نیروهای پایستار مانند گرانش، نیروی فنر، نیروهای الکترواستاتیک و غیره کل انرژی جنبشی جسم به کار و انرژی پتانسیل تبدیل می‌شود و در نتیجه داریم:

$$W=\Delta K+\Delta U$$

اما اگر در سیستم نیروهای ناپایستار مانند اصطکاک وجود داشته باشد، تمام انرژی پتانسیل به انرژی جنبشی تبدیل نمی‌شود و بخشی از این انرژی هدر می‌رود و به گرما تبدیل می‌شود. به همین دلیل رابطه کار و انرژی به صورت زیر در می‌آید:

$$W=\Delta K+\Delta U+\Delta E_{th}$$

در رابطه بالا، انرژی گرمایی به دلیل اصطکاک به وجود می‌آید. مشکل یا ویژگی مهم نیروهای ناپایستار این است که برگشت‌پذیر نیستند. یعنی اگر جسمی که از نقطه $$A$$ به نقطه $$B$$ رفته است را در نظر بگیریم و فرض کنیم دوباره به نقطه اولیه خودش روی همان مسیر باز می‌گردد، نمی‌توان انرژی گرمایی را مجدداً به انرژی جنبشی برای حرکت تبدیل کرد و در حقیقت این انرژی به صورت گرما به محیط اطراف یا جسم داده می‌شود.

به همین دلیل است که وقتی به توپی روی زمین ضربه‌ای وارد می‌کنید، مسافتی را طی می‌کند و سپس متوقف می‌شود. در حقیقت اگر نیروی اتلافی وجود نداشته باشد توپ بی‌وقفه با تبدیل انرژی پتانسیل ضربه‌ای که به توپ زدید به انرژی جنبشی باید به حرکتش ادامه می‌داد ولی در حضور نیروهای اتلافی حرکت توپ بعد از مدتی متوقف می‌شود.

انرژی پتانسیل

از نظر فیزیکی انرژی که در جسم ذخیره شود و قابل تبدیل به کار باشد را انرژی پتانسیل می‌گوییم. یک جسم می‌تواند انرژی را در نتیجه مکان و موقعیت خود ذخیره کند. به عنوان مثال توپ سنگین ماشین‌های تخریب ساختمان هنگامی که در موقعیت بالایی در ارتفاع نگه داشته می‌شود انرژی را ذخیره می‌کند. از این انرژی ذخیره شده بر حسب موقعیت جسم به عنوان انرژی پتانسیل یاد می‌شود. به همین ترتیب یک کمان کشیده شده قادر است انرژی را در نتیجه موقعیت خود ذخیره کند. هنگامی که کمان در حالت معمول خود یعنی بدون کشیدگی قرار گیرد، انرژی در کمان ذخیره نمی‌شود. اما هنگامی که موقعیت آن از موقعیت تعادل معمول خود تغییر کند کمان قادر است انرژی را به دلیل موقعیت خود ذخیره کند. از این انرژی ذخیره شده بر حسب موقعیت به عنوان انرژی پتانسیل یاد می‌شود. انرژی پتانسیل انرژی ذخیره شده بر حسب موقعیتی است که توسط یک جسم در اختیار گرفته شده است.

همان طور که گفته شد جنس پتانسیل انرژی است و واحد آن نیز بر حسب ژول بیان می‌شود. انرژی پتانسیل انواع مختلفی دارد مانند انرژی پتانسیل گرانشی، انرژی پتانسیل کشسانی یا انرژی پتانسیل الکتریکی که در ادامه در مورد آن‌ها صحبت خواهیم کرد.

انرژی پتانسیل الکتریکی

انرژی پتانسیل الکتریکی انرژی مورد نیاز برای حرکت یک بار در برابر یک میدان الکتریکی است. برای حرکت بیشتر بار در میدان الکتریکی به انرژی بیشتری نیاز دارید همچنین برای انتقال آن از طریق میدان الکتریکی قوی‌تر نیز به انرژی بیشتری نیاز دارید.

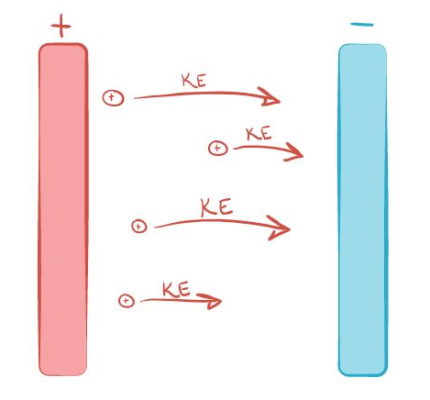
تصور کنید که یک صفحه با بار منفی بسیار زیاد دارید که ذره‌ای دیگر با بار مثبت از طریق نیروی الکتریکی به آن چسبیده است. یک میدان الکتریکی در اطراف صفحه وجود دارد که تمام اشیا دارای بار مثبت را به سمت خود می‌کشد، در حالی که سایر اشیای دارای بار منفی را از خود دور می‌کند.

حالا شما ذره مثبت را برداشته و می‌خواهید در مقابل کشش میدان الکتریکی آن را از صفحه خارج کنید. این کار سخت است زیرا نیروی الکتریکی آن‌ها را به هم نزدیک می‌کند. اگر ذره مثبت را رها کنید ذره دوباره به صفحه منفی برمی‌گردد که توسط نیروی الکتریکی کشیده می‌شود. انرژی که شما برای انتقال ذره از صفحه استفاده کردید به عنوان انرژی پتانسیل الکتریکی در ذره ذخیره می‌شود. این پتانسیلی است که ذره هنگام رها شدن با آن حرکت می‌کند.

هر چه ذره مثبت را از صفحه دورتر کنید باید انرژی بیشتری مصرف کنید. بنابراین انرژی پتانسیل الکتریکی بیشتری در آن ذخیره می‌شود. اگر بار موجود روی صفحه را دو برابر کنیم دوباره به انرژی بیشتری برای حرکت ذره مثبت نیاز خواهید داشت. اگر بار ذره مثبت را دو برابر کنیم ، برای جابه جایی آن به انرژی بیشتری احتیاج دارید. حال فرض کنید که به جای صفحه‌ای با بار منفی صفحه دارای بار مثبت است. ذرات مثبت از صفحه دور می‌شوند زیرا هر دو دارای بار مثبت هستند. این بار باید انرژی بگذاریم تا سعی کنیم ذره را به جای اینکه دور کنیم به صفحه نزدیک کنیم. بدین ترتیب انرژی پتانسیل الکتریکی ذخیره شده در جسم برابر است با:

$$U_{r}=\frac{qQ}{4\pi \epsilon_{0}}\frac{1}{r}$$

که $$U_{r}$$ انرژی پتانسیل الکتریکی ذخیره شده در بار نقطه‌ای $$q$$ زمانی است که از بار $$Q$$ به اندازه $$r$$ فاصله دارد. همچنین اختلاف انرژی پتانسیل الکتریکی دو نقطه $$A$$ و $$B$$ برابر با $$U_{AB}=U_{B}-U_{A}$$ است.

انرژی پتانسیل گرانشی

همان‌طور که گفتیم انرژی پتانسیل انرژی است که به دلیل موقعیت جسم در آن ایجاد می‌شود. انرژی ذخیره شده در یک جسم در نتیجه موقعیت عمودی یا ارتفاع آن باعث ایجاد انرژی پتانسیل گرانشی در جسم می‌شود. این انرژی در نتیجه جاذبه زمین در جسم ذخیره می‌شود. انرژی پتانسیل گرانشی توپ عظیم ماشین‌های تخریب به دو متغیر جرم توپ و ارتفاعی که توپ در آن قرار گرفته وابسته است. بین انرژی پتانسیل گرانشی و جرم یک جسم رابطه مستقیمی وجود دارد و اجرام سنگین‌تر انرژی پتانسیل گرانشی بیشتری دارند. همچنین بین انرژی پتانسیل گرانشی و ارتفاع جسم نیز رابطه مستقیمی وجود دارد. هرچه جسم بالاتر رود مقدار انرژی پتانسیل گرانشی بیشتر است. این روابط با معادله زیر بیان می‌شود:

$$E_{grav}=mass. g . height$$
$$E_{grav}=m. g . h$$

در معادله فوق $$m$$ جرم جسم، $$h$$ ارتفاع جسم و $$g$$ شتاب میدان گرانش است ($$g=9.8 \frac{m}{s^{2}}$$). برای تعیین انرژی پتانسیل گرانشی یک جسم ابتدا باید به طور دلخواه موقعیت ارتفاع صفر تعیین شود که به طور معمول زمین به عنوان موقعیتی از ارتفاع صفر در نظر گرفته می‌شود یا به عنوان مثال از آنجا که بسیاری از آزمایش‌ها روی میز انجام می‌شوند در نظر گرفتن میز به عنوان ارتفاع صفر مرسوم است.

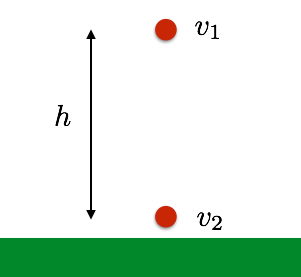
اگر روی یک میز را به عنوان نقطه مرجع یا صفر پتانسیل گرانشی در نظر بگیریم انرژی پتانسیل یک شی بر اساس ارتفاع آن نسبت به میز محاسبه می‌شود. به عنوان مثال یک آونگ که از بالای میز رو به بالا و از بالای آن تاب می‌خورد دارای انرژی پتانسیل است که می‌تواند براساس ارتفاع آن از میز اندازه گیری شود. با اندازه گیری جرم و ارتفاع آونگ در بالای میز می‌توان انرژی پتانسیل آونگ را تعیین کرد.

از آنجا که انرژی پتانسیل گرانشی یک جسم مستقیماً متناسب با ارتفاع آن از موقعیت صفر است دو برابر شدن ارتفاع منجر به دو برابر شدن انرژی پتانسیل گرانش، سه برابر شدن ارتفاع منجر به سه برابر شدن انرژی پتانسیل گرانش و غیره می‌شود.

مثال: با دانستن اینکه انرژی پتانسیل در بالای سکوی بلند $$50$$ ژول است و با استفاده از اصل پایستگی انرژی و وابستگی ارتفاع به پتانسیل گرانشی، جاهای خالی در نمودار زیر را پر کنید.

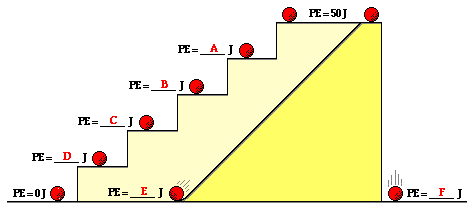
پاسخ: چون پله‌ها ارتفاع یکسانی دارند و از ابتدا تا انتهای مسیر از پنج پله تشکیل شده است. با حرکت به سمت بالا و به ازای هر پله مقدار یکسانی از انرژی پتانسیل در جسم ذخیره می‌شود. در این صورت چون پتانسیل جسم در پایین صفر و در بالای پله‌ها ۵۰ ژول است.

• انرژی پتانسیل در نقطه $$A$$ برابر با ۴۰ ژول است.
• انرژی پتانسیل در نقطه $$B$$ برابر با ۳۰ژول است.
• انرژی پتانسیل در نقطه $$C$$ برابر با 20 ژول است.
• انرژی پتانسیل در نقطه $$D$$ برابر با 10 ژول است.
• همچنین نقاط $$E$$ و $$F$$ چون در ارتفاع یکسانی قرار دارند پس انرژی پتانسیل گرانشی آن‌ها برابر با یکدیگر و ۰ ژول است.

انرژی پتانسیل کشسانی

سومین شکل انرژی پتانسیل که در مورد آن صحبت خواهیم کرد انرژی پتانسیل الاستیک یا کشسانی است. انرژی پتانسیل کشسانی انرژی ذخیره شده در مواد الاستیک در نتیجه کشش یا فشرده‌سازی آن‌ها است. انرژی پتانسیل الاستیک را می‌توان در نوارهای لاستیک، طناب های بانجی‌جامپینگ، ترامپولین، فنر، تیر کشیده شده در کمان و غیره ذخیره کرد. مقدار انرژی پتانسیل الاستیک ذخیره شده در چنین دستگاهی به میزان کشش دستگاه مربوط می‌شود هرچه میزان کشش بیشتر باشد، انرژی ذخیره شده بیشتر است.

فنرها نمونه خاصی از دستگاهی هستند که می‌توانند انرژی پتانسیل الاستیک را به دلیل فشرده‌سازی یا کشش ذخیره کنند. برای فشرده سازی فنر نیرو لازم است. فشرده‌سازی بیشتر نیروی بیشتری را می‌طلبد. برای اکثر فنرها طبق قانون هوک مقدار نیرو مستقیماً با میزان کشش یا فشرده‌سازی فنر متناسب است ($$x$$)، ثابت تناسب بین نیرو و میزان فشردگی یا کشیدگی به عنوان ثابت فنر ($$k$$) شناخته می‌شود و داریم:

$$F=k.x$$

گفته می‌شود که چنین فنرهایی از قانون هوک پیروی می‌کنند. اگر یک فنر کشیده یا فشرده نشود هیچ انرژی پتانسیل الاستیکی در آن ذخیره نشده است و گفته می‌شود که فنر در موقعیت تعادل قرار دارد. موقعیت تعادل به موقعیتی گفته می‌شود که فنر به طور طبیعی وقتی نیرویی به آن وارد نمی‌شود به خود می‌گیرد. از نظر انرژی پتانسیل موقعیت تعادل را می توان موقعیت انرژی پتانسیل صفر نامید. یک معادله ویژه برای فنرها وجود دارد که مقدار انرژی پتانسیل کشسانی را به میزان کشش (یا فشرده سازی) و ثابت فنر مربوط می‌کند و برابر است با:

$$E=\frac{1}{2}kx^{2}$$

به طور خلاصه انرژی پتانسیل انرژی است که به دلیل موقعیت جسم نسبت به موقعیت پتانسیل صفر انتخابی در جسم ذخیره می‌شود. اگر جسمی در ارتفاع بالاتر (یا زیر) ارتفاع صفر قرار گیرد دارای انرژی پتانسیل گرانشی است. اگر جسم در موقعیتی غیر از نقطه تعادل در یک محیط الاستیک قرار گیرد دارای انرژی پتانسیل کشسانی است و با دور یا نزدیک کردن یک ذره باردار به یک میدان الکتریکی در آن انرژی ذخیره می‌شود.

نمودار انرژی پتانسیل

یک جسم را در نظر بگیرید که در صورت عدم وجود مقاومت هوا در نزدیکی سطح زمین به صورت عمودی سقوط می‌کند. انرژی مکانیکی ذخیره شده در جسم برابر با $$E=K+U$$ و انرژی پتانسیل با توجه به سطح صفر که در روی زمین در نظر گرفته می‌شود برابر با $$U(y)=mgy$$ است که یک خط مستقیم از مبداء با شیب $$mg$$ است. در نمودار نشان داده شده در تصویر، محور $$x$$ ارتفاع بالای سطح زمین و محور $$y$$ انرژی جسم است.

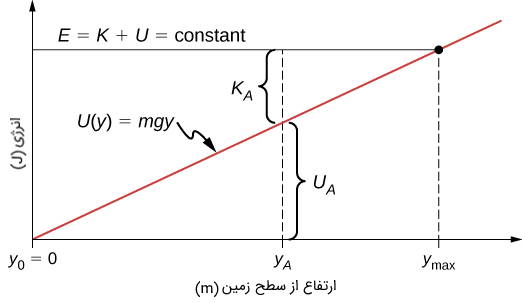
$$E$$ در نمودار نشان‌دهنده انرژی مکانیکی ثابت جسم است در حالی که انرژی‌های جنبشی و پتانسیل $$K_{A}$$ و $$U_{A}$$ در یک ارتفاع خاص $$y_{A}$$ نشان داده شده‌اند. می‌توان دید که با تغییر ارتفاع جسم کل انرژی بین انرژی جنبشی و پتانسیل تبدیل می‌شود. از آنجا که انرژی جنبشی هرگز نمی‌تواند منفی باشد حداکثر انرژی پتانسیل و حداکثر ارتفاعی وجود دارد که جسم نمی‌تواند از این حد عبور کند.

$$K=E-U\geq 0\rightarrow U\leq E$$

اگر نقطه مرجع انرژی پتانسیل گرانشی را در $$y_{0}$$ در نظر بگیریم، با استفاده از رابطه انرژی پتانسیل گرانشی داریم:

$$y\leq \frac{E}{mg}=y_{max}$$

در عبارت بالا نشان دادیم که مقدار کل انرژی تقسیم بر وزن ($$mg$$) در حداکثر ارتفاع ذره یا $$y_{max}$$ قرار دارد. در حداکثر ارتفاع انرژی جنبشی و سرعت صفر هستند بنابراین اگر جسم در ابتدا به سمت بالا حرکت کند سرعت در $$y_{max}$$ صفر می‌شود و این نقطه به عنوان نقطه بازگشت در حرکت است که در آن جهت سرعت تغییر می‌کند. در سطح زمین انرژی پتانسیل صفر و انرژی جنبشی و سرعت حداکثر هستند.

$$U_{0}=0=E-K_{0}$$

$$E=K_{0}=\frac{1}{2}mv_0^2$$

$$v_{0}=\pm \sqrt{\frac{2E}{m}}$$

حداکثر سرعت $$\pm v_{0}$$ سرعت اولیه لازم برای رسیدن به ارتفاع $$y_{max}$$ و  $$-v_{0}$$ نشان دهنده سرعت نهایی پس از سقوط از $$y_{max}$$ است. می‌توان تمام این اطلاعات و موارد دیگر را از نمودار انرژی پتانسیلی که نشان داده‌ایم استخراج کرد.

یک سیستم جرم و فنر را در سطح بدون اصطکاک ثابت و افقی در نظر بگیرید (از گرانش و اصطکاک صرف نظر کنید). این ساختار یک سیستم یک بعدی است که انرژی مکانیکی آن ثابت و برابر با $$E$$ است و انرژی پتانسیل آن $$U=\frac{1}{2}kx^{2}$$ است.

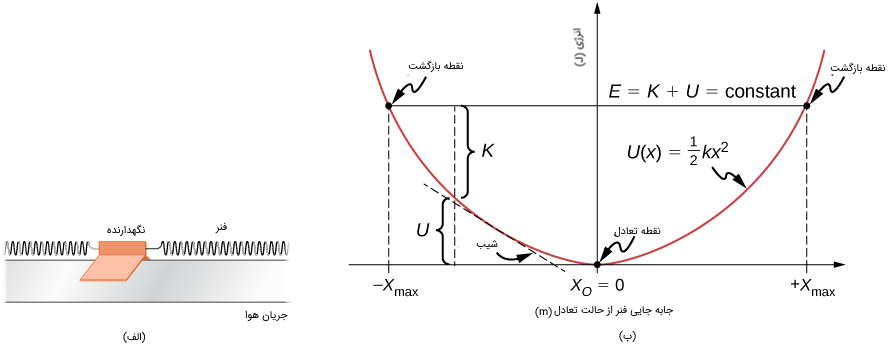
در این حالت نیز می‌توان اطلاعات مربوط به حرکت جسم را همانند حالت سقوط آزاد جسم از نمودار پتانسیل استخراج کرد. همانطور که برای جسم در سقوط آزاد بررسی شد در این حالت نیز می‌توانیم دامنه حرکت مجاز فیزیکی و حداکثر مقادیر فاصله و سرعت را از حدود انرژی جنبشی یعنی $$0\leq K\leq E$$ محاسبه کنیم. بنابراین نقطه‌ای که $$K=0$$ است انرژی مکانیکی کل برابر با انرژی پتانسیل کشسانی است و داریم:

$$U=E\rightarrow \frac{1}{2}kx^{2}=E$$
$$x_{max}=\pm \sqrt{\frac{2E}{k}}$$

حرکت رفت و برگشتی فنر محدود به ناحیه بین نقاط بازگشت یعنی $$-x_{max}\leq x \leq x_{max}$$ است و برای هر مقدار مثبت $$E$$ صادق است. در این حالت به دلیل شکل منحنی انرژی پتانسیل $$U(x)$$ را یک چاه پتانسیل بی نهایت می‌نامند. در قعر چاه پتانسیل یعنی جایی که $$U(x)$$ و $$x$$ صفر هستند و انرژی جنبشی حداکثر است، داریم:

$$K=E\rightarrow v_{max}=\pm \sqrt{\frac{2E}{m}}$$

همچنین از شیب منحنی انرژی پتانسیل می‌توانیم اطلاعات مربوط به نیروی وارد شده روی فنر و شتاب آن را نیز استخراج کنیم. هم‌چنین می‌دانیم که منفی شیب نمودار انرژی پتانسیل برابر با نیرو است یعنی

$$F=-\triangledown U$$

و بنابراین گرادیان نمودار انرژی پتانسیل، متناسب با شتاب است. وقتی $$x=0$$ است شیب، نیرو و شتاب صفر هستند و بنابراین یک نقطه تعادل داریم. منفی شیب در دو طرف نقطه تعادل نیرویی بازگشتی به سمت نقطه تعادل را می‌دهد که برابر است با  $$F=\pm kx$$. بنابراین تعادل پایدار نامیده می‌شود و نیرو را نیروی بازگردانی می‌نامند. این موضوع نشان می‌دهد که $$U(x)$$ در نقطه تعادل دارای کمینه نسبی است. اگر نیرو در دو طرف یک نقطه تعادل جهتی مخالف از جهت تغییر موقعیت داشته باشد تعادل ناپایدار نامیده می‌شود و نشان‌دهنده این است که $$U(x)$$ در آن نقطه ماکزیمم نسبی دارد. برای درک بهتر این موضوع مثالی در این زمینه حل می‌کنیم.

مثال: انرژی پتانسیل برای ذره‌ای که در امتداد محور x حرکت یک بعدی را تجربه می‌کند برابر با $$U(x)=2(x^{4}-x^{2})$$ است که U برحسب ژول و x برحسب متر است. ذره در معرض نیروهای ناپایستار نیست و انرژی مکانیکی آن مقدار ثابت $$E=-0.25\ J$$ را دارد. (الف) آیا حرکت ذره به ناحیه‌ای در محور x محدود می‌شود و اگر چنین است مقدار این مناطق چه قدر است؟ (ب) آیا نقاط تعادلی وجود دارد؟ و اگر چنین است مقدار و نوع تعادل چه قدر است؟

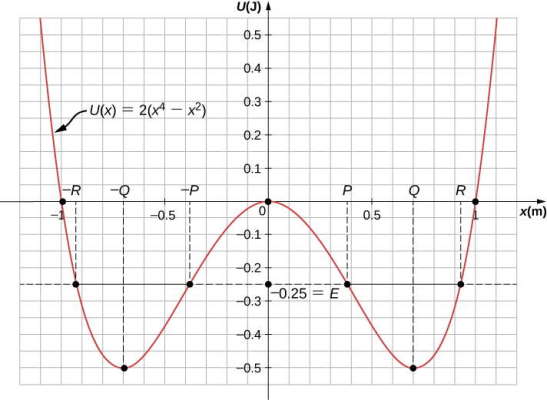
حل: می توان مقادیر مناطق مجاز در امتداد محور x را برای مقدار داده شده انرژی مکانیکی از این شرط که انرژی جنبشی نمی‌تواند منفی باشد پیدا کرد و نقاط تعادل و نوع پایداری آن‌ها از خصوصیات نیرو قابل محاسبه است.

به صورت کلی با نگاه کردن به نمودار می‌توان دید که دو ناحیه مجاز برای حرکت با توجه به شرط ($$E>U$$) و سه‌نقطه تعادل ($$\frac{dU(x)}{dx}=0$$) وجود دارد که یکی از آن‌ها ناپایدار ($$\frac{d^{2}U(x)}{dx^{2}}<0$$) و دو نقطه تعادل دیگر پایدار ($$\frac{d^{2}U(x)}{dx^{2}}>0$$) هستند.

الف) برای پیدا کردن مناطق مجاز حرکت ذره در نمودار انرژی پتانسیل داریم:

$$K=E-U=-0.25-2(x^{4}-x^{2})\geq 0$$

می‌توان معادله بالا را به یک اتحاد کامل تبدیل کرد و داریم:

$$2(x^{2}-\frac{1}{2})^{2}\leq\frac{1}{4}$$

و در نتیجه داریم:

$$\frac{1}{2}-\sqrt{\frac{1}{8}}\leq x^{2} \leq \frac{1}{2}+\sqrt{\frac{1}{8}}$$

بدین ترتیب دو ناحیه مجاز را برای $$x$$ به دست می‌آوریم:

$$-x_{R}\leq x \leq -x_{P}$$

$$x_{P}\leq x \leq x_{R}$$

در رابطه‌های بالا $$x_{P}=0.38$$ و $$x_{R}=0.92$$ است.

ب) برای پیدا کردن نقاط تعادل از معادله پتانسیل نسبت به مکان مشتق می‌گیریم و داریم:

$$\frac{dU}{dx}=8x^{3}-4x=0$$

ریشه‌های معادله بالا برابر با $$x=0,x=\pm \frac{1}{\sqrt{2}}$$ هستند. از معادله بالا یکبار دیگر نسبت به مکان یا $$x$$ مشتق می‌گیریم و داریم:

$$\frac{d^{2}U}{dx^{2}}=24x^{2}-4$$

این معادله در $$x=0$$ منفی است که نشان‌دهنده یک ماکزیمم در نمودار و نقطه تعادل ناپایدار است. در نقطه‌های $$x=\pm \frac{1}{\sqrt{2}}$$ مشتق دوم مثبت است که نشان‌دهنده تعادل پایدار است.

کار و انرژی پتانسیل

در مورد انرژی پتانسیل همه چیز به سیستمی که انتخاب می‌کنید بستگی دارد. اگر می‌خواهید انرژی پتانسیل را محاسبه کنید باید سیستمی در نظر بگیرید که بیش از یک جسم در آن باشد. به عنوان مثال  یک توپ در حالت سکون را در نظر بگیرید که در نزدیکی سطح زمین در ارتفاع $$h$$ قرار گرفته است.

اگر سیستم را طوری انتخاب کنیم که فقط متشکل از توپ باشد می‌توان در هنگام افتادن توپ به کار انجام شده روی این توپ نگاه کرد. چه نیروهایی روی توپ عمل می‌کنند؟ فقط نیروی جاذبه یعنی $$mg$$. از آنجایی که نیروی جاذبه در جهت جابه جایی قرار دارد، زاویه بین نیرو و جابه جایی صفر است و داریم:

$$W=F\Delta r=mgh$$

از طرفی از قضیه کار و انرژی جنبشی می‌دانیم که تغییرات انرژی جنبشی برابر با کار وارد بر سیستم است، یعنی داریم:

$$W=\Delta K=K_{2}-K_{1}$$

و در نتیجه

$$mgh=K_{2}-K_{1}$$

حال اگر سیستم را طوری تغییر دهیم که هم توپ و هم زمین را شامل شود چه نتیجه‌ای حاصل می‌شود؟ در این صورت می‌توان کار انجام شده توسط نیروی گرانش را از هر دو طرف معادله بالا کم کرد و داریم:

$$mgh-W_{g}=\Delta K-W_{g}$$

از نظر جبری این همان معادله قبلی است. با این حال این معادله بیان می‌کند که کار کل سیستم زمین و توپ صفر است و در عوض یک تغییر در انرژی پتانسیل گرانشی ($$U$$) داریم و تغییر انرژی پتانسیل برابر با منفی کار انجام شده توسط نیرو است. این کمیت از نظر فیزیکی انرژی پتانسیل گرانشی سیستم توپ-زمین نام دارد.

بدین ترتیب می‌توان گفت که مهمترین گام در حل مشکلات کار-انرژی انتخاب سیستم است و برای نیروهای داخلی (مانند نیروی جاذبه) در یک سیستم یک کمیت انرژی پتانسیل وجود دارد.

بر همین اساس باید گفت که در سیستمی که نیروی ناپایستار وجود ندارد کار انجام شده روی سیستم برابر با منفی تغییرات انرژی پتانسیل سیستم است و داریم:

$$W=-\Delta U$$

پس می‌توان گفت اگر کار روی سیستمی صفر باشد یعنی انرژی پتانسیلی در آن ذخیره نشده است و در صورت انجام کار روی سیستم، مقدار انرژی پتانسیل ذخیره شده در سیستم منفی کار انجام شده روی سیستم است.