نگاشت موبیوس – از صفر تا صد

یکی از نگاشت‌های ابتدایی توسط آگوست فردینانند موبیوس (Augustus Ferdinand Möbius) مطالعه و بررسی شد. این نگاشت به راحتی با نسبت دو عبارت خطی بیان و معمولاً به عنوان تبدیل خطی کسری یا دوخطی (Bilinear) شناخته می‌شود. در این آموزش، نگاشت موبیوس (Mobius Transformation) را معرفی می‌کنیم و نشان می‌دهیم که چگونه از این نگاشت برای تصویر یک به یک دیسک بر روی نیم‌صفحه استفاده می‌شود. یک ویژگی مهم تبدیل موبیوس، این است که جز در یک نقطه، در کل صفحه مختلط سازگار (Conformal) است.

تبدیل موبیوس

چهار عدد مختلط و ثابت $$a$$، $$b$$، $$c$$ و $$d$$ را در نظر بگیرید که در رابطه $$ad \neq bc$$ صدق می‌کنند. تابع زیر یک تبدیل یا نگاشت دوخطی، یا نگاشت موبیوس یا نگاشت خطی کسری نامیده می‌شود:

$$\large w = S (z) = \dfrac {a z + b} { cz + d} \;\;\;\;\; (1)$$

اگر در معادله (۱) عبارت $$S (z)$$ را در $$c z + d$$ ضرب کنیم، به فرم دوخطی $$cwz - az + d w - b = 0$$ می‌رسیم.

جملات شامل $$z$$ را به یک سمت تساوی می‌آوریم و خواهیم داشت: $$z ( cw -a) = -dw + b$$. در نتیجه، برای مقادیر $$w \neq \frac { a } {c}$$ تبدیل معکوس به صورت زیر خواهد بود:

$$\large z = S ^ {-1} (w) = \dfrac {- d w + b} { c w - a} \;\;\;\;\; (2)$$

می‌توانیم $$S(z)$$ و $$S^{-1}(w)$$ را به نگاشت‌هایی در صفحه مختلط گسترش دهیم.

مقدار $$S ( \infty)$$ برابر با حد $$S (z)$$ است، وقتی که $$z \to \infty$$. بنابراین، داریم:

$$\large S ( \infty ) = \lim _ {z \to \infty } S (z) = \lim _ {z \to \infty} \frac {a + \frac{b}{z}}{c +\frac {d}{z}} = \frac { a } {c}$$

و معکوس آن، برابر با $$S ^{-1} \left ( \frac{a}{c} \right ) = \infty$$. به طور مشابه، مقدار $$S ^ {-1} (\infty)$$ به صورت زیر محاسبه می‌شود:

$$\large S ^ {-1} ( \infty ) = \lim _ {w \to \infty } S ^ {-1} (w) = \lim _ {z \to \infty} \frac {-d + \frac{b}{w}}{c -\frac {a}{w}} = \frac { -d } {c}$$

و معکوس $$S ^ {-1} \left ( \frac {-d} { c} \right ) = \infty$$ را خواهیم داشت. با این عبارات، می‌توانیم نتیجه بگیریم که نگاشت $$w = S ( z )$$ یک نگاشت یک به یک از صفحه مختلط $$z$$ به صفحه مختلط $$w$$ است.

اکنون نشان خواهیم داد که یک نگاشت موبیوس، دسته‌ای از دایره‌ها و خطوط را به خودشان می‌نگارد. اگر $$S (z)$$ یک نگاشت موبیوس دلخواه مطابق رابطه (۱) باشد و $$c = 0$$، آنگاه $$S (z)$$ به یک نگاشت خطی کاهش می‌یابد که خط را به خط و دایره را به دایره تصویر می‌کند. اگر $$c \neq 0$$، آنگاه می‌توانیم $$S (z)$$ را به فرم زیر بنویسیم:

$$\large \begin{align*} S ( z ) & = \frac { az + b } {c z + d } = \frac { c (az + b) } { c ( c z + d ) } = \frac {acz + bc } {c (c z + d)} \\ & = \frac {acz + ad - ad + bc} {c (cz + d)} \\ & = \frac {a (cz + d) - ad + bc} {c (cz + d)} \\ & = \frac {a} {c } + \frac {bc - ad} {c} \frac {1} { cz + d } \end {align*} \;\;\;\;\; (3)$$

شرط $$ad \neq bc$$ از این موضوع جلوگیری می‌کند که $$S (z)$$ به یک ثابت ختم شود. معادله (۳) نشان می‌دهد که $$S (z)$$ را می‌توان به عنوان ترکیبی از توابع در نظر گرفت. عبارت $$\xi = c z + d$$ یک تبدیل خطی است. همچنین $$Z = \frac { 1 } { \xi}$$ یک تبدیل وارون است. در نتیجه، رابطه (۳) به صورت $$w = \frac { a } {c} + \frac{bc-ad}{c}Z$$ در می‌آید.

یک نیم‌صفحه را می‌توان به عنوان دسته‌ای از خطوط موازی و یک دیسک را به عنوان دسته‌ای از دایره‌ها در نظر گرفت.

مثال ۱

نشان دهید $$w = S (z) = \frac {i (1-z)}{1 + z }$$ دیسک واحد $$D : \; |z|<1$$ را به صورت یک به یک به نیم‌صفحه بالایی $$\text{Im}(z) > 0$$ می‌نگارد.

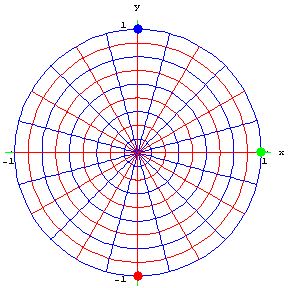
حل: ابتدا دایره واحد $$C : \;\; |z|= 1$$ را در نظر می‌گیریم که مرز دیسک را تشکیل می‌دهد و تصویر آن را در صفحه $$w$$ به دست می‌دهد.

اگر $$S ( z ) = \frac { - i z + i } { z + 1 }$$ را بنویسیم، خواهیم دید که $$a = - i$$، $$b = i$$ و $$d = 1$$.

با استفاده از معادله (۲) نگاشت معکوس را به دست می‌آوریم:

$$\large z = S ^ {-1} (w) = \frac { - d w + b} { c w - a } = \frac { - (1) w + (i)} {(1) w - (- i )} = \frac { - w + i } {w + i } . \;\;\;\;\; (4)$$

اگر $$|z| = 1$$، آنگاه معادله (۴) منجر به این می‌شود که نگاشت نقاط روی دایره واحد در رابطه $$\left | \frac { - w + i } { w+ i} \right | = 1$$ صدق کنند که معادله زیر را نتیجه می‌دهد:

$$\large | w + i | = | - w + i | \;\;\;\;\; (5)$$

با در نظر گرفتن $$w = u + i v$$ و به توان دو رساندن دو سمت معادله (۵)، خواهیم داشت:

$$\large | u + i v + i | = | - u - i v + i| \\ \large |u + i (1+ v ) | ^ 2 = | -u + i (1- v)| ^ 2 \\ \large u ^ 2 + (1 + v ) ^ 2 = (-u ) ^ 2 + ( 1- v ) ^ 2 \\ \large u ^ 2 + ( 1 + v ) ^ 2 = u ^ 2 +(1-v ) ^ 2 \\ \large (1+v)^ 2 = (1 - v ) ^ 2 \\ \large 1 + 2 v + v ^ 2 = 1 - 2 v + v ^ 2 \\ \large v = 0$$

که معادله محور $$u$$ در صفحه $$w$$ است.

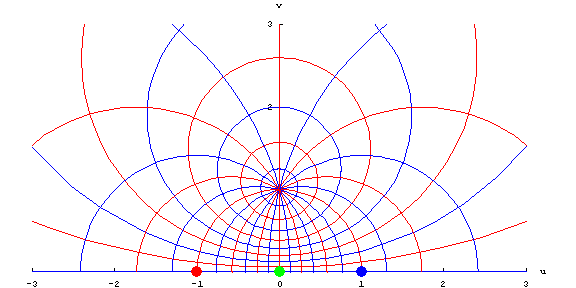
دایره $$C$$ صفحه $$z$$ را به دو بخش تقسیم می‌کند و تصویر یا نگاشت آن، محور $$u$$ است که صفحه $$w$$ را به دو بخش تقسیم می‌کند. تصویر نقطه $$z = 0$$، نقطه $$w = S(0) = i$$ است، بنابراین، انتظار داریم درون دایره $$C$$ به بخشی از صفحه $$w$$ تصویر شود که بالای محور $$u$$ قرار دارد. برای نشان دادن صحت این گفته، $$|z|<1$$ را در نظر می‌گیریم. بنابراین، معادله (۴) نتیجه می‌دهد که مقادیر نگاشت باید در نامعادله $$| - w + i | < |w + i |$$ صدق کنند که آن را به صورت زیر در نظر می‌گیریم:

$$\large d _ 1 = | w - i | < | w - (-i)| = d _ 2 .$$

اگر $$d _ 1$$ را به عنوان فاصله از $$w$$ تا $$i$$، و $$d _ 2$$ را فاصله $$- w$$ تا $$i$$ در نظر بگیریم، آنگاه، استدلال هندسی نشان می‌دهد که نقطه تصویر $$w$$ باید در نیم‌صفحه بالایی $$\text{Im} > 0$$ صدق کند (شکل ۳).

$$|z| < 1$$ تحت نگاشت $$w = \frac { i ( 1 - z ) } { 1 + z }$$، نقاط $$z _ 1 = - i$$، $$z _ 2 = 1$$ و $$z _ 3 = i$$ را به ترتیب، به نقاط $$w _ 1 = -1$$، $$w _ 2 = 0$$ و $$w _ 3 = 1$$ می‌نگارد." width="640" height="272">

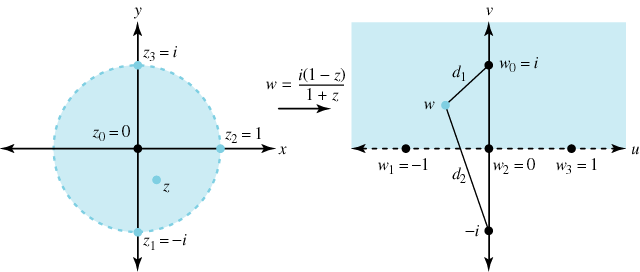
فرمول ضمنی نگاشت موبیوس

فرمول عمومی برای یک نگاشت دوخطی (معادله (۱)) بر اساس چهار ضریب وابسته $$a$$، $$b$$، $$c$$ و $$d$$ ظاهر می‌شود. اما، از آنجایی که $$S (z)$$ ثابت نیست ($$a \neq 0$$ یا $$c \neq 0$$)، می‌توانیم نگاشت را با سه ضریب مجهول توضیح دهیم و به ترتیب، به صورت زیر بنویسیم:

$$\large S (z) = \frac {z + \frac {b}{a}} {\frac{c}{a} z + \frac {d}{a} }$$   یا   $$\large S (z) = \frac {\frac { a}{c} z+ \frac {b }{c}} {z + \frac {d }{c} }$$

فیلم آموزش ریاضی مهندسی – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

بنابراین، اگر مقدار سه نقطه مجزای $$S (z _ 1 ) = w _ 1$$، $$S (z_2) = w _ 2$$ و $$S (z_ 3 ) = w _ 3$$ مشخص باشند، می‌توانیم یک تبدیل خطی منحصر به فرد را تعیین کنیم. برای تعیین چنین نگاشتی، می‌توانیم به سادگی از فرمول ضمنی که در آن $$z$$ و $$w$$ حضور دارند، استفاده کنیم.

قضیه ۱ (فرمول ضمنی): یک نگاشت موبیوس منحصر به فرد وجود دارد که مقادیر سه نقطه تصویر مجزای $$z _ 1$$، $$z _ 2$$ و $$z _ 3$$ را به ترتیب به نقاط مجزای $$w _ 1$$، $$w _ 2$$ و $$w _ 3$$ تصویر می‌کند. یک فرمول ضمنی برای این نگاشت با معادله زیر بیان می‌شود:

$$\large \frac{(z - z _ 1) (z _ 2 - z _ 3 )} {(z - z _ 3 ) (z _ 2 - z _1)} = \frac {(w - w _1) (w _ 2 - w _ 3)} { ( w - w _3 ) ( w _ 2 - w _ 1 ) } \; \; \; \; \; ( 6 )$$

مثال ۲

نگاشت موبیوس $$w = S (z )$$ را به دست آورید که نقاط $$z _ 1 = - i$$، $$z _ 2 = 1$$ و $$z _ 3 = i$$ را به ترتیب، به نقاط $$w _ 1 = -1$$، $$w _ 2 = 0$$ و $$w _ 3 = 1$$ می‌نگارد.

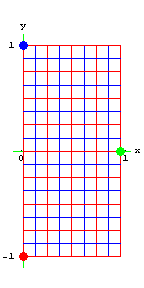
حل: از فرمول ضمنی رابطه (۶) استفاده می‌کنیم:

$$\large \frac{(z - (-i)) (z _ 2 - i )} {(z - i ) (1 - (-i) ) } = \frac {(w - (-1)) (0 - 1 ) } { ( w - 1 ) ( 0 - (-1) ) } \\ \large \frac {(z + i ) ( 1 - i) }{(z - i ) ( 1+ i ) } = \frac { (w + 1 ) ( 0 - 1 ) } { ( w - 1 ) (0 + 1 ) } \\ \large \frac {(z + i ) ( 1 - i ) } { ( z - i ) ( 1 + i ) } = \frac { w + 1 } { - w + 1 }$$

با گسترش این رابطه و جمع کردن جملات مشابه $$w$$ و $$z w$$ در سمت چپ و ساده‌سازی، آن‌ها، خواهیم داشت:

$$\large ( z - i ) ( 1 + i ) ( w + 1 ) = ( z + i ) ( 1 - i ) ( - w + 1 ) \\ \large ( 1 + i ) z w + ( 1 - i ) w + ( 1 + i ) z + ( 1 - i ) = ( - 1 + i ) z w + ( -1 - i ) w + ( 1 - i ) z + ( 1 + i ) \\ \large z w + i z w + w - i w + z + i z + 1 - i = -z w + i z w - w - i w + z - i z + 1 + i \\ \large 2 zw + 2 w = - 2 i z + 2 i \\ \large zw + w = - i z + i \\ \large w ( 1 + z ) = i ( 1 - z )$$

بنابراین، نگاشت موبیوس مورد نظر، به صورت زیر خواهد بود:

$$\large w = S ( z ) = \frac { i ( 1 - z ) } { 1 + z }$$

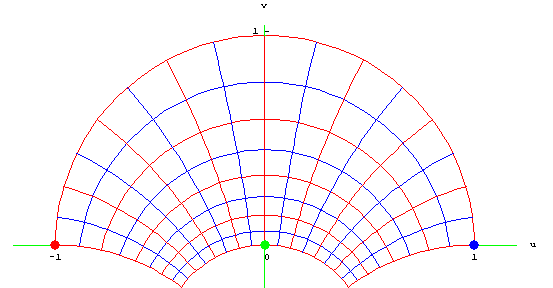
مثال ۳

نگاشت دوخطی $$w = S ( z )$$ را بیابید که نقاطه $$z _ 1 = -2$$، $$z _ 2 = -1-i$$ و $$z _ 3 = 0$$ را به ترتیب، به نقاط $$w _ 1 = -1$$، $$w _ 2 = 0$$ و $$w _ 3 = 1$$ می‌نگارد.

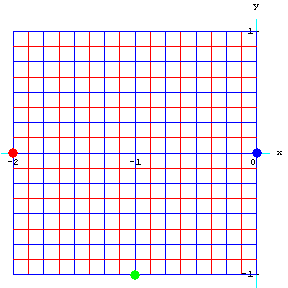
حل: از معادله ضمنی (۶)‌ استفاده می‌کنیم:

$$\large \begin {align*} \frac { (z - ( - 2 ) ) \left ( \left ( - 1 - i \right ) - 0 \right ) } { ( z - 0 ) \left ( \left ( - 1 - i \right ) - ( - 2 ) \right ) } & = \frac { ( w - ( - 1 ) ) ( 0 - 1 ) } { ( w - 1 ) ( 0 - ( - 1 ) ) } \\ \frac { ( z + 2 ) \left ( - 1 - i \right ) } { ( z ) \left ( - 1 - i + 2 \right ) } & = \frac { ( w + 1 ) ( - 1 ) } { ( w - 1 ) ( 1 ) } \\ \frac { z + 2 } { z } \frac { - 1 - i } { 1 - i } & = \frac { 1 + w } { 1 - w } \end {align*}$$

با استفاده از این حقیقت که $$\frac { - 1 - i } { 1 - i } = \frac { 1 } { i }$$، معادله را به صورت زیر بازنویسی می‌کنیم:

$$\large \frac { z + 2 } { i z } = \frac { 1 + w } { 1 - w } .$$

اکنون معادله را گسترش می‌دهیم:

$$\large \begin {aligned} ( z + 2 ) ( 1 - w) & = i z ( 1 + w ) \\ z + 2 - z w - 2 w & = iz + iz w \\ z - iz + 2 & = z w + iz w + 2 w \\ \left ( 1 - i \right ) z + 2 & = w \left ( z + i z + 2 \right ) \\ \left ( 1 - i \right ) z + 2 & = w \left ( \left ( 1 + i \right ) z + 2 \right ) \end {aligned}$$

که می‌توان آن را بر حسب $$z$$ به صورت زیر نوشت:

$$\large w = S ( z ) = \frac { ( 1 - i ) z + 2 } { (1+ i ) z + 2 }$$

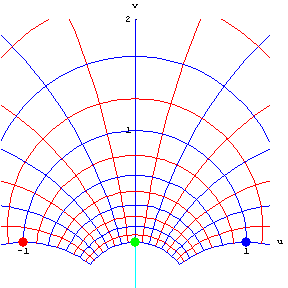
فرض کنید $$D$$ ناحیه‌ای در صفحه $$z$$ باشد که با یک دایره یا خط راست $$C$$ محدود شده است. همچنین، فرض کنید $$z _1$$، $$z _ 2$$ و $$z _ 3$$ سه نقطه مجزا باشند که روی $$C$$ قرار داشته و دارای این ویژگی باشند که یک ناظر متحرک در طول $$C$$ از $$z _ 1$$ تا $$z _ 2$$ و از آنجا تا $$z _ 3$$ حرکت کند، ناحیه $$D$$ را بیابد. اگر $$C$$ یک دایره و $$D$$ درون $$C$$ باشد، آنگاه می‌توان گفت که $$C$$ در جهت مثبت چرخیده است. در مقابل، سه نقطه $$(z _ 1, z _ 2 , z _ 3 )$$ به طور منحصر به فرد، ناحیه‌ای را تعیین می‌کنند که در سمت چپ $$C$$ صدق می‌کند.

$$G$$ را ناحیه‌ای در صفحه $$w$$ در نظر می‌گیریم که با دایره یا خط راست $$K$$ محدود شده است. همچنین، فرض می‌کنیم $$w _1$$، $$w _ 2$$ و $$w_ 3$$ سه نقطه مجزا باشند که روی $$K$$ قرار گرفته‌اند، به طوری که یک ناظر متحرک در طول $$K$$ از $$w _ 1$$ تا $$w _ 3$$ که از $$w _ 2$$ می‌گذرد، ناحیه $$G$$ را پیدا می‌کند که باید در سمت چپ باشد. از آنجایی که نگاشت موبیوس یک نگاشت سازگار است که دسته‌ای از دایره‌ها و خطوط راست را به خودشان می‌نگارد، می‌توانیم از فرمول ضمنی برای تشکیل $$w = S ( z )$$ استفاده کنیم که یک نگاشت یک به یک از $$D$$ به $$G$$ است.

مثال ۴

نشان دهید نگاشت $$w = S ( z ) = \frac { (1-i)z + 2 } { ( 1 + i ) z + 2 }$$ دیسک $$D : \;\; |z+1|<1$$ را به صورت یک به یک به نیم‌صفحه $$\text{Im} ( w) > 0$$ می‌نگارد.

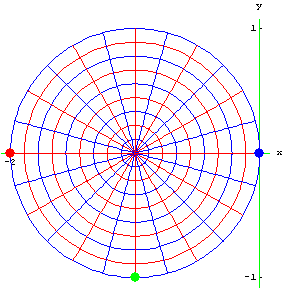
حل: برای سادگی، سه نقطه $$z _ 1 = -2$$، $$z _ 2 = -1-i$$ و $$z _ 3 = 0$$ را در نظر می‌گیریم که دایره $$C: \;\; |z+1| = 1$$ را مشخص می‌کنند که یک چرخش مثبت دارد و دیسک $$D$$ دارای یک چرخش به چپ است. تصاویر متناظر با این نقاط به صورت زیر هستند:

$$\large w _ 1 = S ( z _ 1) = S (-2) = -1$$

$$\large w _ 2 = S (z_ 2 ) = S ( -1 -i ) = 0$$

$$\large w _ 3 = S (z _ 3) = S ( 0) = 1$$

از آنجایی که سه نقطه $$w _ 1 = -1$$، $$w _ 2 = 0$$ و $$w _ 3 = 1$$ روی محور $$u$$ قرار دارند، تصویر دایره $$C$$ محور $$u$$ است. نقاط $$w _ 1 = -1$$، $$w _ 2 = 0$$ و $$w _ 3 = 1$$ نیم‌صفحه بالایی $$G : \;\; \text{Im} (w) > 0$$ یک چرخش چپ را نشان می‌دهد. بنابراین، $$w = S ( z ) = \frac {(1-i) z + 2 } {(1+i) z + 2 }$$ دیسک $$D$$ را به نیم‌صفحه بالایی $$G$$ نگاشت می‌دهد.

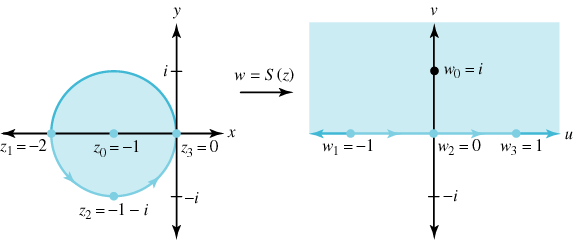
برای بررسی، نقطه $$z _ 0$$ را انتخاب می‌کنیم که در $$D$$ صدق کند و نیم‌صفحه‌ای را پیدا می‌کنیم که تصویر $$w _ 0$$ در آن صدق کند. انتخاب $$z_ 0 = -1$$ نقطه $$w _ 0 = S (z_0) = i$$ را نتیجه خواهد داد. بنابراین، نیم‌صفحه بالایی تصویر صحیح است. این موضوع در شکل زیر نشان داده شده است.

$$w = S ( z ) = \frac { (1-i)z + 2 } { ( 1 + i ) z + 2 }$$" width="573" height="240">

قضیه (فرمول ضمنی با با یک نقطه در بی‌نهایت): در معادله (۶) می‌توان نقطه‌ای در بی‌نهایت در صفحه $$z$$ یا صفحه $$w$$ در نظر گرفت.

اثبات:

حالت ۱: اگر $$z _ 3 = \infty$$، آنگاه می‌توانیم $$\frac { ( z _ 2 - z _ 3 ) } { ( z - z _ 3 ) } = \frac { ( z _ 2 - \infty ) } { (z - \infty )} = 1$$ را بنویسیم و آن را در معادله (۶) قرار دهیم:

$$\large \frac { ( z – z _ 1 ) ( z _ 2 – \infty ) } { ( z – \infty ) ( z _ 2 – z _ 1 ) } = \frac { ( w – w _ 1 ) ( w _ 2 – w _ 3 ) }{ ( w – w_ 3 ) (w_ 2 – w_ 1 )}$$

این رابطه را می‌توان به صورت زیر بازنویسی کرد:

$$\large \frac { ( z – z _ 1 ) ( z _ 2 – \infty ) } { ( z – \infty ) ( z _ 2 – z _ 1 ) } = \frac { ( w – w _ 1 ) ( w _ 2 – w_ 3 ) }{ (w_ 2 – w_ 1 ) ( w – w_ 3 ) }$$

و در نهایت، خواهیم داشت:

$$\large \frac { z - z _ 1 }{ z_ 2 - z_ 1 } = \frac { ( w -w _ 1 ) ( w _ 2 - w _ 3 ) } { ( w - w _ 3 ) ( w _ 2 - w _ 1 ) }$$

حالت ۲: اگر $$w _ 3 = \infty$$، آنگاه می‌توانیم $$\frac { ( w _ 2 - w _ 3 ) } { ( w - w _ 3 ) } = \frac { ( w _ 2 - \infty ) } { (w - \infty )} = 1$$ را بنویسیم و آن را در معادله (۶) قرار دهیم:

$$\large \frac { ( z - z _ 1 ) ( z _ 2 - z _ 3 ) } { ( z - z _ 3 ) ( z _ 2 - z _ 1 ) } = \frac { ( w - w _ 1 ) ( w _ 2 - \infty ) }{ ( w - \infty ) (w_ 2 - w_ 1 )}$$

این رابطه را می‌توان به صورت زیر بازنویسی کرد:

$$\large \frac { ( z - z _ 1 ) ( z _ 2 - z _ 3 ) } { ( z - z _ 3 ) ( z _ 2 - z _ 1 ) } = \frac { ( w - w _ 1 ) ( w _ 2 - \infty ) }{ (w_ 2 - w_ 1 ) ( w - \infty ) }$$

و در نهایت، خواهیم داشت:

$$\large \frac { ( z - z _ 1 ) ( z _ 2 - z _ 3 ) } { ( z - z _ 3 ) ( z _ 2 - z _ 1 ) } = \frac { w - w _ 1 }{ w_ 2 - w_ 1 } \;\;\;\;\; (7)$$

گاهی، معادله (۷) برای نگاشت یک ناحیه هلالی شکل استفاده می‌شود که دوایر مماس را به نوار بی‌کران می‌نگارد.

مثال ۵

تبدیل موبیوس $$w = S (z)$$ را پیدا کنید که ناحیه هلالی شکل درون دیسک $$D : \;\; |z-2|<2$$ و بیرون دایره‌ $$|z-1| = 1$$ را به یک نوار افقی می‌نگارد.

حل: برای سادگی، نقاط $$z _ 1 = 4$$، $$z _ 2 = 2 + 2 i$$ و $$z _ 3 = 0$$ و مقادیر تصویر آن‌ها، یعنی به ترتیب، $$w _ 1 = 0$$، $$w _ 2 = 1$$ و $$w _ 3 = \infty$$ را انتخاب می‌کنیم. سه‌تایی مرتب $$z _ 1 = -4$$، $$z _ 2 = 2+2 i$$ و $$z _ 3 = 0$$ دایره $$C: \;\; |z- 2 | = 2$$ با چرخش مثبت و دیسک $$D : \;\; |z - 2 | < 2$$ با چرخش منفی را نشان می‌دهند. نقاط تصویر $$w _ 1 = 0$$، $$w _ 2 = 1$$ و $$w _ 3 = \infty$$ همه در محور $$u$$ صدق کرده و یک چرخش منفی را برای نیم‌صفحه بالایی $$\text{Im} (w) > 0$$ مشخص می‌کنند. بنابراین، می‌توانیم از فرمول ضمنی دوم (معادله (۷)) استفاده کنیم:

$$\large \frac { ( z - 4 ) ( 2 + 2 i - 0 ) } { ( z - 0 ) ( 2 + 2 i - 4 ) } = \frac {w - 0 } { 1 - 0 },$$

که نگاشت دیسک $$D : \;\; |z-2|< 2$$ را به نیم‌صفحه بالایی $$\text{Im} ( w ) > 0$$ را مشخص می‌کند. با توجه به اینکه $$\frac {2+2 i } {-2+2i } = - io$$، خواهیم داشت:

$$\large \frac {z-4}{z} \frac {2 + 2 i } {-2+2 i } = \frac {z-4} { z } ( - i ) = \frac {w } { 1 }$$

که می‌توان آن را به فرم زیر نوشت:

$$\large w = S (z) = \frac { - i z + i 4 } { z } .$$

با استفاده از محاسبات سرراست، می‌توان نشان داد که نقاط $$z _ 4 = 1 - i$$، $$z _ 5 = 2$$ و $$z _ 6 = 1 + i$$ به نقاط زیر تصویر می‌شوند:

$$\large w _ 4 = S (z _ 4 ) = S ( 1 - i ) = -2 + i \\ \large w 5 = S ( z _ 5 ) = S ( 2 ) = i \\ \large w _ 6 = S (z _ 6 ) = S ( 1 + i ) = 2 + i$$

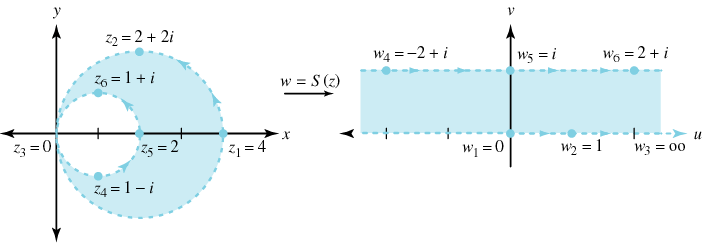
نقاط $$w _ 4 = - 2 + i$$، $$w _ 5 = i$$ و $$w _ 6 = 2 + i$$ در خط افقی $$\text{Im} (w) > 1$$ در نیم‌صفحه بالایی صدق می‌کنند. بنابراین، همان‌گونه که در شکل زیر نشان داده شده است، ناحیه هلالی شکل به نوار افقی $$0 < \text{Im} (w) < 1$$ تصویر می‌شود.

$$w = S (z) = \frac { – i z + i 4 } { z }$$" width="702" height="243">

اگر این مطلب برای شما مفید بوده است، آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس ریاضیات
• آموزش ریاضیات مهندسی
• مجموعه آموزش‌های ریاضیات و فیزیک پایه
• آموزش ریاضیات مهندسی (مرور – تست کنکور ارشد)
• فراکتال چیست؟ — به زبان ساده
• توان و ریشه اعداد مختلط — از صفر تا صد
• فرم نمایی و قطبی اعداد مختلط — به زبان ساده

^^