ممان اینرسی دایره – به زبان ساده + فرمول و محاسبه
ممان اینرسی یا گشتاور دوم سطح دایره، کمیتی است که نحوه توزیع نقاط مختلف این شکل را نسبت به یک محور مشخص نمایش میدهد. این کمیت، به منظور ارزیابی خواص مقاومتی اجسام دارای مقطع دایرهای نظیر شفتها مورد استفاده قرار میگیرد. به عنوان مثال، هرچه ممان اینرسی یک قطعه با مقطع دایرهای، بزرگتر باشد، مقاومت آن در برابر خمش بیشتر خواهد بود. گشتاور دوم سطح دایره، یک مشخصه هندسی است و تنها به شکل سطح بستگی دارد. در این مقاله، به تعریف ممان اینرسی دایره و مقایسه آن با ممان اینرسی شکلهای مرتبط میپردازیم. علاوه بر این، ضمن معرفی فرمولهای ممان اینرسی سطح، چند مثال متنوع را نیز تشریح میکنیم.
ممان اینرسی سطح چیست ؟
«ممان اینرسی سطح» (Area Moment of Inertia) یا «گشتاور دوم سطح» (Second Moment of Area)، یک مشخصه هندسی است که توزیع نقاط یک مقطع دوبعدی نسبت محورهای مورد نظر را به صورت کمی نمایش میدهد. به عنوان مثال، دو مقطع با مساحت و جنس یکسان را در نظر بگیرید.
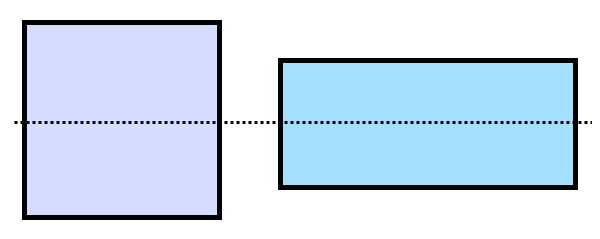
تصویر بالا، یک مقطع مربعی و یک مقطع مستطیلی با مساحتهای برابر را نمایش میدهد. خطچین نمایش داده شده، محور افقی گذرنده از مرکز این دو مقطع است. با وجود برابر بودن مساحتها، نحوه توزیع نقاط مقطعها نسبت به این محور، یکسان نیست. نقاط مقطع مستطیلی، مجموعا در فاصله نزدیکتری نسبت به محور قرار دارند. این مسئله، بر روی رفتار مقطع در برابر بارهای خمشی تاثیر میگذارد.
اگر ضلع مربع برابر با ۶ واحد و طول و عرض مستطیل به ترتیب برابر با ۹ و ۴ واحد باشد، ممان اینرسی مستطیل برابر با ۴۸ واحد طول به توان چهار و ممان اینرسی مربع برابر با ۱۰۸ واحد طول به توان چهار خواهد بود. این مقادیر، امکان اظهار نظر راجع به مقاومت خمشی مقطع مستطیلی و مربعی را فراهم میکند. بر این اساس، در صورت اعمال بار در راستای عمود بر محور افقی، مقطع مستطیلی مقاومت کمتری را از خود به نمایش میگذارد و بیشتر تحت خمش قرار میگیرد. رابطه کلی ممان اینرسی مقطع دوبعدی به صورت زیر نوشته میشود:
$$ I _ x = \int \int _ { A } { y ^ ۲ dA } $$
$$
I _ x = \int \int _ { A } { y ^ ۲ d x d y }
$$
$$ I _ y = \int \int _ { A } { x ^ ۲ dA } $$
$$
I _ y = \int \int _ { A } { x ^ ۲ d x d y }
$$
- Ix: گشتاور دوم سطح دایرهای نسبت به محور مرکزی x
- y: فاصله عمودی نقاط تا محور مرکزی x
- Iy: گشتاور دوم سطح دایرهای نسبت به محور مرکزی y
- x: فاصله عمودی نقاط تا محور مرکزی y
- A: مساحت سطح
- dA: مقدار دیفرانسیلی مساحت سطح
در بخشهای بعدی، فرمول ممان اینرسی دایره را با استفاده از این رابطه اثبات خواهیم کرد.
ممان اینرسی دایره چگونه بدست می آید ؟
یک دایره توپر به شعاع R و قطر D را در دستگاه محورهای مختصات دوبعدی x-y در نظر بگیرید. مرکز این دایره بر روی مرکز مختصات منطبق است. محورهای x و y نیز از روی این مرکز عبور میکنند. به عبارت دیگر، محورهای x و y، محورهای مرکزی هستند.
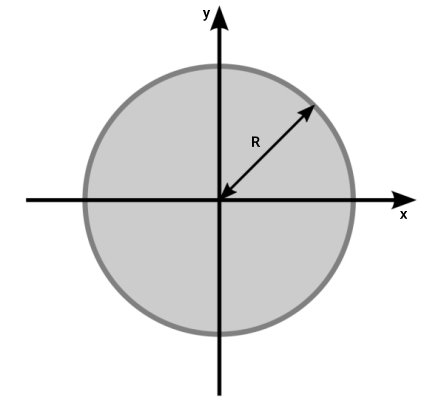
اگر محور مرکزی x را به عنوان محور مبنای محاسبات انتخاب کنیم، ممان اینرسی دایره توپر، از رابطه زیر به دست میآید:
$$
I _ x = \frac { \pi }{ ۴ } R ^ ۴
$$
در صورت انتخاب محور مرکزی y به عنوان محور مبنای محاسبات، فرمول ممان اینرسی دایره به شکل زیر درمیآید:
$$
I _ y = \frac { \pi }{ ۴ } R ^ ۴
$$
- Ix: گشتاور دوم سطح دایرهای نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح دایرهای نسبت به محور مرکزی y
- R: شعاع سطح مقطع دایرهای
به دلیل رابطه بین شعاع و قطر دایره، میتوانیم فرمول ممان اینرسی دایره توپر را بر حسب قطر نیز بنویسیم:
$$
I _ x = \frac { \pi }{ ۶۴ } D ^ ۴
$$
$$
I _ y = \frac { \pi }{ ۶۴ } D ^ ۴
$$
- Ix: گشتاور دوم سطح دایرهای نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح دایرهای نسبت به محور مرکزی y
- D: قطر سطح مقطع دایرهای
همانطور که مشاهده میکنید، فرمولهای ممان اینرسی دایره نسبت به محور x و y با یکدیگر تفاوتی ندارند. دلیل این موضوع، تقارن محوری و تقارن مرکزی شکل دایره است. در شکلهای نامتقارن، این دو فرمول با یکدیگر متفاوت خواهند بود. ممان اینرسی سطح دایره در جهت سوم (راستای محور z) نیز محاسبه میشود که به آن ممان اینرسی قطبی میگویند. در بخشهای بعدی به معرفی این کمیت و کاربردهای آن خواهیم پرداخت.
علامت اختصاری یکای ممان اینرسی سطح دایره چیست ؟
یکای گشتاور دوم سطح دایره در سیستم SI، معمولا به صورت زیر است:
- میلیمتر به توان چهار (mm۴)
- سانتیمتر به توان چهار (cm۴)
- متر به توان چهار (m۴)
در سیستم یکاهای آمریکایی، گشتاور دوم سطح دایره، معمولا بر حسب واحدهای زیر بیان میشود:
- اینچ به توان چهار (in۴)
- فوت به توان چهار (ft۴)
به طور کلی، ممان اینرسی تمام مقاطع از جمله دایره، با یکای طول به توان ۴ بیان میشود. با نگاه کردن به فرمول ممان اینرسی شکلهای مختلف میتوانید به دلیل این موضوع پی ببرید. گشتاور دوم سطح، معمولا با حرف انگلیسی I نمایش داده میشود. اندیس این حرف، بیانگر محور مبنای محاسبات است. به عنوان مثال، Ix، گشتاور دوم سطح نسبت به محور مرکزی x را نمایش میدهد. البته در برخی موارد، گشتاور دوم سطح را با دو اندیس (مانند Ixx یا Iyy) نشان میدهند.
کاربرد ممان اینرسی دایره چیست ؟
ممان اینرسی سطح و کمیتهای مرتبط با آن نظیر ممان اینرسی قطبی، دو مورد از مهمترین مشخصات هندسی مورد استفاده در تحلیل تیر هستند. ممان اینرسی سطح، در ارزیابی قطعات تحت خمش و ممان اینرسی قطبی، در بررسی المانهای دایرهای تحت پیچش (شفتها) کاربرد دارد. این تحلیلها، از اهمیت بالایی در مسائل مهندسی نظیر انتقال نیرو، بارگذاری سازه و غیره برخوردار هستند. میلگرد، یکی از مصالح مهم و پرکاربرد در اجرای سازههای بتنآرمه است که وظیفه افزایش مقاومت کششی و خمشی بتن را بر عهده دارد. در جدول مشخصات میلگرد، معمولا ممان اینرسی آن تحت محور x و y بیان میشود.

میل کاردان خودرو، به منظور انتقال نیرو به چرخها مورد استفاده قرار میگیرد. انتقال نیرو از توربینها به ژنراتورهای الکتریکی نیز به همین شکل انجام میشود. در این موارد و بسیاری از مسائل مشابه، مهندسان باید تنشها و تغییر شکلهای احتمالی را محاسبه کنند تا هیچ شکست مکانیکی در قطعات رخ ندهد. دانستن یا به دست آوردن ممان اینرسی قطعات دارای مقطع دایرهای، برای انجام این محاسبات ضروری است.
مثال ۱: محاسبه ممان اینرسی میلگرد
اگر قطر یک میلگرد برابر با ۵۰ میلیمتر باشد، ممان اینرسی سطح مقطع آن چقدر خواهد بود؟ (عدد پی را برابر با ۳/۱۴ در نظر بگیرید.)
میلگرد، قطعهای با مقطع دایرهای است. برای محاسبه ممان اینرسی مقطعهای دایرهای، از فرمولهای زیر استفاده میکنیم:
$$
I _ x = \frac { \pi }{ ۴ } R ^ ۴
$$
$$
I _ y = \frac { \pi }{ ۴ } R ^ ۴
$$
- Ix: گشتاور دوم سطح دایرهای نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح دایرهای نسبت به محور مرکزی y
- R: شعاع سطح مقطع دایرهای برابر با نصف قطر (۲۵ میلیمتر)
مقادیر معلوم را درون روابط بالا قرار میدهیم:
$$
I _ x = \frac { ۳/۱۴ }{ ۴ } \times ۲۵ ^ ۴
$$
$$
I _ x = \frac { ۳/۱۴ }{ ۴ } \times ۳۹۰۶۲۵
$$
$$ I _ x = \frac { ۱۲۲۶۵۶۲/۵ }{ ۴ } $$
$$
I _ x \approx ۳۰۶۶۴۰
$$
ممان اینرسی مقطع میلگرد حول محور x، تقریبا برابر با ۳۰۶۶۴۰ میلیمتر به توان چهار است.
اثبات ممان اینرسی دایره
به منظور اثبات فرمول ممان اینرسی دایره، ابتدا باید یک دستگاه مختصات مناسب را انتخاب کنیم. برای سطوح دایرهای، دستگاه مختصات قطبی، بهترین گزینه است. به این ترتیب، یک سطح دایرهای را بر روی دستگاه مختصات قطبی، به مرکزیت O و محور قطبی L را در نظر میگیریم. فرض میکنیم مرکز مختصات بر روی مرکز دایره و محور قطبی بر روی محور دوران x قرار دارد (تصویر زیر).
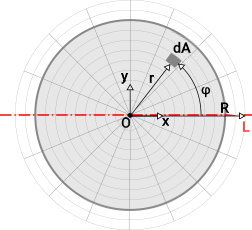
فاصله هر نقطه از دایره تا مرکز مختصات، برابر با r و زاویه بین محور قطبی و هر نقطه، برابر با φ است. φ، در جهت پادساعتگرد اندازهگیری میشود. بر اساس این سیستم، مساحت دیفرانسیلی دایره (dA)، از رابطه زیر به دست میآید:
$$
d A = d r d s = d r ( r d \phi ) = r d r d \phi
$$
- dA: مساحت دیفرانسیلی دایره
- dr: فاصله دیفرانسیلی هر جز تا مرکز مختصات
- ds: طول دیفرانسیلی کمان حاصل از زاویه تفاضلی
- r: فاصله هر جز تا مرکز مختصات
- dφ: زاویه دیفرانسیلی بین محور قطبی و هر جز
برای دایره بسته، بازههای انتگرالگیری به صورت زیر خواهد بود:
$$
r \in [ ۰ \, R ]
$$
$$
\phi \in [ ۰ \, ۲ \pi ]
$$
به عبارت دیگر، فاصله هر جز تا مرکز مختصات، در محدوده ۰ تا R (شعاع دایره) و زاویه بین محور قطبی و هر جز، در محدوده ۰ تا ۲π (۰ تا ۱۸۰ درجه) قرار دارد. علاوه بر این، میتوان مختصات y در هر نقطه را به صورت قطبی و بر حسب r و φ بیان کرد. به این منظور، نقطه فرضی P را در نظر بگیرید.
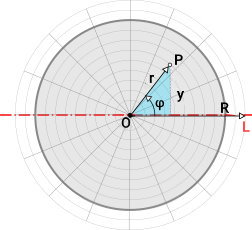
از نقطه P، یک خط تا مرکز مختصات و یک خط عمود بر محور قطبی رسم میکنیم. این خطها به ترتیب r و y نام دارند. زاویه بین محور قطبی و خط r را نیز با φ نمایش میدهیم. به این ترتیب، یک مثلث قائمالزاویه به وجود میآید. r، وتر این مثلث قائمالزاویه است. بر اساس فرمولهای نسبت های مثلثاتی، سینوس زاویه φ، برابر با نسبت طول ضلع مقابل به آن زاویه (y) بر وتر (r) است. بنابراین داریم:
$$
\sin \phi = \frac { y }{ r }
$$
در نتیجه:
$$
y = r \sin \phi
$$
بر اساس فرمول کلی ممان اینرسی سطح داریم:
$$ I _ x = \int \int _ { A } { y ^ ۲ dA } $$
بر اساس روابط قبلی میدانیم:
$$
d A = r d r d \phi
$$
$$
y = r \sin \phi
$$
$$
r \in [ ۰ \, R ]
$$
$$
\phi \in [ ۰ \, ۲ \pi ]
$$
با استفاده از این اطلاعات، انتگرال دوگانه بالا را بازنویسی میکنیم:
$$
I _ x = \int _ {۰} ^ {R} \int _ { ۰ } ^ { ۲ \pi } { r ^ ۲ \sin ^ ۲ \phi \space r \space d \phi d r }
$$
ابتدا بر حسب متغیر φ انتگرال میگیریم:
$$
I _ x = \int _ { ۰ } ^ { R } \left( \int _ { ۰ } ^ { ۲ \pi } r ^ ۳ \sin ^ ۲ \phi \space d \phi \right ) d r
$$
عبارت r۳، در انتگرال اول (داخل پرانتز) به عنوان یک مقدار ثابت در نظر گرفته میشود. بنابراین میتوانیم آن را به پشت انتگرال اول انتقال میدهیم:
$$
I _ x = \int _ { ۰ } ^ { R } \left( r ^ ۳ \int _ { ۰ } ^ { ۲ \pi } \sin ^ ۲ \phi \space d \phi \right ) d r
$$
برای حل راحتتر انتگرال درون پرانتز، عبارت سینوسی را مطابق با رابطه مثلثاتی زیر ساده میکنیم:
$$
\sin ^ ۲ \phi = \frac { ۱ - \cos { ۲ \phi }}{ ۲ }
$$
اکنون این عبارت را درون انتگرال قرار میدهیم و آن را حل میکنیم:
$$
\int _ { ۰ } ^ { ۲ \pi } \sin ^ ۲ \phi \space d \phi = \int _ { ۰ } ^ { ۲ \pi } \frac { ۱ - \cos { ۲ \phi }}{ ۲ } \space d \phi
$$
$$
\int _ { ۰ } ^ { ۲ \pi } \frac { ۱ - \cos { ۲ \phi }}{ ۲ } \space d \phi = \int _ { ۰ } ^ { ۲ \pi } \left( \frac { ۱ }{ ۲ } -frac { \cos { ۲ \phi } }{۲} \space \right) d \phi
$$
$$
\left[ \frac { ۱ }{ ۲ } \phi \right] _ { ۰ } ^ { ۲ \pi } - \left[ \frac { ۱ }{ ۴ } \sin { ۲ \phi } \right] _ { ۰ } ^ { ۲ \pi }
$$
$$
\left( \frac { ۲ \pi }{ ۲ } - ۰ \right) - \left( \frac { ۱ }{ ۴ } \sin { ۴ \phi } - \frac { ۱ }{ ۴ } \sin { ۰ } \right)
$$
$$
\pi - ( ۰ - ۰ ) = \pi
$$
جواب انتگرال اول در بازه ۰ تا ۲π برابر با π شد. اکنون، به سراغ انتگرال دوم میرویم:
$$
I _ x = \int _ { ۰ } ^ { R } \left( r ^ ۳ \pi \right ) d r
$$
π یک عدد ثابت است که میتوان آن را به پشت انتگرال منتقل کرد:
$$
I _ x = \pi \int _ { ۰ } ^ { R } r ^ ۳ d r
$$
با انتگرالگیری از عبارت داخل انتگرال، به رابطه زیر میرسیم:
$$
I _ x = \pi \left[ \frac { r ^ ۴ }{ ۴ } \right ] _ { ۰ } ^ { R }
$$
$$
I _ x = \pi \left ( \frac { R ^ ۴ }{ ۴ } - ۰ \right )
$$
$$
I _ x = \frac { \pi R ^ ۴ }{ ۴ }
$$
در نهایت، به فرمول ممان اینرسی دایره میرسیم.
ممان اینرسی حلقه چگونه بدست می آید ؟
حلقه، یک شکل دوبعدی توخالی است. اگر درون یک دایره توپر، حفرهای دایرهای شکل ایجاد کنیم، یک حلقه به وجود میآید. فاصله بین محیط حفره با محیط بیرونی حلقه، به اندازهای بزرگ است که نمیتوان آن را نادیده گرفت. بنابراین، حلقه با مقطع جدار نازک تفاوت دارد. یک سطح حلقهای شکل با شعاع داخلی R۱، شعاع خارجی R۲، قطر داخلی D۱ و قطر خارجی D۲ را در نظر بگیرید.
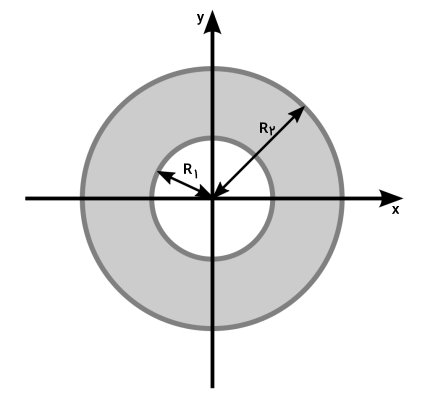
دایره بالا بر روی دستگاه مختصات دوبعدی x-y قرار دارد. مرکز دایره و مرکز مختصات بر روی یکدیگر منطبق هستند. محورهای x و y، نیز از مرکز عبور میکنند. ممان اینرسی سطح این حلقه با استفاده از فرمولهای زیر به دست میآید:
$$
I _ x = \frac { \pi }{ ۴ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$
$$
I _ y = \frac { \pi }{ ۴ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$
- Ix: گشتاور دوم سطح حلقه دایرهای نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح حلقه دایرهای نسبت به محور مرکزی y
- R۱: شعاع داخلی سطح حلقه
- R۲: شعاع خارجی سطح حلقه
فرمولهای ممان اینرسی سطح حلقه بر حسب قطر عبارت هستند از:
$$
I _ x = \frac { \pi }{ ۶۴ } \left ( D _ ۲ ^ ۴ - D _ ۱ ^ ۴ \right )
$$
$$
I _ y = \frac { \pi }{ ۶۴ } \left ( D _ ۲ ^ ۴ - D _ ۱ ^ ۴ \right )
$$
- Ix: گشتاور دوم مقطع جدار نازک دایرهای نسبت به محور مرکزی x
- Iy: گشتاور دوم مقطع جدار نازک دایرهای نسبت به محور مرکزی y
- D۱: قطر داخلی مقطع جدار نازک
- D۲: قطر خارجی سطح حلقه
اثبات فرمول ممان اینرسی سطح حلقه
اثبات فرمول ممان اینرسی سطح حلقه، تفاوت چندانی با اثبات فرمول ممان اینرسی دایره توپر ندارد. تنها تفاوت اصلی در اینجا، بازه انتگرالگیری r است. برای شروع، ابتدا فرمول کلی ممان اینرسی را مینویسیم:
$$ I _ x = \int \int _ { A } { y ^ ۲ dA } $$
میدانیم که:
$$
d A = r d r d \phi
$$
$$
y = r \sin \phi
$$
$$
r \in [ R _ ۱ \, R _ ۲ ]
$$
$$
\phi \in [ ۰ \, ۲ \pi ]
$$
همانطور که مشاهده میکنید، بازه انتگرالگیری نسبت به متغیر r، از R۱ (شعاع داخلی) تا R۲ (شعاع خارجی) است. بنابراین، تا قبل از انتگرالگیری بر حسب r، مراحل اثبات، مشابه مراحل اثبات فرمول ممان اینرسی دایره توپر خواهد بود. به این ترتیب، داریم:
$$
I _ x = \pi \int _ { R _ ۱ } ^ { R _ ۲ } r ^ ۳ d r
$$
$$
I _ x = \pi \left[ \frac { r ^ ۴ }{ ۴ } \right ] _ { R _ ۱ } ^ { R _ ۲ }
$$
$$
I _ x = \pi \left ( \frac { R _ ۲ ^ ۴ }{ ۴ } - \frac { R _ ۱ ^ ۴ }{ ۴ } \right )
$$
$$
I _ x = \frac { \pi } { ۴ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$
مثال ۲: مقایسه ممان اینرسی دایره توپر و حلقه
گشتاور دوم سطح دایرهای به شعاع ۲۰ سانتیمتر را به دست بیاورید. اگر درون این دایره، حفرهای به شعاع ۱۵ سانتیمتر ایجاد کنیم، ممان اینرسی مقطع جدید چه تغییر میکند؟ (عدد پی را برابر با ۳/۱۴ در نظر بگیرید.)
گشتاور دوم سطح دایره توپر، با استفاده از رابطه زیر محاسبه میشود:
$$
I _ c = \frac { \pi }{ ۴ } R ^ ۴
$$
- Ic: گشتاور دوم سطح دایره نسبت به محور مرکزی x یا y
- R: شعاع سطح مقطع دایره برابر با ۲۰ سانتیمتر
$$
I = \frac { \pi }{ ۴ } \times ۲۰ ^ ۴
$$
$$
I = \frac { ۳/۱۴ \times ۱۶۰۰۰۰ }{ ۴ }
$$
$$
I = \frac { ۵۰۲۴۰۰ }{ ۴ }
$$
$$
I = ۱۲۵۶۰۰
$$
به این ترتیب، ممان اینرسی دایره توپر برابر با $$ ۱۲۵۶۰۰ cm ^ ۴ $$ میشود. با ایجاد حفره در دایره، یک حلقه به وجود میآید. شعاع داخلی این حلقه برابر با ۱۵ سانتیمتر (شعاع ) و شعاع خارجی آن برابر با ۲۰ سانتیمتر (شعاع دایره توپر) است. ممان اینرسی این حلقه عبارت است از:
$$
I _ a = \frac { \pi }{ ۴ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$
- Ia: گشتاور دوم سطح دایره نسبت به محور مرکزی x یا y
- R۱: شعاع داخلی حلقه برابر با ۱۵ سانتیمتر
- R۲: شعاع خارجی حلقه برابر با ۲۰ سانتیمتر
$$
I _ a = \frac { \pi }{ ۴ } \left ( ۲۰ ^ ۴ - ۱۵ ^ ۴ \right )
$$
$$
I _ a = \frac { \pi }{ ۴ } \left ( ۱۶۰۰۰۰ - ۵۰۶۲۵ \right )
$$
$$
I _ a = \frac { \pi }{ ۴ } \left ( ۱۰۹۳۷۵ \right )
$$
$$
I _ a = \frac { ۳/۱۴ \times ۱۰۹۳۷۵}{ ۴ }
$$
$$
I _ a = \frac { ۳۴۳۴۳۷/۵ }{ ۴ }
$$
$$
I _ a \approx ۸۵۸۵۹
$$
بنابراین، ممان اینرسی حلقه، تقریبا برابر با $$ ۸۵۸۵۹ cm ^ ۴ $$ است. برای مقایسه ممان اینرسی دایره توپر و حلقه، داریم:
$$
I _ c - I _ a \approx ۱۲۵۶۰۰ - ۸۵۸۵۹ \approx ۳۹۷۴۱
$$
$$
\frac { I _ a }{ I _ c } \approx \frac { ۸۵۸۵۹ }{ ۱۲۵۶۰۰ } \approx ۰/۶۸
$$
به عبارت دیگر، با ایجاد حفره درون دایره، ممان اینرسی سطح جدید به اندازه ۳۹۷۴۱cm۴ کاهش مییابد و به حدود ۶۸ درصد مقدار ممان اینرسی دایره توپر میرسد. اگر شعاع حفره را برابر با ۱۰ در نظر میگرفتیم، ممان اینرسی حلقه به حدود ۹۴ درصد ممان اینرسی دایره توپر میرسید. طراحان از این ویژگی برای کاهش وزن المانها در کنار حفظ درصد زیادی از ممان اینرسی استفاده میکنند. به این ترتیب میتوان قطعهای با مقاومت خمشی خوب و وزن مناسب طراحی کرد.
ممان اینرسی قطبی دایره چیست ؟
«ممان اینرسی قطبی» (Polar Moment of Inertia)، کمیتی است که مقاومت یک تیر یا شفت در برابر پیچش را بر اساس شکل ظاهری مقطع آن نمایش میدهد. به عنوان مثال، سیستم انتقال نیروی زیر را در نظر بگیرید. سطح مقطع شفت در این سیستم، به شکل دایره توپر است. شکل دایره، بیشترین مقاومت را در برابر پیچش از خود به نمایش میگذارد. بنابراین، اغلب مقاطع تحت پیچش، با مقطع دایره توپر یا حلقه ساخته میشوند.

ممان اینرسی قطبی، معمولا با حرف انگلیسی J نمایش داده میشود. یکای این کمیت، طول به توان است و با یکای ممان اینرسی سطح تفاوتی ندارد. فرمول ممان اینرسی قطبی عبارت است از:
$$
J = I _ z = \int _ A r ^ ۲ d A
$$
- J: ممان اینرسی قطبی
- Iz: گشتاور دوم سطح نسبت به محور z
- r: فاصله هر جز تا محور z
- dA: مساحت دیفرانسیلی
برای یک دایره توپر، داریم:
$$
d A = ۲ \pi r dr
$$
- dA: مساحت دیفرانسیلی دایره
- r: فاصله هر نقطه تا محور z
- dr: فاصله دیفرانسیلی هر نقطه تا محور z
اگر محور z از مرکز دایره عبور کند، بازه تغییرات dr از ۰ تا R (شعاع دایره) خواهد بود. به زبان ریاضی:
$$
r \in [ ۰ \, R ]
$$
با استفاده از این اطلاعات، فرمول ممان اینرسی قطبی را برای دایره توپر مینویسیم:
$$
J = I _ z = \int _ ۰ ^ R r ^ ۲ . ۲ \pi r d r
$$
$$
J = I _ z = \int _ ۰ ^ R ۲ \pi r ^ ۳ d r
$$
عبارت ۲π از انتگرال بیرون میآید:
$$
J = I _ z = ۲ \pi \int _ ۰ ^ R r ^ ۳ d r
$$
$$
J = I _ z = ۲ \pi \left [ \frac { r ^ ۴ } { ۴ }\right ] _ ۰ ^ R
$$
$$
J = I _ z = ۲ \pi \left ( \frac { R ^ ۴ } { ۴ } - ۰ \right )
$$
$$
J = I _ z = \pi \frac { R ^ ۴ } { ۲ }
$$
$$
J = I _ z = \frac { \pi } { ۲ } R ^ ۴
$$
- J: ممان اینرسی قطبی
- Iz: گشتاور دوم سطح نسبت به محور مرکزی z
- R: شعاع دایره
به این ترتیب، فرمول ممان اینرسی قطبی حلقه دایرهای عبارت است از:
$$
J = I _ z = \frac { \pi } { ۲ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right )
$$
- J: ممان اینرسی قطبی
- Iz: گشتاور دوم سطح نسبت به محور مرکزی z
- R۱: شعاع داخلی حلقه
- R۲: شعاع خارجی حلقه
کمیت های وابسته به ممان اینرسی قطبی
ممان اینرسی قطبی، معمولا به منظور محاسبه جابجایی زاویهای اشیا تحت پیچش (در راستای موازی با سطح مقطع) مورد استفاده قرار میگیرد. فرمول تغییر شکل زاویهای عبارت است از:
$$
\theta = \frac { T L }{ J G }
$$
- θ: جابجایی زاویهای
- T: پیچش اعمال شده
- L: طول شفت
- J: ممان اینرسی قطبی
- G: مدول برشی
به این ترتیب، برای شفت با مقطع دایرهای، رابطه تغییر شکل زاویهای به صورت زیر نوشته میشود:
$$ \frac { L T }{ G J } $$
- θ: تغییر شکل زاویهای شفت بر حسب رادیان
- L: طول شفت بر حسب میلیمتر
- T: پیچش بر حسب نیوتون-میلیمتر
- G: مدول صلبیت یا مدول برشی بر حسب مگاپاسکال
- J: ممان اینرسی قطبی بر حسب میلیمتر به توان چهار
ممان اینرسی قطبی، در تعیین تنش پیچشی نیز کاربرد دارد. این تنش با استفاده از فرمول زیر به دست میآید:
$$
\tau = \frac { T d }{ J _ z }
$$
- τ: تنش پیچشی
- T: پیچش
- d: فاصله از محور مرکزی
- Jz: ممان اینرسی قطبی
فرمول تنش پیچشی برای شفت با مقطع دایرهای به صورت زیر نوشته میشود:
$$
\tau = \frac { ۲ T d }{ \pi \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right ) }
$$
در شفتهای دایرهای، تنش برشی در سطح شفت به حداکثر مقدار خود میرسد. همانطور که مشاهده میکنید، مفهوم گشتاور دوم سطح یا ممان اینرسی دایره، کاربرد بسیار گستردهای در محاسبه دیگر پارامترهای مهندسی دارد.
قضیه محورهای موازی در ممان اینرسی سطح دایره
در بخشهای قبلی، نحوه محاسبه ممان اینرسی سطح دایره نسبت به محورهای گذرنده از مرکز هندسی این شکل را آموزش دادیم. در این بخش، فرمول محاسبه ممان اینرسی دایره حول محورهای موازی با محورهای مرکزی را معرفی میکنیم. به این منظور، تصویر زیر را در نظر بگیرید.
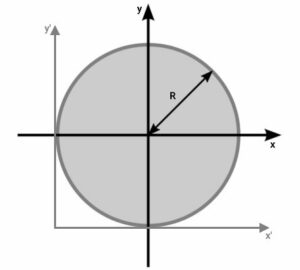
تصویر بالا، دایرهای به شعاع R را در دستگاه مختصات دوبعدی x-y نمایش میدهد. محورهای x و y، از مرکز هندسی دایره عبور میکنند. محورهای 'x و 'y نیز به ترتیب با محور x و y موازی هستند. همانطور که میدانید، ممان اینرسی دایره نسبت محورهای مرکزی از روابط زیر به دست میآید:
$$
I _ x = \frac { \pi }{ ۴ } R ^ ۴
$$
$$
I _ y = \frac { \pi }{ ۴ } R ^ ۴
$$
- Ix: گشتاور دوم سطح دایرهای نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح دایرهای نسبت به محور مرکزی y
- R: شعاع سطح مقطع دایرهای
بر اساس «قضیه محورهای موازی» (Parallel Axes Theorem)، اگر محور 'x، موازی با محور مرکزی x باشد، ممان اینرسی حول 'x، از جمع ممان اینرسی حول x با حاصلضرب مساحت مقطع در فاصله بین دو محور 'x و x محاسبه میشود. بنابراین، فرمول ممان اینرسی دایره بر اساس قضیه محورهای موازی عبارت است از:
$$
I ' = I + A d ^ ۲
$$
- 'I: ممان اینرسی سطح نسبت به محور موازی با محور مرکزی
- I: ممان اینرسی سطح نسبت به محور مرکزی
- A: مساحت شکل
- d: فاصله بین محور موازی مورد نظر با محور مرکزی
برای مقطع دایرهای شکل به شعاع R داریم:
$$ A = \pi R ^ ۲ $$
$$ I = \frac { \pi } { ۴ } R ^ ۴ $$
بنابراین فرمول ممان اینرسی دایره حول محورهای 'x و 'y به صورت زیر نوشته میشود:
$$
I _ { x ' } = \frac { \pi }{ ۴ } R ^ ۴ + \pi R ^ ۲d
$$
$$
I _ { y ' } = \frac { \pi }{ ۴ } R ^ ۴ + \pi R ^ ۲d
$$
- $$ I _ { x ' } $$: گشتاور دوم سطح دایرهای نسبت به محور 'x (موازی با محور مرکزی x)
- $$ I _ { y ' } $$: گشتاور دوم سطح دایرهای نسبت به محور 'y (موازی با محور مرکزی y)
- R: شعاع سطح مقطع دایرهای
- d: فاصله بین محور 'x تا x یا 'y تا y
اگر محور 'x، مماس بر دایره باشد، ممان اینرسی نسبت به 'x از رابطه زیر به دست میآید:
$$
I _ { x ^ { ' } } = I _ x + A d ^ ۲
$$
فاصله محور مرکزی تا محور موازی مورد نظر، برابر با شعاع دایره است:
$$ d = R $$
به این ترتیب، داریم:
$$
I _ { x ^ { ' } } = \frac { \pi } { ۴ } R ^ ۴ + \pi R ^ ۲ R ^ ۲
$$
$$
I _ { x ^ { ' } } = \frac { \pi R ^ ۴ + ۴ \pi R ^ ۴ } { ۴ }
$$
$$
I _ { x ^ { ' } } = \frac { ۵ \pi R ^ ۴ } { ۴ }
$$
- 'Ix: ممان اینرسی سطح نسبت به محور موازی با محور مرکزی x
- R: شعاع دایره
اگر این رابطه را بر رابطه کلی ممان اینرسی تقسیم کنیم، خواهیم داشت:
$$
\frac { I _ { x ^ { ' } } } { I _ x } = \frac { \frac { ۵ \pi R ^ ۴ } { ۴ } } { \frac { \pi R ^ ۴ } { ۴ } } = ۵
$$
همانطور که مشاهده میکنید، در صورت جابجایی محور مبنای ممان اینرسی از مرکز دایره به شعاع آن، مقدار گشتاور دوم سطح، پنج برابر میشود. فاصله دو محور در قضیه محورهای موازی، دارای توان ۲ است. از اینرو، هر این فاصله افزایش یابد، ممان اینرسی به میزان بسیار بیشتری افزایش مییابد.
قضیه محورهای موازی در حلقه دایره ای
برای حلقه دایرهای، اگر محور مبنای ممان اینرسی، موازی با محور مرکزی x و مماس بر سطح بیرونی باشد، قضیه محورهای موازی به صورت زیر نوشته میشود:
$$
I _ { x ^ { ' } } = I _ x + A d ^ ۲
$$
$$
I _ { x ^ { ' } } = \frac { \pi }{ ۴ } \left ( R _ ۲ ^ ۴ - R _ ۱ ^ ۴ \right ) + \pi ( R ^ ۲ _ ۲ - R ^ ۲ _ ۱ ) R ^ ۲ _ ۲
$$
- 'Ix: ممان اینرسی سطح نسبت به محور موازی با محور مرکزی x
- R۱: شعاع داخلی حلقه
- R۲: شعاع خارجی حلقه
ممان اینرسی سطح قطاع دایره
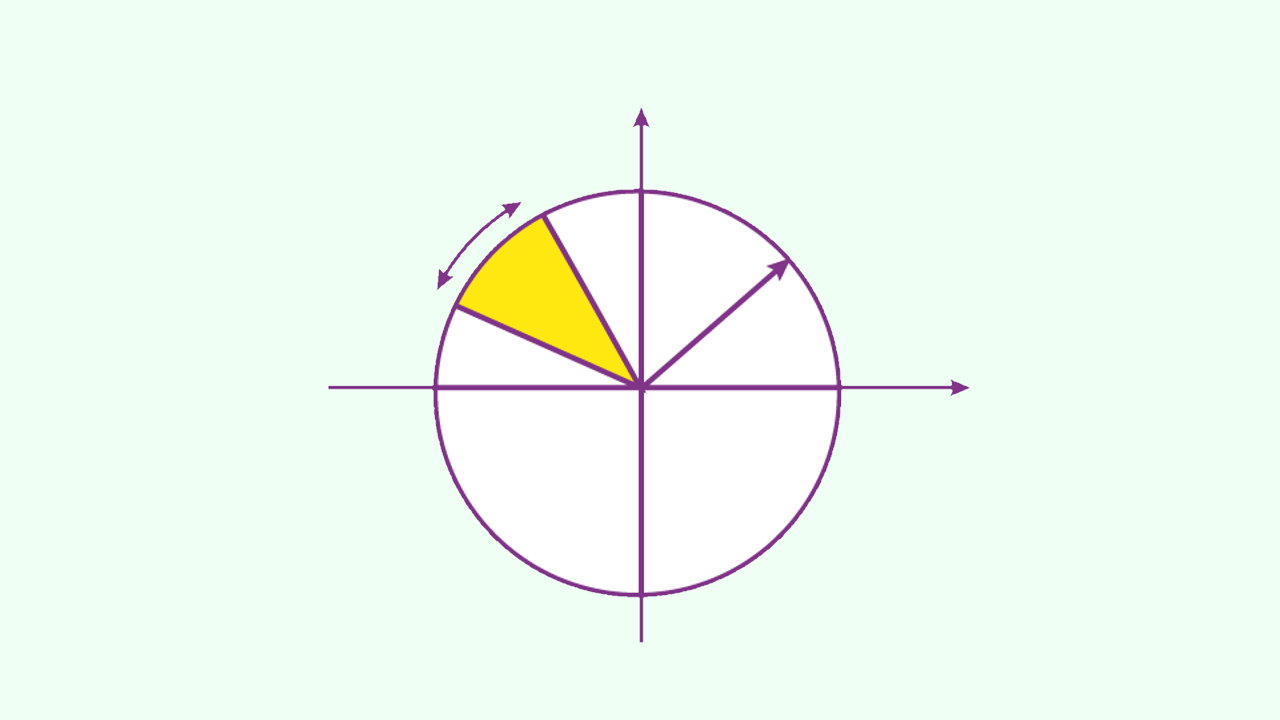
قطاع، بخشی از دایره است که از دو شعاع و یک کمان تشکیل میشود. نیمدایره و ربعدایره، از قطاعهای شناخته شده دایره هستند. ممان اینرسی سطح قطاع، به زاویه روبهروی کمان، شعاع و محور مبنا بستگی دارد. به عنوان مثال، قطاع نمایش داده شده در تصویر زیر را در نظر بگیرد. در این قطاع، شعاع برابر با r و زاویه مقابل به کمان برابر با ۲θ است.
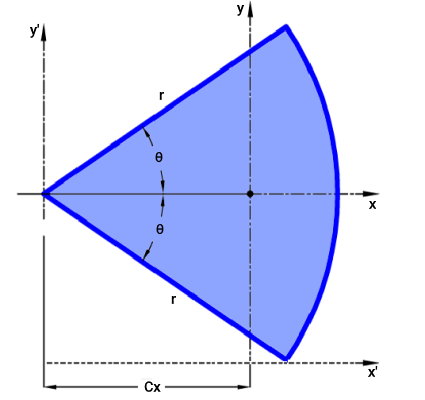
در تصویر بالا، محورهای x و y از مرکز هندسی قطاع عبور میکنند. به علاوه، محور افقی x، نیمساز زاویه مقابل به کمان قطاع است. در واقع، محور x، این زاویه را به دو زاویه برابر θ تبدیل میکند. محورهای 'x و 'y نیز به ترتیب محورهای موازی با x و y هستند.
ممان اینرسی قطاع بالا، از رابطه زیر به دست میآید:
$$
I _ x = \frac { r ^ ۴ } { ۴ } \left( \theta - \frac { ۱ } { ۲ } \sin ( ۲ \theta ) \right )
$$
$$
I _ y = \frac { r ^ ۴ } { ۴ } \left ( \theta + \frac { ۱ } { ۲ } \sin ( ۲ \theta ) \right ) - \frac { ۴ r ^ ۴ } { ۹ \theta } \sin ^ ۲ ( \theta )
$$
- Ix: ممان اینرسی سطح قطاع دایره نسبت به محور مرکزی x
- Iy: ممان اینرسی سطح قطاع دایره نسبت به محور مرکزی y
- r: شعاع قطاع
- θ: نصف زاویه مقابل به کمان قطاع
بر اساس قضیه محورهای موازی، ممان اینرسی مقطع دایره حول محورهای 'x و 'y با استفاده از فرمولهای زیر محاسبه میشود:
$$
I _ { x ^ { ' } } = I _ x + r ^ ۴ \theta \sin ^ ۲ ( \theta )
$$
$$
I _ { y ^ { ' } } = \frac { r ^ ۴ } { ۴ } \left ( \theta + \frac { ۱ }{ ۲ } \sin ( ۲ \theta ) \right )
$$
- $$ I _ { x ^ { ' } } $$: ممان اینرسی سطح قطاع دایره حول محور موازی با محور مرکزی x
- Ix: ممان اینرسی سطح قطاع دایره نسبت به محور مرکزی x
- $$ I _ { y ^ { ' } } $$: ممان اینرسی سطح قطاع دایره حول محور موازی با محور مرکزی y
- r: شعاع قطاع
- θ: نصف زاویه مقابل به کمان قطاع
رابطه ممان اینرسی قطبی قطاع دایره نیز عبارت است از:
$$
J _ { z } = \frac { r ^ ۴ } { ۱۸ } \left ( \frac { ۹ \theta ^ ۲ - ۸ \sin ^ ۲ ( \theta ) } { \theta } \right )
$$
اگر محور مبنای ممان اینرسی سطح قطاع را در محل برخورد دو شعاع و عمود بر سطح در نظر بگیریم، به رابطه زیر میرسیم:
$$
J _ { z ^ { ' } } = \frac { r ^ ۴ \theta }{ ۲ }
$$
- $$ J _ { z } $$: ممان اینرسی سطح قطاع دایره حول محور عمود بر مرکز هندسی
- $$ J _ { z ^ { ' } } $$: ممان اینرسی سطح قطاع دایره حول محور عمود بر تقاطع دو شعاع
- r: شعاع قطاع
- θ: نصف زاویه مقابل به کمان قطاع
در بخشهای بعدی، فرمولهای ممان اینرسی قطاعهای معروف دایره نظیر نیمدایره و ربعدایره را نیز در قالب یک جدول ارائه خواهیم کرد.
مثال ۳: محاسبه ممان اینرسی ربع دایره
ممان اینرسی ربعدایره زیر را به دست بیاورید. محورهای x و y، از مرکز هندسی ربعدایره عبور میکنند. به علاوه، محور x نیمساز زاویه مقابل به کمان ربعدایره است.
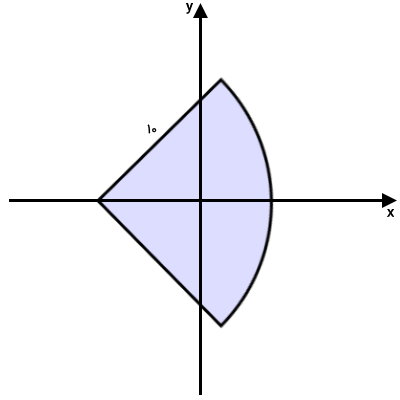
ربعدایره، یکی از قطاعهای دایره است که از تقسیم دایره کامل به چهار قسمت مساوی به دست میآید. بنابراین، زاویه مقابل به کمان این شکل دوبعدی، یکچهارم زاویه دایره (°۹۰=۴÷°۳۶۰) است. فرمول ممان اینرسی قطاع دایره به صورت زیر نوشته میشود:
$$
I _ x = \frac { r ^ ۴ } { ۴ } \left( \theta - \frac { ۱ } { ۲ } \sin ( ۲ \theta ) \right )
$$
$$
I _ y = \frac { r ^ ۴ } { ۴ } \left ( \theta + \frac { ۱ } { ۲ } \sin ( ۲ \theta ) \right ) - \frac { ۴ r ^ ۴ } { ۹ \theta } \sin ^ ۲ ( \theta )
$$
- Ix: ممان اینرسی سطح قطاع دایره نسبت به محور مرکزی x
- Iy: ممان اینرسی سطح قطاع دایره نسبت به محور مرکزی y
- r: شعاع قطاع برابر با ۱۰ واحد
- θ: نصف زاویه مقابل به کمان قطاع برابر با °۴۵=۲÷°۹۰
در روابط بالا، باید مقدار زاویه را بر حسب رادیان بیان کنیم. زاویه ۴۵ درجه، معادل $$ \frac { \pi } { ۴ } $$ در مقیاس رادیان است. به این ترتیب، برای ممان اینرسی حول محور x داریم:
$$
I _ x = \frac { ۱۰ ^ ۴ } { ۴ } \left( \frac { \pi }{ ۴ } - \frac { ۱ } { ۲ } \sin ( ۲ \times \frac { \pi }{ ۴ } ) \right )
$$
$$
I _ x = \frac { ۱۰۰۰۰ } { ۴ } \left( \frac { \pi }{ ۴ } - \frac { ۱ } { ۲ } \sin ( \frac { \pi }{ ۲ } ) \right )
$$
سینوس $$ \frac { \pi } { ۲ } $$ یا همان سینوس زاویه ۹۰ درجه برابر با ۱ است:
$$
I _ x = ۲۵۰۰ \left( \frac { \pi }{ ۴ } - \frac { ۱ } { ۲ } \right )
$$
$$
I _ x = ۲۵۰۰ \left( \frac { ۲ \pi -۲ }{ ۴ } \right )
$$
$$
I _ x = ۶۲۵ \left( ۲ \pi -۲ \right )
$$
$$
I _ x = ۱۲۵۰ \pi - ۱۲۵۰
$$
$$
I _ x \approx ۲۶۷۵
$$
ممان اینرسی ربعدایره حول محور مرکزی x برابر با ۲۶۷۵ واحد طول به توان چهار است. برای ممان اینرسی حول محور y داریم:
$$
I _ y = \frac { ۱۰ ^ ۴ } { ۴ } \left ( \frac { \pi }{ ۴ } + \frac { ۱ } { ۲ } \sin ( ۲ \times \frac { \pi }{ ۴ }) \right ) - \frac { ۴ \times ۱۰ ^ ۴ } { \frac { ۹ \pi }{ ۴ }} \sin ^ ۲ ( \frac { \pi }{ ۴ } )
$$
برای حل عبارت اول در سمت راست رابطه بالا، میتوانیم از عبارتهای نهایی رابطه Ix در مرحله قبل استفاده کنیم:
$$
I _ y = ۶۲۵ \left( ۲ \pi + ۲ \right ) - \frac { ۴ \times ۱۰ ^ ۴ } { \frac { ۹ \pi }{ ۴ }} \sin ^ ۲ ( \frac { \pi }{ ۴ } )
$$
$$
I _ y = ۶۲۵ \left( ۲ \pi + ۲ \right ) - \frac { ۴۰۰۰۰ } { ۷/۰۶۵ } \times \left ( \frac { \sqrt { ۲ } } {۲} \right ) ^ ۲
$$
$$
I _ y = ۶۲۵ \left( ۲ \pi + ۲ \right ) - \frac { ۴۰۰۰۰ } { ۷/۰۶۵ } \times \frac { ۱ } {۲}
$$
$$
I _ y = ۶۲۵ \left( ۲ \pi + ۲ \right ) - \frac { ۲۰۰۰۰ } { ۷/۰۶۵ }
$$
$$
I _ y = ۵۱۷۵ - ۲۸۳۰/۸۶
$$
$$
I _ y \approx ۲۳۴۴
$$
ممان ربعدایره حول محور مرکزی y، تقریبا برابر با ۲۳۴۴ واحد طول به توان چهار شد. دقت داشته باشید که اگر نحوه قرارگیری ربعدایره نسبت به محورهای مرکزی متفاوت و مطابق با شکل زیر بود، فرمولهای ممان اینرسی سطح تغییر میکرد.
ممان اینرسی مقطع ترکیبی دایره
مقطعهای دایرهای، مقاومت بسیار خوبی در برابر بارهای خمشی و پیچشی دارند. از اینرو، اغلب قطعات مکانیکی تحت بارهای خمشی و خمشی، با مقطع دایره ساخته میشوند. در برخی از موارد، حفرههایی را برای کاهش وزن این قطعات در آنها ایجاد میکنند. البته مهرهها و برخی دیگر از قطعات، باید به شکل دایره توخالی ساخته شوند. شکل حفره این مقطعها، میتواند دایرهای، مربعی، ششضلعی یا مقطعهای دیگر (ترجیحا منتظم) باشد. در بخشهای قبلی فرمولهای ممان اینرسی مقطع دایره با حفره دایرهای (حلقه) را معرفی کردیم.
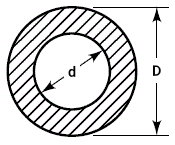
مقطع حلقه، از دو دایره هممرکز تشکیل میشود. حلقه، یک قطر خارجی و یک قطر داخلی دارد. ممان اینرسی سطح دایره بزرگ عبارت است از:
$$
I _ x = \frac { \pi }{ ۶۴ } D ^ ۴
$$
$$
I _ y = \frac { \pi }{ ۶۴ } D ^ ۴
$$
- Ix: گشتاور دوم سطح دایره بزرگ نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح دایره بزرگ نسبت به محور مرکزی y
- D: قطر خارجی دایره بزرگ
اگر دایره کوچک (حفره حلقه)، توپر بود، ممان اینرسی سطح آن از رابطه زیر به دست میآمد:
$$
I _ x = \frac { \pi }{ ۶۴ } d ^ ۴
$$
$$
I _ y = \frac { \pi }{ ۶۴ } d ^ ۴
$$
- Ix: گشتاور دوم سطح دایره بزرگ نسبت به محور مرکزی x
- Iy: گشتاور دوم سطح دایره بزرگ نسبت به محور مرکزی y
- d: قطر خارجی دایره کوچک
ممان اینرسی حلقه، برابر با تفاضل ممان اینرسی دایره بزرگ و ممان اینرسی دایره کوچک است:
$$
I _ x = \frac { \pi }{ ۶۴ } D ^ ۴ - \frac { \pi }{ ۶۴ } d ^ ۴
$$
$$
I _ x = \frac { \pi }{ ۶۴ } ( D ^ ۴ - d ^ ۴ )
$$
$$
I _ y = \frac { \pi }{ ۶۴ } D ^ ۴ - \frac { \pi }{ ۶۴ } d ^ ۴
$$
$$
I _ y = \frac { \pi }{ ۶۴ } ( D ^ ۴ - d ^ ۴ )
$$
اگر حفره درون دایره، به هر شکل دیگری بود نیز فرمول ممان اینرسی مقطع توخالی، به همین روش (تفاضل ممانهای اینرسی) به دست میآمد. به عنوان مثال، یک ششضلعی منتظم به ضلع a را در نظر بگیرید.
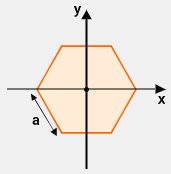
فرمول ممان اینرسی شش ضلعی منتظم حول محورهای مرکزی x و y عبارت است از:
$$
I = \frac { ۵ \sqrt { ۳ } } { ۱۶ } a ^ ۴
$$
- I: گشتاور دوم سطح ششضلعی منتظم نسبت به محورهای مرکزی x و y
- a: اندازه ضلع ششضلعی منتظم
اکنون، یک مقطع دایرهای با حفرهای به شکل ششضلعی منتظم را در نظر بگیرید.
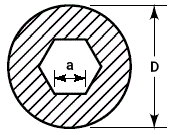
ممان اینرسی سطح بالا از تفاضل ممان اینرسی دایره و ممان اینرسی ششضلعی منتظم به دست میآید:
$$
I = \frac { \pi }{ ۶۴ } D ^ ۴ - \frac { ۵ \sqrt { ۳ } } { ۱۶ } a ^ ۴
$$
توجه داشته باشید که به دست آوردن ممان اینرسی با این روش، فقط برای حفرههای دارای تقارن محوری و یا مرکزی امکانپذیر است. به علاوه، مقطع بزرگ و حفره، باید هممرکز باشند.
مثال ۴: محاسبه ممان اینرسی مقطع دایره ای با حفره مربعی
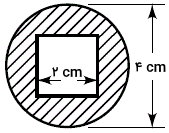
ممان اینرسی مقطع زیر را به دست بیاورید. حفره درون مقطع، یک مربع بوده و سطح دایرهای هممرکز است. عدد پی را برابر با ۳/۱۴ در نظر بگیرید.
فرمول ممان اینرسی دایره عبارت است از:
$$
I _ c = \frac { \pi }{ ۶۴ } D ^ ۴
$$
- Ic: گشتاور دوم سطح دایره نسبت به محور مرکزی
- D: قطر دایره برابر با ۴ سانتیمتر
فرمول ممان اینرسی مربع نیز به صورت زیر نوشته میشود:
$$
I _ s = \frac { a ^ ۴ }{ ۱۲ }
$$
- Is: گشتاور دوم سطح مربع نسبت به محور مرکزی
- a: ضلع مربع برابر با ۲ سانتیمتر
به این ترتیب، ممان اینرسی مقطع توخالی بالا، از تفاضل ممان اینرسی دایره و مربع داخل آن به دست میآید:
$$
I = I _ c - I _ s
$$
$$
I = \frac { \pi }{ ۶۴ } D ^ ۴ - \frac { a ^ ۴ }{ ۱۲ }
$$
$$
I = \frac { \pi ۴ ^ ۴ }{ ۶۴ } - \frac { ۲ ^ ۴ }{ ۱۲ }
$$
$$
I = \frac { ۳/۱۴ \times ۲۵۶ }{ ۶۴ } - \frac { ۱۶ }{ ۱۲ }
$$
$$
I = ( ۳/۱۴ \times ۴ ) - \frac { ۴ }{ ۳ }
$$
$$
I = ۱۲/۵۶ - ۱/۳۳
$$
$$
I \approx ۱۱/۲۳
$$
در نتیجه، ممان اینرسی مقطع دایرهای با حفره مربعی هممرکز برابر با ۱۱/۲۳ سانتیمتر به توان چهار (۱۱/۲۳cm۴) است.
محاسبه آنلاین ممان اینرسی سطح و ممان اینرسی قطبی دایره
یکی از روشهای مفید برای یادگیری مبحث ممان اینرسی مقطع دایره و تمرین مثالهای مختلف، استفاده از ابزارهای اینترنتی است. از سایتهای کاربردی در این زمینه میتوان به OmniCalculator اشاره کرد. در این سایت، چندین ماشینحساب کاربردی و تخصصی برای محاسبه ممان اینرسی سطح شکلهای مختلف و کمیتهای وابسته به آن وجود دارند. تصویر زیر ماشین حساب ممان اینرسی مقاطع (+) را نمایش میدهد.
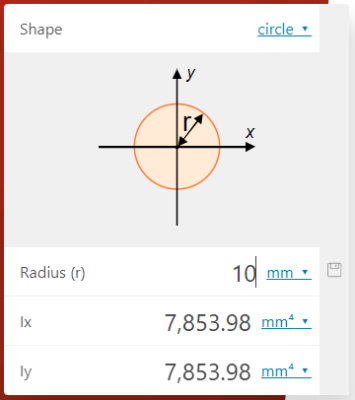
فهرست بازشونده مقابل عنوان «Shape»، امکان انتخاب شکل مورد نظر را فراهم میکند. در تصویر بالا، این گزینه بر روی شکل دایره (circle) قرار دارد. پس از انتخاب شکل، پارامترهای مورد نیاز برای محاسبه گشتاور دوم سطح ظاهر میشوند. به منظور محاسبه گشتاور دوم سطح دایره، فقط باید اندازه شعاع را وارد کنید. به عنوان مثال، با تایپ عدد ۱۰ در کادر مقابل عنوان «Radius»، مقدار ممانهای اینرسی دایرهای به شعاع ۱۰ (با واحد انتخابی دلخواه) در دو کادر دیگر به نمایش درمیآید. تصویر زیر، نمایی از ماشینحساب ممان اینرسی قطبی OmniCalculator (+) برای مقطع جدار نازک دایرهای است. با واردن کردن شعاع داخلی و خارجی یا قطر داخلی و خارجی، مقدار ممان اینرسی قطبی محاسبه میشود.
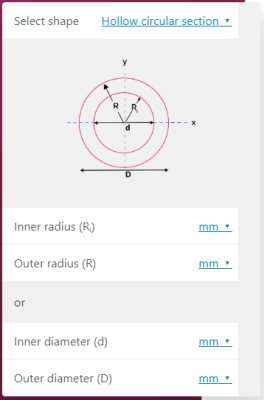
OmniCalculator، یکی از چندین سایت ارائهکننده ماشینحسابهای اینترنتی است که میتواند شما را در انجام محاسبات مهندسی کمک کند. اگر قصد انجام محاسبات ساده تا پیچیده مهندسی توسط کامپیوتر را دارید، نرمافزارهای تخصصی نظیر متلب نیز از گزینههای خوب به شمار میروند.
جدول ممان اینرسی قطاع های دایره
در بخشهای، با فرمولهای مختلف ممان اینرسی دایره توپر و قطاعهای آن آشنا شدید. در این بخش، این فرمولها را در قالب یک جدول معرفی میکنیم.
| مقطع | شکل | فرمول ممان اینرسی سطح | فرمول ممان اینرسی قطبی | توضیحات |
| دایره توپر |
 |
$$ $$ | $$ I _ z = \frac { \pi } { ۲ } r ^ ۴ $$ | - |
| حلقه دایرهای |
 |
$$ $$ | $$ I _ z = \frac { \pi } { ۲ } \left ( r _ ۲ ^ ۴ - r _ ۱ ^ ۴ \right ) $$ | - |
| تیوب (دایره جدار نازک) |
 | $$ I _ x = I _ y \approx \pi r ^ ۳ t $$ | - | در دایره جدار نازک، شعاع داخلی و خارجی بسیار نزدیک هستند و میتوان آنها را تقریبا برابر در نظر گرفت. |
| قطاع با محورهای گذرنده از تقاطع قاعدهها |
 | $$ I _ x = ( \theta - \sin \theta ) \frac { r ^ ۴ }{ ۸ } $$ | - | این فرمول فقط برای $$ ۰ \le \theta \le ۲ \pi $$ قابل استفاده است. |
| نیم دایره توپر با محورهای مرکزی x و y |
 |
$$ $$ | - | محورهای x و y از مرکز هندسی نیمدایره عبور میکنند. |
| نیم دایره با محور افقی منطبق بر قطر |
 |
$$ $$ | - | محور y از مرکز هندسی نیمدایره عبور میکند و محور x بر روی قطر نیمدایره منطبق است. |
| ربع دایره با محورهای مرکزی x و y |
 |
$$ $$ | - | محورهای x و y از مرکز هندسی ربعدایره عبور میکنند. |
| ربع دایره با محورهای منطبق بر شعاع |
 |
$$ $$ | - | - |
در صورت تمایل به یادگیری راجع به ممان اینرسی مقاطع مستطیلی، مطالعه مطلب «ممان اینرسی مستطیل – فرمول و محاسبه + مثال و حل تمرین» را به شما پیشنهاد میکنیم.
سوالات متداول در رابطه با ممان اینرسی دایره
در این بخش، به برخی از پرتکرارترین سوالات مرتبط با ممان اینرسی دایره به طور خلاصه پاسخ میدهیم.
تعریف ممان اینرسی مقطع دایره چیست ؟
ممان اینرسی مقطع دایره، کمیتی برای نمایش میزان پراکندگی نقاط سطح دایره نسبت به یک محور مشخص است.
فرمول ممان اینرسی سطح دایره چیست ؟
فرمول ممان اینرسی سطح دایره، I=πr^۴/۴ است.
فرمول ممان اینرسی سطح حلقه شکل چیست ؟
فرمول ممان اینرسی حلقه، برابر با تفاضل ممان اینرسی سطح دایره توپر و سطح حفره است.
فرمول ممان اینرسی نیم دایره چیست ؟
فرمول ممان اینرسی نیمدایره حول محور مرکزی x برابر با ۰/۱۰۹۸r^۴ و حول محور مرکزی y برابر با πr^۴/۸ است.
فرمول ممان اینرسی ربع دایره چیست ؟
فرمول ممان اینرسی ربعدایره حول محور مرکزی x و y برابر با ۰/۰۵۴۹r^۴ است.
رابطه بین ممان اینرسی دایره و نیم دایره چیست ؟
اگر بدون تغییر محورهای مبنا، یک دایره را بر روی محور مرکزی x نصف کنیم، ممان اینرسی آن حول محورهای x و y نصف میشود.
قضیه محورهای موازی در محاسبه ممان اینرسی مقطع دایره ای چیست ؟
قضیه محورهای موازی، رابطه بین ممان اینرسی دایره حول محورهای مرکزی و محورهای موازی با آنها است. با کمک این رابطه، در صورت داشتن فاصله بین محور مبنای دلخواه با محور مرکزی، میتوان ممان اینرسی جدید را به دست آورد.










