مشتق e – به زبان ساده + مثال و حل تمرین
مشتق e به توان x، برابر با خودش است. عبارت ex، یک تابع نمایی را نمایش میدهد. اگر بخواهیم مشتق این تابع را بر حسب x به دست بیاوریم، به عبارت ex میرسیم. این نتیجه، یکی از ویژگیهای مخصوص توابع نمایی است. در این مقاله، مفاهیم مرتبط با مشتق e به توان x و نحوه مشتقگیری از شکلهای دیگر این تابع نمایی را به همراه چندین مثال و تمرین آموزش میدهیم.
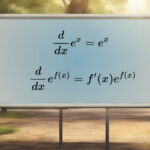
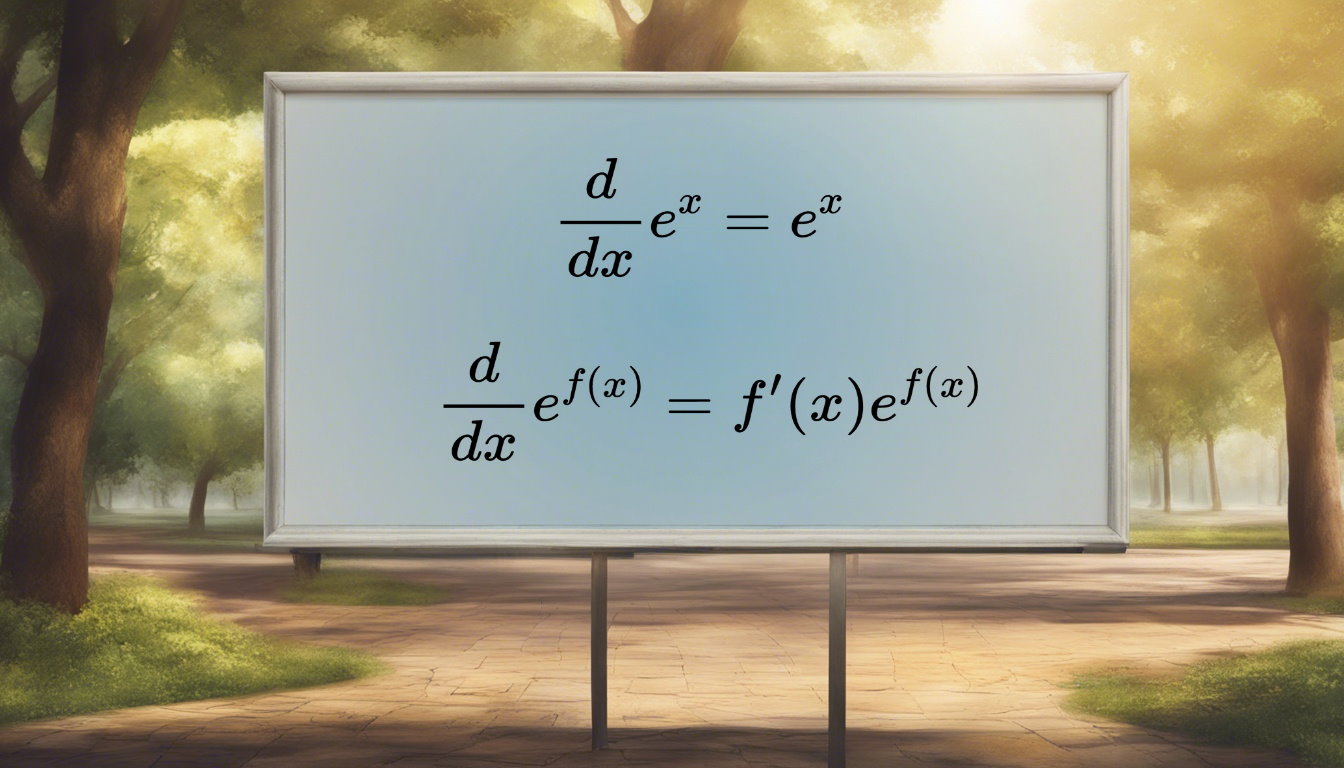
e چیست ؟
e، یکی از ثابتهای عددی معروف در دنیای ریاضی و برابر با ۲/۷۱۸۲۸ است. با محاسبه حد عبارت زمانی که n به بینهایت میل میکند، مقدار این ثابت به دست میآید. امکان محاسبه e از روی جمع عبارتهای سری بینهایت زیر نیز وجود دارد:
ثابت e، با عنوان عدد اویلر یا عدد نپر نیز شناخته میشود. این عدد، مبنای لگاریتمهای طبیعی است.
تابع نمایی و تابع نمایی e چیست ؟
تابع نمایی، یکی از مهمترین توابع ریاضی به شمار میرود. در توابع نمایی، متغیر به صورت توان در عبارتها ظاهر میشود. این توان میتواند هر عدد حقیقی باشد. فرم کلی توابع نمایی به صورت زیر است:
تصویر زیر، نمودار تابع نمایی را نمایش میدهد.
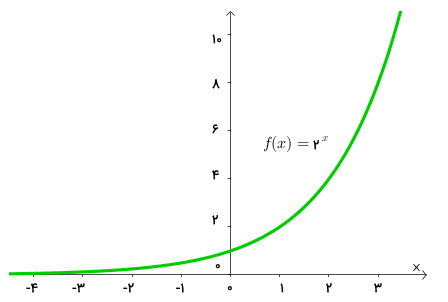
اگر عدد ثابت در فرم کلی تابع نمایی را برابر با عدد اویلر قرار دهیم، تابع نمایی به شکل زیر درمیآید:
این تابع به صورت زیر نیز نوشته میشود:
فرم کلی تابع e به شکل زیر است:
a، ضریب عددی و c، ثابت عددی را نمایش میدهد. مشتق e، یک ویژگی جالب دارد که در بخش بعدی به آن میپردازیم.
مشتق e چیست ؟
مشتق تابع نمایی ، یکی از ویژگیهای منحصر به فرد این تابع است. مشتق برابر با خودش میشود. به عبارت دیگر:
این ویژگی را میتوان به شکلهای دیگر نیز بیان کرد:
- شیب نمودار در هر نقطه، برابر با ارتفاع تابع در همان نقطه است.
- نرخ افزایش تابع در نقطه x، برابر با مقدار تابع در نقطه x است.
مشتق e با ضریب ثابت
تابع نمایی زیر را در نظر بگیرید:
c ضریب عدد ثابت را نمایش میدهد. مشتق تابع بالا عبارت است از:
به عبارت دیگر، مشتق e به توان x با ضریب ثابت نیز با خودش برابر میشود.
مثال ۱: تعیین مشتق e با ضریب ثابت
مشتق تابع را به دست بیاورید.
تابع ، از یک ضریب ثابت (عدد ۳) و عبارت نمایی تشکیل میشود. مشتق این تابع، از رابطه زیر به دست میآید:
یا
در نتیجه، مشتق ، برابر با خودش، یعنی است.
تمرین و آزمون

فرمول کلی مشتق e به توان f(x)
اگر توان تابع e، تابعی مانند u(x)، مشتق e بر حسب x از رابطه زیر به دست میآید:
یا
نحوه به کارگیری فرمول بالا را با حل یک مثال و تمرین آموزش میدهیم.
مثال ۲: تعیین مشتق e به توان ۲x
مشتق تابع را تعیین کنید.
برای به دست آوردن مشتق تابع باید از فرمول کلی مشتق e استفاده کنیم. این فرمول به صورت زیر نوشته میشود:
در رابطه بالا، u(x) برابر میشود با:
این عبارت را درون رابطه جایگذاری میکنیم:
تابع ، یک تابع خطی است. مشتق این تابع برابر است با:
نتیجه را در رابطه مشتق قرار میدهیم:
در نتیجه، مشتق برابر با است.
تصویر زیر، منحنی چند تابع نمایی با پایه e و توانهای متفاوت را نمایش میدهد.
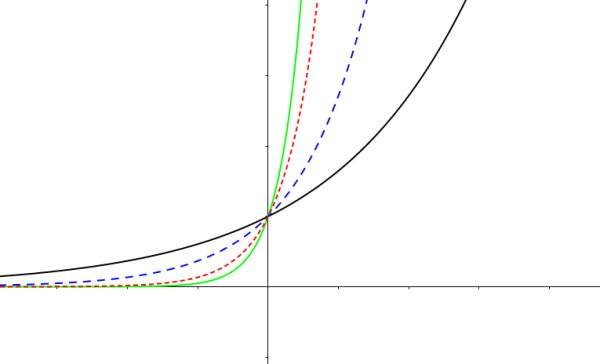
تمرین و آزمون
حل تمرین و مثال مشتق e
به منظور آشنایی بهتر با فرمولهای مشتق e، به حل چند مثال و تمرین بیشتر میپردازیم.
مثال ۳: تعیین مشتق e به توان منفی x
مشتق تابع را به دست بیاورید.
فرم تابع مورد سوال به صورت زیر است:
مشتق این تابع، توسط رابطه زیر تعیین میشود:
با توجه به این اطلاعات داریم:
به این ترتیب:
g(x) و g'(x) را درون رابطه f'(x) قرار میدهیم:
تمرین و آزمون
مثال ۴: مشتق e به توان sinx
مشتق را به دست بیاورید.
توان e در تابع مورد سوال (عبارت )، تابعی از x است. به عبارت دیگر:
به این ترتیب، میتوانیم تابع مورد سوال را به صورت زیر بنویسیم:
بر اساس قواعد مشتق توابع مثلثاتی، مشتق این تابع از رابطه زیر به دست میآید:
f'(x) عبارت است از:
f(x) و f'(x) را درون رابطه مشتق تابع قرار میدهیم:
تمرین و آزمون

مشتق معکوس e چگونه بدست می آید ؟
معکوس تابع نمایی ex، یک تابع لگاریتمی بر مبنای e است. این تابع با عنوان لگاریتم طبیعی شناخته شده و با ln نمایش داده میشود:
مشتق معکوس ex یا همان مشتق لگاریتم طبیعی ، عبارت است از:
در صورت وجود ضریب ثابت عددی (مانند ضریب c) در کنار x، فرمول مشتق معکوس e، تغییری نخواهد کرد:
اگر به جای x در ln، تابعی مانند f(x) قرار داشته باشد، فرمول مشتق به شکل زیر درمیآید:
مثال ۵: تعیین مشتق ln
مشتق را به دست بیاورید.
تابع مورد سوال، یک لگاریتم طبیعی است. در این لگاریتم، یک چندجملهای قرار دارد. اگر چندجملهای را برابر با g(x) قرار دهیم:
مشتق تابع از رابطه زیر به دست خواهد آمد:
برای استفاده از تابع بالا، ابتدا باید مشتق g(x) را تعیین کنیم:
اکنون، عبارتهای g(x) و g'(x) را درون رابطه مشتق ln قرار میدهیم:
به این ترتیب، مشتق تابع لگاریتم طبیعی را به دست آوردیم.

اثبات فرمول مشتق e با حد و پیوستگی
در این بخش، قصد داریم مشتق تابع ex (رابطه زیر) را اثبات کنیم:
برای شروع، تعریف حدی مشتق را در نظر میگیریم:
تابع اصلی در اینجا عبارت است از:
بنابراین:
با جایگذاری این عبارتها درون رابطه حدی مشتق، به رابطه زیر میرسیم:
با توجه به خواص توان در ریاضی، میتوانیم عبارت را به صورت زیر بازنویسی کنیم:
به این ترتیب، داریم:
از عبارت ex در صورت کسر، فاکتور میگیریم:
از آنجایی که ex در Δx ظاهر نمیشود، میتوانیم آن را به پشت حد انتقال دهیم:
جواب نهایی مشتق بالا، با تعیین حد زیر به دست میآید:
برای تعیین حد بالا، ابتدا تغییر متغیر زیر را انجام میدهیم:
در عبارت بالا، اگر Δx به صفر میل کند، عبارت eΔx برابر با ۱ و متغیر n برابر با ۰ میشود. به عبارت دیگر:
جواب حد بالا را به خاطر داشته باشید. اکنون، تغییر متغیر را بر حسب eΔx بازنویسی میکنیم:
از هر دو طرف معادله بالا، ln میگیریم:
سمت چپ معادله بالا را بر اساس فرمول مشتق ln ساده میکنیم:
عبارت بالا را به همراه تغییر متغیر در رابطه حدی مشتق قرار میدهیم:
عبارت سمت راست را بازنویسی میکنیم:
بر اساس قانون توان در لگاریتم، میتوانیم ضریب پشت ln را به عنوان توان عبارت داخل آن در نظر بگیریم:
با توجه به قانون تقسیم در حد، عبارتهای بالا را به صورت زیر مینویسیم:
صورت کسر بالا برابر با ۱ است. بر اساس قانون حد ترکیب توابع میتوانیم مخرج کسر را به صورت ترکیب حد بازنویسی کنیم:
جواب حد در مخرج کسر بالا، یکی از تعریفهای ثابت اویلر (e) است:
از اینرو، به جای این حد، عبارت e را قرار میدهیم:
در نتیجه:
جواب حد را در آخرین رابطه حدی مشتق قرار میدهیم:
همانطور که مشاهده میکنید، مشتق ex برابر با خودش (ex) شد.

سوالات متداول در رابطه با مشتق e
در این بخش، به برخی از پرتکرارترین سوالات در رابطه با مبحث مشتق e به طور مختصر پاسخ میدهیم.
e چیست ؟
e، ثابت عددی اویلر و برابر با ۲/۷۱۸۲۸ است.
مشتق e به توان x چیست ؟
مشتق e به توان x یا e^x، برابر با خودش (e^x) است.
مشتق کدام تابع برابر با خودش است ؟
مشتق دو تابع f(x)=۰ و f(x)=ex برابر با خودش است.
فرمول مشتق e به توان f(x) چیست ؟
فرمول مشتق e به توان f(x) برابر با f'(x)e^(f(x) است.
معکوس e به توان x چیست ؟
تابع معکوس e به توان x، لگاریتم طبیعی ln x است.
مشتق معکوس e به توان x چیست ؟
مشتق معکوس e به توان x (مشتق ln x)، برابر با یک بر روی x یا یک x ام است.
آزمون مشتق e
۱. عدد e چه نوع عددی در ریاضیات است؟
یک عدد صحیح مثبت است که فقط برای محاسبات انتگرال استفاده میشود.
یک عدد ثابت ریاضی است که مبنای لگاریتمهای طبیعی میباشد.
یک عدد مختلط مهم است که برای نمایش بردارها کاربرد دارد.
یک عدد گنگ هندسی است که تنها در فرمولهای مثلثاتی دیده میشود.
عدد e عدد ثابتی است که مقدار تقریبی ۲٫۷۱۸۲۸ دارد و پایه لگاریتمهای طبیعی است.
۲. کدام خصوصیت تابع نمایی باعث یگانگی مشتق آن در میان توابع ریاضی میشود؟
مشتق تابع همیشه مقدار ثابتی دارد.
تابع فقط مقادیر مثبت میگیرد.
مشتق تابع همیشه برابر خودش است.
پایه تابع عدد نپر است.
آنچه تابع نمایی را منحصر به فرد میکند این است که مشتق آن دقیقا برابر با خودش یعنی همان است و هیچ تابع دیگری این ویژگی را ندارد.
۳. در رابطه تابع نمایی هر بخش چه نقشی بر رفتار تابع دارد؟
ضریب a فقط مقدار تابع را در x=0 تغییر میدهد و c هیچ تاثیری ندارد.
عدد c شیب تابع را تغییر میدهد و a فقط شکل نمودار را تغییر میدهد.
عدد c مبنای نمایی را تغییر میدهد و a مقدار تابع را کم یا زیاد میکند.
ضریب a میزان کشیدگی یا فشردگی نمودار و c جابهجایی عمودی را تعیین میکند.
در ضریب a باعث کشیده شدن یا فشرده شدن نمودار تابع نمایی بر محور y میشود و c موجب جابهجایی عمودی کل نمودار میگردد.
۴. برای مشتقگیری از تابعی به فرم چرا باید از قاعده زنجیرهای استفاده کنیم؟
چون فرمول مشتق توابع نمایی برای همه حالات یکسان است و تابع داخلی تاثیری ندارد.
چون مشتق صرفا برابر است و نیازی به مشتق تابع داخلی ندارد.
چون مقدار تابع داخلی f(x) همیشه ثابت در نظر گرفته میشود.
چون مشتق حاصلضرب مشتق f(x) و است و f(x) خودش تابعی از x میباشد.
زمانی که تابع به صورت باشد، چون f(x) خودش تابعی از x است، مشتقگیری نیازمند استفاده از قاعده زنجیرهای میشود. زیرا مشتق این عبارت برابر با حاصلضرب مشتق تابع داخلی «مشتق f(x)» در خود تابع نمایی است.
۵. رابطه مشتق تابع نمایی با شیب نمودار آن در هر نقطه چیست؟
مشتق همیشه کمتر از مقدار تابع در همان نقطه است.
مقدار مشتق فقط در نقطه x=0 با مقدار تابع برابر است.
شیب نمودار در هر نقطه برابر مقدار تابع در همان نقطه است.
مشتق تابعی کاملا متفاوت از خود را نشان میدهد.
در تابع هر نقطهای از نمودار دارای شیبی است که دقیقا با مقدار همان تابع برابر است.
۶. اگر بخواهیم مشتق تابع را به دست آوریم، مراحل صحیح محاسبه کدام است؟
ابتدا ۵ را حذف کرده و مشتق را حساب میکنیم.
ابتدا مشتق ۲x را به دست آورده، سپس آن را در ضرب میکنیم.
مقدار مشتق برابر با است و باید در ۵ ضرب شود.
مشتق برابر ۵ است چون مشتق صفر میشود.
برای مشتقگیری از تابع ابتدا باید بدانیم مشتق تابع به فرم برابر با است. در اینجا مشتق ۲x نسبت به x برابر ۲ است. پس حاصل ضرب این عدد در ما را به نتیجه میرساند.













خیلی عالی بود ومک عدد نیپر ومشتق آن فهمیدم
نوشتار صفحه بهم ریخته
با سلام؛
از بازخورد شما بسیار سپاسگزاریم. این مورد با بخش فنی هماهنگ و رفع شد.
با تشکر از همراهی شما با مجله فرادرس
مشتق مجهول x ضربدر e منفی x
عالی بود یک ساعت دیگه امتحانمه و منو از گیجی نجات داد