قبلاً در مجموعه آموزشهای ریاضیات مجله فرادرس با توابع هذلولوی یا هیپربولیک آشنا شدیم و مشتق این توابع را بهطور بسیار خلاصه بررسی کردیم. در این آموزش، مشتق توابع هذلولوی و معکوس آنها را با تفصیل بیشتری بیان خواهیم کرد.
از آنجایی که توابع هذلولوی براساس توابع نمایی e x e^x e x e − x e^{-x} e − x
sinh x = e x – e – x 2 , cosh x = e x + e – x 2 . {\sinh x = \frac{{{e^x} – {e^{ – x}}}}{2},\;\;\;}\kern-0.3pt{\cosh x = \frac{{{e^x} + {e^{ – x}}}}{2}.} sinh x = 2 e x – e – x , cosh x = 2 e x + e – x .
مشتق این توابع نیز بهصورت زیر است:
( sinh x ) ′ = ( e x – e – x 2 ) ′ = e x + e – x 2 = cosh x , ( cosh x ) ′ = ( e x + e – x 2 ) ′ = e x – e – x 2 = sinh x . {{\left( {\sinh x} \right)^\prime } = {\left( {\frac{{{e^x} – {e^{ – x}}}}{2}} \right)^\prime } } = {\frac{{{e^x} + {e^{ – x}}}}{2} = \cosh x,\;\;\;}\kern-0.3pt {{\left( {\cosh x} \right)^\prime } = {\left( {\frac{{{e^x} + {e^{ – x}}}}{2}} \right)^\prime } } = {\frac{{{e^x} – {e^{ – x}}}}{2} = \sinh x.} ( sinh x ) ′ = ( 2 e x – e – x ) ′ = 2 e x + e – x = cosh x , ( cosh x ) ′ = ( 2 e x + e – x ) ′ = 2 e x – e – x = sinh x .
مشتق تانژانت هیپربولیک را نیز میتوان با استفاده از تعریف بهصورت زیر محاسبه کرد:
( tanh x ) ′ = ( sinh x cosh x ) ′ = ( sinh x ) ′ cosh x – sinh x ( cosh x ) ′ cosh 2 x = cosh x ⋅ cosh x – sinh x ⋅ sinh x cosh 2 x = cosh 2 x – sinh 2 x cosh 2 x . {{\left( {\tanh x} \right)^\prime } = {\left( {\frac{{\sinh x}}{{\cosh x}}} \right)^\prime } } = {\frac{{{{\left( {\sinh x} \right)}^\prime }\cosh x – \sinh x{{\left( {\cosh x} \right)}^\prime }}}{{{{\cosh }^2}x}} } = {\frac{{\cosh x \cdot \cosh x – \sinh x \cdot \sinh x}}{{{{\cosh }^2}x}} } = {\frac{{{{\cosh }^2}x – {{\sinh }^2}x}}{{{{\cosh }^2}x}}.} ( tanh x ) ′ = ( cosh x sinh x ) ′ = cosh 2 x ( sinh x ) ′ cosh x – sinh x ( cosh x ) ′ = cosh 2 x cosh x ⋅ cosh x – sinh x ⋅ sinh x = cosh 2 x cosh 2 x – sinh 2 x .
همانطور که میدانیم، رابطه دو تابع سینوس هیپربولیک و کسینوس هیپربولیک بهصورت زیر است:
cosh 2 x – sinh 2 x = 1 {\cosh ^2}x – {\sinh ^2}x = 1 cosh 2 x – sinh 2 x = 1
بنابراین، مشتق تانژانت هیپربولیک را میتوانیم بهصورت زیر بنویسیم:
( tanh x ) ′ = cosh 2 x – sinh 2 x cosh 2 x = 1 cosh 2 x = sech 2 x . {{\left( {\tanh x} \right)^\prime } }={ \frac{{{{\cosh }^2}x – {{\sinh }^2}x}}{{{{\cosh }^2}x}} } = {\frac{1}{{{{\cosh }^2}x}} } = {{\text{sech}^2}x.} ( tanh x ) ′ = cosh 2 x cosh 2 x – sinh 2 x = cosh 2 x 1 = sech 2 x .
به طریق مشابه، سایر توابع هذلولوی اصلی را میتوان به صورت زیر محاسبه کرد:
( coth x ) ′ = ( cosh x sinh x ) ′ = ( cosh x ) ′ sinh x – cosh x ( sinh x ) ′ sinh 2 x = – cosh 2 x – sinh 2 x sinh 2 x = – 1 sinh 2 x = – csch 2 x , {{\left( {\coth x} \right)^\prime } }={ {\left( {\frac{{\cosh x}}{{\sinh x}}} \right)^\prime } } = {\frac{{{{\left( {\cosh x} \right)}^\prime }\sinh x – \cosh x{{\left( {\sinh x} \right)}^\prime }}}{{{{\sinh }^2}x}} } = { – \frac{{{{\cosh }^2}x – {{\sinh }^2}x}}{{{{\sinh }^2}x}} } = { – \frac{1}{{{{\sinh }^2}x}} } = { – {\text{csch}^2}x,} ( coth x ) ′ = ( sinh x cosh x ) ′ = sinh 2 x ( cosh x ) ′ sinh x – cosh x ( sinh x ) ′ = – sinh 2 x cosh 2 x – sinh 2 x = – sinh 2 x 1 = – csch 2 x ,
( sech x ) ′ = ( 1 cosh x ) ′ = – 1 cosh 2 x ⋅ ( cosh x ) ′ = – 1 cosh 2 x ⋅ sinh x = – 1 cosh x ⋅ sinh x cosh x = –sech x tanh x , {{\left( {\text{sech}\,x} \right)^\prime } }={ {\left( {\frac{1}{{\cosh x}}} \right)^\prime } } = { – \frac{1}{{{{\cosh }^2}x}} \cdot {\left( {\cosh x} \right)^\prime } } = { – \frac{1}{{{{\cosh }^2}x}} \cdot \sinh x } = { – \frac{1}{{\cosh x}} \cdot \frac{{\sinh x}}{{\cosh x}} } = { – \text{sech}\,x\tanh x,} ( sech x ) ′ = ( cosh x 1 ) ′ = – cosh 2 x 1 ⋅ ( cosh x ) ′ = – cosh 2 x 1 ⋅ sinh x = – cosh x 1 ⋅ cosh x sinh x = – sech x tanh x ,
( csch x ) ′ = ( 1 sinh x ) ′ = – 1 sinh 2 x ⋅ ( sinh x ) ′ = – 1 sinh 2 x ⋅ cosh x = – 1 sinh x ⋅ cosh x sinh x = –csch x coth x ( x ≠ 0 ) . {{\left( {\text{csch}\,x} \right)^\prime } }={ {\left( {\frac{1}{{\sinh x}}} \right)^\prime } } = { – \frac{1}{{{\sinh^2}x}} \cdot {\left( {\sinh x} \right)^\prime } } = { – \frac{1}{{{\sinh^2}x}} \cdot \cosh x } = { – \frac{1}{{\sinh x}} \cdot \frac{{\cosh x}}{{\sinh x}} } = { – \text{csch}\,x\coth x\;\;}\kern-0.3pt{\left( {x \ne 0} \right).} ( csch x ) ′ = ( sinh x 1 ) ′ = – sinh 2 x 1 ⋅ ( sinh x ) ′ = – sinh 2 x 1 ⋅ cosh x = – sinh x 1 ⋅ sinh x cosh x = – csch x coth x ( x = 0 ) .
همانطور که میبینیم، مشتق توابع هذلولوی، بسیار شبیه مشتق توابع مثلثاتی است. البته باید به تفاوت علامتها دقت کنید؛ مشتق تابع کسینوس به صورت زیر است:
( cos x ) ′ = – sin x {\left( {\cos x} \right)^\prime } = – \sin x ( cos x ) ′ = – sin x
اما برای کسینوس هیپربولیک، علامت منفی وجود ندارد:
( cosh x ) ′ = sinh x . {\left( {\cosh x} \right)^\prime } = \sinh x. ( cosh x ) ′ = sinh x .
برای تابع سکانت و سکانت هیپربولیک شرایط دقیقاً برعکس است:
( sec x ) ′ = sec x tan x , ( sech x ) ′ = –sech x tanh x . {{{\left( {\sec x} \right)^\prime } = \sec x\tan x,\;\;\;}}\kern-0.3pt {{{\left( {\text{sech}\,x} \right)^\prime } }={ – \text{sech}\,x\tanh x.}} ( sec x ) ′ = sec x tan x , ( sech x ) ′ = – sech x tanh x .
مشتق معکوس توابع هذلولوی
اکنون، مشتق معکوس ۶ تابع هذلولوی را بررسی میکنیم. این مشتقها را میتوان با استفاده از قضیه تابع معکوس بهدست آورد.
برای مثال، تابع معکوس سینوس هیپربولیک y = f ( x ) = a r c s i n h x y = f\left( x \right)=\mathrm{arcsinh} \, x y = f ( x ) = arcsinh x x = φ ( y ) = a r c s i n h y x = \varphi \left( y \right)=\mathrm{arcsinh} \, y x = φ ( y ) = arcsinh y
( arcsinh x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( sinh y ) ′ = 1 cosh y = 1 1 + sinh 2 y = 1 1 + sinh 2 ( arcsinh x ) = 1 1 + x 2 . {{\left( {\text{arcsinh}\,x} \right)^\prime } }={ f’\left( x \right) } = {\frac{1}{{\varphi’\left( y \right)}} } = {\frac{1}{{{{\left( {\sinh y} \right)}^\prime }}} } = {\frac{1}{{\cosh y}} } = {\frac{1}{{\sqrt {1 + {\sinh^2}y} }} }\\ = {\frac{1}{{\sqrt {1 + {\sinh^2}\left( {\text{arcsinh}\,x} \right)} }} } = {\frac{1}{{\sqrt {1 + {x^2}} }}.} ( arcsinh x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( sinh y ) ′ 1 = cosh y 1 = 1 + sinh 2 y 1 = 1 + sinh 2 ( arcsinh x ) 1 = 1 + x 2 1 .
به طریق مشابه، میتوانیم مشتق معکوس سه تابع کسینوس هیپربولیک، تانژانت هیپربولیک و کتانژانت هیپربولیک را بهصورت زیر محاسبه کنیم:
( arccosh x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( cosh y ) ′ = 1 sinh y = 1 cosh 2 y – 1 = 1 cosh 2 ( arccosh x ) – 1 = 1 x 2 – 1 ( x > 1 ) , {{\left( {\text{arccosh}\,x} \right)^\prime } }={ f’\left( x \right) } = {\frac{1}{{\varphi’\left( y \right)}} } = {\frac{1}{{{{\left( {\cosh y} \right)}^\prime }}} } = {\frac{1}{{\sinh y}} } = {\frac{1}{{\sqrt {{\cosh^2}y – 1} }} } = {\frac{1}{{\sqrt {{\cosh^2}\left( {\text{arccosh}\,x} \right) – 1} }} } = {\frac{1}{{\sqrt {{x^2} – 1} }}\;\;\left( {x \gt 1} \right),} ( arccosh x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( cosh y ) ′ 1 = sinh y 1 = cosh 2 y –1 1 = cosh 2 ( arccosh x ) –1 1 = x 2 –1 1 ( x > 1 ) ,
( arctanh x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( tanh y ) ′ = 1 1 cosh 2 y = cosh 2 y . {{\left( {\text{arctanh}\,x} \right)^\prime } }={ f’\left( x \right) } = {\frac{1}{{\varphi’\left( y \right)}} } = {\frac{1}{{{{\left( {\tanh y} \right)}^\prime }}} } = {\frac{1}{{\frac{1}{{{{\cosh }^2}y}}}} } = {{\cosh ^2}y.} ( arctanh x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( tanh y ) ′ 1 = c o s h 2 y 1 1 = cosh 2 y .
اگر از اتحاد cosh 2 y – sinh 2 y = 1 {\cosh ^2}y – {\sinh ^2}y = 1 cosh 2 y – sinh 2 y = 1
1 – tanh 2 y = 1 cosh 2 y or cosh 2 y = 1 1 – tanh 2 y . {1 – {\tanh ^2}y = \frac{1}{{{{\cosh }^2}y}}\;\;}\kern-0.3pt {\text{or}\;\;{\cosh ^2}y = \frac{1}{{1 – {{\tanh }^2}y}}.} 1– tanh 2 y = cosh 2 y 1 or cosh 2 y = 1– tanh 2 y 1 .
بنابراین،
( arctanh x ) ′ = cosh 2 y = 1 1 – tanh 2 y = 1 1 – tanh 2 ( arctanh x ) = 1 1 – x 2 ( ∣ x ∣ < 1 ) . {{\left( {\text{arctanh}\,x} \right)^\prime } }={ {\cosh ^2}y }={ \frac{1}{{1 – {{\tanh }^2}y}} } = {\frac{1}{{1 – {{\tanh }^2}\left( {\text{arctanh}\,x} \right)}} } = {\frac{1}{{1 – {x^2}}}\;\;\left( {\left| x \right| \lt 1} \right).} ( arctanh x ) ′ = cosh 2 y = 1– tanh 2 y 1 = 1– tanh 2 ( arctanh x ) 1 = 1– x 2 1 ( ∣ x ∣ < 1 ) .
به طریق مشابه، مشتق تابع y = f ( x ) = arccoth x y = f\left( x \right) = \text{arccoth}\,x y = f ( x ) = arccoth x
( arccoth x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( coth y ) ′ = 1 ( – 1 sinh 2 y ) = – sinh 2 y . {{\left( {\text{arccoth}\,x} \right)^\prime } }={ f’\left( x \right) } = {\frac{1}{{\varphi’\left( y \right)}} } = {\frac{1}{{{{\left( {\coth y} \right)}^\prime }}} } = {\frac{1}{{\left( { – \frac{1}{{{{\sinh }^2}y}}} \right)}} } = { – {\sinh ^2}y.} ( arccoth x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( coth y ) ′ 1 = ( – s i n h 2 y 1 ) 1 = – sinh 2 y .
با توجه به رابطه زیر:
coth 2 y – 1 = 1 sinh 2 y , ⇒ sinh 2 y = 1 coth 2 y – 1 , {{\coth ^2}y – 1 = \frac{1}{{{{\sinh }^2}y}},\;\;}\Rightarrow {{\sinh ^2}y = \frac{1}{{{{\coth }^2}y – 1}},} coth 2 y –1 = sinh 2 y 1 , ⇒ sinh 2 y = coth 2 y –1 1 ,
مشتق مورد نظر بهدست میآید:
( arccoth x ) ′ = – sinh 2 y = – 1 coth 2 y – 1 = – 1 coth 2 ( arccoth x ) – 1 = – 1 x 2 – 1 = 1 1 – x 2 ( ∣ x ∣ > 1 ) . {\left( {\text{arccoth}\,x} \right)^\prime } ={ – {\sinh ^2}y } = { – \frac{1}{{{{\coth }^2}y – 1}} } = { – \frac{1}{{{{\coth }^2}\left( {\text{arccoth}\,x} \right) – 1}} } = { – \frac{1}{{{x^2} – 1}} } = {\frac{1}{{1 – {x^2}}}\;\;}\kern-0.3pt{\left( {\left| x \right| \gt 1} \right).} ( arccoth x ) ′ = – sinh 2 y = – coth 2 y –1 1 = – coth 2 ( arccoth x ) –1 1 = – x 2 –1 1 = 1– x 2 1 ( ∣ x ∣ > 1 ) .
همانطور که میبینیم، مشتق توابع arctanh x \text{arctanh}\,x arctanh x arccoth x \text{arccoth}\,x arccoth x x x x
قید دامنه معکوس توابع تانژانت هیپربولیک و کتانژانت هیپربولیک، بهترتیب، مشابه برد توابع y = tanh x y = \tanh x y = tanh x y = coth x , y = \coth x, y = coth x ,
معکوس توابع سکانت هیپربولیک و کسکانت هیپربولیک را نیز میتوانیم مطابق روند بالا بهدست آوریم. برای مثال:
( arcsech x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( sech y ) ′ = 1 sech y tanh y . {{\left( {\text{arcsech}\,x} \right)^\prime } }={ f’\left( x \right) } = {\frac{1}{{\varphi’\left( y \right)}} } = {\frac{1}{{{{\left( {\text{sech}\,y} \right)}^\prime }}} } = {\frac{1}{{\text{sech}\,y\tanh y}}.} ( arcsech x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( sech y ) ′ 1 = sech y tanh y 1 .
عبارت tanh y \tanh y tanh y y > 0 y>0 y > 0 sech y \text{sech}\,y sech y
cosh 2 y – sinh 2 y = 1 , ⇒ 1 – tanh 2 y = 1 cosh 2 y = sech 2 y , ⇒ tanh 2 y = 1 – sech 2 y , ⇒ tanh y = 1 – sech 2 y . {{\cosh ^2}y – {\sinh ^2}y = 1,\;\;}\Rightarrow {1 – {\tanh ^2}y = \frac{1}{{{{\cosh }^2}y}} = {\text{sech}^2}y,\;\;}\Rightarrow {{\tanh ^2}y = 1 – {\text{sech}^2}y,\;\;}\Rightarrow {\tanh y = \sqrt {1 – {{\text{sech}}^2}y}.} cosh 2 y – sinh 2 y = 1 , ⇒ 1– tanh 2 y = cosh 2 y 1 = sech 2 y , ⇒ tanh 2 y = 1– sech 2 y , ⇒ tanh y = 1– sech 2 y .
و نتیجه بهصورت زیر خواهد بود:
( arcsech x ) ′ = – 1 sech y tanh y = – 1 x 1 – x 2 , x ∈ ( 0 , 1 ) . {{\left( {\text{arcsech}\,x} \right)^\prime } }={ – \frac{1}{{\text{sech}\,y \tanh y}} } = { – \frac{1}{{x\sqrt {1 – {x^2}} }},\;\;}\kern-0.3pt{x \in \left( {0,1} \right).} ( arcsech x ) ′ = – sech y tanh y 1 = – x 1– x 2 1 , x ∈ ( 0 , 1 ) .
به طریق مشابه، میتوانیم معکوس تابع کسکانت هیپربولیک را بهدست آوریم. فرض کنید y = f ( x ) = a r c c s c h x y = f\left( x \right)=\mathrm{arccsch}\, x y = f ( x ) = arccsch x x = φ ( y ) = c s c h y x = \varphi \left( y \right)=\mathrm{csch} \, y x = φ ( y ) = csch y x > 0 x>0 x > 0 y > 0 y>0 y > 0
( arccsch x ) ′ = f ’ ( x ) = 1 φ ’ ( y ) = 1 ( csch y ) ′ = – 1 csch y coth y . {{\left( {\text{arccsch}\,x} \right)^\prime } }={ f’\left( x \right) } = {\frac{1}{{\varphi’\left( y \right)}} } = {\frac{1}{{{{\left( {\text{csch}\,y} \right)}^\prime }}} } = { – \frac{1}{{\text{csch}\,y\coth y}}.} ( arccsch x ) ′ = f ’ ( x ) = φ ’ ( y ) 1 = ( csch y ) ′ 1 = – csch y coth y 1 .
از اتحادهای زیر استفاده میکنیم:
cosh 2 y – sinh 2 y = 1 , ⇒ coth 2 y – 1 = 1 sinh 2 y = csch 2 y , ⇒ coth 2 y = 1 + csch 2 y , ⇒ coth y = ± 1 + csch 2 y . {{\cosh ^2}y – {\sinh ^2}y = 1,\;\;}\Rightarrow {{\coth ^2}y – 1 = \frac{1}{{{{\sinh }^2}y}} = {\text{csch}^2}y,\;\;}\Rightarrow {{\coth ^2}y = 1 + {\text{csch}^2}y,\;\;}\Rightarrow {\coth y = \pm \sqrt {1 + {{\text{csch}}^2}y}.} cosh 2 y – sinh 2 y = 1 , ⇒ coth 2 y –1 = sinh 2 y 1 = csch 2 y , ⇒ coth 2 y = 1 + csch 2 y , ⇒ coth y = ± 1 + csch 2 y .
با فرض y > 0 y>0 y > 0 + + +
( arccsch x ) ′ = – 1 csch y coth y = – 1 x 1 + x 2 ( x > 0 ) . {{\left( {\text{arccsch}\,x} \right)^\prime } }={ – \frac{1}{{\text{csch}\,y \coth y}} } = { – \frac{1}{{x\sqrt {1 + {x^2}} }}\;\;}\kern-0.3pt{\left( {x \gt 0} \right).} ( arccsch x ) ′ = – csch y coth y 1 = – x 1 + x 2 1 ( x > 0 ) .
اکنون معکوس را در x < 0 x<0 x < 0 y < 0 y<0 y < 0
coth y = – 1 + csch 2 y ( y < 0 ) . {\coth y = – \sqrt {1 + {{\text{csch}}^2}y} \;\;}\kern-0.3pt{\left( {y \lt 0} \right).} coth y = – 1 + csch 2 y ( y < 0 ) .
در نتیجه، مشتق معکوس کسکانت هیپربولیک برای x < 0 x<0 x < 0
( arccsch x ) ′ = – 1 csch y coth y = 1 x 1 + x 2 ( x < 0 ) . {{\left( {\text{arccsch}\,x} \right)^\prime } }={ – \frac{1}{{\text{csch}\,y\coth y}} } = {\frac{1}{{x\sqrt {1 + {x^2}} }}\;\;}\kern-0.3pt{\left( {x \lt 0} \right).} ( arccsch x ) ′ = – csch y coth y 1 = x 1 + x 2 1 ( x < 0 ) .
حال اگر روابط مربوط به دو شاخه را با هم ترکیب کنیم، میتوانیم مشتق معکوس کسکانت هیپربولیک را بهفرم فشرده زیر بنویسیم:
( arccsch x ) ′ = – 1 ∣ x ∣ 1 + x 2 ( x ≠ 0 ) . {\left( {\text{arccsch}\,x} \right)^\prime } = { – \frac{1}{{\left| x \right|\sqrt {1 + {x^2}} }}\;\;}\kern-0.3pt{\left( {x \ne 0} \right).} ( arccsch x ) ′ = – ∣ x ∣ 1 + x 2 1 ( x = 0 ) .
برای محاسبه مشتق توابع هذلولوی و معکوس آنها، میتوان از جدول زیر کمک گرفت.
در پایان این مبحث، چند مثال را بررسی میکنیم.
مثال ۱
مشتق تابع y = coth 1 x y = \coth \frac{1}{x} y = coth x 1
حل:
y ’ ( x ) = ( coth 1 x ) ′ = – csch 2 ( 1 x ) ⋅ ( 1 x ) ′ = – csch 2 ( 1 x ) ⋅ ( – 1 x 2 ) = csch 2 ( 1 x ) x 2 . {y’\left( x \right) }={ {\left( {\coth \frac{1}{x}} \right)^\prime } } = { – {\text{csch}^2}\left( {\frac{1}{x}} \right) \cdot {\left( {\frac{1}{x}} \right)^\prime } } = { – {\text{csch}^2}\left( {\frac{1}{x}} \right) \cdot \left( { – \frac{1}{{{x^2}}}} \right) } = {\frac{{{{\text{csch}}^2}\left( {\frac{1}{x}} \right)}}{{{x^2}}}.} y ’ ( x ) = ( coth x 1 ) ′ = – csch 2 ( x 1 ) ⋅ ( x 1 ) ′ = – csch 2 ( x 1 ) ⋅ ( – x 2 1 ) = x 2 csch 2 ( x 1 ) .
مثال ۲
مشتق تابع y = ln ( sinh x ) , x > 0. {y = \ln \left( {\sinh x} \right),\;\;}\kern-0.3pt{x \gt 0.} y = ln ( sinh x ) , x > 0.
حل:
y ’ ( x ) = [ ln ( sinh x ) ] ′ = 1 sinh x ⋅ ( sinh x ) ′ = cosh x sinh x = tanh x . {y’\left( x \right) }={ {\left[ {\ln \left( {\sinh x} \right)} \right]^\prime } } = {\frac{1}{{\sinh x}} \cdot {\left( {\sinh x} \right)^\prime } } = {\frac{{\cosh x}}{{\sinh x}} = \tanh x.} y ’ ( x ) = [ ln ( sinh x ) ] ′ = sinh x 1 ⋅ ( sinh x ) ′ = sinh x cosh x = tanh x .
مثال ۳
مشتق تابع y = x sinh x – cosh x y = x\sinh x – \cosh x y = x sinh x – cosh x
حل:
$$\require{cancel}<br />
{y’\left( x \right) }={ {\left( {x\sinh x – \cosh x} \right)^\prime } }<br />
= {{\left( {x\sinh x} \right)^\prime } – {\left( {\cosh x} \right)^\prime } }<br />
= {x’\sinh x + x{\left( {\sinh x} \right)^\prime } }-{ {\left( {\cosh x} \right)^\prime } }\\<br />
= {1 \cdot \sinh x + x \cdot \cosh x }-{ \sinh x }<br />
= {\cancel{\sinh x} + x\cosh x – \cancel{\sinh x} }={ x\cosh x.}$$
مثال ۴
مشتق تابع y = arctanh ( cos x ) y = \text{arctanh}\left( {\cos x} \right) y = arctanh ( cos x )
حل:
y ’ ( x ) = [ arctanh ( cos x ) ] ′ = 1 1 – cos 2 x ⋅ ( cos x ) ′ = 1 sin 2 x ⋅ ( − sin x ) = – sin x sin 2 x = – 1 sin x = – csc x . {y’\left( x \right) }={ {\left[ {\text{arctanh}\left( {\cos x} \right)} \right]^\prime } } = {\frac{1}{{1 – {{\cos }^2}x}} \cdot {\left( {\cos x} \right)^\prime } } = {\frac{1}{{{{\sin }^2}x}} \cdot \left( { -\sin x} \right) } = { – \frac{{\cancel{\sin x}}}{{{{\sin }^{\cancel{2}}}x}} } = { – \frac{1}{{\sin x}} } = { – \csc x.} y ’ ( x ) = [ arctanh ( cos x ) ] ′ = 1– cos 2 x 1 ⋅ ( cos x ) ′ = sin 2 x 1 ⋅ ( − sin x ) = – sin 2 x sin x = – sin x 1 = – csc x .
دقت کنید باید دامنه این تابع را مشخص کنیم که بهصورت زیر است:
x ≠ π 2 + π n , n ∈ Z . x \ne {\large\frac{\pi }{2}\normalsize} + \pi n,\, n \in \mathbb{Z}. x = 2 π + πn , n ∈ Z .
اگر به موضوعات مرتبط با این مطلب علاقهمندید، پیشنهاد میکنیم آموزشهای زیر را نیز ببینید:
^^
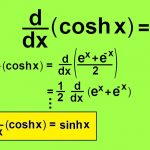
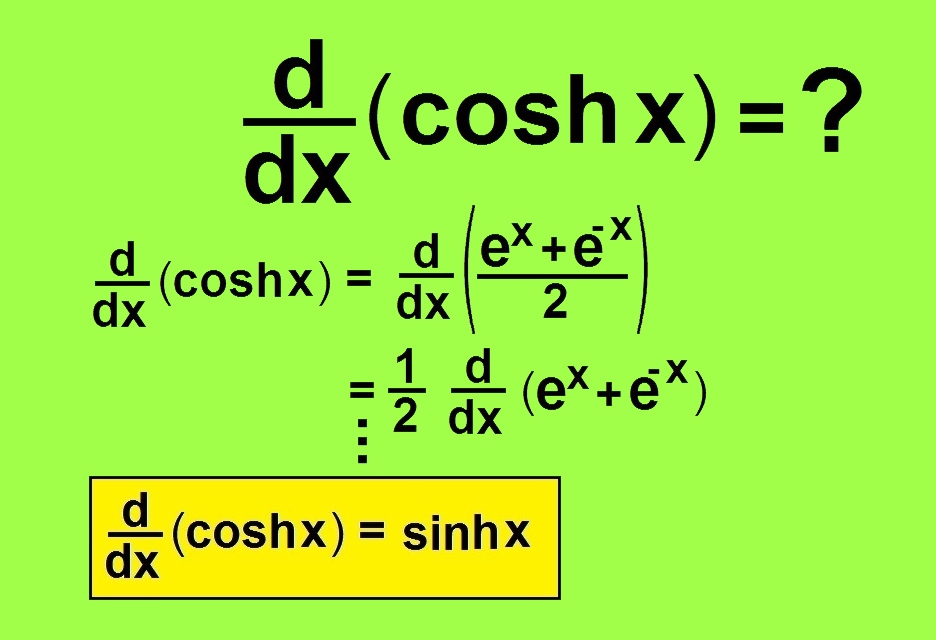














سلام آقای حمیدی یه سوال دارم:
دامنه توابع معکوس هذلولوی چگونه تعریف شده اند؟
سلام.
این توابع به صورت زیر هستند:
arsinhxarcoshxartanhxarcothxarsechxarcschx=ln(x+x2+1)=ln(x+x2–1)=21ln(1−x1+x)=21ln(x−1x+1)=ln(x1+x21−1)=ln(x1+1−x2)=ln(x1+x21+1)=ln(x1+1+x2)
دامنه این توابع xهایی است که به ازای آنها آرگومان ln و عبارت زیر رادیکال مثبت باشد.
سالم و موفق باشید.