مساحت مثلث متساوی الاضلاع — حل تمرین و مثال های متنوع

مساحت مثلث متساوی الاضلاع برابر قاعده ضربدر ارتفاع تقسیم بر دو است. البته به دلیل برابر بودن اندازه ضلع‌های مثلث متساوی الاضلاع، امکان محاسبه مساحت آن با استفاده از اندازه یک ضلع یا اندازه یک ارتفاع نیز وجود دارد. در این مقاله از مجله فرادرس، به معرفی روش‌های محاسبه مساحت مثلث متساوی الاضلاع به همراه حل چندین مثال متنوع می‌پردازیم.

مثلث چیست ؟

مثلث، یکی از اشکال پایه هندسی است. این شکل از سه ضلع (قاعده)، سه ارتفاع، سه زاویه داخلی و سه زاویه خارجی تشکیل می‌شود. تصویر زیر، یکی از انواع مثلث را نمایش می‌دهد.

انواع مثلث چه هستند؟

مثلث‌، دارای انواع مختلف است. این شکل هندسی، بر اساس اندازه زاویه و ضلع، به انواع زیر تقسیم می‌شود:

• انواع مثلث بر اساس اندازه زاویه داخلی
  • مثلث با زاویه بسته یا حاده (یک زاویه بزرگ‌تر از 90 درجه)
  • مثلث با زاویه 90 درجه یا قائم الزاویه
  • مثلث با زاویه باز یا منفرجه (سه زاویه کوچک‌تر از 90 درجه)
• انواع مثلث بر اساس اندازه ضلع
  • مثلث مختلف الاضلاع (سه ضلع نابرابر)
  • مثلث متساوی الساقین (دو ضلع هم اندازه)
  • مثلث متساوی الاضلاع (سه ضلع هم اندازه)

مساحت مثلث چیست و چگونه به دست می آید ؟

مساحت مثلث، مقدار سطح درون ضلع‌های این شکل هندسی است. در حالت کلی، مساحت مثلث با استفاده از فرمول «قاعده ضربدر ارتفاع تقسیم بر دو» به دست می‌آید.

البته در صورت مشخص بودن اندازه سه ضلع، از روش هرون و در صورت داشتن حداقل یک ضلع و دو زاویه، از روش سینوس به منظور تعیین مساحت استفاده می‌شود.

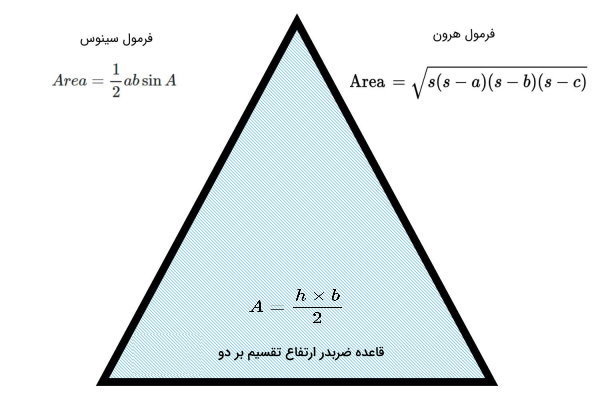
سه روش معرفی شده، برای تمام مثلث‌ها قابل استفاده هستند. در حالت‌های خاص مانند قائم الزاویه، متساوی الساقین یا متساوی الاضلاع بودن مثلث، معمولا فرمول‌های مخصوص به آن حالت برای محاسبه مساحت مورد استفاده قرار می‌گیرند.

مثال 1: محاسبه مساحت مثلث

مساحت یک مثلث متساوی الاضلاع با ارتفاع 7 سانتی‌متر و قاعده 8 سانتی‌متر را حساب کنید.

در صورت مشخص بودن قاعده و ارتفاع نظیر، می‌توان مساحت هر مثلثی را محاسبه کرد. به این منظور، کافی است فرمول زیر را نوشت و اندازه‌های معلوم را درون آن قرار داد:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

۲ ÷ (7 $$\times$$ 8) = مساحت مثلث

۲ ÷ (56) = مساحت مثلث

28 = مساحت مثلث

در نتیجه، مساحت مثلث متساوی الاضلاع برابر 28 سانتی‌متر مربع است.

مثلث متساوی الاضلاع چیست ؟

مثلث متساوی الاضلاع، یکی از انواع مثلث است که تمام ضلع‌های آن با هم برابر هستند. علاوه بر ضلع‌ها یا قاعده‌ها، ارتفاع‌ها، زوایای داخلی و زوایای خارجی این نوع مثلث نیز هم اندازه هستند. تصویر زیر، اجزای اصلی یک مثلث متساوی الاضلاع را نمایش می‌دهد.

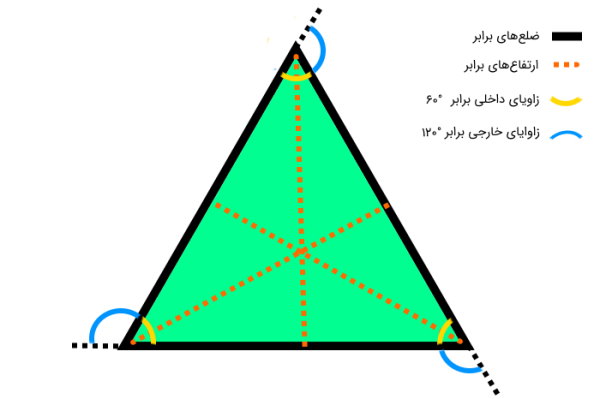
به دلیل برابر بودن اندازه‌های اجزای مثلث متساوی الاضلاع، فرمول‌های مورد استفاده برای محاسبه مساحت این مثلث با فرمول‌های کلی تفاوت دارند.

مساحت مثلث متساوی الاضلاع چگونه بدست می  آید ؟

مساحت مثلث متساوی الاضلاع با استفاده از اندازه یکی از قاعده‌ها یا اندازه یکی از ارتفاع‌های آن به دست می‌آید.

البته در صورت معلوم محیط مثلث متساوی الاضلاع معلوم نیز می‌توان مساحت این مثلث را تعیین کرد.

فرمول مساحت مثلث با ارتفاع و قاعده

فرمول مساحت مثلث متساوی الاضلاع با ارتفاع و قاعده برابر است با:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$
A = \frac {h \times b } { 2 }
$$

• A: مساحت مثلث متساوی الاضلاع
• h: اندازه ارتفاع مثلث متساوی الاضلاع
• b: اندازه قاعده یا ضلع مثلث متساوی الاضلاع

مثال 2: محاسبه مساحت مثلث با ارتفاع و قاعده

اندازه قاعده و ارتفاع یک مثلث متساوی الاضلاع، به ترتیب برابر 15 و 13 است. مساحت این مثلث را حساب کنید.

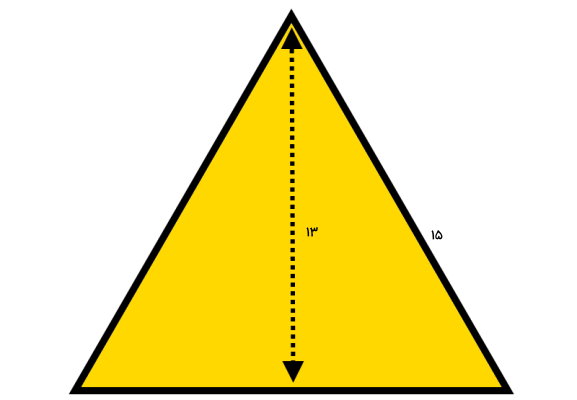
بر اساس فرمول مساحت مثلث متساوی الاضلاع با ارتفاع و قاعده، داریم:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$
A = \frac {h \times b } { 2 }
$$

• A: مساحت مثلث
• h: ارتفاع مثلث برابر 13
• b: قاعده مثلث برابر 15

اندازه‌های معلوم را در رابطه بالا قرار می‌دهیم:

۲ ÷ (13 $$\times$$ 15) = مساحت مثلث

۲ ÷ (195) = مساحت مثلث

97.5 = مساحت مثلث

مساحت مثلث متساوی الاضلاع برابر 97/5 است. در حالت کلی، مساحت تمام مثلث‌ها با استفاده از فرمول بالا به دست می‌آید. با این وجود، در مثلث‌های خاص نظیر مثلث متساوی الاضلاع، امکان محاسبه مساحت با یکی از اندازه‌های بالا نیز وجود دارد.

فرمول مساحت مثلث متساوی الاضلاع بدون ارتفاع

مساحت مثلث متساوی الاضلاع با یک ضلع (بدون ارتفاع) به صورت زیر نوشته می‌شود:

$$
A = \frac { \sqrt {3} } {4} a^2
$$

• A: مساحت مثلث متساوی الاضلاع
• a: اندازه ضلع مثلث متساوی الاضلاع

مثال 3: تعیین مساحت مثلث بدون ارتفاع

مساحت مثلثی با سه ضلع برابر به اندازه 2 چقدر است؟

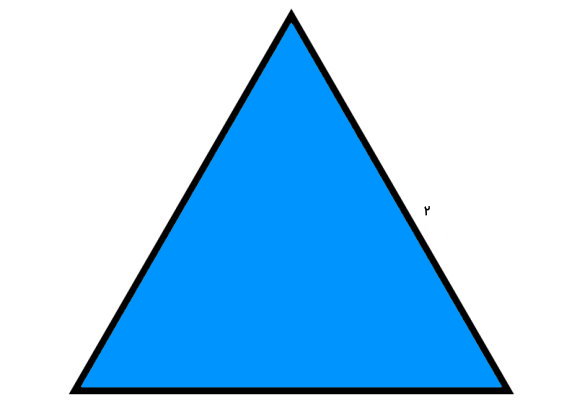
به دلیل هم اندازه بودن اضلاع، مثلث مورد سوال از نوع متساوی الاضلاع است. مساحت این نوع مثلث، از فرمول زیر به دست می‌آید:

$$
A = \frac { \sqrt {3} } {4} a^2
$$

• A: مساحت
• a: اندازه ضلع برابر 2

اندازه ضلع را درون فرمول بالا قرار می‌دهیم:

$$
A = \frac { \sqrt {3} } {4} \times 2^2
$$

$$
A = \frac { \sqrt {3} } {4} \times 4
$$

$$
A = \sqrt {3}
$$

در نتیجه، مساحت مثلث برابر با $$\sqrt {3}$$ است.

فرمول مساحت مثلث متساوی الاضلاع بدون قاعده

فرمول مساحت مثلث متساوی الاضلاع با ارتفاع (بدون ضلع یا بدون قاعده) به صورت زیر نوشته می‌شود:

$$
A=\frac{\sqrt{3}}{3} h^{2}
$$

• A: مساحت مثلث متساوی الاضلاع
• h: اندازه ارتفاع مثلث متساوی الاضلاع

مثال 4: تعیین ارتفاع مثلث از روی مساحت

اگر مساحت یک مثلث برابر $$12 \sqrt {3}$$ و هر سه ارتفاع آن با هم برابر باشد، اندازه ارتفاع چقدر خواهد بود؟

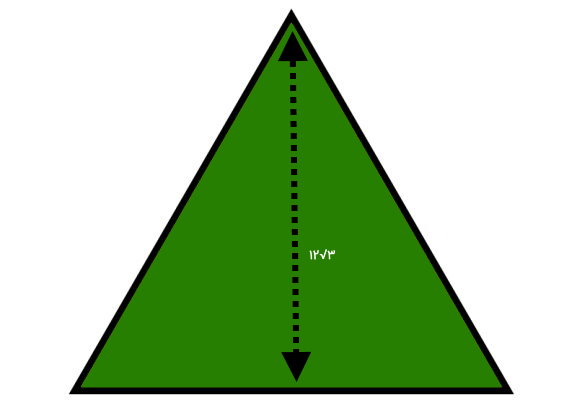
به دلیل برابر بودن اندازه ارتفاع‌ها، مثلث بالا، قطعا از نوع متساوی الاضلاع است. مساحت این مثلث بر اساس ارتفاع، از فرمول زیر به دست می‌آید:

$$
A=\frac{\sqrt{3}}{3} h^{2}
$$

• A: مساحت مثلث برابر $$12 \sqrt {3}$$
• h: ارتفاع

از آنجایی که در فرمول بالا، فقط ارتفاع مجهول است، با قرار دادن اندازه مساحت در آن می‌توانیم ارتفاع را تعیین کنیم:

$$
12 \sqrt {3}=\frac{\sqrt{3}}{3} h^{2}
$$

$$
\frac {12 \sqrt {3} \times 3} { \sqrt {3}} = h^{2}
$$

$$
12 \times 3 = h^{2}
$$

$$
36 = h^{2}
$$

$$
\sqrt {36} = h
$$

$$
6 = h
$$

در نتیجه، ارتفاع مثلث برابر 6 خواهد بود.

فرمول مساحت مثلث متساوی الاضلاع با محیط

فرمول مساحت مثلث متساوی الاضلاع بر اساس محیط آن به صورت زیر نوشته می‌شود:

$$
A=\sqrt{3} \frac{P^{2}}{36}
$$

• A: مساحت مثلث متساوی الاضلاع
• P: محیط مثلث متساوی الاضلاع

البته به خاطر داشته باشید که فرمول محیط مثلث متساوی الاضلاع عبارت است از:

$$
P = 3 a
$$

• P: محیط مثلث متساوی الاضلاع
• a: اندازه ضلع مثلث متساوی الاضلاع

به این ترتیب، در صورت داشتن محیط مثلث، می‌توان اندازه ضلع آن را از رابطه بالا محاسبه کرده و سپس مساحت را به دست آورد.

فرمول مساحت مثلث متساوی الاضلاع با سینوس

فرمول مساحت مثلث متساوی الاضلاع با سینوس، به صورت زیر نوشته می‌شود:

$$
Area=\frac{1}{2} a b \sin C
$$

• Area: مساحت مثلث متساوی الاضلاع
• a: اندازه یکی از اضلاع مثلث
• b: اندازه یکی دیگر از اضلاع مثلث
• C: زاویه بین دو ضلع a و b

از آنجایی که اندازه تمام ضلع‌های مثلث متساوی الاضلاع با هم برابر هستند، می‌توان ضلع b را با a نمایش داد. به علاوه تمام زوایای مثلث متساوی الاضلاع برابر 60 درجه است. به این ترتیب، داریم:

$$
Area=\frac{1}{2} \times a \times a \times \sin 60°
$$

سینوس زاویه 60 درجه برابر $$\frac { \sqrt {3} } {2}$$ است. بنابراین:

$$
Area=\frac{1}{2} \times a^2 \times \frac { \sqrt {3} } {2}
$$

$$
Area= a^2 \times \frac { \sqrt {3} } {4}
$$

این فرمول، همان فرمول مساحت مثلث متساوی الاضلاع با یک ضلع است.

محاسبه آنلاین مساحت مثلث متساوی الاضلاع

سایت‌های اینترنتی مختلفی برای محاسبه آنلاین مساحت انواع مثلث وجود دارند. از بهترین ابزارهای آنلاین محاسبه مساحت مثلث متساوی الاضلاع می‌توان به موارد زیر اشاره کرد:

• موتور جستجوی گوگل
• Calculator.net (+)
• Omni Calculator (+)

هر یک از سایت‌های بالا، امکانات متنوعی را در اختیار کاربران قرار می‌دهند. از بین موارد معرفی شده، کار کردن با ابزار محاسباتی گوگل ساده‌تر و قابل دسترس‌تر است.

اگر در موتور جستجوی گوگل، عبارت فارسی «مثلث متساوی الاضلاع» یا عبارت انگلیسی «equilateral triangle» را جستجو کنید، کادر زیر در ابتدای صفحه نتایج به نمایش در می‌آید.

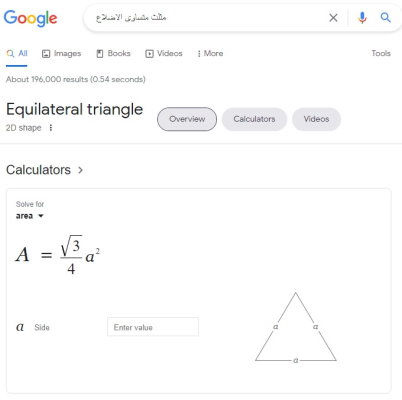
ماشین حساب بالا، امکان محاسبه آنلاین مساحت مثلث متساوی الاضلاع بر حسب اندازه یکی از ضلع‌ها را فراهم می‌کند. به عنوان مثال، با وارد کردن عدد 30 درون کادر مقابل «a Side»، مساحت مثلث محاسبه و روند حل آن نمایش داده می‌شود.

حل مثال های مساحت متساوی الاضلاع

در این بخش، به حل چند مثال بیشتر برای یادگیری بهتر روش‌های مختلف محاسبه مساحت مثلث متساوی الاضلاع می‌پردازیم.

مثال 5: محاسبه مساحت مثلث با قاعده و ارتفاع

مساحت یک مثلث متساوی الاضلاع به ارتفاع 26 و ضلع 30 را با فرمول کلی مساحت مثلث‌ها و فرمول‌های مخصوص مثلث متساوی الاضلاع محاسبه کنید.

مساحت تمام مثلث‌ها از رابطه زیر به دست می‌آید:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

اندازه‌های داده شده در سوال را درون رابطه بالا قرار می‌دهیم:

۲ ÷ (26 $$\times$$ 30) = مساحت مثلث

۲ ÷ (780) = مساحت مثلث

390 = مساحت مثلث

بر اساس فرمول مخصوص مساحت مثلث متساوی الاضلاع با قاعده، داریم:

$$
A = \frac { \sqrt {3} } {4} a^2
$$

• A: مساحت مثلث
• a: اندازه ضلع مثلث برابر 6

$$
A = \frac { \sqrt {3} } {4} \times 30^2
$$

$$
A = \frac { \sqrt {3} } {4} \times 900
$$

$$
A = 225\sqrt {3}
$$

$$
A \approx 390
$$

فرمول مخصوص مساحت مثلث متساوی الاضلاع با ارتفاع، به صورت زیر نوشته می‌شود:

$$
A=\frac{\sqrt{3}}{3} h^{2}
$$

• A: مساحت
• h: اندازه ارتفاع برابر 26

$$
A=\frac{\sqrt{3}}{3} \times 26^{2}
$$

$$
A=\frac{\sqrt{3}}{3} \times 676
$$

$$
A \approx 225\sqrt {3}
$$

$$
A \approx 390
$$

مثال 6: محاسبه اندازه ضلع مثلث متساوی الاضلاع

مساحت یک مثلث متساوی الاضلاع برابر 6.8 متر مربع است. اندازه قاعده این مثلث را حساب کنید. ($$\sqrt {3}$$ را برابر 1/7 در نظر بگیرید.)

فرمول محاسبه مساحت مثلث متساوی الاضلاع را می‌نویسیم:

$$
A = \frac { \sqrt {3} } {4} a^2
$$

• A: مساحت مثلث برابر 13/6 متر مربع
• a: ضلع مثلث

مساحت معلوم را درون فرمول قرار می‌دهیم:

$$
6.8 = \frac { 1/7 } {4} a^2
$$

$$
\frac {6.8 \times 4} {1/7} = a^2
$$

$$
4 \times 4 = a^2
$$

$$
16 = a^2
$$

$$
\sqrt {16} = a
$$

$$
4 = a
$$

اندازه ضلع مثلث برابر 4 است.

مثال 7: مساحت قسمت رنگی

تصویر زیر، یک مثلث متساوی الاضلاع را درون یک مربع نمایش می‌دهد. مساحت بخش رنگی این شکل ترکیبی را پیدا کنید. ($$\sqrt {3}$$ را برابر 1/7 در نظر بگیرید.)

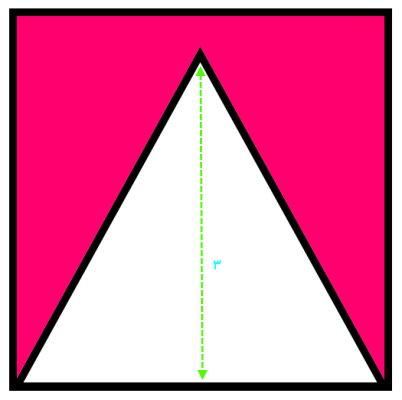
مساحت بخش هاشور خورده در تصویر بالا برابر است با:

مساحت مثلث - مساحت مربع = مساحت قسمت رنگی

برای مثلث، اندازه ارتفاع 3 را داریم. به این ترتیب، فرمول زیر را برای محاسبه مساحت آن می‌نویسیم:

$$
A_t=\frac{\sqrt{3}}{3} h^{2}
$$

• A_t: مساحت مثلث متساوی الاضلاع
• h: اندازه ارتفاع مثلث برابر 3

$$
A_t=\frac{\sqrt{3}}{3} \times 3^{2}
$$

$$
A_t=\frac{\sqrt{3}}{3} \times 9
$$

$$
A_t=3 \sqrt{3}
$$

در نتیجه مساحت مثلث متساوی الاضلاع برابر $$3 \sqrt {3}$$ است. برای محاسبه مساحت مربع، به اندازه ضلع آن نیاز داریم. قاعده مثلث متساوی الاضلاع، بر روی ضلع مربع منطبق شده است. به این ترتیب، با پیدا کردن اندازه قاعده مثلث، می‌توانیم یکی از ضلع‌های مربع و مساحت آن را حساب کنیم. این کار با نوشتن فرمول مساحت مثلث متساوی الاضلاع بر حسب قاعده و ارتفاع انجام می‌شود:

۲ ÷ (ارتفاع $$\times$$ قاعده) = مساحت مثلث

$$
A_t = \frac {h \times b } { 2 }
$$

• A_t: مساحت مثلث $$3 \sqrt {3}$$
• h: اندازه ارتفاع مثلث برابر 3
• b: اندازه قاعده یا ضلع مثلث

$$
3 \sqrt {3} = \frac {3 \times b } { 2 }
$$

$$
\frac {2 \times 3 \sqrt {3}} {3} = b
$$

$$
2 \sqrt {3} = b
$$

بنابراین، اندازه قاعده مثلث یا همان ضلع مربع برابر با $$2 \sqrt {3}$$ است. به این ترتیب، مساحت مربع برابر خواهد بود با:

خودش $$\times$$ یک ضلع = مساحت مربع

$$
A_s = a \times a
$$

• A_s: مساحت مربع
• a: اندازه ضلع

$$
A_s = 2 \sqrt {3} \times 2 \sqrt {3}
$$

$$
A_s = 4 (\sqrt {3} \times \sqrt {3})
$$

$$
A_s = 4 (3)
$$

$$
A_s = 12
$$

با مشخص شدن مساحت مربع (12)، مساحت مثلث را از آن کم می‌کنیم تا مساحت قسمت رنگی به دست بیاید:

مساحت مثلث - مساحت مربع = مساحت قسمت رنگی

$$12- 3 \sqrt {3}$$ = مساحت قسمت رنگی

بر اساس فرض مسئله، $$\sqrt {3}$$ را برابر 1/7 در نظر می‌گیریم:

$$12 - (3 \times 1.7)$$ = مساحت قسمت رنگی

$$12 - (5.1)$$ = مساحت قسمت رنگی

$$6.9$$ = مساحت قسمت رنگی

در نتیجه، مساحت قسمت رنگی شکل برابر 6/9 است.

مثال 8: محاسبه مساحت مثلث متساوی الاضلاع محاط در دایره

اگر مثلث نمایش داده شده در تصویر زیر، متساوی الاضلاع باشد، مساحت قسمت رنگی دایره چقدر خواهد بود؟ (عدد پی را برابر 3 و رادیکال 3 را برابر 1/7 در نظر بگیرید.)

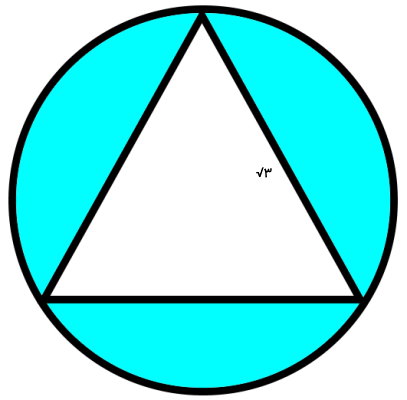
برای حل این مثال، باید با فرمول مساحت دایره و رابطه بین ضلع مثلث متساوی الساقین با شعاع دایره آشنا باشید. مساحت قسمت رنگی برابر است با:

مساحت مثلث - مساحت دایره = مساحت قسمت رنگی

به دلیل متساوی الاضلاع بودن مثلث، مساحت آن از رابطه زیر محاسبه می‌شود:

$$
A_t = \frac { \sqrt {3} } {4} a^2
$$

• A_t: مساحت مثلث
• a: اندازه ضلع مثلث متساوی الاضلاع برابر با $$\sqrt{3}$$

$$
A_t = \frac { \sqrt {3} } {4} \times (\sqrt {3})^2
$$

$$
A_t = \frac { \sqrt {3} } {4} \times 3
$$

$$
A_t = \frac { 1/7 \times 3 } {4}
$$

$$
A_t = \frac { 5.1 } {4}
$$

$$
A_t = 1.275
$$

مساحت مثلث متساوی الساقین برابر 1/275 است. مساحت دایره، از فرمول زیر به دست می‌آید:

$$
A_c = \pi r^ { 2 }
$$

• A_c: مساحت دایره
• π: عدد ثابت پی برابر 3 (بر اساس فرض مسئله)
• r: شعاع دایره

همان طور که مشاهده می‌کنید، برای محاسبه مساحت دایره به شعاع آن نیاز داریم. در اینجا فقط اندازه ضلع مثلث داده شده است. رابطه بین اندازه ضلع مثلث متساوی الساقین محاطی با شعاع دایره محیط بر آن نیز به صورت زیر نوشته می‌شود:

$$
r=a \frac{\sqrt{3}}{3}
$$

• r: شعاع دایره محیطی
• a: اندازه ضلع مثلث متساوی الاضلاع برابر با $$\sqrt{3}$$

اندازه ضلع را درون رابطه بالا قرار می‌دهیم:

$$
r= \sqrt {3} \times \frac{\sqrt{3}}{3}
$$

$$
r= \frac{3}{3}
$$

$$
r= 1
$$

اکنون می‌توان مساحت دایره را نیز تعیین کنیم:

$$
A_c = \pi r^ { 2 }
$$

$$
A_c = 3 \times 1^ { 2 }
$$

$$
A_c = 3
$$

با تعیین مساحت دایره و مثلث، مساحت قسمت رنگی به صورت زیر به دست می‌آید:

مساحت مثلث - مساحت دایره = مساحت قسمت رنگی

1/275 - 3 = مساحت قسمت رنگی

1/725 = مساحت قسمت رنگی

مساحت قسمت رنگی دایره برابر 1/725 است.

مثال 9: محاسبه مساحت مثلث متساوی الساقین محیط بر دایره

یک دایره را درون مثلث متساوی الاضلاع زیر محاط کرده‌ایم. با توجه به اطلاعات نمایش داده شده، مساحت قسمت رنگی مثلث را حساب کنید. (عدد پی را برابر 3 و رادیکال 3 را برابر 1/7 در نظر بگیرید.)

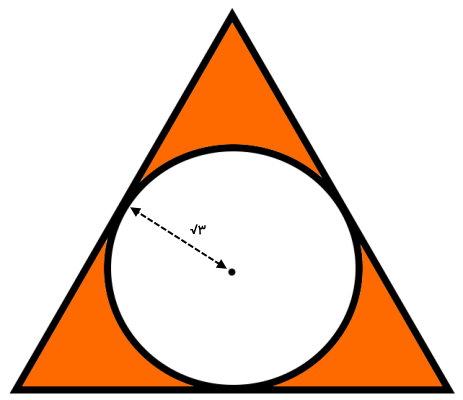
محاسبه قسمت رنگی مثلث، به صورت زیر انجام می‌شود:

مساحت دایره - مساحت مثلث = مساحت قسمت رنگی

بر اساس تصویر بالا، شعاع دایره برابر با $$\sqrt{3}$$ است. از این اندازه برای محاسبه مساحت دایره استفاده می‌کنیم:

$$
A_c = \pi r^ { 2 }
$$

• A_c: مساحت دایره
• π: عدد ثابت پی برابر 3 (بر اساس فرض مسئله)
• r: شعاع دایره برابر با $$\sqrt{3}$$

$$
A_c = 3 \times (\sqrt {3})^ { 2 }
$$

$$
A_c = 3 \times 3
$$

$$
A_c = 9
$$

برای محاسبه مساحت مثلث متساوی الاضلاع، به اندازه یکی از ضلع‌های آن نیاز داریم. رابطه بین ضلع مثلث متساوی الاضلاع با شعاع دایره محاط در آن برابر است با:

$$
\mathrm{r}=a \frac{\sqrt{3}}{6}
$$

• r: شعاع دایره برابر با $$\sqrt{3}$$
• a: ضلع مثلث متساوی الاضلاع محیط بر دایره

$$
\sqrt {3}=a \frac{\sqrt{3}}{6}
$$

$$
\frac{6 \times \sqrt {3}} {\sqrt{3}}=a
$$

$$
6=a
$$

به این ترتیب، اندازه یکی از ضلع‌های مثلث برابر 6 است. از این اندازه برای محاسبه مساحت مثلث متساوی الاضلاع بر حسب قاعده استفاده می‌کنیم:

$$
A_t = \frac { \sqrt {3} } {4} a^2
$$

• A_t: مساحت مثلث
• a:اندازه قاعده یا ضلع مثلث برابر 6

$$
A_t = \frac { \sqrt {3} } {4} \times 6^2
$$

$$
A_t = \frac { \sqrt {3} } {4} \times 36
$$

$$
A_t = 9 \sqrt {3}
$$

$$
A_t = 9 \times 1.7
$$

$$
A_t = 15.3
$$

مساحت مثلث برابر 15/3 است. با کم کردن مساحت دایره (9) از این مقدار، مساحت قسمت رنگی شکل به دست می‌آید:

مساحت دایره - مساحت مثلث = مساحت قسمت رنگی

9 - 15/3 = مساحت قسمت رنگی

6/3 = مساحت قسمت رنگی

مثال 10: محاسبه مساحت مثلث از روی محیط

مساحت مثلث متساوی الاضلاع به محیط P چقدر است؟

فرمول مساحت مثلث متساوی الاضلاع به صورت زیر نوشته می‌شود:

$$
A = \frac { \sqrt {3} } {4} a^2
$$

• A: مساحت
• a: اندازه ضلع

فرمول بالا، مساحت مثلث متساوی الاضلاع را بر حسب ضلع a محاسبه می‌کند. در صورتی که در صورت سوال، محیط P داده شده است. به این ترتیب، برای شروع حل مسئله، ابتدا فرمول محیط مثلث متساوی الاضلاع را می‌نویسیم:

$$
P = 3 a
$$

• P: محیط مثلث
• a: اندازه ضلع

سپس، فرمول بالا را بر حسب a بازنویسی می‌کنیم:

$$
a = \frac {P} {3}
$$

بنابراین، اندازه ضلع مثلث متساوی الساقین برابر $$\frac {P} {3}$$ است. این مقدار را به جای ضلع a درون فرمول جایگذاری قرار می‌دهیم:

$$
A = \frac { \sqrt {3} } {4} ( \frac {P} {3} )^2
$$

$$
A = \frac { \sqrt {3} } {4} \times \frac {P^2} {9}
$$

$$
A = \frac { P^2 \times \sqrt {3} } {36}
$$

نتیجه حل رابطه بالا، همان فرمول مخصوص محاسبه مساحت مثلث متساوی الاضلاع بر حسب محیط است.

مثال 11: محاسبه مساحت مثلث متساوی الاضلاع به روش هرون

مساحت مثلث متساوی الاضلاع به ضلع a را توسط روش هرون محاسبه کنید.

محاسبه مساحت مثلث با سه ضلع یا روش هرون، در مواقعی مورد استفاده قرار می‌گیرد که سه ضلع مثلث معلوم باشند. فرمول هرون به صورت زیر نوشته می‌شود:

$$
A=\sqrt{s(s-a)(s-b)(s-c)}
$$

• A: مساحت
• s: نصف محیط مثلث
• a: طول ضلع اول
• b: طول ضلع دوم
• c: طول ضلع سوم

نصف محیط مثلث، عبارت است از:

$$
s=\frac{a+b+c}{2}
$$

از آنجایی که اندازه تمام ضلع‌های مثلث برابر a هستند، فرمول مساحت و نصف محیط به شکل زیر در می‌آیند:

$$
A=\sqrt{s(s-a)(s-a)(s-a)}
$$

$$
s = \frac { a + a + a } {2} = \frac { 3a }{2}
$$

در نتیجه:

$$
A = \sqrt { \frac { 3a }{2} ( \frac { 3a }{2} - a ) ( \frac { 3a }{2} - a ) ( \frac { 3a }{2} - a ) }
$$

$$
A = \sqrt { \frac { 3a }{2} ( \frac { a }{2} ) ( \frac { a }{2} ) ( \frac { a }{2} ) }
$$

$$
A = \sqrt { \frac { 3a^4 }{16} }
$$

$$
A = \frac {\sqrt {3}} {4}a^2
$$

همان طور که مشاهده می‌کنید، نتیجه حل مساحت مثلث متساوی الاضلاع با سه ضلع، همان فرمول مساحت مثلث متساوی الاضلاع با ضلع است.

سوالات متداول در رابطه با مثلث متساوی الاضلاع

در این مطلب از مجله فرادرس با مثلث متساوی‌الاضلاع و محاسبه محیط و مساحت آن آشنا شدیم. در این بخش، به چند سوال پرتکرار در رابطه با ویژگی‌های مثلث‌های متساوی الاضلاع پاسخ می‌دهیم. پاسخ این سوالات می‌تواند شما را در یادگیری مبحث مساحت مثلث متساوی الاضلاع کمک کند.

تعریف مثلث متساوی الاضلاع چیست؟

مثلثی که سه ضلع آن برابرند، مثلث متساوی الاضلاع نام دارد.

محیط مثلث متساوی الاضلاع چگونه بدست می‌آید؟

محیط مثلث متساوی الاضلاع از ضرب اندازه‌ی یک ضلع در عدد 3 به دست می‌آید. به عبارت دیگر، محیط مثلث متساوی الاضلاع، سه برابر اندازه یک ضلع آن است.

زاویه هر راس مثلث متساوی الاضلاع چقدر است؟

زاویه هر راس مثلث متساوی الاضلاع برابر 60 درجه است.

مساحت مثلث متساوی الاضلاع چگونه حساب می‌شود؟

مساحت مثلث متساوی الاضلاع با استفاده از «قاعده ضربدر ارتفاع تقسیم بر دو» حساب می‌شود.

برای محاسبه مساحت مثلث متساوی الاضلاع به چه اندازه‌هایی نیاز است؟

برای محاسبه مساحت مثلث متساوی الاضلاع، داشتن اندازه یک ضلع کافی است. البته امکان محاسبه این مساحت با اندازه یک ارتفاع نیز وجود دارد.