مدل سازی مبدل های سوئیچینگ — از صفر تا صد

در آموزش‌های قبلی مجله فرادرس، با برخی از مبدل‌های الکترونیک قدرت، ار قبیل مبدل‌های DC به DC و یکسوسازها آشنا شدیم. در این آموزش درباره مدل سازی مبدل ها در الکترونیک قدرت بحث خواهیم کرد.

مدل سازی مبدل ها

مدل‌سازی هر پدیده یا فرایند بر اساس مشاهدات آن است و تقریبی از آن را ارائه می‌کند که باید به‌ اندازه کافی جامع بوده و مهم‌ترین ویژگی‌های فرایند را با توجه به کاربردهای مورد نظر در بر داشته باشد. مدل‌سازی پدیده مورد مطالعه باید به‌ گونه‌ای قابل تعمیم باشد که بتوان ویژگی‌های مشترک سایر پدیده‌های مشابه را از آن استخراج کرد.

فیلم آموزش الکترونیک قدرت 1 – جامع و با نکات کاربردی در فرادرس

کلیک کنید

به‌ طور کلی دو رویکرد اصلی در مدل‌سازی وجود دارد: یکی استفاده از مدل جعبه‌ سیاه بر اساس مشاهده رفتار فرایند از روی پاسخ آن به بعضی از سیگنال‌های ورودی معلوم و دیگری بر اساس اطلاعات معلوم درباره سیستمی که باید مدل شود (یعنی توصیف بر اساس قوانین رفتاری). روش دوم نه‌تنها در مدل‌سازی فرایندهای فیزیکی، بلکه در سیستم‌های زیست‌شناختی، اقتصادی و یا حتی اجتماعی نیز به کار می‌رود. ترکیب این دو روش نیز، به‌نام مدل جعبه‌ خاکستری وجود دارد.

تمرکز این آموزش روی مدل‌سازی مبدل‌های الکترونیک قدرت با استفاده از رویکرد «اطلاعات» است؛ بدین معنی که توصیف مدل با استفاده از دانش فیزیکی موجود درباره مبدل بیان می‌شود. به‌ طور کلی، دانش فیزیکی درباره سیستم به توصیف ریاضی قوانین پایستگی جرم و انرژی منجر می‌شود. بر این‌ اساس، تغییرات انرژی ذخیره‌ شده در سیستم نیز با متغیرهای حالت توصیف می‌شود. در مورد مبدل‌های الکترونیک قدرت، قوانین کیرشهف متناظر با مدار مبدل، قوانین اهم برای بارهای مختلف و در نهایت، وضعیت کلیدهای حالت جامد مختلف، اطلاعات سیستم را شکل می‌دهند.

برای شبیه‌سازی، نرم‌افزارهای بسیار دقیق و قابل اطمینانی وجود دارند که با استفاده از آن‌ها می‌توان رفتار حوزه زمان مبدل‌های الکترونیک قدرت را بررسی کرد (مانند نرم‌افزارهای سابر، اسپایس و متلب). هرچند نتایج این برنامه‌ها قابل تعمیم نیست؛ برای مثال حتی اگر این نرم‌افزارها شکل موج‌های زمانی مختلفی از متغیرهای درونی نشان دهند، اما اطلاعات مستقیمی درباره مُدهای مبدل ارائه نمی‌کنند؛ در نتیجه برای به دست آوردن یک مدل به منظور اهداف کنترل، نمی‌توان از بسته‌های نرم‌افزاری - حداقل به صورت مستقیم - استفاده کرد. قطعاً می‌توان یک مبدل الکترونیک قدرت را بر اساس نِمُو متغیرهای ورودی-خروجی به‌ دست‌ آمده از شبیه‌سازی شناسایی کرد و مدل حوزه فرکانس مناسب را به دست آورد، اما با توجه به اینکه تقریباً همه مبدل‌های الکترونیک قدرت، سیستم‌هایی غیرخطی یا خطی تغییر پذیر با زمان هستند و هر مدل ورودی-خروجی خطی به نقطه کار بستگی دارد، اعتبار اطلاعات آن محدود است.

$$\bar{u}$$ و $$\tilde{u}$$ به ترتیب اجزای فرکانس‌ پایین و فرکانس‌ بالای ورودی هستند." width="508" height="111">

برای اهداف کنترل، یک مدل تحلیلی مبتنی بر دانش رفتار فیزیکی مدار، مورد نیاز است. با توجه به کاربرد مورد نظر، می‌توان از سطوح مختلف مدل‌سازی استفاده کرد. انتخاب مدل نیز بر اساس معیارهای زیر است:

• دقت مورد نیاز دینامیکی (حالت گذرا) یا حالت ماندگار
• متغیرهای درونی، ورودی یا خروجی که باید صریحاً در مدل ظاهر شوند.
• سطح پیچیدگی قابل‌ قبول
• دامنه تعریف

همه این الزامات هم‌راستا نیستند و اغلب متضاد هستند؛ به عنوان مثال، دقت پاسخ دستگاه با پیچیدگی مدل افزایش می‌یابد. بنابراین انتخاب باید بهینه باشد.

انواع مدل‌ها

برای ساده‌سازی می‌توان فرضیاتی را تعیین کرد که تأثیر چندانی بر دقت مدل و در نتیجه بر اعتبار پیاده‌سازی آن نداشته باشند:

• کلیدها «ایده‌آل» در نظر گرفته می‌شوند؛ بدین معنی که در حالت هدایت، به عنوان یک مقاومت با مقدار صفر (اصطلاحاً حالت وصل یا ON) و زمانی که خاموش هستند، مانند یک مقاومت با مقدار بی‌نهایت (اصطلاحاً حالت قطع یا OFF) رفتار می‌کنند. همچنین، زمان سوئیچینگ بی‌نهایت کوتاه فرض می‌شود.
• منابع، «ایده‌آل» در نظر گرفته می‌شوند. (برای مثال، در مورد منابع ولتاژ، توان اتصال کوتاه، بی‌نهایت است).
• عناصر پسیو، خطی و تغییر ناپذیر با زمان در نظر گرفته می‌شوند.

فیلم آموزش الکترونیک صنعتی و مبدل ها در فرادرس

کلیک کنید

گرچه مفهوم دو فرض نخست بسیار آسان است، اما باید به مورد سوم توجه بیشتری کرد. به‌ عنوان مثال، یک سلف غیرخطی را که مقدار آن هم به زمان و هم به جریان عبوری $$i(t)$$ از آن بستگی دارد نظر بگیرید. ولتاژ سلف با معادله زیر داده شده است:

$$\large v ( t  ) = \frac { d  } { d t } ( L ( i , t  ) \cdot i ( t ) )$$

بسط این معادله، یک توصیف پیچیده را نتیجه می‌دهد:

$$\large  v ( t  ) = \left ( \frac { \partial L ( i , t  ) } { \partial t } + \frac { \partial L ( i  , t ) } { \partial i } \cdot \frac { d i (  t ) } { d t } \right ) \cdot i ( t )  + L ( i  , t ) \cdot \frac { d i ( t ) }  { d t } \;\;\;\;\; (1) .$$

با توجه به پیچیدگی زیاد، معادله (۱) عملاً در مدل‌سازی غیرقابل استفاده است. علاوه‌ بر‌ این، وجود این پیچیدگی قابل توجیه نیست، چون معمولاً اولین جمله آن در بسیاری از کاربردها مهم نیست.

بیان این نکات پذیرش معقول فرضیات بالا را که در هر صورت تأثیر بنیادی بر روش مدل‌سازی ندارند توجیه می‌کند. بدیهی است که برای افزایش دقت مدل‌سازی می‌توان جزئیاتی به مدل ساده اولیه افزود. به‌ عنوان مثال، مدل عناصر مدار را می‌توان با در نظر گرفتن عناصر اتلافی (مقاومت داخلی یک منبع توان، مقاومت یک سیم‌پیچ و غیره) بهبود داد. شکل ۲ نشان می‌دهد که چگونه می‌توان مدل دیود را بهبود داد.

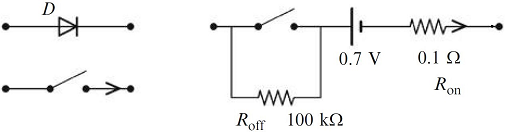
کلیدهای تک‌قطب تک‌جهته (Single-Pole–Single-Throw) یا SPST را می‌توان در مدارهای الکترونیک قدرت مختلف به کار برد. نمونه‌هایی از شماتیک این کلیدها در شکل ۳ نشان داده شده است. نماد کلیدهای تک ربعی (به‌عنوان مثال، دیود و ترانزیستور) و مشخصه‌های ایده‌آل آن‌ها در شکل ۳ (الف) و ۳ (ب) آورده شده است. کلیدهای دو‌ ربعی ولتاژ‌ دوطرفه انواع بسیاری دارند. ویژگی‌های مشترک آن‌ها - که از نظر مدل‌سازی و کنترل جذاب است - به‌ صورت یکتا یکپارچه  و در شکل ۳ (ج) نشان داده شده است.

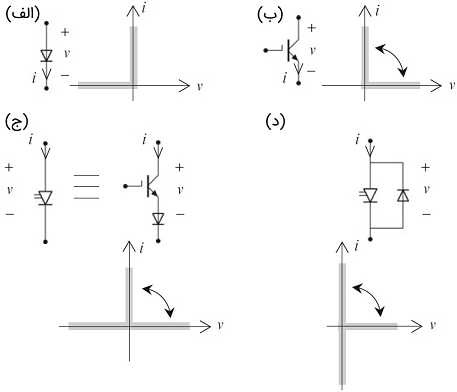
مدل سوئیچینگ

مدل سوئیچینگ مدلی کمتر کاربردی برای مبدل است؛ بدین معنی که معادلات الکتریکی را برای هر یک از پیکربندی‌های مدار توصیف می‌کند. این مدل گاهی مدل «دقیق» نیز نامیده می‌شود، زیرا با مفروضاتی که قبلاً گفته شد، رفتار مبدل را به صورت دقیق توصیف می‌کند.

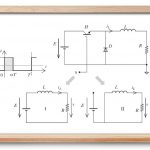
مبدل کاهنده شکل ۴ را درنظر بگیرید که در آن، کلید با سیگنال $$u(t)$$ به نام تابع سوئیچینگ تحریک می‌شود (شکل ۴ (الف)). فرض کنید $$u(t)$$ متناوب با دوره تناوب سوئیچینگ $$T$$ و نسبت وظیفه $$\alpha$$ باشد:

$$\large u ( t )  = \begin {cases} 1, & 0 \le t < \alpha T \\ 0, & \alpha T \le t < T \end {cases} , \quad u(t-T)=u(t) \, \, \, \forall t.$$

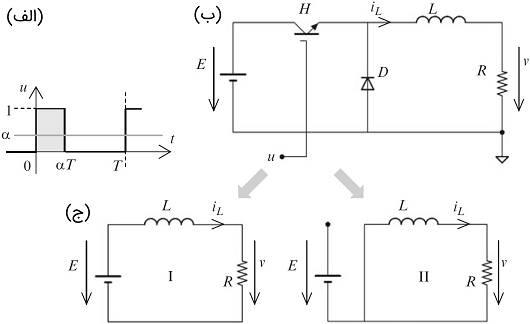$$H$$ (ب) نمودار مبدل (ج) پیکربندی‌های مختلف مبدل: پیکربندی I: بین زمان‌های $$0$$ و $$\alpha T$$ و پیکربندی II: بین زمان‌های $$\alpha T$$ و $$T$$." width="530" height="324">

به سادگی می‌توان گفت که $$\alpha$$ نشان دهنده مقدار میانگین $$u(t)$$ است.

مطابق وضعیت کلید $$H$$، مدار می‌تواند در پیکربندی I (کلید وصل) و پیکربندی II (کلید قطع) طبق شکل ۴ قرار گیرد.

پیکربندی I متناظر با زمان $$t$$ (به پیمانه $$T$$) بین $$0$$ و $$\alpha T$$ است و رفتار سیستم با معادله اول (۲) داده می‌شود. پیکربندی دوم نیز متناظر با زمان $$t$$ بین $$\alpha T$$ و $$T$$ است. مشاهده می‌شود که مدار در واقع دو عنصر سوئیچینگ دارد، چون دیود نیز به طور طبیعی قطع و وصل می‌شود. از این رو، معادلات حاکم بر آن عبارتند از:

$$\large \begin {cases} E = L \frac { d i  _ L } { d t } + R i _ L  \\ 0 =  L \frac { d i _ L  } { d t } +  R i _ L \end {cases} \;\;\;\;\; (2)$$

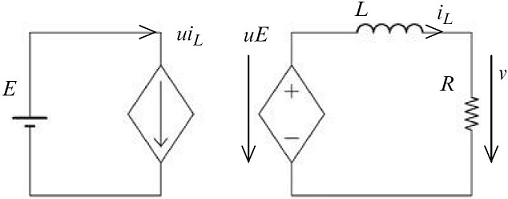
که در آن، $$v=R\cdot i_L$$. یک راه جالب برای توصیف این رفتار، استفاده از تابع سوئیچینگ $$u$$ برای فشرده‌سازی و بازنویسی (۲) به شکل زیر است:

$$\large  E \cdot u ( t ) =  L \frac { d i  _ L } { d t  } + R i _ L  . \;\;\;\;\; (3)$$

با توجه به پیکربندی، تابع $$u$$ مقادیر $$1$$ (کلید وصل) و $$0$$ (کلید صطع) را به خود می‌گیرد. این روش منجر به مدار معادل الکتریکی شکل ۵ می‌شود که آن را مدار معادل دقیق می‌نامیم.

مدل نمونه‌برداری

مدل نمونه‌برداری یا مدل داده‌های نمونه‌برداری شده (Sampled-Data Model)، مدلی است که اطلاعات حالت‌های سیستم را به شکل تناوبی ارائه می‌دهد. در این روش، نمونه‌برداری در لحظات سوئیچینگ انجام نمی‌شود، بلکه در هر دوره کامل عملکرد مبدل صورت می‌گیرد. در مورد مبدل کاهنده که در شکل ۴ نشان داده شده است، سیستم بین دو پیکربندی مداری تغییر وضعیت می‌دهد. شکل ۶ نمونه‌ای از جریان سلف را نشان می‌دهد. با توجه به مقادیر جریان در هر دوره سوئیچینگ $$T$$، معادله بازگشتی (۴) به دست می‌آید:

$$\large  i _ L (  ( K +  1 ) T ) = \left ( i _ L ( k T ) -  \frac { E } { R } \right ) \cdot e ^ { \frac { R } { L } T  } + \frac { E } { R } \cdot e ^ { -\frac { R } { L  } ( 1  - \alpha T ) } . \;\;\;\;\; (4)$$

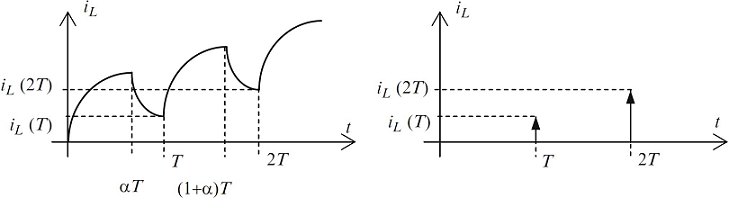
معادله (۴) را می‌توان به صورت عمومی‌تر در شکل ماتریسی (۵) نوشت:

$$\large  \mathbf { x }  _ {k +  1} = \mathbf { \Phi } ( \mathbf { x } _ k  , \mathbf { u } _  k , \mathbf { p } _ k  ) ,  \;\;\;\;\; (5)$$

که در آن، $$\mathbf{x}$$، $$\mathbf{u}$$ و $$\mathbf{p}$$ به‌ ترتیب، بردارهای حالت، ورودی کنترل و اغتشاش هستند. مدل (۵) حاوی اطلاعات حالت‌های سیستم در هر دوره نمونه‌برداری است، اما هیچ اطلاعاتی درباره متغیرها بین دو نقطه نمونه‌برداری ارائه نمی‌دهد. با توجه به توصیف زمان گسسته، می‌توان از این مدل برای کنترل دیجیتال مبدل‌ها استفاده کرد.

مدل‌های میانگین

همان‌‌گونه‌ که از نام آ­ن‌ها پیداست، این مدل‌ها رفتار میانگین حالت سیستم را نشان می‌دهند. این میانگین در مقایسه با ثابت زمانی سیستم، با یک دوره تناوب ثابت نمی‌ماند و وقتی تغییر می‌کند که سیستم تحریک شود. میانگین در یک پنجره زمانی به عرض $$T$$ محاسبه می‌شود که نسبت به دینامیک‌های سیستم به‌ اندازه کافی کوچک است. این پنجره روی محور زمان حرکت می‌کند، بنابراین میانگین لغزشی (Sliding Average) یا میانگین متحرک (Moving Average) نیز نامیده می‌شود.

برای جریان سلف مبدل، میانگین لغزشی به‌صورت رابطه (۶) بیان می‌شود:

$$\large { \langle i _ L \rangle } _  0 ( t ) = \frac {  1  } { T }  \cdot \int \limits _ { t -  T } ^ { t }   i _  L  d \tau . \;\;\;\;\; (6)$$

میانگین مدل دقیق (۳)، رابطه (۷) را نتیجه می‌دهد:

$$\large \frac { d } { d t }  { \langle i _ L\rangle } _ 0  = - \frac { R }  { L } { \langle i _ L\rangle } _ 0  + \alpha \cdot \frac { E } { L }  . \;\;\;\;\; (7)$$

رابطه (۷)، مدل میانگین مدار شکل ۴ است. جریان سلف بر حسب زمان، در شکل ۷ نشان داده شده است.

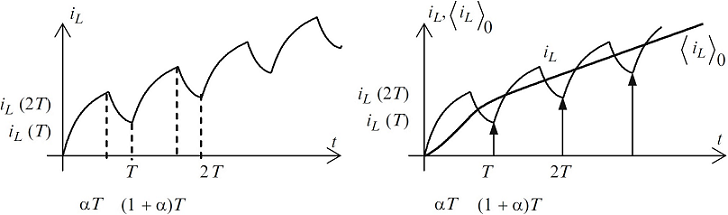
لازم به ذکر است که در زمان‌های نمونه‌برداری، مدل میانگین نسبت به مدل نمونه‌برداری دقت کمتری دارد؛ اما در عوض، حاوی اطلاعات بین زمان‌های نمونه‌برداری است.

مدل‌های سیگنال بزرگ و سیگنال کوچک

رفتار دینامیکی مبدل، جز در موارد نادر، غیرخطی است. گاهی اوقات برای تحلیل مُدال (Modal Analysis) یا طراحی قوانین کنترل خطی، باید مدل را حول یک نقطه کار معین خطی کرد. بدین منظور، از بسط سری تیلور مرتبه اول استفاده می‌شود. مدل‌های خطی شده فقط برای تغییرات اندک حول نقطه کار مورد نظر معتبر هستند. به همین دلیل، این مدل‌ها را مدل سیگنال کوچک یا مدل‌ مماسی خطی (Tangent Linear Model) می‌نامند. برخلاف مدل‌های خطی، مدل‌های اولیه که آن‌ها را مدل‌های سیگنال بزرگ می‌نامند، در کل محدوده تعریف معتبر هستند.

فیلم آموزش الکترونیک قدرت – شبیه سازی در متلب و سیمولینک در فرادرس

کلیک کنید

شکل ۸ ارتباط بین مدل سیگنال بزرگ و مدل سیگنال کوچک را برای مسیر حالت یک سیستم مرتبه‌ دوم نشان می دهد. اگر مدل سیگنال بزرگ خطی باشد، آنگاه با مدل سیگنال کوچک یکسان خواهد بود. این وضعیت به‌ ندرت رخ می‌دهد. مبدل کاهنده ایده‌آل با بار ثابت از این موارد است. این رویکرد، مشابه مدل‌سازی میانگین و نمونه‌برداری است.

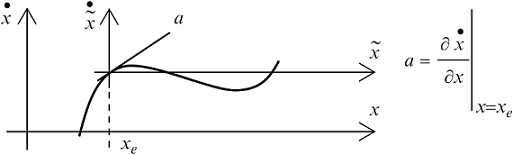
فرم کلی سیستم غیرخطی پیوسته زیر را درنظر بگیرید:

$$\large  \begin {cases} \frac { d  } { d t  } \mathbf { x }  = f ( \mathbf { x  } ( t ) ,  \mathbf { u }  ( t ) ) \\ \mathbf { y  } =  h  ( \mathbf { x }  ( t ) ,  \mathbf { u } ( t ) ) \end {cases} \;\;\;\;\; (8)$$

که در آن، $$\mathbf{x}$$، $$\mathbf{u}$$ و $$\mathbf{y}$$ به‌ ترتیب بردارهای حالت، ورودی و خروجی هستند.

محاسبه مدل حالت ماندگار

با صفر قرار دادن مشتقات می‌توان مشخصه ورودی-خروجی، یعنی مکان هندسی نقاط تعادل را در حالت ماندگار به‌ دست آورد. این نقاط با زیرنویس $$e$$ نوشته شده و با یک منحنی غیرخطی عمومی در صفحه ورودی-خروجی نمایش داده می‌شوند:

$$\large \mathbf { y }  _ e = g ( \mathbf { u  }  _ e ) .$$

تشکیل مدل سیگنال کوچک

اکنون تغییرات کوچک $$\tilde{\mathbf{x}}=\mathbf{x}-\mathbf{x}_e$$، $$\tilde{\mathbf{u}}=\mathbf{u}-\mathbf{u}_e$$ و $$\tilde{\mathbf{y}}=\mathbf{y}-\mathbf{y}_e$$ را حول نقطه تعادل $$\mathbf{y}_e$$ درنظر بگیرید که پاسخ ورودی $$\mathbf{u}_e$$ است. سیستم خطی‌ شده حول این نقطه تعادل را می‌توان به‌ شکل زیر نوشت:

$$\large \begin {cases} \dot { \tilde { \mathbf { x } } }  = \mathbf { A  } \cdot \tilde { \mathbf { x } }  + \mathbf { B  } \cdot \tilde { \mathbf { u }  } \\ \tilde { \mathbf {  y } } = \mathbf { C }  \cdot \tilde { \mathbf { x }  } + \mathbf { D }  \cdot \tilde { \mathbf { u } } \end {cases} \;\;\;\;\; (9)$$

که

$$\large \begin {cases} \mathbf { A } = \left ( \dfrac { \partial f ( \mathbf { x } , \mathbf { u }  ) } { \partial \mathbf { x  } } \right ) _ { \mathbf { x } _  e , \mathbf { u } _ e }  & \mathbf { B } = \left ( \dfrac { \partial f ( \mathbf { x } , \mathbf { u }  ) } { \partial \mathbf { u } } \right ) _ { \mathbf { x }  _ e , \mathbf { u } _ e  } \\ \mathbf { C } = \left ( \dfrac { \partial h ( \mathbf { x } , \mathbf { u } ) } { \partial \mathbf { x }  } \right ) _ { \mathbf { x } _ e , \mathbf { u }  _ e }  & \mathbf { D } = \left ( \dfrac { \partial h ( \mathbf { x } , \mathbf { u  } ) } { \partial \mathbf { u } } \right ) _ { \mathbf { x }  _ e , \mathbf { u } _ e } . \end {cases} \;\;\;\;\; (10)$$

برای سیستم‌های دو خطی، یعنی سیستم‌هایی که غیرخطی بودن آن‌ها ضرب بین دو متغیر حالت یا بین متغیر حالت و متغیر ورودی است، یک روش دیگر استفاده می‌شود که در ادامه می‌آید.

تغییرات کوچک فوق را می‌توان در مدل رابطه (۸) وارد کرده و ساده‌سازی‌های زیر را انجام داد:

• چشم‌پوشی از ضرب تغییرات متناظر با جملات مرتبه بالاتر از 2 در بسط سری‌های تیلور
• ساده‌سازی جملات متناظر با $$\mathbf{x}=0$$.

مدل حاصل، مشابه مدل خطی شده (۹) با ماتریس‌های (۱۰) است.

در اینجا یک مثال ساده را بررسی می‌کنیم. معادله (۱۱) یک سیستم دو خطی را نشان می‌دهد. از دو روش بالا برای به دست آوردن مدل سیگنال کوچک استفاده می‌کنیم.

$$\large \begin {cases} \dot { x _ 1   } = 2  x _ 1 x _ 2 - x _ 2 u \\ \dot { x _ 2 } = x_ 1 + x _ 2 \\ y = x _ 1 ^ 2 + u . \end {cases} \;\;\;\;\; (11)$$

ابتدا نقطه تعادل سیستم را برای ورودی $$u=u_e$$ به دست می‌آوریم. این کار با صفر قرار دادن مشتق متغیرهای $$x_1$$ و $$x_2$$ انجام می‌شود. با حل سیستم جبری، دو جواب به‌ دست می‌آید. برای جواب اول، واضح است که $$x_{1e}=x_{2e}=0$$ و نتیجه می‌دهد $$y_e=u_e$$. نقطه دیگر $$x_{1e}=u_e/2$$ و $$x_{2e}=-u_e/2$$ است که در نتیجه $$y_e=3u_e/4$$. در گام دوم باید ماتریس‌های مدل خطی شده سیستم را محاسبه کنیم. برای این کار، می‌توان از دو روش استفاده کرد:

• روش اول: استفاده از روابط (۱۰) برای محاسبه ماتریس‌های C ،B ،A و D:

$$\large \begin{cases} \mathbf{A}= \begin{bmatrix} \frac{\partial f_1(x,u)}{\partial x_1} & \frac{\partial f_1(x,u)}{\partial x_2} \\ \frac{\partial f_2(x,u)}{\partial x_1} & \frac{\partial f_2(x,u)}{\partial x_2} \\ \end{bmatrix} _{x_{1e}, x_{2e}, u_e} = \begin{bmatrix} -u_e & 0 \\ 1 & 1 \end{bmatrix}, \\ \mathbf{B}= \begin{bmatrix} \frac{u_e}{2} & 0 \end{bmatrix} ^T, \mathbf{C}= \begin{bmatrix} u_e & 0 \end{bmatrix} , \mathbf{D}=1. \end{cases}$$

• روش دوم: با جایگذاری تغییرات سیگنال کوچک $$\tilde{\mathbf{x}}=\mathbf{x}-\mathbf{x}_e$$ که در آن، $$\mathbf{x}^T=\begin{bmatrix} x_1 & x_2 \end{bmatrix} ^T$$، $$\mathbf{x}_e^T= \begin{bmatrix} x_{1e} & x_{2e} \end{bmatrix} ^T$$، $$\tilde{u}=u-u_e$$ و $$\tilde{y}=y-y_e$$، در مجموعه روابط (۱۱)، داریم:

$$\large \begin {cases} \dot { \tilde { x _ 1 } } +  \dot { x } _ {1e} = 2 ( \tilde { x _ 1 } +  x _{1e} ) ( \tilde { x _ 2 } + x _ {2e} )  - ( \tilde { x _ 2 } +x _  {2e} ) ( \tilde { u }+ u  _e  ) \\ \dot { \tilde { x _ 2} }  + \dot { x } _ {2e} = ( \tilde { x _ 1 } + x _{1e} ) + ( \tilde { x _ 2} + x _ {2e}  ) \\ \tilde { y } + y _ e = ( \tilde { x _ 1 } + x _  {1e})  ^ 2 + ( \tilde { u } +  u _ e  ) . \end {cases} \;\;\;\;\; (12)$$

در حالت ماندگار، سیستم با روابط (۱۳) توصیف می‌شود:

$$\large \begin{cases} 0=2x_{1e} x_{2e}-x_{2e} u_e\\ 0=x_{1e}+x_{2e}\\ y_e=x_{1e}^2+u_e. \end{cases} \;\;\;\;\; (13)$$

با انجام ضرب‌ها و چشم‌پوشی از ضرب تغییرات $$\tilde{x}_1\cdot\tilde{x}_2$$، $$\tilde{x}_1^2$$ و $$\tilde{x_2}\cdot \tilde{u}$$ و دانستن $$\dot{x}_{1e}=\dot{x}_{2e}=0$$ و نیز با توجه به رابطه (۱۳) می‌توان نوشت:

$$\large \begin {cases} \dot { \tilde { x _ 1 } } = 2 x _ {1e} \tilde { x _ 2 } + ( 2 x _ {1e} - u _ e ) \tilde { x _ 2 } -x _ {2e}  \tilde { u } \\ \dot { \tilde { x _ 2 } }  = \tilde { x _ 1 } + \tilde { x  _ 2 } \\ \tilde { y } =  2x _ {1e}   \tilde { x _ 1 } + \tilde { u } . \end{cases} \;\;\;\;\; (14)$$

با استفاده از معادله (۱۳) می‌توان مقادیر حالت ماندگار متغیرهای حالت را به عنوان توابعی از $$u_e$$ و به صورت $$x_{1e}=u_e/2$$ و $$x_{2e}=-u_e/2$$ محاسبه کرد. با جایگذاری این مقادیر، رابطه (۱۴) به شکل زیر در می‌آید:

$$\large \begin{cases} \dot{\tilde{x_1}}=-u_e\tilde{x_1}+\frac{u_e}{2}\tilde{u}\\ \dot{\tilde{x_2}}=\tilde{x_1}+\tilde{x_2}\\ \tilde{y}=u_e \tilde{x_1}+\tilde{u}. \end{cases} \;\;\;\;\; (15)$$

که ماتریس‌های C ،B ،A و D همان‌هایی هستند که از روش اول به‌ دست آمده‌اند.

مدل سیگنال کوچک را می‌توان در حوزه فرکانس یعنی به صورت تابع تبدیل نیز نمایش داد که با استفاده از ماتریس‌های استخراج شده بالا، به شکل زیر محاسبه می‌شود:

$$\large H(s) \triangleq \frac{\tilde{Y}(s)}{\tilde{U}(s)}=\mathbf{C}(s\mathbf{I}-\mathbf{A})^{-1}\mathbf{B}+\mathbf{D}$$

که در آن $$\tilde{U}(s)$$ و $$\tilde{Y}(s)$$ به‌ ترتیب تبدیلات لاپلاس سیگنال‌های زمانی اسکالر $$\tilde{u}$$ و $$\tilde{y}$$ هستند. با اعمال تبدیل لاپلاس به معادله (۱۵) می‌توان به توصیف مشابه $$H(s)$$ دست یافت. با معرفی $$\tilde{X_1}(s)$$ و $$\tilde{X_2}(s)$$ به عنوان تبدیل لاپلاس متغیرهای حالت مدل سیگنال کوچک، داریم:

$$\large \frac{\tilde{X_1}(s)}{\tilde{U}(s)}=\frac{u_e/2}{s+u_e}, \, \, \, \frac{\tilde{X_2}(s)}{\tilde{X_1}(s)} =\frac{1}{s-1}, \, \, \, \tilde{Y}(s)=u_eX_1(s)+U(s)$$

توجه کنید که $$\tilde{x_2}$$ یک حالت مشاهده ناپذیر است، زیرا در خروجی ظاهر نشده و ناپایدار نیز هست.

مدل‌‌های رفتاری

استفاده از مدل‌های جعبه سیاه برای توصیف حالت ماندگار یا مشخصه دینامیکی ورودی-خروجی سیستم‌های انتقال جریان متناوب انعطاف پذیر (FACTS) امری متداول است. چنین مدل‌هایی، مدل رفتاری (Behavioral Model) نامیده می‌شوند.

ساده‌ترین این مدل‌ها، نوع استاتیکی آن‌ها است که یک مثال از آن برای جبران‌ساز استاتیکی راکتیو (Static VAR Compensator) یا SVC در شکل ۹ (الف) نشان داده شده است. ناحیه تنظیم را می‌توان با رابطه زیر توصیف کرد:

$$\large V=V_{ref}+X_{sII}$$

که در آن، $$I$$ جریان مبادله شده بین SVC و شبکه، $$V$$ ولتاژ نقطه کوپلینگ، $$V_{ref}$$ مقدار ولتاژ مرجع و $$X_{sI}$$ شیب مشخصه تنظیم است. ادوات FACTS بسته به ولتاژ مورد نظر با یک راکتانس یا سوسپتانس مدل می‌شوند.

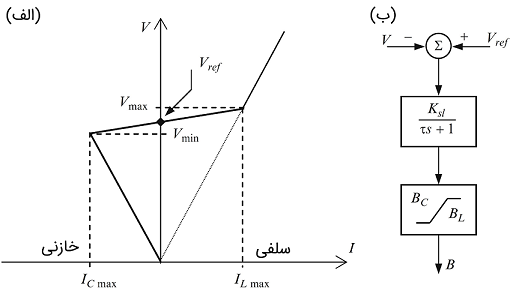
یک مدل دینامیکی ساده (مرتبه اول) را می‌توان براساس منحنی استاتیکی شکل ۹ (الف) ساخت که در شکل ۹ (ب) نشان داده شده است. جمله $$K_{sI}$$ معکوس راکتانس $$X_{sI}$$، $$\tau$$ ثابت زمانی سیستم و $$B_C$$ و $$B_L$$ به‌ ترتیب، سوسپتانس‌های متناظر با خازن و سلف SVC هستند. خروجی مدل، سوسپتانس مربوط به خطای $$V_{ref}-V$$ است.

اگر علاقه‌مند به یادگیری مباحث مشابه مطلب بالا هستید، آموزش‌هایی که در ادامه آمده‌اند نیز به شما پیشنهاد می‌شوند:

• اینورتر منبع امپدانس (Z-source Inverter) — از صفر تا صد
• آشنایی با قطعات الکترونیک قدرت — مجموعه مقالات مجله فرادرس
• مدل خط انتقال — به زبان ساده

^^