ضرب مختلط و درک مفهوم آن – به زبان ساده

در این آموزش، به توضیح ضرب مختلط و بیان عملکرد آن خواهیم پرداخت.

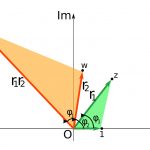
در یکی از نوشته‌های قبلی (+) بلاگ فرادرس دیدیم که اعداد موهومی در واقع به مثابه چرخشی روی محور اعداد هستند:

i که جذر 1- است، یک عدد در بُعدی کاملاً متفاوت محسوب می‌شود. زمانی که به این دریافت برسیم، می‌توانیم ضرب اعداد مختلط را به صورت ترکیب چرخش‌های دو عدد مختلط تصور کنیم:

بدین ترتیب می‌توانیم زاویه‌ها را بدون استفاده از سینوس یا کسینوس با هم جمع کنیم. شاید شما درکی شهودی از طرز عملکرد این نوع ضرب نداشته باشد؛ در این صورت در این نوشته با ما همراه باشید تا آن را به صورت کامل درک کنید.

توضیح در مورد چگونگی

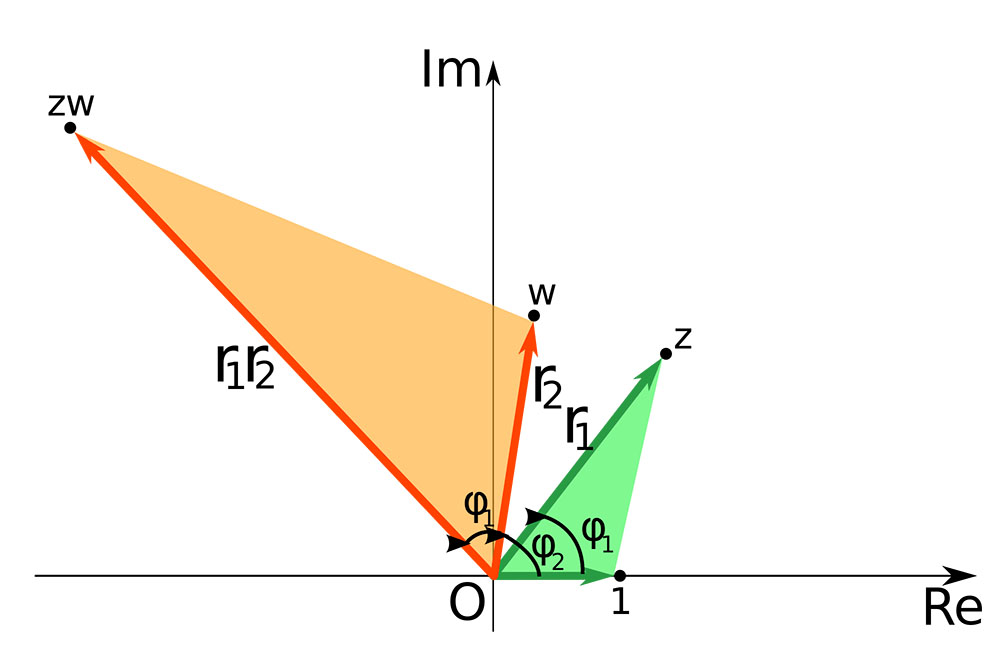
در ادامه به توضیح معمول چگونگی جمع کردن زاویه‌ها در ضرب مختلط می‌پردازیم. ابتدا اعداد مختلط را به صورت مختصات قطبی یعنی شعاع و زاویه می‌نویسیم:

سپس حاصلضرب را که بر اساس بخش‌های حقیقی و موهومی گروه‌بندی‌شده به دست می‌آوریم:

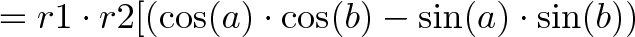
در نهایت دقت کنید که چگونه با فرمول‌های جمع زاویه سینوس و کسینوس مطابقت دارد:

می‌بینید که همین رابطه در مورد سینوس و کسینوس مجموع دو زاویه نیز برقرار است.

در واقع مشکل اینجا است که ما منطق قضیه را درک نکرده‌ایم. مثل این که بگوییم دو شعر شبیه هم هستند، چون توزیع حروفشان مانند هم است؛ با این که این توضیح صحیحی است؛ اما رضایت‌بخش نیست. در ادامه بیشتر توضیح می‌دهیم.

توضیحی ساده‌تر و جالب‌تر در مورد چرایی

باید دقت کنیم که هدف ما این است که دلیل این که وقتی دو عدد مختلط را در هم ضرب می‌کنیم، باید زوایا را با هم جمع کنیم را به درستی درک کنیم. ابتدا معنی ضرب را بررسی می‌کنیم:

• ضرب معمولی (ضرب در 2): یک عدد را به مقیاسی بزرگ یا کوچک می‌برد.
• ضرب مختلط (ضرب در i): موجب چرخش به میزان 90 درجه می‌شود.

اگر این دو تأثیر را در یک عدد مختلط ضرب کنیم چه می‌شود؟ ضرب کردن در مقدار $$(2 + i)$$ به این معنی است که عدد خود را دو برابر می‌کنیم و یک چرخش 90 درجه نیز روی آن اعمال می‌کنیم.

مثال ساده

4 × (3+i) = 4 × 3 + 4 × i = 12 + 4i

یعنی با در نظر گرفتن مقدار اولیه 4 آن را در 3 ضرب می‌کنیم و سپس تأثیر چرخش $$(+4i)$$ را نیز اضافه می‌کنیم. در این مورد نیز اگر بخواهیم تنها چرخش را داشته باشیم، باید در i ضرب کنیم. اگر بخواهیم تنها مقیاس‌بندی بکنیم باید در عدد ساده 3 ضرب کنیم. عدد مختلطی مانند (a + bi) هر دو تأثیر را می‌پذیرد.

بصری‌سازی ضرب مختلط

در مثال قبلی ضرب عدد 4 در $$(3+i)$$ را بررسی کردیم که مثال ساده‌ای محسوب می‌شود؛ اما این بار می‌خواهیم ضرب دو عدد مختلط $$(3 + 4i) × (2 + 3i)$$ را بررسی کنیم:

این مثال را می‌توان نوعی نسخه مقیاس یافته از مثلث اولیه (ضرب در 2) و افزودن مثلث مقیاس یافته/چرخش یافته (ضرب در 3i) دانست. نتیجه نهایی یک عدد مختلط جدید خواهد بود؛ اما توضیح دیگری نیز وجود دارد:

به جای گروه‌بندی ضرب بر اساس مثلث‌ها، می‌توانیم هر بخش از قاعده ضرب داخلی را جداگانه بررسی کنیم. افزودن هر جزء به معنی پیمودن یک مسیر است و ما را به نقطه مشخصی می‌رساند.

در مورد زاویه‌ها چه می‌توان گفت؟

ما در مثال قبل زاویه‌ها را با هم جمع کرده‌ایم؛ اما آیا می‌توان در این مورد مطمئن بود؟

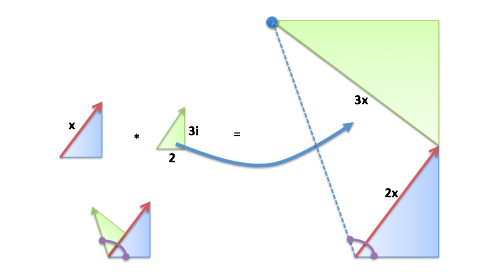
برای بررسی این پاسخ از هندسه کمک می‌گیریم. آیا خط نقطه‌چین آبی رنگ همان خطی است که از ترکیب دو مثلث به دست می‌آوریم؟

در حالت نرمال با یک مثلث $$(3 + 4i)$$ آغاز می‌کنیم و آن را روی دیگری $$(2 + 3i)$$ می‌گذاریم تا نتیجه ترکیبی را به دست آوریم.

پس از ضرب کردن کار خود را با یک مثلث مقیاس یافته (2 برابر) ادامه می‌دهیم و آن را روی مثلث مقیاس یافته دیگر (ضرب در 3) قرار می‌دهیم. با این که بزرگ‌تر است؛ اما می‌دانیم که مثلث‌های مشابه زوایای مشابهی دارند.

بنابراین ما یک مثلث را بزرگ‌تر کرده‌ایم و روی مثلث دیگر قرار داده‌ایم و چون هیچ تغییری در زاویه آن ایجاد نشده است، از این رو نتیجه یکسان است. بدین ترتیب می‌بینیم که مقیاس‌بندی مثلث و چرخش دادن آن تغییری در زوایایش ایجاد نمی‌کند. در واقع این بحث صرفاً به اعداد موهومی مربوط نمی‌شود و روشی برای ترکیب مثلث‌ها بدون استفاده از مثلثات است.

مقیاس‌بندی ممکن است تأثیرات جانبی نیز داشته باشد

دقت کنید که ساخت کپی‌های بزرگ‌تر از مثلث اولیه و افزودن آن‌ها به هم باعث تغییر در اندازه مثلث اصلی می‌شود. فرض کنید مثلث اولیه ما طولی برابر با x داشته باشد. در نهایت ما مثلثی خواهیم داشت که طول ضلع آن 2x + 3x است. از روی قضیه فیثاغورس می‌دانیم که فاصله حقیقی به صورت زیر است:

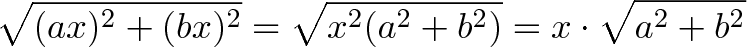
بدن ترتیب ما مثلث اولیه خود با طول ضلع x را انتخاب کرده‌ایم و آن را به اندازه مثلث جدید یعنی a+bi بزرگ کرده‌ایم. اگر مثلث جدید اندازه‌ای برابر با 1 $$(a^2 + b^2 = 1)$$ داشته باشد در این صورت فاصله تغییری نخواهد یافت.

سخن پایانی

البته اثبات‌های خشک ریاضی اشکالی ندارند؛ اما باید در مورد مفید بودن آن‌ها اندکی تأمل کنیم. اثبات‌ها دو هدف را دنبال می‌کنند:

• نشان دهند که نتیجه صحیح است. این همان هدفی است که ریاضیدان‌ها از ارائه اثبات دنبال می‌کنند. دانشجویان در کلاس ریاضی به ندرت به دنبال زیر سؤال بردن اعتبار واقعیت‌های ریاضی هستند.
• نشان دهند چرا یک نتیجه درست است.

واقعیت این است که بینش‌های عمیق از بررسی قیاس‌ها و مثال‌ها حاصل می‌شوند و نه مطالعه اثبات‌های فشرده و خشک ریاضی. جرج پولیا ریاضیدان مشهور در این خصوص می‌گوید:

«زمانی که خود را قانع کردید که قضیه‌ای درست است، می‌توانید شروع به اثبات آن بکنید.»

اگر این مطلب برایتان مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های ریاضیات
• اعداد مختلط – به زبان ساده
• مجموعه آموزش‌های دروس رسمی دبیرستان و پیش دانشگاهی
• راهنمای محاسبه با اعداد مختلط — به زبان ساده
• آموزش ریشه یابی و ترسیم اعداد مختلط در متلب
• اعداد موهومی: راهنمای تصویری و شهودی — به زبان ساده

==