فرمول محیط بیضی چیست؟ — معرفی ۹ فرمول پرکاربرد

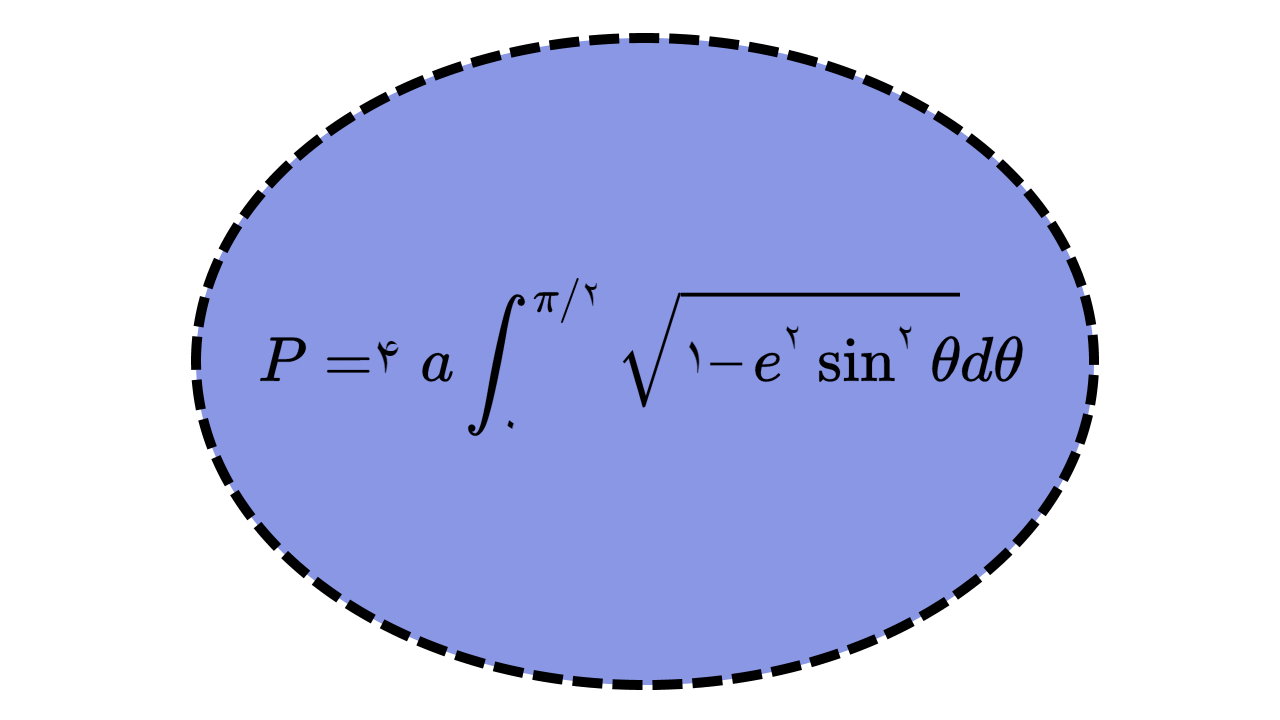
فرمول محیط بیضی، رابطه ریاضی مورد استفاده برای تعیین طول کمان این شکل هندسی است. فرمول دقیق و ثابتی برای محاسبه محیط بیضی وجود ندارد. به همین دلیل، این اندازه توسط فرمول‌ها و روابط تقریبی تعیین می‌شود. مبنای اغلب تقریب‌های محیط بیضی، فرمول محیط دایره است. در این مقاله، به معرفی ۹ فرمول محیط بیضی و ویژگی‌‌های هر یک از آن‌ها می‌پردازیم.

محیط بیضی چیست و چگونه بدست می‌آید؟

محیط بیضی، طول منحنی بسته‌ای است که مرز بیرونی این شکل هندسی را مشخص می‌کند.

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

طول این منحنی، با استفاده از اندازه شعاع‌های بزرگ و کوچک بیضی به دست می‌آید.

رابطه دقیقی برای محاسبه محیط بیضی وجود ندارد. با این حال، فرمول‌های تقریبی زیادی به منظور تعیین محیط بیضی ارائه شده‌اند که در ادامه به معرفی آن‌ها خواهیم پرداخت. پیش از این، به خاطر داشته باشید که فرمول محیط بیضی به زبان ساده برابر است با:

(میانگین شعاع بزرگ و کوچک) × عدد پی × ۲ = محیط بیضی

اغلب تقریب‌های محیط بیضی، بر اساس رابطه بالا نوشته می‌شوند. تفاوت اصلی این تقریب‌ها، نحوه محاسبه میانگین شعاع‌های بزرگ و کوچک بیضی است.

فرمول محیط بیضی چیست؟

جدول زیر، شناخته شده‌ترین و متداول‌ترین فرمول‌های محاسبه محیط بیضی را نمایش می‌دهد. در تمام این فرمول‌ها، a، شعاع بزرگ بیضی است که از تقسیم اندازه محور اصلی بر عدد ۲ به دست می‌آید. b نیز شعاع کوچک بیضی است که با تقسیم اندازه محور فرعی بر عدد ۲ محاسبه می‌شود.

از بین موارد بالا، انتگرال اول، به عنوان فرمول دقیق محیط بیضی شناخته می‌شود. با این حال، برای به دست آوردن جواب قطعی توسط این فرمول، نیاز به نوشتن بی‌نهایت عبارت وجود دارد. در اغلب ابزارهای محاسبه آنلاین محیط بیضی، تقریب دوم رامانوجان، به عنوان مبنای ریاضی اندازه‌گیری محیط مورد استفاده قرار می‌گیرد. این تقریب، اندازه محیط بیضی را با دقت مناسبی تعیین می‌کند.

فرمول اول: تقریب محیط بیضی با میانگین حسابی

دایره، حالت خاص بیضی است. از این‌رو، برخی از تقریب‌های محیط بیضی، بر اساس محیط دایره نوشته می‌شوند. فرمول محیط دایره عبارت است از:

فیلم آموزش ریاضی پایه – مرور و حل تست کنکور ارشد در فرادرس

کلیک کنید

$$C = ۲ \pi r$$

r، شعاع دایره را نمایش می‌دهد. اگر بخواهیم از این فرمول برای محاسبه محیط بیضی استفاده کنیم، باید به جای r، اندازه شعاع بیضی را قرار دهیم. چالش اصلی برای انجام این کار، متفاوت بودن اندازه شعاع‌های بیضی است.

برخلاف دایره، شعاع‌های بیضی، هم‌اندازه نیستند. بنابراین، در ساده‌ترین حالت، می‌توانیم میانگین حسابی کوچک‌ترین و بزرگ‌ترین شعاع‌های بیضی را به عنوان شعاع در رابطه بالا قرار دهیم. به این ترتیب، اولین تقریب فرمول محیط بیضی به دست می‌آید:

$$C \approx ۲ \pi (\frac { a + b }{ ۲ })$$

a و b، شعاع‌های بزرگ و کوچک بیضی هستند. عبارت داخل پرانتز نیز، میانگین حسابی این دو شعاع را نمایش می‌دهد. دقت فرمول‌های تقریبی محیط بیضی، بر اساس نسبت شعاع بزرگ به کوچک مورد بررسی قرار می‌گیرد.

به عنوان مثال، اگر نسبت a به b برابر با ۱ باشد، شکل بیضی، تفاوتی با دایره ندارد. بنابراین، جواب به دست آمده از تقریب اول، دقیق خواهد بود. با افزایش نسبت a به b، خطای این تقریب افزایش می‌یابد. در نسبت a/b=۵، میزان خطا به بیشتر از ۱۰ درصد می‌رسد. از این‌رو، کاربرد اصلی تقریب اول، در محاسبه محیط بیضی‌هایی است که اختلاف زیادی بین شعاع‌های کوچک و بزرگ آن‌ها وجود ندارد.

فرمول دوم: تقریب محیط بیضی با میانگین هندسی

دانشمند، ریاضی‌دان و ستاره‌شناس برجسته آلمانی، «یوهانس کپلر» (Johannes Kepler)، حرکت سیارات به دور خورشید را یک حرکت بیضی‌شکل معرفی کرد. او برای محاسبه مسافت طی شده توسط سیارات در حین حرکت در مدار بیضوی خود، فرمول‌های مختلفی را مورد استفاده قرار داد. یکی از این فرمول‌ها، تقریب محیط بیضی با میانگین هندسی است. این تقریب به صورت زیر نوشته می‌شود:

$$C \approx ۲ \pi \sqrt { a b }$$

فرمول بالا، به رابطه محیط دایره شباهت دارد. با این تفاوت که به جای شعاع، میانگین حسابی شعاع‌های بزرگ و کوچک بیضی مورد استفاده قرار گرفته است. خطای این فرمول در نسبت a/b>۳، به بیش از ۵۰ درصد می‌رسد. از این‌رو، مگر در نسبت‌های بسیار پایین a به b، استفاده از تقریب محیط بیضی با میانگین حسابی شعاع‌ها، گزینه مناسبی نیست.

فرمول سوم: تقریب محیط بیضی با میانگین مربعات

دو فرمول معرفی‌شده در بخش‌های قبل، مخصوصا فرمول دوم، با خطای نسبتا بالایی همراه بودند. فرمول سوم، از نظر ساختار ریاضی، به این دو فرمول شباهت دارد. با این تفاوت که به جای میانگین حسابی یا هندسی، از میانگین مربعات شعاع‌های بزرگ و کوچک در آن استفاده می‌شود. این فرمول عبارت است از:

$$C \approx ۲ \pi \sqrt { \frac { a^۲ + b^۲ } {۲} }$$

محاسبه محیط بیضی توسط فرمول بالا، دقت نسبتا خوبی را به همراه دارد. اگر نسبت a به b برابر با ۵ باشد، خطای تقریب محیط بیضی با میانگین مربعات، به نزدیکی ۸ درصد می‌رسد. با افزایش نسبت a به b و گذر آن از عدد ۱۰، مقدار خطا برابر با ۱۰ درصد می‌شود. محبوبیت این فرمول محیط بیضی به قدری زیاد است که برخی آن را به اشتباه، فرمول دقیق محیط بیضی معرفی می‌کنند.

فرمول چهارم: تقریب اول رامانوجان برای محیط بیضی

«سرینیواسا رامانوجان» (Srinivasa Ramanujan)، یکی از ریاضی‌دانان برجسته جهان، در حین مطالعات خود بر روی تقریب محیط بیضی، به رابطه‌ای دست یافت که نسبت به تقریب‌های قبلی، از دقت بسیار بالایی برخوردار است. رابطه به صورت زیر نوشته می‌شود:

$$P \approx \pi[ ۳ ( a + b ) – \sqrt{( ۳ a + b )( a + ۳ b)}]$$

خطای این فرمول در نسبت a/b=۵، چیزی حدود ۰/۰۲ درصد است. در نسبت‌های پایین‌تر a به b، خطای تقریب رامانوجان، به طور قابل‌توجهی کاهش می‌یابد. به عبارت دیگر، فرمول محیط بیضی رامانوجان، صدها یا حتی هزاران برابر بهتر از فرمول‌های قبلی عمل می‌کند.

با استفاده از نرم‌افزارهای کامپیوتری و تغییر ضرایب این فرمول، می‌توان دقت آن را تا بیش از دو برابر افزایش داد. البته، فرمول دوم رامانوجان برای محیط بیضی، نیاز به این کار را از بین می‌برد.

فرمول پنجم: تقریب دوم رامانوجان برای محیط بیضی

رامانوجان، در ادامه مطالعات خود بر روی محاسبه محیط بیضی، تقریب‌های دیگری را نیز ارائه کرد. فرمول زیر، یکی از دقیق‌ترین تقریب‌های رامانوجان برای محاسبه محیط بیضی را نمایش می‌دهد:

فیلم مجموعه آموزش ریاضیات – مقدماتی تا پیشرفته در فرادرس

کلیک کنید

$$P \approx \pi( a + b )\left( ۱ + \frac{ ۳ h }{ ۱۰ + \sqrt{ ۴ – ۳ h }}\right)$$

فرمول بالا، پیچیدگی زیادی ندارد. تنها تفاوت این فرمول با فرمول‌های قبلی، استفاده از ثابت h است. این ثابت، به صورت زیر محاسبه می‌شود:

$$h = \frac{( a – b )^{ ۲ }}{( a + b )^{ ۲ }}$$

h، یکی از پرکاربردترین ثابت‌های مورد استفاده در محاسبات مرتبط با بیضی است. مفهوم فیزیکی مشخصی برای توصیف این ثابت وجود ندارد. با این حال، به کارگیری آن در تقریب دوم رامانوجان، دقت محاسبه محیط بیضی را به میزان بسیار زیادی افزایش می‌دهد. دقت این تقریب، هزاران برابر بهتر از تقریب اول رامانوجان یا فرمول‌های برگرفته از آن است.

فرمول‌هایی که تا به اینجا معرفی کردیم، با عنوان تقریب‌های محیط بیضی شناخته می‌شوند. تمام تقریب‌ها، با مقداری خطا همراه هستند. درصد خطای هر تقریب، از مقایسه نتایج به دست آمده با مقادیر دقیق تعیین می‌شود. احتمالا با خود فکر می‌کنید که اگر امکان محاسبه دقیق محیط بیضی وجود دارد، دیگر چه نیازی به استفاده از تقریب‌ها است؟

از همه مهم‌تر، در ابتدای مقاله اشاره کردیم که هیچ فرمولی برای محاسبه مقدار واقعی محیط بیضی وجود ندارد. با توجه به این موضوع، منظور از فرمول دقیق محیط بیضی چیست؟

فرمول ششم: محاسبه دقیق محیط بیضی با سری بی نهایت

سری‌های بی‌نهایت، مجموعه‌ای از عبارت‌های نامتناهی هستند. در صورت همگرا بودن این سری‌ها، اضافه کردن هر عبارت، ما را به جواب دقیق نزدیک‌تر می‌کند. فرمول زیر، یکی از شناخته شده‌ترین و محبوب‌ترین سری‌های بی‌نهایت برای محاسبه دقیق محیط بیضی است:

$$p=\pi(a+b) \sum_{n=۰}^{\infty}\left(\begin{array}{c} ۰/۵ \\ n \end{array}\right)^{۲} h^{n}$$

در این فرمول محیط بیضی نیز مانند تقریب دوم رامانوجان، از ثابت h استفاده می‌شود. اگر سری بالا را تا n=۳ بنویسیم، به رابطه زیر می‌رسیم:

$$p=\pi ( a + b )\left(۱ + \frac{ ۱ }{ ۴ } h+\frac{ ۱ }{ ۶۴ } h^{ ۲ }+\frac{ ۱ }{ ۲۵۶ } h^{ ۳ }+\ldots\right)$$

با نوشتن سری تا n=۶، می‌توان محیط بیضی را با دقت بسیار خوبی محاسبه کرد. با این وجود، جواب قطعی محیط بیضی، فقط از حل بی‌نهایت عبارت به دست می‌آید. به همین دلیل، دستیابی به جواب قطعی، تقریبا غیر ممکن است. البته این محدودیت، تنها به محاسبه محیط بیضی اختصاص ندارد. در تمام فرمول‌ها و تقریب‌های محیط بیضی، عبارت π قابل مشاهده است.

عدد پی (π)، نسبت محیط دایره به قطر آن را نمایش می‌‌دهد. این عدد در محاسبه محیط و مساحت دایره و بیضی کاربرد دارد. در بسیاری از محاسبات مهندسی، عدد پی برابر با ۳/۱۴ در نظر گرفته می‌شود. با این وجود، محاسبه دقیق این عدد، فقط با استفاده از سری‌های بی‌نهایت یا انتگرال‌های بی‌نهایت امکان‌پذیر است.

با توجه به توضیحات بالا، امکان محاسبه محیط و مساحت بیضی و دایره به صورت قطعی وجود ندارد. با این حال، از آنجایی که عدد پی در قالب یک عبارت ثابت نظیر π ظاهر می‌شود، بسیاری از افراد، عدم وجود یک مقدار قطعی برای آن را نادیده می‌گیرند. بر اساس این نگرش، فرمول ۲πr به عنوان فرمول قطعی محیط دایره در نظر گرفته می‌شود.

برخلاف دایره، فرمول ثابتی برای محاسبه دقیق محیط بیضی تعریف نمی‌شود؛ چراکه روش یکسانی برای استفاده از اندازه شعاع‌ها وجود ندارد. در نتیجه، متغیر بودن شعاع‌های بیضی، دلیل اصلی عدم وجود یک فرمول ثابت برای محیط آن است.

فرمول هفتم: محاسبه دقیق محیط بیضی با خروج از مرکز

از دیگر فرمول‌های دقیق محاسبه محیط بیضی می‌توان به سری‌های بی‌نهایت زیر اشاره کرد:

فیلم آموزش ریاضی پایه دانشگاهی – جامع و کاربردی در فرادرس

کلیک کنید

$$p=۲ a \pi\left( ۱ -\sum_{ i = ۱ }^{\infty} \frac{( ۲ i ) !^{ ۲ }}{\left( ۲^{ i } \times i !\right)^{ ۴ }} \times \frac{e^{ ۲ i}}{ ۲ i-۱}\right)$$

اگر این سری را تا i=۳ بنویسیم، به عبارت زیر می‌رسیم:

$$p= ۲ a \pi\left[ ۱ -\left(\frac{ ۱ }{ ۲ }\right)^{ ۲ } e^{ ۲ }-\left(\frac{۱ \times ۳ }{ ۲ \times ۴ }\right)^{ ۲ } \frac{e^{ ۴ }}{ ۳ }-\left(\frac{۱ \times ۳ \times ۵ }{ ۲ \times ۴\times ۶ }\right)^{ ۲ } \frac{e^{ ۶ }}{ ۵ }-\ldots\right]$$

همان‌طور که مشاهده می‌کنید، در رابطه بالا، علاوه بر a و b به عنوان اندازه شعاع‌های بزرگ و کوچک، از ثابت e استفاده شده است. این ثابت، با عنوان «خروج از مرکز» (Eccentricity) شناخته می‌شود. خروج از مرکز، یک کمیت فیزیکی برای بیان میزان اختلاف شکل بین بیضی و دایره است. این کمیت از رابطه زیر به دست می‌آید:

$$e = \frac {\sqrt { a^۲ – b^۲ }}{ a }$$

اگر خروج از مرکز برابر با ۰ باشد، سری بی‌نهایت به شکل زیر در می‌آید:

$$p = ۲ \pi a$$

این فرمول، همان فرمول محیط دایره است. به عبارت دیگر، اگر خروج از مرکز بیضی برابر با ۰ باشد، آن یبضی یک دایره است. مقدار e بین ۰ و ۱ تغییر می‌کند. e=۱، به معنای صفر بودن b است. در این حالت، بیضی، یک خط راست با طول a در نظر گرفته می‌شود.

فرمول محیط بیضی با سری بی‌نهایت و ثابت خروج از مرکز، نتیجه قابل قبولی را به دست می‌آورد. البته در اینجا، برای دستیابی به محیط بیضی با دقتی برابر با دقت سری قبلی (فرمول ششم)، نیاز به نوشتن عبارت‌های بیشتر است.

فرمول هشتم: محاسبه دقیق محیط بیضی با انتگرال

کامل‌ترین فرمول محیط بیضی، رابطه‌ای است که بر اساس انتگرال نوشته می‌شود:

$$L = \int_{a}^{b} \sqrt{۱+\left(y^{\prime}\right)^{۲}} d x$$

بر اساس فرمول بالا، به منظور تعیین طول کمان بیضی (محیط بیضی)، به مشتق معادله آن ('y) نیاز داریم. معادله بیضی و مشتق آن عبارت هستند از:

$$\frac{x^{ ۲ }}{a^{ ۲ }}+\frac{y^{ ۲ }}{b^{ ۲ }} = ۱$$

$$y = \pm \frac{ b }{ a } \sqrt{ a^{ ۲ } – x^{ ۲ }}$$

$$y’ = \frac { -bx } { a \sqrt {a^{ ۲ } – b^{ ۲ }} }$$

با قرار دادن 'y در فرمول کامل محیط بیضی، داریم:

$$L=\int_{ a }^{ b } \sqrt{ ۱+\frac{ b^{ ۲ } x^{ ۲ }}{a^{ ۲ }\left(a^{ ۲ }-x^{ ۲ }\right)}} d x$$

اگر بازه انتگرال‌گیری را از a تا b به ۰ تا a تغییر دهیم، طول کمان بیضی در ربع اول دستگاه مختصات به دست می‌آید:

$$L=\int_{ ۰ }^{ a } \sqrt{ ۱+\frac{ b^{ ۲ } x^{ ۲ }}{a^{ ۲ }\left(a^{ ۲ }-x^{ ۲ }\right)}} d x$$

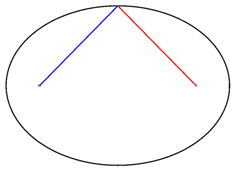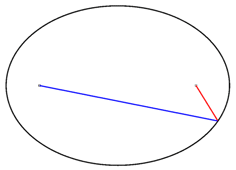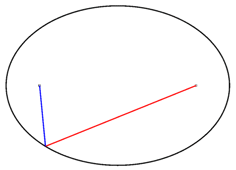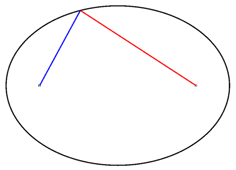
فرمول بالا، طول کمان آبی‌رنگ در تصویر زیر را محاسبه می‌کند.

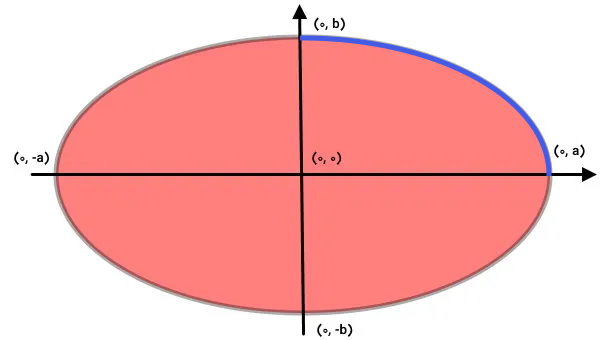
کمان نمایش داده شده در تصویر بالا، یک‌چهارم محیط بیضی است. بنابراین، به منظور تعیین محیط بیضی، باید انتگرال محاسبه طول این کمان را در عدد ۴ ضرب کنیم:

$$P = ۴ \int_{ ۰ }^{a} \sqrt{ ۱+\frac{b^{ ۲ } x^{ ۲ }}{a^{ ۲ }\left(a^{ ۲ }-x^{ ۲ }\right)}} d x$$

فرمول نهم: محاسبه دقیق محیط بیضی به صورت پارامتری

فرمول محیط بیضی با انتگرال، به صورت پارامتری نیز بیان می‌شود. اگر x و y را برابر با عبارت‌های زیر در نظر بگیریم:

$$x = a \cos { \theta }$$

$$y = b \cos { \theta }$$

فرمول پارامتری محیط بیضی به شکل زیر در می‌‌آید:

$$P = ۴ a \int_{ ۰ }^{\pi / ۲ } \sqrt{ ۱ – e^{ ۲ } \sin ^{ ۲ } \theta} d \theta$$

در این رابطه نیز مانند فرمول محیط بیضی با خروج از مرکز (فرمول هفتم)، از ثابت e استفاده می‌شود. تعیین محیط بیضی توسط فرمول بالا، با نوشتن بی‌نهایت عبارت انجام می‌گیرد.