عدد مخلوط چیست و به چه اعدادی می گویند؟ – به زبان ساده

عدد مخلوط عددی است که از ترکیب یک عدد صحیح و یک کسر ساخته می‌شود. برای مثال، $$2 \frac{1}{3}$$ عدد مخلوطی است که $$2$$ بخش عدد صحیح و $$\frac{1}{3}$$ بخش کسری در آن است. در آموزش‌های پیشین مجله فرادرس با اعداد اعشاری، کسر متعارفی و تبدیل کسر به اعشار آشنا شدیم. در این آموزش توضیح می‌دهیم عدد مخلوط چیست و چگونه تعریف می‌شود.

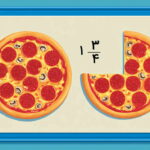
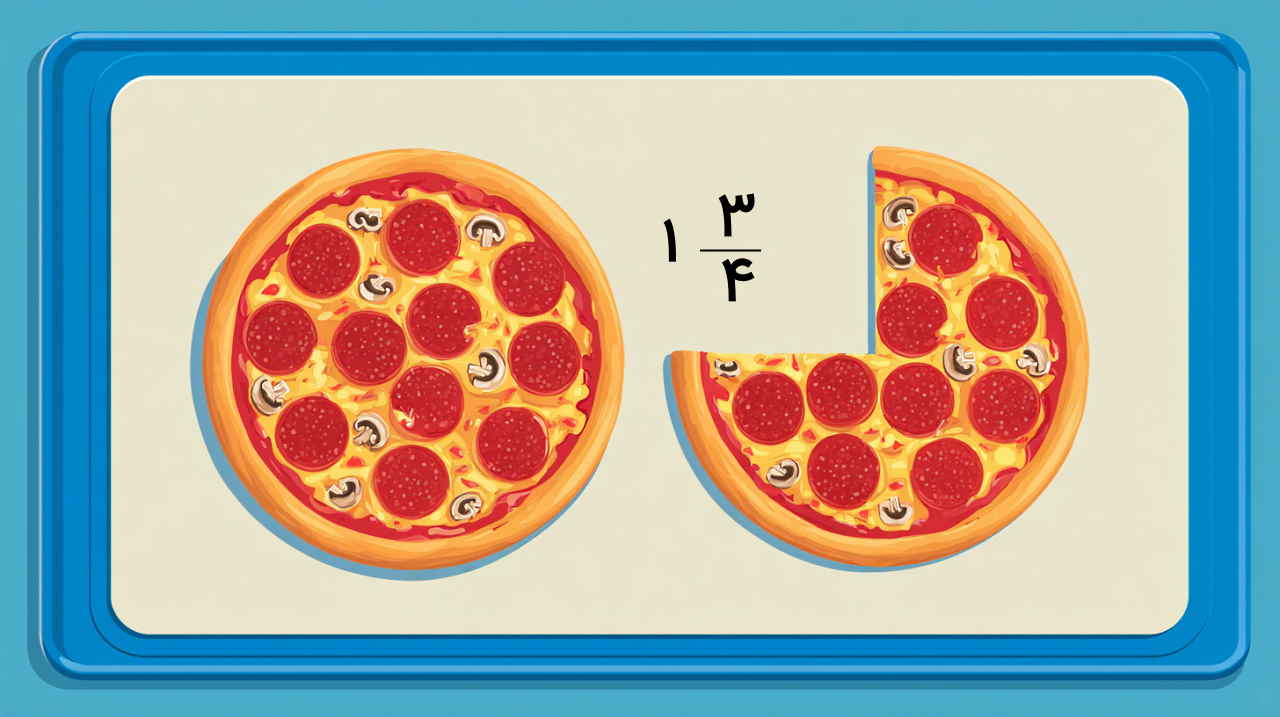
عدد مخلوط چیست؟

عدد مخلوط عددی است که از کنار هم قرار گرفتن یک عدد صحیح و یک عدد کسری ساخته می‌شود. برای نمونه اعدادی مانند $$2\frac{1}{4}$$ یا $$-5\frac{3}{7}$$ مثال‌هایی از عدد مخلوط هستند. زمانی که مقدار عدد موردنظر ما بیشتر از یک باشد و نتوانیم آن را در قالب یک بخش عددی صحیح بنویسیم، از عدد مخلوط استفاده می‌کنیم، چون عدد مخلوط به ما کمک می‌کند تا اجزای آن عدد را بهتر بفهمیم.

این عدد از عبارت انگلیسی Mixed Number به معنای عدد آمیخته گرفته شده که معادل است با ترکیب دو بخش مختلف. دقت کنید در یک عدد مخلوط همیشه قدر مطلق صورت بخش کسری از قدر مطلق مخرج آن کوچک‌تر است. تصویر زیر را در نظر بگیرید که یک کسر بزرگ‌تر از یک را نشان می‌دهد. این کسر کوچک‌تر از دو است. بنابراین می‌توانیم آن را با عدد مخلوط نمایش دهیم، زیرا یک و خرده‌ای است. این یک نشان‌دهنده عدد صحیح و خرده‌ای همان عدد کسری است.

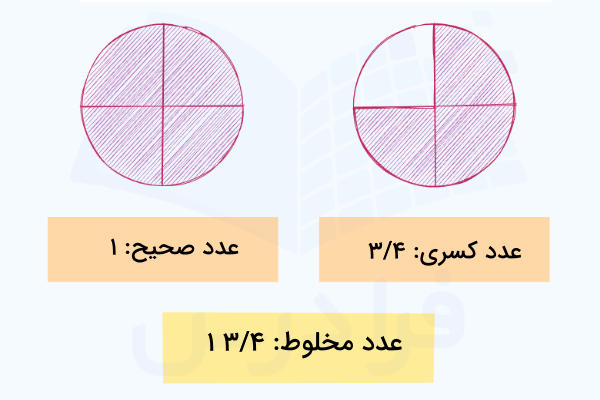
اجزای یک عدد مخلوط

همان‌طور که در بالا دیدیم، یک عدد آمیخته از دو بخش اصلی تشکیل می‌شود: یک عدد صحیح یا کامل و یک عدد کسری. به تعبیر دیگر، عدد مخلوط‌ از سه عدد دیگر تشکل می‌شود: یک عدد صحیح، یک صورت کسر و یک مخرج کسر. شکل زیر این سه عدد را نشان می‌دهد. عدد زیر را این‌گونه می‌خوانیم: دو و یک‌پنجم.

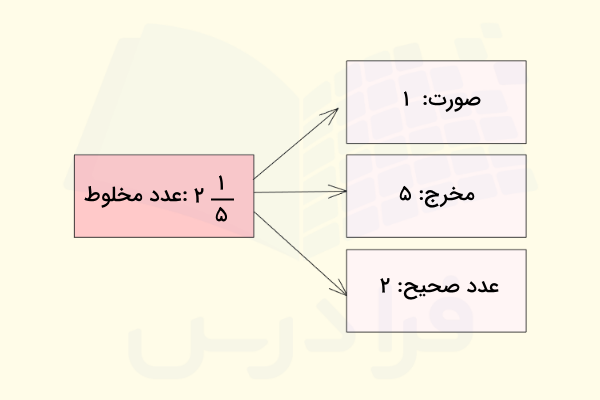
پس ویژگی‌های این نوع از اعداد را می‌توان دو مورد زیر دانست:

• بخشی از آن یک عدد صحیح است.
• بخشی از آن یک کسر است.

نمایش عدد مخلوط روی محور اعداد

همان‌طور که دیدیم، کسرهای مخلوط دو قسمت دارند، یک عدد کامل و یک کسر کوچک‌تر از واحد. برای نشان دادن اعداد مخلوط روی محور اعداد، ابتدا باید دو عدد کامل را روی محور مشخص کنیم که عدد مخلوط‌ بین آن دو قرار دارد. برای مثال، عدد مخلوط‌ $$2 \frac 35$$ بین $$2$$ و $$3$$ قرار دارد.

فیلم آموزش عدد مخلوط + معرفی، ویژگی‌های و نحوه نمایش (رایگان) در فرادرس

کلیک کنید

بنابراین، نقاط $$2$$ و $$3$$ را روی محور اعداد علامت‌گذاری می‌کنیم. مرحله بعدی این است که بخش بین $$2$$ و $$3$$ را به $$5$$ قسمت مساوی تقسیم کنیم، زیرا مخرج کسری داده شده $$5$$ است. در نهایت، باید $$3$$ خانه از $$5$$ خانه را با شروع از $$2$$ بشماریم. این نقطه همان نمایش عدد مخلوط‌ روی محور اعداد خواهد بود.

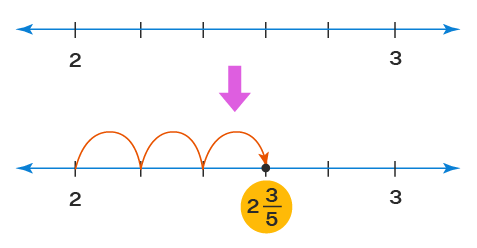
چگونه کسر را به عدد مخلوط تبدیل کنیم؟

کسر ناسره کسری است که قدر مطلق صورتش از قدر مطلق مخرجش بزرگ‌تر است. بنابراین، این کسر بزرگ‌تر از واحد است و این یعنی اینکه می‌توان آن را به‌صورت یک عدد آمیخته بیان کرد. برای تبدیل کسر به عدد مخلوط می‌توان از روش‌های مختلفی استفاده کرد که در ادامه آن‌ها را معرفی می‌کنیم.

روش اول: تقسیم صورت بر مخرج

گام‌های تبدیل کسر ناسره به عدد مخلوط‌ با این روش، به‌شرح زیر است:

1. صورت را بر مخرج کسر تقسیم کنید.
2. بعد از تقسیم، یک عدد به‌عنوان خارج قسمت خواهید داشت که همان عدد صحیح کسر مخلوط است.
3. باقیمانده تقسیم صورت کسر عدد مخلوط‌ است.
4. مخرج کسر نیز همان مخرج عدد اصلی است.

برای مثال، فرض کنید می‌خواهیم طبق گام‌های بالا، کسر $$\frac 7 3$$ را به یک عدد مخلوط‌ تبدیل کنیم. گام به گام مراحل را طی می‌کنیم:

1. عدد $$7$$ را بر $$3$$ تقسیم می‌کنیم.
2. خارج قسمت را به‌عنوان عدد صحیح می‌نویسیم.
3. باقیمانده را در صورت کسر و مقسوم‌علیه را در مخرج کسر می‌نویسیم.

شکل زیر گام‌های بالا را به‌خوبی نشان می‌دهد:

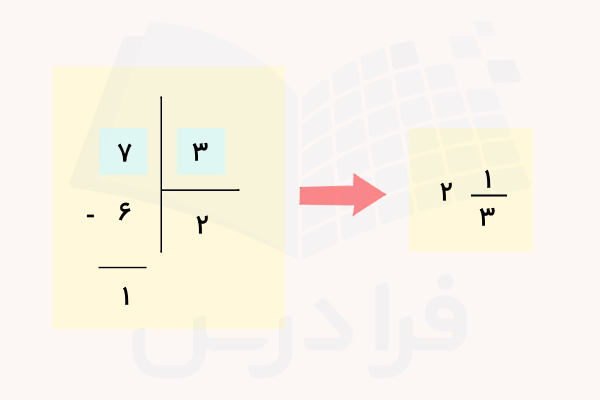
روش دوم: شکستن صورت کسر

در این روش، صورت کسر را به اندازه عدد مخرج می‌شکنیم. برای مثال، اگر عدد مخلوط $$\frac {16}{5}$$ را داشته باشیم، این‌گونه عمل می‌کنیم:

$$\large \frac {16}{5} = \frac {5+5+5+1}{5} = \frac 55 + \frac 55 +\frac 55 + \frac 15 =1+1+1+\frac 15=3\frac 15$$

روش سوم: استفاده از مضرب مخرج

در این روش، بزرگ‌ترین مضرب مخرج را که کوچک‌تر از صورت باشد، پیدا می‌کنیم و آن را با عددی جمع می‌کنیم که حاصل این جمع برابر با مخرج شود. با یک مثال، این روش را شرح می‌دهیم. فرض کنید می‌خواهیم کسر $$\frac {19}{4}$$ را به یک عدد آمیخته تبدیل کنیم. برای این کار، بزرگ‌ترین مضرب عدد $$4$$ را پیدا می‌کنیم که کوچک‌تر از $$19$$ باشد. این عدد $$16$$ است. پس می‌توانیم صورت را به‌شکل $$16+3$$‌بنویسیم. در این‌ صورت، کسر به‌شکل زیر درمی‌آید:

$$\large \frac {19}{4} = \frac {16+3}{4}=\frac {16}{4}+\frac 34= 4+\frac 34 = 4\frac 34$$

چگونه عدد مخلوط را به کسر تبدیل کنیم؟

برای تبدیل عدد مخلوط به کسر، یک مخرج مشترک می‌گیریم و عدد کامل را به‌صورت یک کسر می‌نویسیم که مخرج آن با مخرج کسر عدد مخلوط یکی است. سپس آن را با کسر عدد مخلوط جمع می‌کنیم. برای مثال، فرض کنید می‌خواهیم عدد مخلوط $$3\frac 5 7$$ را به کسر تبدیل کنیم. ابتدا می‌توانیم عدد را به‌شکل زیر بنویسیم:

$$\large 3\frac 5 7 =3+\frac57$$

فیلم چگونه کسر را ساده کنیم؟ + مثال‌های کاربردی در فرادرس

کلیک کنید

اکنون با در نظر گرفتن مخرج $$7$$، عدد $$3$$ را به یک کسر تبدیل می‌کنیم:

$$\large 3 = \frac {3\times 7}{7} = \frac {21}{7}$$

بنابراین، عدد مخلوط به‌شکل کسر زیر درمی‌آید:

$$\large 3\frac 5 7 =3+\frac57= \frac {3\times 7}{7}+\frac 57 =\frac {21}{7}+\frac 57=\frac {21+5}{7}=\frac {26}{7}$$

جمع و تفریق اعداد مخلوط

جمع اعداد مخلوط را می‌توان به سادگی و با انجام گام‌های زیر محقق کرد (مراحل را با یک مثال عددی بیان می‌کنیم). می‌خواهیم دو عدد $$5\frac 13$$ و $$7 \frac 13$$ را با هم جمع کنیم:

1.  ابتدا دو عدد مخلوط را به دو کسر ناسره تبدیل می‌کنیم که روش آن را در بخش قبل گفتیم: $$5\frac 13 = \frac {16}{3}$$ و $$7\frac13=\frac{22}{3}$$.
2. سپس دو عدد کسری را با هم جمع می‌کنیم: $$\frac {16}{3}+\frac {22}{3}=\frac {38}{3}$$
3. عدد کسری را به عدد مخلوط تبدیل می‌کنیم: $$\frac {38}{3}=\frac {36+2}{3}=\frac {36}{3}+\frac23=12+\frac 23=12\frac 23$$

برای تفریق اعداد مخلوط نیز کار مشابهی را انجام می‌دهیم.

چگونه عدد مخلوط را به عدد اعشاری تبدیل کنیم؟

برای تبدیل اعداد مخلوط به کسرها ابتدا عدد کامل را می‌نویسیم، سپس یک ممیز یا اعشار قرار می‌دهیم. سپس مخرج و صورت کسر را در عددی ضرب می‌کنیم که مخرج کسر یکی از مضرب‌های عدد $$10$$ شود. با یک مثال این فرایند را توضیح می‌دهیم.

فرض کنید می‌خواهیم عدد $$7\frac 12$$ را به یک عدد اعشاری تبدیل کنیم. ابتدا عدد $$7$$ را می‌نویسیم و در سمت راست آن یک اعشار قرار می‌دهیم. حال باید کسر $$\frac 12$$ را به‌گونه‌ای تغییر دهیم که مخرجش مضربی از $$10$$ باشد. برای این کار، صورت و مخرج را در عدد $$5$$ ضرب می‌کنیم: $$\frac 12 = \frac {1\times 5 }{2 \times 5} = \frac {5}{10}$$.

می‌بینیم که مخرج کسر مضرب $$10$$ است و به $$\frac {5}{10}$$ یا همان $$0.5$$ تبدیل شده است. بنابراین، در نهایت عدد اعشاری $$7.5$$ را خواهیم داشت. برای آشنایی بیشتر با مبحث تبدیل کسر به اعشار، به آموزش «تبدیل کسر به اعشار — به زبان ساده + حل تمرین و مثال» از مجله فرادرس مراجعه کنید.

حل مثال‌ از عدد مخلوط

در این بخش، چند مثال را از اعداد مخلوط را با هم بررسی می‌کنیم.

مثال ۱

برای شکل زیر یک عدد مخلوط و یک عدد کسری بنویسید:

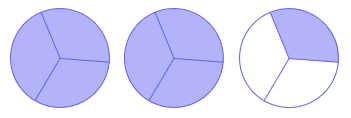
پاسخ

همان‌طور که می‌بینیم، دایره‌هایی داریم که هر کدام به سه بخش مساوی تقسیم شده‌اند. ابتدا می‌خواهیم عدد مخلوط مربوط به شکل را بنویسیم. اول اینکه سه دایره کامل داریم. این یعنی اینکه عدد کاملمان ۲ است. پس، عدد مخلوط باید به‌صورت زیر باشد:

$$\large 2\frac {\square}{\square}$$

حال باید کسر را بنویسیم. دو تا دایره کامل را کنار می‌گذاریم. یک داره ناقص داریم که یکی از سه قسمتش رنگ شده است. این یعنی اینکه یک‌سومش یا $$\frac 13$$ آن رنگ شده است. پس کل این شکل نمایانگر ۲ دایره کامل و $$\frac 13$$ یک دایره است. در نتیجه، می‌توانیم عدد مخلوط‌ را به‌صورت زیر بنویسیم:

$$\large 2 \frac 13$$

بنابراین، عدد مخلوط مربوط به این شکل دو و یک‌سوم است. اکنون باید کسر مربوط به شکل را بنویسیم. دو کار می‌توانیم انجام دهیم: یکی نوشتن از روی شکل و دیگری تبدیل عدد مخلوط‌ به یک عدد کسری. هر دو روش را بررسی می‌کنیم:

بار دیگر به شکل بالا نگاه کنید. کوچک‌ترین بخش دایره‌های یک‌سوم‌ها هستند. اینجا باید از خود بپرسیم که چند یک‌سوم رنگی داریم؟ سه تا از دایره اول، سه تا دایره دوم و یکی از دایره آخری که مجموعشان می‌شود $$7$$ تا. بنابراین، $$7$$ تا $$\frac13$$ داریم که می‌شود $$7 \times \frac 13=\frac 7 3$$. این یعنی اینکه کسر مربوط به شکل $$\frac 73$$ است. روش دوم تبدیل عدد مخلود به عدد کسری بود. این کار را به‌شکل زیر انجام می‌دهیم:

$$\large 2 \frac 13 =2+\frac 13 = \frac {2\times 3} {3} + \frac 13 = \frac {6+1}{3}=\frac 73$$

مثال ۲

عدد مخلوط مربوط به شکل زیر را بنویسید:

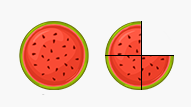
پاسخ

می‌بینیم که یک هندوانه دایره‌ای کامل داریم و یک بخش کوچک‌تر از یک. بنابراین، عدد باید بین $$1$$ و $$2$$ باشد. می‌بینیم آن تکه ناقص به $$4$$ قسمت تقسیم شده که $$3$$ بخش آن موجود است. بنابراین، عدد مخلوط $$1 \frac 34$$ است.

مثال ۳

حاصل جمع دو عدد $$\frac 14$$ و $$2\frac 13$$ را به‌دست آورید:

پاسخ

همان‌طور که می‌بینیم، یک عدد کسری و یک عدد مخلوط داریم. ابتدا عدد مخلوط را به عدد کسری تبدیل می‌کنیم:

$$\large 2\frac 13 = 2+\frac 13=\frac 63+\frac 13=\frac 73$$

بنابراین، باید دو کسر $$\frac 73$$ و $$\frac 14$$ را با هم جمع کنیم. می‌بینیم که این دو کسر مخرج‌های متفاوتی دارند. ابتدا مخرج مشترک آن‌ها را می‌گیریم و سپس آن‌ها را جمع می‌کنیم:

$$\large \frac 73 + \frac 14 = \frac {7\times 4}{12}+\frac{1\times 3}{12}=\frac {28}{12}+\frac {3}{12}= \frac {31}{12}$$

اگر بخواهیم نتیجه را به‌شکل عدد مخلوط بنویسیم، داریم:

$$\large \frac {31}{12}=\frac {24+7}{12}=\frac {24}{12}+\frac{7}{12}=2+\frac {7}{12} = 2\frac {7}{12}$$

آزمون سنجش یادگیری عدد مخلوط

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث عدد مخلوط را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.