سری زمانی با رویکرد بیزی — راهنمای کاربردی

«رگرسیون» (Regression) و تکنیک‌های آن یکی از معمول‌ترین و پرطرفدارترین روش‌های مدل‌سازی در آمار و البته در «تحلیل سری زمانی» (Time Series Analysis) است. مدل «اتورگرسیو» (Autoregressive) که با AR نشان داده می‌شود دارای یک پارامتر به نام $$p$$‌ است که براساس «تابع خودهمبستگی» (Autoregressive Function) یا ACF و «خودهمبستگی جزئی» (Partial Autoregressive Function) یا PACF تعیین می‌شود. در این نوشتار به بررسی و پیاده‌سازی مدل AR، البته با نگاهی بر «آمار بیز» (Bayesian Approach) و «قضیه بیز» (Bayesian Theorem) خواهیم پرداخت. به این ترتیب با طی کردن مراحلی، یک سری زمانی با رویکرد بیزی ایجاد خواهیم کرد. به عنوان پیش‌زمینه در این مبحث بهتر است نوشتارهای استنباط و آمار بیزی — به زبان ساده و قضیه بیز در احتمال شرطی و کاربردهای آن و همچنین تحلیل سری زمانی — تعریف و مفاهیم اولیه و سری زمانی در علم داده — از صفر تا صد را بخوانید. از طرفی مطالعه مطلب تابع خودهمبستگی (Autocorrelation Function) — مفاهیم و کاربردها نیز خالی از لطف نیست.

به منظور انجام محاسبات و پیاده‌سازی مدل AR با رویکرد بیزی در این نوشتار، از زبان برنامه‌نویسی و محاسباتی R‌ استفاده کرده‌ایم. همچنین از کتابخانه‌های ggplot ،ggplot2 ،reshape2 ،matrixStats و همچنین funplot برای انجام ترسیم‌ها و نمودارها استفاده شده است. بنابراین قبل از اجرای برنامه‌ها این بسته‌ها یا کتابخانه‌ها را روی نرم‌افزار R یا محیط Rstudio نصب کنید. برای کار در محیط برنامه‌نویسی R نیز بهتر است که از نرم‌افزار RStudio استفاده کرده تا بتوانید خروجی و روند تغییر و مقدار دهی متغیرها را به راحتی دنبال کنید. برای آشنایی بیشتر با زبان برنامه‌نویسی R و محیط نرم‌افزار Rstudio بهتر است آموزش ویدیويی فرادرس در این زمینه با عنوان آموزش برنامه نویسی R و نرم افزار RStudio و آموزش تکمیلی برنامه‌ نویسی R و نرم‌ افزار RStudio را تهیه و مشاهده کنید.

سری زمانی با رویکرد بیزی

در این نوشتار قصد داریم به کمک آمار و استنباط بیزی، رگرسیون و مدل‌سازی را برای داده‌های سری زمانی که مربوط به بانک انگلستان است، به کار بریم. این مجموعه داده‌ها، رشد شاخص GDP را در سال‌های مختلف نشان می‌دهد. در ادامه نحوه بارگذاری و استفاده از این مجموعه داده گفته خواهد شد.

فیلم آموزش تحلیل های بیزی با نرم افزار وین باگز WinBUGS در فرادرس

کلیک کنید

بهره‌گیری از آمار بیز در تجزیه و تحلیل‌های آماری، فوایدی زیادی بخصوص در سری زمانی دارد. هنگامی که در آنالیز سری زمانی، مدل‌سازی روی داده‌ها را با پارامترهای زیاد در یک مقطع یا بازه کوتاهی از زمان (مثلا در یک بازه ۳ ساله)، انجام می‌دهیم، ممکن است دچار مشکل بیش‌برازش (Overfitting) شویم. این مشکل معمولا در تحلیل داده‌های اقتصادی در مدل‌سازی روی می‌دهد. به این ترتیب مدل ایجاد شده روی داده‌های موجود خوب عمل کرده ولی قادر به پیش‌بینی برای داده‌های جدید نخواهد بود. یکی از روش‌های غلبه بر بیش‌برازش و حل این مشکل، استفاده از رویکرد بیزی و استفاده از «توزیع‌های پیشین» (Prior Distribution) برای پارامترهای مدل است.

برای آنکه بفهمیم چگونه می‌توان بر مشکل بیش‌برازش غلبه کرد به یک تکنیک رگرسیونی اشاره می‌کنیم. «رگرسیون ستیغی» (Ridge Regression) را به عنوان مثال در نظر بگیرید. در این روش رگرسیونی از یک تابع جریمه در فضای $$L2$$ استفاده می‌شود که مدل را به ازاء استفاده از پارامترهای با مقدارهای بزرگ، بیشتر جریمه می‌کند. در همین راستا اگر برای هر یک از پارامترهای مدل رگرسیونی، توزیع پیشین نرمال را انتخاب کنیم، می‌توانیم مدل رگرسیونی را براساس مشاهدات و توزیع پیشین بهینه کرده و مناسب‌ترین پارامترها را انتخاب کنیم. از طرفی استفاده از آمار بیز این اجازه را می‌دهد که به پارامترهای مدل رگرسیونی به دید متغیرهای تصادفی نگاه کرده و بنابراین انتخاب حدود و توزیع احتمالی آن‌ها در برآورد مقدارهایشان در مدل آینده موثر خواهد بود.

قضیه بیز و کاربرد آن در پیش‌بینی رگرسیونی

در دیگر نوشتارهای فرادرس با مفهوم رگرسیون چندگانه (Multiple Regression) آشنا شده‌اید. اینجا می‌خواهیم از چنین مدلی برای پیش‌بینی سری زمانی استفاده کنیم. فرض کنید مقدار مشاهده شده بردار تصادفی $$X$$ در زمان $$t$$ به صورت $$X_t$$ و متناظر با آن مقدار متغیر تصادفی $$Y$$ در زمان $$t$$ نیز به صورت $$Y_t$$‌ نشان داده شده باشد. در این صورت مدل رگرسیون خطی چند گانه به صورت زیر نوشته می‌شود.

$$\large Y_t=BX_t+\epsilon_t$$

مدل رگرسیونی

واضح است که منظور از $$\epsilon_t$$ مقدار خطای تصادفی با توزیع نرمال با میانگین صفر و واریانس $$\sigma^2$$ است.

$$\large \epsilon_t \sim N(0,\sigma^2)$$

به منظور برآورد پارامترها ($$B, \sigma^2$$) از نمونه‌های تصادفی برای هر یک از متغیرها استفاده و «تابع درستنمایی» (Likelihood Function) را مشخص می‌کنیم. در اینجا فرض بر این است که توزیع $$Y_t$$ به شرط پارامترهای $$B, \sigma^2$$ یا در حقیقت به شرط $$X_t$$، نرمال است.

$$\large f(Y_t|B,\sigma^2)=(2\pi\sigma^2)^{\frac{-n}{2}}\exp\left(-\dfrac{(Y_t-BX_t)^T(Y_t-BX_t)}{2\sigma^2} \right)$$

با استفاده از روش‌های برآورد به کمک «حداکثرسازی تابع درستنمایی» (Maximization Likelihood Function) که به واسطه لگاریتم‌گیری و محاسبه مشتق تابع درستنمایی عمل می‌کند، برآورد حداکثر درستنمایی که همان برآورد «حداقل مربعات معمولی» (OLS) است را محاسبه می‌کنیم. در این حالت برآورد پارامترهای مدل (بردار پارامترها) به صورت زیر خواهد بود.

$$\large \widehat{B}=(X_t^TX_t)^{-1}(X_t^TY_t)$$

به نظر می‌رسد که این رابطه به صورت کسری است که صورت آن کوواریانس بین $$X$$ و $$Y$$ بوده و مخرج نیز واریانس $$X$$ است. از طرفی برآورد واریانس جمله خطا نیز به صورت زیر خواهد بود.

$$\sigma^2 =\dfrac{\epsilon^T\epsilon}{n}$$

نکته: در اینجا $$n$$ تعداد مشاهدات (دنباله یا سری زمانی) و $$^T$$ نیز همان «ترانهاد» (Transpose) ماتریس یا بردار است.

تفاوت اصلی در بین روش و دیدگاه «فراوانی‌گراها» (Frequentist) و «روش‌ بیزی» (Bayesian Approach) این است که پارامترهای مدل در دیدگاه بیزی به عنوان یک متغیر تصادفی دیده می‌شوند و می‌توان به کمک داده‌ها و توزیع پیشین آن‌ها، توزیع پسین و برآوردهای مناسب‌تری را مشخص و تعیین کرد. جالب آن است که اگر هیچ اطلاعی از توزیع پیشین وجود نداشته باشد و از «توزیع جفریز» (Jeffreys Prior) استفاده شود، برآوردهای حاصل شده توسط روش بیزی با برآوردگرهای تولید شده توسط دیدگاه فراونی‌گراها یکسان خواهد بود. در جدول زیر تفاوت بین رویکرد فراوانی‌گراها و روش بیزی مشخص شده است.

به این ترتیب از «توزیع پیشین» (Prior Distribution) به عنوان اطلاعات پیشین استفاده کرده و با استفاده از قضیه بیز تابع درستنمایی را به روزآوری می‌کنیم. بهتر است ابتدا نگاهی به قضیه یا قانون بیز داشته باشیم.

قضیه بیز برای دو پیشامد $$A$$ و $$B$$ و براساس احتمال شرطی‌ آن‌ها، به صورت زیر نوشته می‌شود.

$$\large P(A|B)=\dfrac{P(B|A)P(A)}{P(B)}$$

این قضیه نشان می‌دهد، چگونه اطلاعات و دانش پیشین که براساس شواهد بدست آورده‌ایم امکان به روز رسانی تابع احتمال پسین را فراهم می‌کند. حال از این قضیه برای برآورد پارامترهای مدل رگرسیونی براساس تابع درستنمایی کمک می‌گیریم. در چنین وضعیت می‌توانیم تابع توزیع پسین را برای پارامترهای مدل به صورت زیر بنویسیم.

$$\large H(B,\sigma^2|Y_t)=\dfrac{f(Y_t|B,\sigma^2)\times f(B, \sigma^2)}{f(Y_t)}$$

رابطه ۱

حتی می‌توان، رابطه تابع احتمال پسین را به صورت ساده‌تر نیز نوشت. این کار در رابطه زیر صورت گرفته است.

$$\large H(B,\sigma^2|Y_t) \propto f(Y_t|B,\sigma^2)\times f(B, \sigma^2)$$

رابطه ۲

این رابطه از این لحاظ معنی دارد که مخرج کسر رابطه ۱ بستگی به پارامترها ندارد، پس می‌توانیم در محاسبات به منظور حداکثرسازی تابع درستنمایی آن را کنار گذشته و از آن صرف نظر کنیم. رابطه ۲ نشان می‌دهد که توزیع پسین برای پارامترها به شرط داده‌ها، متناسب با حاصلضرب تابع درستنمایی است (که ما آن را نرمال فرض کردیم) در تابع احتمال پیشین پارامترها است (که باز هم آن را هم نرمال در نظر گرفته‌ایم). برای محاسبه تابع توزیع پیشین احتیاج به «توزیع‌های حاشیه‌ای» (Marginal Distribution) و «توزیع توام» (Joint Distribution) داریم که متاسفانه مشخص کردن آن‌ها به راحتی امکان‌پذیر نیست. به این منظور از یک روش عددی به نام «نمونه‌گیری گیبز» (Gibbs Sampling) استفاده خواهیم کرد. این روش نوع خاصی از «زنجیره مارکف مونت‌کارلو» (Monte Carlo Markov Chain- MCMC) است که اجازه می‌دهد نمونه‌هایی از توزیع‌های چند متغیره به کمک توزیع شرطی ایجاد کرده و توزیع‌ توام را برآورد کنیم. در ادامه مروری بر نمونه‌گیری گیبز خواهیم داشت.

نمونه‌گیری گیبز

تصور کنید که توزیع توام برای $$n$$ متغیر تصادفی به صورت زیر باشد.

$$\large f(x_1,x_2\cdots,x_n)$$

هدف پیدا کردن توزیع حاشیه برای هر یک از متغیرهای تصادفی این توزیع توام است. اگر فرم توزیع احتمال این متغیرها مشخص نباشد، به سختی می‌توان با انتگرال‌گیری و روش تحلیلی، توزیع‌های حاشیه‌ای را مشخص کرد. در این بین نمونه‌گیری و الگوریتم گیبز قادر به برآورد توزیع‌های حاشیه‌ای برحسب توزیع شرطی است.

فیلم آموزش مقدماتی استنباط و آمار بیزی در فرادرس

کلیک کنید

ابتدا حدس اولیه‌ای برای مقدارهای نمونه تصادفی $$n$$ تایی اختیار می‌کنیم که در اینجا آن‌ها را در گام اولیه به صورت $$x_1^0,x_2^0,\cdots,x_n^0$$ نامیده‌ایم.

در گام بعد، از توزیع متغیر اول به شرط بقیه متغیرها ($$n-1$$ متغیر دیگر) نمونه تولید می‌کنیم. در حقیقت با توجه به موجود بودن توزیع شرطی این کار امکان‌پذیر است.

$$\large f(x_1^1|x_2^0,\cdots,x_n^0)$$

همین کار را در گام بعدی برای متغیر دوم انجام داده و از نمونه تولید شده قبلی که در گام پیشین تولید شده به همراه متغیرهای سوم به بعد استفاده می‌کنیم.

$$\large f(x_۲^1|x_۱^۱,x_3^0\cdots,x_n^0)$$

تکرار این گام‌ها منجر به تولید نمونه‌های تصادفی از توزیع‌های شرطی در مرحله اول می‌‌شود. همچنین با ادامه این مراحل در گام‌های بعدی، الگوریتم نمونه‌گیری گیبز نمونه‌ها را می‌سازد. به این ترتیب با این الگوریتم می‌توانیم توزیع‌های حاشیه‌ای را بوسیله همگرایی توزیع‌های شرطی بدست آوریم. فرض کنید این مراحل را به تعداد M بار تکرار کرده‌ایم. میانگین نمونه‌های تولید شده از هر یک از توزیع‌های شرطی می‌تواند میانگین توزیع پسین را نشان دهد. در تصویر زیر این مراحل را مشاهده می‌کنیم. در اینجا یک توزیع دو متغیره از $$x_1$$ و $$x_2$$ وجود دارد که احتیاج به توزیع حاشیه‌ای هر یک داریم.

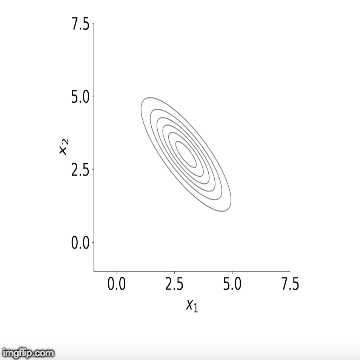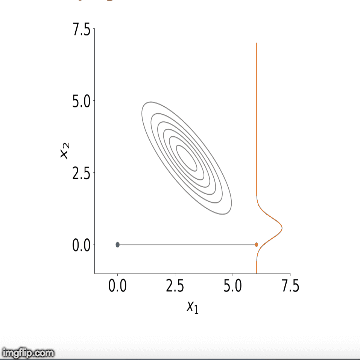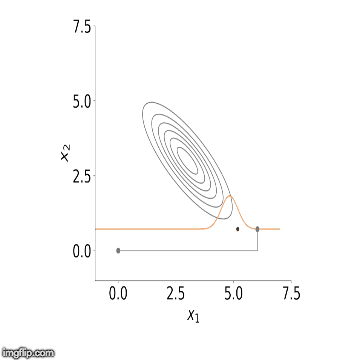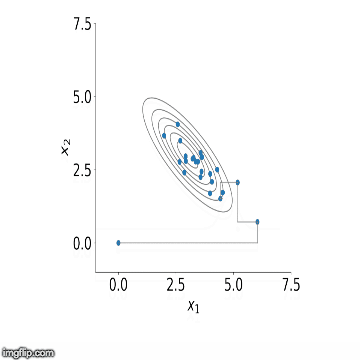
به خوبی دیده می‌شود که حتی با انتخاب نقطه‌ای خارج از تکیه‌گاه توزیع حاشیه‌ای، می‌توانیم با تکرار مراحل برآورد مناسبی از ان ایجاد کنیم. در ادامه با استفاده از نمونه‌گیری گیبز و قضیه بیز سعی خواهیم کرد با مدل (AR(2 (اتورگرسیون مرتبه ۲) مدل مناسبی برای پیش‌بینی مقادیر درصد رشد GDP ارائه کنیم و در انتها نیز به کمک یک فاصله معتبر، پارامترها را محصور کنیم.

مدل سری زمانی (AR(2

مدل سری زمانی اتورگرسیو مرتبه ۲ به صورت زیر نوشته می‌شود. این مدل بیانگر ارتباط مقدار در زمان $$t$$ با دو مقدار قبلی یعنی $$t-1$$ و $$t-2$$ است.

$$\large Y_t=a+b_1Y_{t-1}+b_2Y_{t-1}+\epsilon_t$$

مدل اتورگرسیو مرتبه ۲ - (AR(2

از طرفی می‌توان این مدل را به صورت ماتریسی نیز بیان کرد. اگر ضرایب مدل اتورگرسیو را به صورت بردار $$B$$ در نظر بگیریم، خواهیم داشت.

$$\large B=[a,b_1,b_2]$$

همچنین در ادامه ماتریس $$X$$ را به شکل زیر نمایش می‌دهیم تا بتوانیم مدل ماتریسی را ایجاد کنیم.

$$\large X_t=[1,Y_{t-1},Y_{t-2}]$$

به این ترتیب مدل اتورگرسیو را می‌توان به فرم ماتریسی مدل رگرسیونی که در بالا به آن اشاره شد، بنویسیم.

کدهای برنامه‌نویسی در R

برای انجام پیش‌بینی و برآوردهای پارامترهای سری زمانی ابتدا داده‌ها را بارگذاری می‌کنیم. این اطلاعات در قالب فایل متنی از اینجا قابل دریافت است.

1library(ggplot)
2Y.df <- read.csv('USGDP.csv', header =TRUE)
3names <- c('Date', 'GDP')
4Y <- data.frame(Y.df[,2])
5p = 2
6T1 = nrow(Y)

همانطور که دیده می‌شود مقدار تاخیر p=2‌ در مدل اتورگرسیو انتخاب شده است. البته این مدل به علت سادگی و البته کارایی انتخاب شده است. ولی می‌توانید مقدار مناسب برای p را به کمک معیارهای ارزیابی مدل مانند AIC یا BIC انتخاب کنید. نحوه محاسبه معیار AIC در زبان برنامه‌نویسی محاسباتی R در نوشتار محاسبه معیار ارزیابی AIC در R — به زبان ساده شرح داده شده است. همچنین برای استفاده از معیار BIC نیز بهتر است به مطلب معیار ارزیابی BIC در مدل های احتمالی — از صفر تا صد را نیز مطالعه کنید.

در گام بعدی به معرفی ماتریس $$X$$ و بردار ضرایب خواهیم پرداخت. برای این کار درون کد از تابع regression_matrix استفاده کرده‌ایم که دارای سه پارامتر است. این تابع، داده‌ها، مقدار تاخیر و مقدار منطقی برای مشخص کردن اینکه آیا مدل شامل مقدار ثابت ($$a$$) باشد یا خیر، را دریافت کرده و ماتریسی مانند مدل رگرسیونی برای مدل (AR(2 ایجاد می‌کند. همچنین تابع ar_companion_matrix نیز تابعی است که ماتریس ضرایب را به ماتریسی بدون مقدار ثابت تبدیل می‌کند.

1regression_matrix  <- function(data,p,constant){
2    nrow <- as.numeric(dim(data)[1])
3    nvar <- as.numeric(dim(data)[2])
4    
5    Y1 <- as.matrix(data, ncol = nvar)
6    X <- embed(Y1, p+1)
7    X <- X[,(nvar+1):ncol(X)]
8    if(constant == TRUE){
9        X <-cbind(rep(1,(nrow-p)),X)
10    }
11    Y = matrix(Y1[(p+1):nrow(Y1),])
12    nvar2 = ncol(X)
13    return = list(Y=Y,X=X,nvar2=nvar2,nrow=nrow) 
14}
15################################################################
16ar_companion_matrix <- function(beta){
17    #check if beta is a matrix
18    if (is.matrix(beta) == FALSE){
19        stop('error: beta needs to be a matrix')
20    }
21    # dont include constant
22    k = nrow(beta) - 1
23    FF <- matrix(0, nrow = k, ncol = k)
24    
25    #insert identity matrix
26    FF[2:k, 1:(k-1)] <- diag(1, nrow = k-1, ncol = k-1)
27   
28    temp <- t(beta[2:(k+1), 1:1])
29    #state space companion form
30    #Insert coeffcients along top row
31    FF[1:1,1:k] <- temp
32    return(FF)
33}

در قطعه کد بعدی به تعریف تابع regression_matrix پرداخته‌ایم و از لیست حاصل از قسمت قبل، تعداد سطرها و ماتریس‌ها را استخراج خواهیم کرد. سپس براساس تحلیل بیزی، توزیع پیشین را مشخص می‌کنیم.

1results = list()
2results <- regression_matrix(Y, p, TRUE)
3X <- results$X
4Y <- results$Y
5nrow <- results$nrow
6nvar <- results$nvar
7# Initialise Priors
8B <- c(rep(0, nvar))
9B <- as.matrix(B, nrow = 1, ncol = nvar)
10sigma0 <- diag(1,nvar)
11T0 = 1 # prior degrees of freedom
12D0 = 0.1 # prior scale (theta0)
13# initial value for variance
14sigma2 = 1

همانطور که دیده می‌شود، به عنوان توزیع پیشین برای بردار ضرایب از توزیع نرمال استفاده شده است. مشخص است که میانگین این توزیع‌ها صفر و واریانس برابر با ۱ در نظر گفته شده است. به این ترتیب بردار زیر را به عنوان بردار پارامترها مشخص کرده‌ایم.

$$\large \left(\begin{array}{c}a_0\\ b_1^0\\b_2^0\end{array}\right)=\left(\begin{array}{c}0\\ 0\\0\end{array}\right)$$

همچنین برای واریانس نیز ماتریسی به شکل زیر در نظر گرفته شده است.

$$\large \left(\begin{array}{c}\Sigma_a&0&0\\ 0&\Sigma_{b1}&0\\0&0&\Sigma_{b2}\end{array}\right)=\left(\begin{array}{c}1&0&0\\ 0&1&0\\0&0&1\end{array}\right)$$

به عنوان تابع پیشین برای پارامتر واریانس از توزیع گامای معکوس (پیشین مزدوج) استفاده شده. این توزیع اغلب به عنوان توزیع پیشین واریانس به کار می‌رود زیرا تکیه‌گاه آن اعداد مثبت است که برای بیان توزیع احتمالی واریانس مناسب است. پارامترهای توزیع گامای معکوس به صورت زیر است.

$$\large pior(\sigma^2)\sim \Gamma^{-1}(\frac{T_0}{2},\frac{\theta_0}{2})$$

در برنامه و کد نوشته شده مقدار $$T_0$=1$$

1reps = 15000
2burn = 4000
3horizon = 14
4out = matrix(0, nrow = reps, ncol = nvar + 1)
5colnames(out) <- c(‘constant’, ‘beta1’,’beta2', ‘sigma’)
6out1 <- matrix(0, nrow = reps, ncol = horizon)

در کد بالا، ماتریس‌ها و مقدارهای اولیه برای محور افقی و پیش‌بینی‌ها آماده شده‌اند. ماتریسی که به نام out ساخته‌ایم برای نگهداری نمونه‌های تصادفی تولید شده است. از آنجایی که می‌خواهیم کار مدل‌سازی را ۱۵ هزار بار تکرار کنیم، این ماتریس دارای همین تعداد سطر است. توجه داشته باشید که مدل اتورگرسیون در برنامه به صورت زیر است.

$$\large Y_t=a+b_1Y_{t-1}+b_2Y_{t-1}+\epsilon_t$$

برای پیش‌بینی مقدار در سه سال آینده احتیاج به دو مقدار پیشین داریم. به این ترتیب ماتریس دوم out1 باید ماتریسی با تعداد ستون‌هایی برابر با تعداد دوره‌های پیش‌بینی بعلاوه مقدار تاخیرها باشد که در اینجا برابر با ۱۴ خواهد بود. زیرا دوره‌های پیش‌بینی برحسب فصل است و قرار است سه سال را پیش‌بینی کنیم. در نتیجه p=3, n=4×۳=۱۲ و در نهایت تعداد ستون‌ها ماتریس out1 برابر با ۱۲+۲=۱۴ خواهد بود.

پیاده‌سازی نمونه‌گیری گیبز

در ادامه به کد مربوط به پیاده‌سازی نمونه‌گیری گیبز خواهیم رسید.

فیلم آموزش متلب با نگرش تحلیل آماری، تحلیل سری های زمانی و داده های مکانی در فرادرس

کلیک کنید

هر چند این کد ممکن است مقداری پیچیده به نظر برسد ولی با کمی تامل و دقت می‌توانید محاسبات را دنبال کنید.

1gibbs_sampler <- function(X,Y,B0,sigma0,sigma2,theta0,D0,reps,out,out1){
2for(i in 1:reps){
3    if (i %% 1000 == 0){
4    print(sprintf("Interation: %d", i))
5        }
6    M = solve(solve(sigma0) + as.numeric(1/sigma2) * t(X) %*% X) %*%
7        (solve(sigma0) %*% B0 + as.numeric(1/sigma2) * t(X) %*% Y)
8    
9    V = solve(solve(sigma0) + as.numeric(1/sigma2) * t(X) %*% X)
10    
11    chck = -1
12    while(chck < 0){   # check for stability
13        
14        B <- M + t(rnorm(p+1) %*% chol(V))
15        
16        # Check : not stationary for 3 lags
17        b = ar_companion_matrix(B)
18        ee <- max(sapply(eigen(b)$values,abs))
19        if( ee<=1){
20            chck=1
21        }
22    }
23    # compute residuals
24    resids <- Y- X%*%B
25    T2 = T0 + T1
26    D1 = D0 + t(resids) %*% resids
27    
28    # keeps samples after burn period
29    out[i,] <- t(matrix(c(t(B),sigma2)))
30    
31    
32    #draw from Inverse Gamma
33    z0 = rnorm(T1,1)
34    z0z0 = t(z0) %*% z0
35    sigma2 = D1/z0z0
36    
37    # keeps samples after burn period
38    out[i,] <- t(matrix(c(t(B),sigma2)))
39    
40    # compute 2 year forecasts
41    yhat = rep(0,horizon)
42    end = as.numeric(length(Y))
43    yhat[1:2] = Y[(end-1):end,]
44    cfactor = sqrt(sigma2)
45    X_mat = c(1,rep(0,p))
46for(m in (p+1):horizon){
47            for (lag in 1:p){
48            #create X matrix with p lags
49                X_mat[(lag+1)] = yhat[m-lag]
50    }
51            # Use X matrix to forecast yhat
52            yhat[m] = X_mat %*% B + rnorm(1) * cfactor
53    }
54    
55out1[i,] <- yhat
56}
57    return = list(out,out1)
58    }
59results1 <- gibbs_sampler(X,Y,B0,sigma0,sigma2,T0,D0,reps,out,out1)
60# burn first 4000
61coef <- results1[[1]][(burn+1):reps,]
62forecasts <- results1[[2]][(burn+1):reps,]

ابتدا، باید مقدار رشد GDP ($$Y$$) را مشخص کنیم. ماتریس $$X$$ که همان مقدارهای متغیر $$Y$$ با تاخیر زمانی ۲ است را به همراه با یک ستون از مقدارها ۱ می‌سازیم. همچنین در این مرحله به همه اطلاعات پیشین (Prior) که قبلا مشخص کرده‌ایم به همراه تعداد تکرارهای الگوریتم و دو ماتریس‌ خروجی احتیاج داریم. حلقه اصلی تکرار جایی است که باید بیشترین توجه را به آن داشته باشیم. در اینجا همه محاسبات اصلی صورت می‌گیرد. دو متغیر M و V میانگین و واریانس توزیع نرمال پسین به شرط $$B, \sigma^2$$ را تشکیل می‌دهند. به این ترتیب میانگین پارامتر $$B$$ برحسب توزیع پسین به صورت زیر محاسبه می‌شود.

$$\large M=\left( \Sigma_0^{-1}+\dfrac{1}{\sigma^2}X_t^TX_t\right)^{-1}\left( \Sigma_0)^{-1}B_0+\dfrac{1}{\sigma^2}X_t^TY_t\right)$$

همچنین واریانس پارامتر $$B$$ به شکل زیر بدست خواهد آمد.

$$\large V=\left( \Sigma_0^{-1}+\dfrac{1}{\sigma^2}X_t^TX_t\right)^{-1}$$

اگر به جمله دوم در محاسبه میانگین برآوردهای $$B$$ توجه کنید، مشخص است که می‌توانیم به جای $$Y_t$$ از برآورد درستنمایی آن استفاده کنیم. در نتیجه رابطه زیر را خواهیم داشت.

$$\large M=\left( \Sigma_0^{-1}+\dfrac{1}{\sigma^2}X_t^TX_t\right)^{-1}\left( \Sigma_0)^{-1}B_0+\dfrac{1}{\sigma^2}X_t^TX_tB_{ols}\right)$$

این عبارت بیان می‌کند که $$M$$ همان میانگین وزنی حاصل از برآورد توزیع پیشین و برآورد حداکثر درستنمایی $$B$$ است. این دقیقا نشان می‌دهد که از هر دو منبع اطلاعاتی (اطلاعات مربوط به توزیع پیشین و داده‌ها) برای برآورد پارامتر جامعه استفاده شده است. حال به واریانس توزیع پیشین توجه کنید. اگر مقدار واریانس یعنی sigma0 را کوچک انتخاب کنیم انتظار داریم که که برآورد حاصل از توزیع پسین با دقت بیشتری حاصل شود و توزیع برآوردگر، واریانس کوچکی خواهد داشت. برعکس این حالت نیز وجود دارد که با انتخاب واریانس بزرگتر برای توزیع پیشین، واریانس توزیع پسین پارامتر نیز بزرگتر و در نتیجه دقت کمتری را ارائه خواهد داد.

باز به مسئله توزیع نرمال به عنوان توزیع پیشین میانگین $$B$$ برمی‌گردیم. برای آنکه بتوانیم از یک توزیع نرمال چند متغیره با میانگین $$M$$ و ماتریس واریانس $$V$$ نمونه تولید کنیم، بهتر است مطابق رابطه زیر نمونه‌هایی مانند $$\bar{B}$$‌ از توزیع نرمال استاندارد چند متغیره تولید و آن‌ها را به نرمال چند متغیره با میانگین $$M$$ و $$V$$ تبدیل کنیم.

$$\large B^1=M+[\bar{B}\times V^{\frac{1}{2}}]^T$$

به نظر می‌رسد که فقط میانگین توزیع شرطی پسین را با حاصلضرب واریانس در مقدار تصادفی توزیع نرمال استاندارد جمع کرده‌ایم. به این ترتیب از توزیع شرطی پسین $$B$$، نمونه تولید کرده‌ایم. حال نمونه‌های تصادفی از $$B$$ را در اختیار داریم. به این ترتیب می‌توانیم نمونه تصادفی برای $$\sigma$$ را براساس «توزیع گامای معکوس» به شرط $$B$$ ایجاد کنیم. برای نمونه‌گیری از چنین توزیعی با درجه آزادی $$\frac{n}{2}$$ و پارامتر مقیاس $$\frac{\theta}{2}$$ کافی است که $$n$$ متغیر تصادفی با توزیع نرمال استاندارد به صورت $$z_0 \sim N(0,1)$$ انتخاب کنیم و تصحیح زیر را انجام دهیم.

$$\large z=\dfrac{\theta}{z^T_0z_0}$$

در این حالت $$z$$ یک نمونه از «توزیع گامای معکوس» (Inverse Gamma Distribution) خواهد بود.

کد زیر به منظور تبدیل برآوردها به یک ماتریس برای پیش‌بینی نوشته شده است. چنین ماتریس را به نام «ماتریس کلاه» (Hat Matrix) می‌شناسند. اگر دوره سری زمانی ۱۲ ساله و مقدارهای پیش‌بینی مربوط به ۳ سال آینده باشند ماتریس با اندازه 12+3 خواهیم داشت. در گام $$t+1$$ احتیاج به مقدارهای واقعی یا برآوردهای گام‌های $$t$$ و $$t-1$$‌ داریم زیرا مقدار تاخیر (Lag) را ۲ در نظر گرفته‌ایم. به این معنی که هر مقدار وابسته به دو مقدار قبل‌تر از خودش است. چنین مدلی به صورت زیر نوشته می‌شود.

$$\large \widehat{Y}_{t+1}=a+b_1\widehat{Y}_t+b_2\widehat{Y}_{t-1}+\sigma\nu^*$$

در حالت کلی ما به یک ماتریس با ابعاد $$n+p$$ احتیاج داریم که $$n$$ بیانگر تعداد دوره‌ها (مقدارهای مربوط به سری زمانی) است و $$p$$ نیز مقدار تاخیر (lag) در مدل AR را نشان می‌دهد. مدل پیش‌بینی به صورت (AR(2 در نظر گرفته و جمله خطا نیز با واریانس انتخابی $$\sigma$$ مشخص شد.

حال می‌توانیم به محاسباتی که توسط الگوریتم انجام شده نگاهی بیاندازیم. کدهایی که در زیر مشاهده می‌کنید به منظور استخراج بعضی از خصوصیات حاصل از اجرای الگوریتم روی داده‌های سری زمانی به کار رفته است. به این ترتیب میانگین‌ها برآورد حاصل برای هر یک از پارامترها محاسبه شده و نمودار فراوانی (هیستوگرام) آن‌ها ترسیم شده است.

1const <- mean(coef[,1])
2beta1 <- mean(coef[,2])
3beta2 <- mean(coef[,3])
4sigma <- mean(coef[,4])
5qplot(coef[,1], geom = "histogram", bins = 45, main = 'Distribution of Constant',
6      colour="#FF9999")
7qplot(coef[,2], geom = "histogram", bins = 45,main = 'Distribution of Beta1',
8      colour="#FF9999")
9qplot(coef[,3], geom = "histogram", bins = 45,main = 'Distribution of Beta2',
10      colour="#FF9999")
11qplot(coef[,4], geom = "histogram", bins = 45,main = 'Distribution of Sigma',
12      colour="#FF9999")

همانطور که دیده می‌شود ضرایب و پارامترهای مدل رگرسیونی AR به صورت زیر برآورد شده‌اند.

$$\large \begin{aligned}a&= 0.70\\ b_1&=1.27\\b_2&=-0.49\\ \sigma&=0.68 \end{aligned}$$

در تصویرهای زیر توزیع هر یک از پارامترهای مدل را مشاهده می‌کنید. به ترتیب در نمودار اول، توزیع مقدار ثابت $$a$$ و در نمودار دوم و سوم توزیع پارامترهای $$b_1$$ و $$b_2$$ و در نمودار چهارم نیز توزیع برآورد واریانس جمله خطا $$\sigma^2$$ نشان داده شده است.

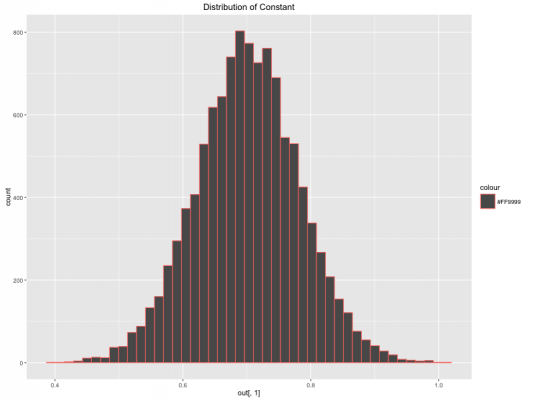
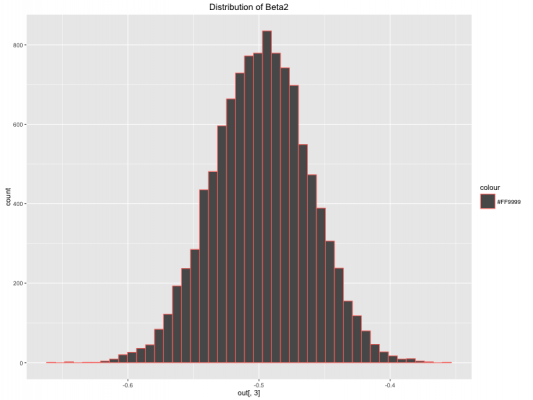
گام بعدی، استفاده از برآورد پارامتر برای رسم مقدارهای پیش‌بینی شده است. همچنین نمایش فاصله معتبر برای پیش‌بینی‌ها نیز از مواردی است که در ادامه به آن خواهیم پرداخت.

رسم نتایج حاصل از پیش‌بینی

براساس مدل بدست آمده در مراحل قبلی می‌خواهیم مقدار رشد GDP را برای سه سال آینده پیش‌بینی کنیم. توجه داشته باشید که در تحلیل بیزی قادر به نمایش حدودی برای مقدارهای پیش‌بینی هستیم که به مانند فاصله اطمینان برای مقدارهای آینده عمل می‌کند. این حدود را به نام «فاصله معتبر» (Credible Interval) می‌شناسیم. البته در اینجا منظورمان از فاصله معتبر دقیقا همان فاصله اطمینان نیست زیرا با دید فراوانی‌گراها منظور از فاصله اطمینان، حدودی است که اگر نمونه‌گیری را ۱۰۰ بار تکرار کنیم، انتظار داریم که مثلا ۹۵ فاصله شامل پارامتر باشند.

فیلم آموزش تحلیل و پیش بینی سری های زمانی در فرادرس

کلیک کنید

ولی در نگاه بیزی، پارامترهای مدل نیز متغیرهای تصادفی هستند و می‌توانیم برای آن‌ها نیز حدودی را برحسب احتمال رخداد در نظر بگیریم و بگویم که مثلا پارامتر $$B$$ با احتمال مثلا ۹۵٪ در یک فاصله یا بازه عددی قرار می‌گیرد. هر چند ممکن است این دو عبارت یک منظور را برسانند ولی با توجه به ماهیت پارامتر در هر یک از این رویکردها، شیوه بیان و تفسیر فاصله اطمینان و حدود پیش‌بینی یا فاصله معتبر، متفاوت خواهد بود.

کد زیر به منظور ترسیم حدود برای مقدارهای پیش‌بینی برای سه سال آینده نوشته شده است.

1library(matrixStats); library(ggplot2); library(reshape2)
2#uantiles for all data points, makes plotting easier
3post_means <- colMeans(coef)
4forecasts_m <- as.matrix(colMeans(forecasts))
5#Creating error bands/credible intervals around our forecasts
6error_bands <- colQuantiles(forecasts,prob = c(0.16,0.84))
7Y_temp = cbind(Y,Y)
8error_bands <- rbind(Y_temp, error_bands[3:dim(error_bands)[1],])
9all <- as.matrix(c(Y[1:(length(Y)-2)],forecasts_m))
10forecasts.mat <- cbind.data.frame(error_bands[,1],all, error_bands[,2])
11names(forecasts.mat) <- c('lower', 'mean', 'upper')
12# create date vector for plotting
13Date <- seq(as.Date('1948/07/01'), by = 'quarter', length.out = dim(forecasts.mat)[1])
14data.plot <- cbind.data.frame(Date, forecasts.mat)
15data_subset <- data.plot[214:292,]
16data_fore <- data.plot[280:292,]
17ggplot(data_subset, aes(x = Date, y = mean)) + geom_line(colour = 'blue', lwd = 1.2) + geom_ribbon(data = data_fore,
18aes(ymin = lower, ymax = upper , colour = "bands", alpha = 0.2))

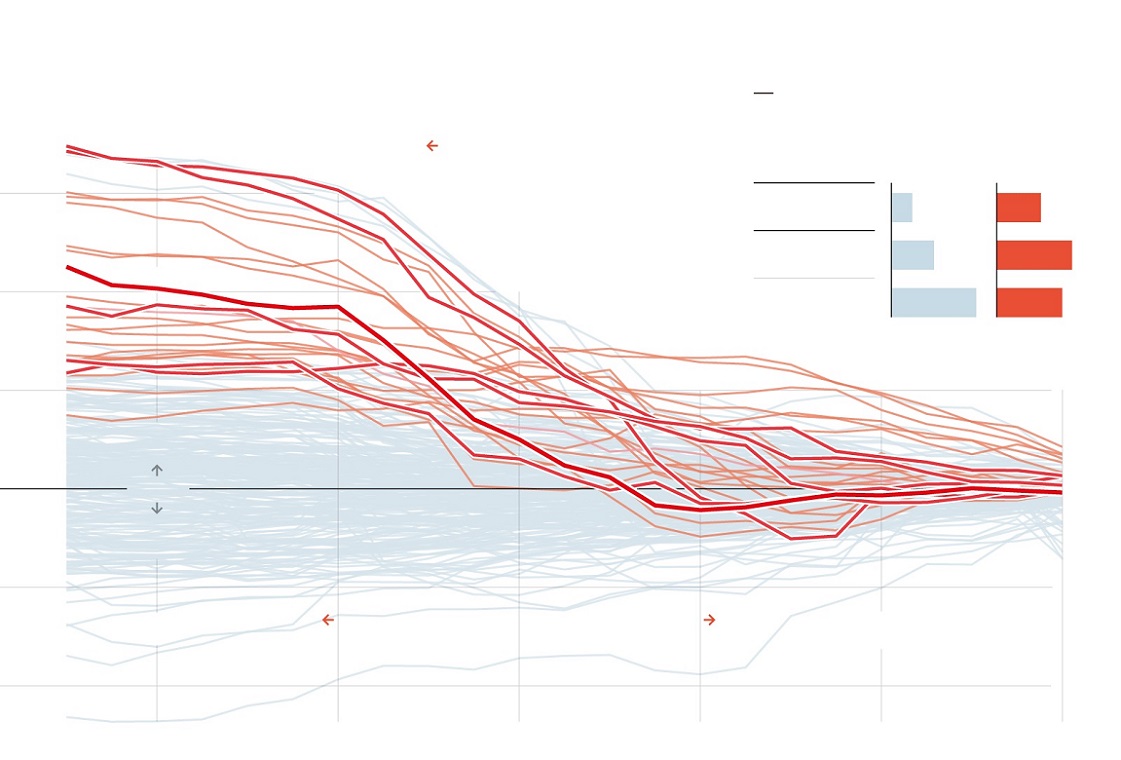
نتیجه اجرای این کد، نموداری است که در ادامه مشاهده می‌کنید. مشخص است که براساس سال‌های ۲۰۱۷ تا ۲۰۲۰ حدود پیش‌بینی ناحیه با خطوط قرمز رنگ و مقدار پیش‌بینی با رنگ آبی در میان آن‌ها دیده می‌شود. این ناحیه شامل صدک‌های ۱۶ تا ۸۴ مقدار پیش‌بینی شده هستند. هر چند این نمودار می‌تواند بیانگر حدود پیش‌بینی باشد ولی در ادامه سعی می‌کنیم که نحوه نمایش را بهبود دهیم.

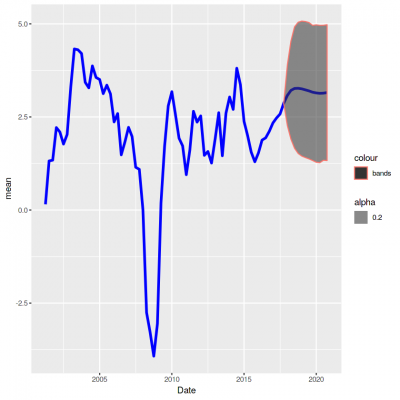
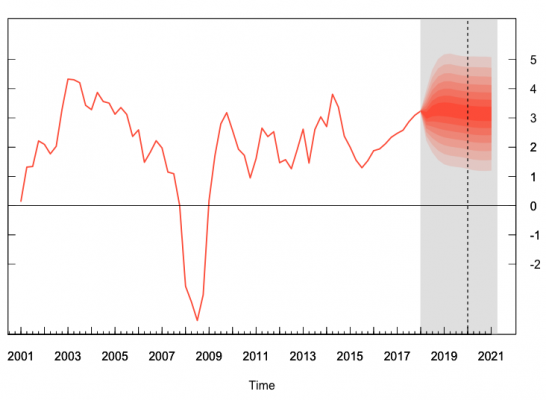
در این قسمت با استفاده از کتابخانه fanplot از بسته‌های زبان برنامه نویسی R، نموداری بهتری ترسیم کرده‌ایم که تراکم نقاط پیش‌بینی را در بازه مورد نظر به شکل مناسب‌تری نمایش می‌دهد.

1library(fanplot)
2forecasts_mean <- as.matrix(colMeans(out2))
3forecast_sd <- as.matrix(apply(out2,2,sd))
4tt <- seq(2018.25, 2021, by = .25)
5y0 <- 2018.25
6params <- cbind(tt, forecasts_mean[-c(1,2)], forecast_sd[-c(1,2)])
7p <- seq(0.10, 0.90, 0.05)
8# Calculate Percentiles
9k = nrow(params)
10gdp <- matrix(NA, nrow = length(p), ncol = k)
11for (i in 1:k) 
12    gdp[, i] <- qsplitnorm(p, mode = params[i,2], 
13                           sd = params[i,3])
14# Plot past data
15Y_ts <- ts(data_subset$mean, frequency=4, start=c(2001,1))
16plot(Y_ts, type = "l", col = "tomato", lwd = 2.5, 
17     xlim = c(y0 - 17, y0 + 3), ylim = c(-4, 6), 
18     xaxt = "n", yaxt = "n", ylab="")
19# background and fanchart
20rect(y0-0.25, par("usr")[3] - 1, y0 + 3, par("usr")[4], 
21     border = "gray90", col = "gray90")
22fan(data = gdp, data.type = "values", probs = p, 
23    start = y0, frequency = 4, 
24    anchor = Y_ts[time(Y_ts) == y0-.25], 
25    fan.col = colorRampPalette(c("tomato", "gray90")), 
26    ln = NULL, rlab = NULL)
27# BOE aesthetics
28axis(2, at = -2:5, las = 2, tcl = 0.5, labels = FALSE)
29axis(4, at = -2:5, las = 2, tcl = 0.5)
30axis(1, at = 2000:2021, tcl = 0.5)
31axis(1, at = seq(2000, 2021, 0.25), labels = FALSE, tcl = 0.2)
32abline(h = 0)
33abline(v = y0 + 1.75, lty = 2) #2 year line

همانطور که دیده می‌شود، ناحیه‌ای که با کادر خاکستری مشخص شده، ناحیه پیش‌بینی برای متغیر مستقل $$X$$ است. همچنین خطوط نارنجی که به صورت متراکم دیده می‌شوند، پیش‌بینی برای مقدار $$Y$$ را نشان می‌دهند. توجه کنید که مقدارها این متغیر روی محور عمودی و سمت راست نمایش داده شده‌اند. تراکم این نقاط در حول مرکز بیشتر و در دنباله‌ها کمتر هستند. البته همین موضوع را هم انتظار داشتیم.

خلاصه و نتیجه‌گیری

نتیجه پیش بینی ما بیانگر یک روند مثبت است. به نظر می‌رسد که متوسط رشد سالانه تا سال ۲۰۲۱ برابر با ۳٪ باشد. همچنین میزان ریسک برای رشد ۱٪ تا ۵٪ نیز تقریبا ۹۵٪ است. همچنین نمودار نشان می‌دهد که وجود رشد منفی بسیار بعید به نظر می‌رسد. که البته با توجه به سیاست‌های توسعه اقتصادی امریکا و تاثیر آن در اقتصاد جهان، صحیح به نظر می‌رسد. همانطور که دیده می‌شود، طول فاصله اطمینان ۹۵ درصدی بزرگ به نظر می‌رسد و مقدار شاخص GDP را از ۱ تا ۵ شامل می‌شود. البته برای بالا بردن دقت و کاهش طول فاصله اطمینان می‌توان از روش‌ها و تکنیک‌ها دیگر مانند Bayesian Var یا Dynamic Factor Model استفاده کرد. البته چنین مدل‌هایی دارای پیچیدگی‌های خاص خود نیز هستند و برنامه‌نویسی و پیاده‌سازی آن‌ها نیز احتیاج به زمان بیشتری دارد. به این ترتیب به نظر می‌رسد که استفاده از مدل AR بتواند توصیف مناسبی از تغییرات و پیش‌بینی سری زمانی GDP را ارائه کند.

استفاده از مدل‌های سری زمانی (حتی با در نظر گرفتن مدل ساده مثل AR) باز هم نیاز به محاسبات و زمان زیادی برای پیاده‌سازی دارد ولی این موضوعی که برایمان اهمیت دارد، پیش‌بینی نسبتا دقیقی از آینده پدیده تصادفی و فرآیند تصادفی وابسته است که توسط مدل ایجاد شده، ارائه کردیم. در این متن با استفاده از زبان محاسبات آماری R‌، توانستیم پیچیدگی‌های یک مدل سری زمانی را ساده کرده و پیش‌بینی مناسبی ارائه دهیم. با مطالعه کدهای نوشته شده می‌توانیم، مبنای محاسبات و مدل‌سازی را بهتر درک کنیم. برای ایجاد مدل از توزیع پیشین و استنباط بیزی همچنین نمونه‌گیری گبیز استفاده کردیم تا مناسب‌ترین مدل را ایجاد کنیم.

اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های پیش‌بینی و تحلیل سری‌های زمانی
• آموزش تحلیل و پیش‌بینی سری های زمانی
• مجموعه آموزش‌های آمار، احتمالات و داده‌کاوی
• آموزش متلب با نگرش تحلیل آماری، تحلیل سری های زمانی و داده های مکانی
• رگرسیون ستیغی (Ridge Regression) در پایتون — راهنمای کاربردی
• رگرسیون خطی چندگانه (Multiple Linear Regression) — به زبان ساده

^^