سرعت متوسط چیست؟ – فرمول، تعریف و محاسبه + حل تمرین

حرکت اجسام توسط عبارت‌هایی مانند تندی، سرعت، فاصله، جابجایی و شتاب، توصیف می‌شود. در بیشتر موارد، تندی و سرعت به جای یکدیگر استفاده می‌شوند، اما باید بدانیم مفاهیم آن‌ها با یکدیگر تفاوت دارد. تندی، کمیتی نرده‌ای و سرعت، کمیتی برداری است. سرعت به دو نوع سرعت متوسط و سرعت لحظه‌ای تقسیم می‌شود. همان‌طور که از نام آن‌ها مشخص است، سرعت لحظه‌ای در مورد سرعت جسم در هم لحظه از زمان و سرعت متوسط، در مورد سرعت جسم در بازه زمانی مشخصی صحبت می‌کند. در این مطلب، سرعت متوسط را توضیح می‌دهیم و تفاوت آن را با سرعت لحظه‌ای، تندی متوسط و تندی لحظه‌ای بیان می‌کنیم.

سرعت متوسط چیست ؟

فاصله خانه‌های A و B از یکدیگر برابر دو کیلومتر است. A با B تماس می‌گیرد و می‌گوید، آیا وقت داری به خانه من بیایی؟ B، با خوشحالی دعوت A را قبول می‌کند و با دوچرخه، به خانه A می‌رود. B در راه هوس بستنی می‌کند، بنابراین بدون توقف به نزدیک‌ترین بستنی‌فروشی، در فاصله ۸ کیلومتری از خانه A می‌رود. B یک ساعت پس از دوچرخه‌سواری به بستنی‌فروشی می‌رسد و پس از خرید بستنی موردعلاقه خود و A، به سمت خانه A شروع به حرکت می‌کند و یک ساعت بعد به خانه A می‌رسد. در نتیجه، B دو ساعت پس از آن‌که از خانه خود با دوچرخه راه افتاد، به خانه A می‌رسد. سوالی که مطرح می‌شود آن است که سرعت B در مسیر طی شده توسط او، چه مقدار است. دو راه برای پاسخ به این پرسش وجود دارد:

• تندی
• سرعت

تندی متوسط

به مسافت طی شده توسط جسم در واحد زمان، تندی گفته می‌شود. منظور از واحد زمان، یک ثانیه، یک دقیقه یا یک ساعت است. در این قسمت، تندی B را به‌دست می‌آوریم. ‌مسافت طی شده توسط B برابر ۱۸ کیلومتر است: دو کیلومتر فاصله خانه او تا خانه A، هشت کیلومتر فاصله خانه A تا بستنی‌فروشی و هشت کیلومتر مسیر برگشت از بستنی‌فروشی تا خانه A. مدت زمانی که ‌B این مسیر را طی کرده است در حدود دو ساعت به طول انجامید. تندی B چیست؟ برای به‌دست آوردن تندی، کافی است مسافت طی شده را بر مدت زمان لازم برای طی کردن آن مسافت، تقسیم کنیم.

$$speed = \frac{18 km}{2 h} = 9 \frac{km}{h}$$

سوالی که ممکن است مطرح شود آن است که آیا B واقعا نه کیلومتر بر ساعت حرکت کرده است. خیر، زیرا B در یک ساعت اول حرکت، دو کیلومتر و یک ساعت دوم حرکت، هشت کیلومتر رکاب زده است. مفهوم نه کیلومتر بر ساعت چیست؟ به نه کیلومتر بر ساعت، تندی متوسط گفته می‌شود. به این نکته توجه داشته باشید که B در یک ساعت اول، سریع‌تر از یک ساعت دوم حرکت، رکاب زده است. بنابراین، B با تندی یکسانی حرکت نکرده است. در اینجا، تندی را در تمام طول مسیر به‌دست آوردیم. به هنگام محاسبه تندی B، فرض می‌کنیم او مسافت‌های یکسانی را در هر ساعت،‌ طی می‌کند.

کلمه متوسط در تندی متوسط، بسیار شبیه مفهوم معدل‌گیری در دوران مدرسه است. به عنوان مثال، فرض کنید نمره شما در فیزیک برابر ۱۰ و نمره دوستتان برابر ۸ است. برای به‌دست آوردن معدل یا میانگین نمرات، آن‌ها را با یکدیگر جمع و حاصل‌ جمع را بر تعداد آن‌ها تقسیم می‌کنیم. در اینجا، میانگین نمره شما و دوستتان با هم برابر ۹ است. همان‌طور که مشاهده می‌کنید، نمره فیزیک کسی ۹ نشده است، به همین دلیل به آن میانگین یا متوسط گفته می‌شود.

نکته: برای به‌دست آوردن تندی متوسط باید مسافت کل طی شده توسط جسم را بر مدت زمان کل، تقسیم کنیم.

سرعت متوسط

به مقدار جابجایی جسم در واحد زمان، سرعت (Velocity) گفته می‌شود. هنگامی که در مورد سرعت صحبت می‌کنیم، به مسافت طی شده توسط جسم کاری نداریم، بلکه به جابجایی آن توجه می‌کنیم. بار دیگر مثال بالا را در نظر می‌گیریم. B در ابتدا کجا بود؟ در خانه خود. مکان B پس از گذشت دو ساعت کجا است؟ خانه A. شخص B در دو ساعت، چه مقدار جابجا شده است؟ دو کیلومتر، زیرا فاصله خانه B تا A برابر دو کیلومتر است. به این نکته توجه داشته باشید که در اینجا در مورد مسافت طی شده صحبت نمی‌کنیم، بلکه جابجایی شخص یا فاصله بین مکان‌های ابتدا و انتهای او برای ما مهم است. به این نکته توجه داشته باشید که به هنگام صحبت در مورد جابجایی، نه‌تنها مقدار آن، بلکه جهت جابجایی نیز باید در نظر گرفته شود. بنابراین سرعت متوسط به صورت زیر به‌دست می‌آید:

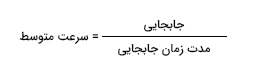
مقدار سرعت متوسط در مثال بالا برابر است با:

$$velocity = \frac{2 km}{2 h} = 1 \frac{km}{h}$$

بار دیگر به این نکته توجه داشته باشید که سرعت متوسط یک کیلومتر بر ساعت بدان معنا نیست که جسم هر یک ساعت، به اندازه یک کیلومتر جابجا می‌شود. در اینجا، سرعت متوسط در دو ساعت محاسبه شده است.

تفاوت سرعت متوسط و تندی متوسط چیست ؟

در مطالب بالا، سرعت متوسط و تندی متوسط را تعریف کردیم. در این قسمت، در مورد تفاوت این دو کمیت با جزییات بیشتری صحبت می‌کنیم. برای آن‌که تفاوت سرعت متوسط و تندی متوسط را بدانیم، باید با چند تعریف در فیزیک آشنا شویم.

• مسافت طی شده: مسافت برابر طول مسیر طی شده توسط جسم است.
• زمان سپری شده: زمان لازم برای آن‌که جسم مسافت داده شده را طی کند.
• جابجایی: جابجایی برابر کوتاه‌ترین مسافت بین نقطه آغاز و نقطه پایانی مسیر است.
• تندی: تندی برابر مسافت طی شده توسط جسم در واحد زمان و کمیتی نرده‌ای است، یعنی جهت مشخصی ندارد. تندی به ما می‌گوید جسم تا چه اندازه سریع حرکت می‌کند. به بیان دیگر، تندی، تغییرات مسافت طی شده توسط جسم، در بازه زمانی مشخصی را به ما نشان می‌دهد.
• سرعت: سرعت برابر جابجایی کل جسم در جهت مشخص در واحد زمان و کمیتی برداری است. بنابراین، علاوه بر اندازه، جهت نیز دارد. سرعت را به صورت تغییرات جابجایی نسبت به زمان نیز تعریف می‌کنیم.

تفاوت اصلی بین سرعت و تندی آن است که تندی کمیتی نرده‌ای، اما سرعت کمیتی برداری است. دلیل این موضوع آن است که مسافت طی شده توسط جسم، کمیتی برداری است و به مسیر حرکت جسم بستگی دارد. اما جابجایی کمیتی برداری و تنها به نقاط ابتدا و انتهای حرکت، وابسته است.

سرعت متوسط در حرکت بر خط راست

در مطالب بالا گفتیم، سرعت متوسط از تقسیم جابجایی بر مدت زمان جابجایی به‌دست می‌آید. بنابراین، سرعت متوسط کمیتی برداری و دارای اندازه و جهت است. اگر جسمی بر روی خط راست حرکت کند، سرعت متوسط آن را می‌توان به صورت زیر به‌دست آورد.

$$v_ { average} = \overline{v} = \frac{x_2 - x_ 1 }{t _ 2 - t _ 1} = \frac{\triangle x}{\triangle t}$$

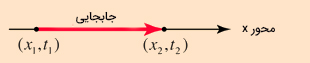
در رابطه بالا، $$x_ 1$$ مکان ذره زمان $$t_1$$ و $$x_2$$ مکان ذره در مکان $$t_2$$ است. اگر جسمی با شتاب ثابت روی خط راست حرکت کند و سرعت‌های اولیه و نهایی آن مشخص باشند، سرعت متوسط را می‌توان با استفاده از رابطه زیر نیز به‌دست آورد:

$$v_ { average} = \overline{v} = \frac{v_1 + v _ 2 }{2}$$

مثال اول

مردی روی خطی مستقیم به سمت راست حرکت می‌کند. او ابتدا مسیرِ هفت کیلومتری را در دو ساعت طی می‌کند و پس از مدت بسیار کوتاهی استراحت، دو کیلومتر دیگر در امتداد همان مسیر، به مدت یک ساعت حرکت می‌کند.

1. تندی متوسط مرد را برای تمام مسیر به‌دست آورید.
2. سرعت متوسط او را برای تمام مسیر محاسبه کنید.

پاسخ

در این مثال، حرکت روی خط مستقیم و در یک جهت انجام شده است. مسیر طی شده توسط فرد به دو قسمت تقسیم می‌شود:

1. ابتدا، مسیر هفت کیلومتری را به مدت دو ساعت طی می‌کند.
2. در ادامه، آهسته‌تر حرکت می‌کند و مسیر دو کیلومتری را به مدت یک ساعت طی می‌کند.

قسمت ۱: در این قسمت، تندی متوسط را به‌دست می‌آوریم. با توجه به مطالب گفته شده در بخش‌های قبل، تندی متوسط برابر مسافت طی شده توسط فرد تقسیم بر مدت زمان کل است. مسافت کل برابر نه کیلومتر و مدت زمان کل برابر ۳ ساعت است. بنابراین، تندی برابر است با:

$$S = \frac{9 km}{3 h} = 3 \frac{km}{h}$$

قسمت ۲: در این قسمت، سرعت متوسط را به‌دست می‌آوریم. با توجه به مطالب گفته شده در بخش‌های قبل، سرعت متوسط برابر جابجایی طی شده توسط فرد تقسیم بر مدت زمان کل است. از آنجا که مسیر حرکت فرد تغییر نکرده است و مسیر دوم در امتداد مسیر اول است، مسافت طی شده برابر جابجایی است. از این‌رو، جابجایی برابر ۹ کیلومتر است و سرعت متوسط برابر است با:

$$\overline{V} = \frac{9 km}{3 h} = 3 \frac{km}{h}$$

همان‌طور که می‌دانیم یکای استاندارد سرعت، برابر متر بر ثانیه است و در این مثال، یکای سرعت برحسب کیلومتر بر ساعت به‌دست آمده است.

پرسش: سرعت را برحسب متر بر ثانیه به‌دست آورید.

پاسخ: برای تبدیل کیلومتر بر ساعت به متر بر ثانیه باید کیلومتر را به متر و ساعت را به ثانیه تبدیل کنیم. با توجه به آن‌که هر کیلومتر برابر ۱۰۰۰ متر و هر ساعت برابر ۳۶۰۰ ثانیه است، داریم:

$$3 \frac { km} {h} = 3 \times \frac{1000 m}{3600 s} = 3 \times \frac{10}{36} = 0.83 \frac{m}{s}$$

مثال دوم

مردی برای رفتن به خانه ابتدا باید، هفت کیلومتر به سمت شرق و سپس ۲/۵ کیلومتر به سمت غرب برود. اگر مدت زمان هر مسیر به ترتیب برابر دو ساعت و یک ساعت باشد، تندی متوسط و سرعت متوسط او را در تمام مسیر به‌دست آورید.

پاسخ

در این مثال، حرکت روی خط مستقیم و در دو جهت مخالف انجام شده است. مسیر طی شده توسط فرد به دو قسمت تقسیم می‌شود:

1. ابتدا، مسیر هفت کیلومتری را به مدت دو ساعت به سمت شرق طی می‌کند.
2. در ادامه، آهسته‌تر حرکت می‌کند و مسیر ۲/۵ کیلومتری را به مدت یک ساعت، به سمت غرب طی می‌کند.

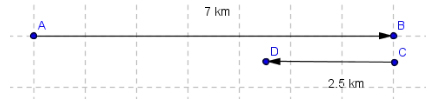
از آنجا که دو مسیر در خلاف جهت یکدیگر هستند، مسافت و جابجایی و در نتیجه، تندی و سرعت متوسط با یکدیگر برابر نیستند.

قسمت ۱: در این قسمت، تندی متوسط را به‌دست می‌آوریم. تندی متوسط برابر مسافت طی شده توسط فرد تقسیم بر مدت زمان کل است. مسافت کل برابر ۹/۵ کیلومتر و مدت زمان کل برابر ۳ ساعت است. بنابراین، تندی برابر است با:

$$S = \frac{9.5 km}{3 h} = 3.2 \frac{km}{h}$$

قسمت ۲: در این قسمت، سرعت متوسط را به‌دست می‌آوریم. سرعت متوسط برابر جابجایی طی شده توسط فرد تقسیم بر مدت زمان کل است. از آنجا که مسیر حرکت فرد تغییر کرده و مسیر دوم در خلاف جهت مسیر اول است، مسافت طی شده با جابجایی برابر نیستند و جابجایی برابر ۴/۵ کیلومتر خواهد بود:

$$\overline{V} = \frac{4.5 km}{3 h} = 1.5 \frac{km}{h}$$

مثال سوم

قطاری در امتداد خط راست با سرعت ثابت ۶۰ کیلومتر بر ساعت حرکت می‌کند. سرعت قطار پس از طی مسافت d با سرعت 60 کیلومتر بر ساعت، به ۸۰ کیلومتر بر ساعت می‌رسد و مسافت 2d را با همین سرعت طی می‌کند. سرعت متوسط قطار را به‌دست آورید.

پاسخ

در این مثال، حرکت روی خط مستقیم و در یک جهت انجام شده است. مسیر طی شده توسط قطار به دو قسمت تقسیم می‌شود:

1. ابتدا، مسیر d کیلومتری را با سرعت ثابت ۶۰ کیلومتر بر ساعت طی می‌کند.
2. در ادامه، تندتر حرکت می‌کند و مسیر d کیلومتری را با سرعت ۸۰ کیلومتر بر ساعت طی می‌کند.

برای به‌دست آوردن سرعت متوسط کل، ابتدا زمان هر قسمت از حرکت قطار را به‌دست می‌آوریم.

زمان کل برای قسمت اول حرکت: زمان $$t_1$$ برای طی کردن مسیر d با سرعت ثابت ۶۰ کیلومتر بر ساعت برابر است با:

$$t_1 = \frac{d}{60}$$

زمان کل برای قسمت دوم حرکت: زمان $$t_2$$ برای طی کردن مسیر 2d با سرعت ثابت ۸۰ کیلومتر بر ساعت برابر است با:

$$t_1 = \frac{2d}{80}$$

بنابراین، سرعت متوسط برابر است با:

$$\overline{V} = \frac{displacement}{t} = \frac{d + 2 d }{(\frac{d}{60} + \frac{2d}{80})} = \frac{3d }{\frac{( 80 d + 26 \times 60)}{(60 \times 80)}} = \frac{34}{\frac{200 d}{4800}} = \frac{3d \times 4800}{200 d} = 72 \frac {km } { h }$$

به این نکته توجه داشته باشید که جسم همیشه روی خط مستقیم، به چپ یا راست حرکت نمی‌کند. به بیان دیگر، حرکت اجسام همیشه یک‌بعدی نیست. اجسام در دو یا سه بعد نیز حرکت می‌کنند. در ادامه، چند مثال در مورد حرکت دوبعدی اجسام و چگونگی محاسبه سرعت متوسط در دو بعد، حل می‌کنیم.

مثال چهارم

راننده‌ای با سرعت ۶۰ کیلومتر بر ساعت، ۱۲۰ کیلومتر به سمت جنوب و سپس با سرعت ۵۰ کیلومتر بر ساعت، ۱۵۰ کیلومتر به سمت شرق می‌رود.

1. تندی متوسط اتومبیل در کل مسیر چه مقدار است؟
2. بزرگی سرعت متوسط در کل مسیر حرکت را به‌دست آورید.

پاسخ

در این مثال، حرکت دو بعدی است. مسیر طی شده توسط اتومبیل به دو قسمت تقسیم می‌شود:

1. ابتدا، مسیر ۱۲۰ کیلومتری را با سرعت ثابت ۶۰ کیلومتر بر ساعت طی شده است.
2. در ادامه، مسیر ۱۵۰ کیلومتری با سرعت ۵۰ کیلومتر بر ساعت طی شده است.

زمان $$t_1$$ برای طی کردن مسیر ۱۲۰ کیلومتری با سرعت ثابت ۶۰ کیلومتر بر ساعت برابر است با:

$$t_1 = \frac{120}{60} = 2 h$$

زمان $$t_۲$$ برای طی کردن مسیر ۱۵۰ کیلومتری با سرعت ثابت ۵۰ کیلومتر بر ساعت برابر است با:

$$$$t_1 = frac{150}{50} = 3 h$$$$

بنابراین مدت زمان کل حرکت برابر ۵ ساعت است. برای محاسبه تندی و سرعت متوسط تنها کافی است مسافت و جابجایی را به‌دست آوریم.

قسمت ۱: در این قسمت، تندی متوسط اتومبیل را در کل مسیر حرکت به‌دست می‌آوریم:

$$S = \frac{ 120 km + 150 km km}{5 h} = \frac { 270 km } { 5 h } = 54 \frac{km}{h}$$

قسمت 2: در این قسمت، سرعت متوسط اتومبیل را در کل مسیر حرکت به‌دست می‌آوریم. برای انجام این کار ابتدا باید جابجایی را محاسبه کنیم. جابجایی، کمیتی برداری است. جهت این بردار از نقطه آغاز به نقطه پایان حرکت و بزرگی آن برابر طول بردارِ متصل‌کننده نقطه آغاز و پایان است. همان‌طور که در تصویر بالا دیده می‌شود، جابجایی برابر طول خط AC است. برای محاسبه طول این خط از قضیه فیثاغورث به صورت زیر استفاده می‌کنیم:

$$AC ^ 2 = 120 ^ 2 + 150 ^ 2 AC = \sqrt{14400 + 22500} = 30 \sqrt{41} km$$

با داشتن جابجایی کل و زمان، سرعت متوسط را به صورت زیر به‌دست می‌آوریم:

$$\overline{V} = \frac{ 30 \sqrt{ 41 }}{5 h} = 38. 4 \frac{km}{h}$$

مثال پنجم

اتومبیلی در مدت نیم ساعت، ۲۲ کیلومتر به سمت جنوب، ۱۲ کیلومتر به سمت غرب و ۱۴ کیلومتر به سمت شمال، حرکت می‌کند.

1. تندی متوسط اتومبیل چه مقدار است؟
2. جابجایی نهایی اتومبیل چه مقدار است؟
3. سرعت متوسط اتومبیل را به‌دست آورید.

پاسخ

مدت زمان کل حرکت اتومبیل برابر ۳۰ دقیقه یا نیم ساعت است.

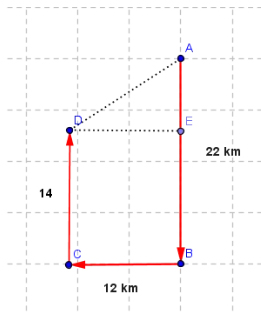
قسمت ۱: در این قسمت، تندی متوسط را به‌دست می‌آوریم.

$$S = \frac{ 22 km + 12 km + 14 km}{0.5 h} = \frac { 48 km } { 5 h } = 96 \frac{km}{h}$$

قسمت ۲: در این قسمت، جابجایی کل اتومبیل را به‌دست می‌آوریم. با توجه به تصویر نشان داده شده در بالا، جابجایی برابر طول خط AD، وتر مثلث DEA، است. برای محاسبه طول این خط از قضیه فیثاغورث به صورت زیر استفاده می‌کنیم:

$$AE = 22 - 14 = 8 km DA ^ 2 = AE ^ 2 + ED ^ @ = 8 ^ 2 + 12 ^ 2 = 64 +144 = 208 DA = \sqrt{208} = 4 \sqrt{ 13 } km$$

قسمت ۳: در این قسمت، سرعت متوسط اتومبیل را در کل مسیر حرکت به‌دست می‌آوریم.

$$\overline{V} = \frac{ 4 \sqrt{ 13 }}{0.5 h} = 28.8 \frac{km}{h}$$

مثال ششم

مردی مسیر نشان داده شده در تصویر زیر را در مدت زمان ۳۲۵۰ ثانیه پیموده است:

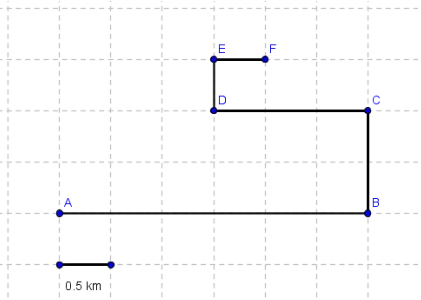
1. تندی متوسط را بر حسب متر بر ثانیه برای کل مسیر حرکت به‌دست آورید.
2. فرد چه مقدار جابجا شده است.
3. بزرگی سرعت متوسط را بر حسب متر بر ثانیه برای کل مسیر حرکت به‌دست آورید.

پاسخ

در ابتدا، تندی متوسط را برای کل مسیر به‌دست می‌آوریم. برای انجام این کار، ابتدا مسافت کل طی شده توسط فرد را به‌دست می‌آوریم. سپس، آن را بر زمان کل، تقسیم می‌کنیم. بر طبق تصویر نشان داده شده در بالا، فرد پنج مسیر مختلف را طی کرده است:

• نقطه آغاز حرکت نقطه A است. فرد از این نقطه، به اندازه ۳ کیلومتر به سمت شرق می‌رود و به نقطه B می‌رسد.
• از نقطه B، یک کیلومتر به سمت شمال می‌رود و به نقطه C می‌رسد.
• سپس، ۱/۵ کیلومتر به سمت غرب می‌رود و به نقطه D می‌رسد.
• از نقطه D، نیم کیلومتر به سمت شمال می‌رود و به نقطه E می‌رسد.
• در آخرین مسیر، از نقطه E، نیم کیلومتر به سمت شرق می‌رود و به نقطه F می‌رسد.

بنابراین، مسافت کل طی شده توسط فرد برابر ۶/۵ کیلومتر است. تندی متوسط در کل مسیر برابر است با:

$$S = \frac{ 3 km + 1 km + 1.5 km + 0.5 km + 0.5 km }{3250 s h} = \frac { 6.5 km km } { 3250 h } = \frac { 6500 m } { 3250 s} = 2 \frac{m}{s}$$

جابجایی برابر فاصله بین نقطه آغاز حرکت،‌ A، و نقطه پایان حرکت، F، است. برای محاسبه طول AF، از مثلث فرضی AFH و قضیه فیثاغورث استفاده می‌کنیم.

$$AF ^ 2 = FH ^ 2 + HA ^ 2 = 3 ^ 2 + 4 ^ 2 = 9 + 16 = 25 DA = \sqrt { 25} = 5 km$$

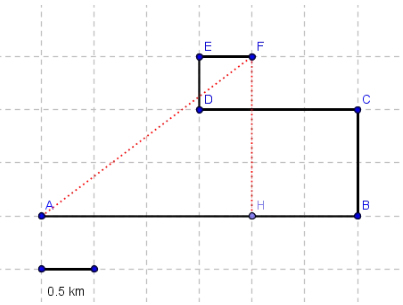
سرعت متوسط اتومبیل در کل مسیر حرکت برابر است با:

$$\overline{V} = \frac{ 5 km}{3250 s h} = \frac { 5000 m} { 3250 s } = 1.5 \frac{m}{s}$$

مثال هفتم

همان‌طور که در تصویر زیر نشان داده شده است، سنجابی به دنبال غذا می‌گردد. او ابتدا ۳ متر به سمت راست می‌دود. سپس ۱۰ متر به سمت چپ می‌رود و در پایان ۳ متر دیگر به سمت چپ می‌دود و غذاهای خود را جمع‌آوری می‌کند. اگر مدت زمان کل حرکت سنجاب برابر ۱۲ ثانیه باشد، سرعت و تندی متوسط او را به‌دست آورید.

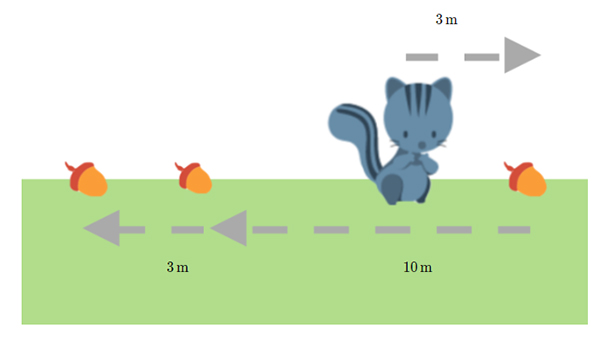
پاسخ

ابتدا مقدارهای مشخص و نامشخص در این مثال را تعیین می‌کنیم:

• اندازه و جهت جابجایی مشخص است:
  • ابتدا، سنجاب ۳ متر به سمت راست حرکت می‌کند. بنابراین جابجایی او برابر ۳+ متر است.
  • در ادامه، جهت حرکت خود را تغییر می‌دهد و ۱۰ متر به سمت چپ حرکت می‌کند، بنابراین جابجایی او برابر ۱۰- متر خواهد بود.
  • در پایان، ۳ متر دیگر به سمت چپ می‌دود. در نتیجه، جابجایی او برابر ۳- است.
• زمان کلِ حرکت سنجاب برابر ۱۲ ثانیه است.
• سرعت متوسط و تندی متوسط را باید به‌دست آوریم.

ابتدا سرعت متوسط را حساب می‌کنیم:

$$\overline{v} = \frac{\triangle x }{t} = \frac{3 m - 10 m - 3 m }{12 s} = \frac{-10 m}{12 s} = - 0.83 \frac {m} {s}$$

بنابراین، سرعت متوسط سنجاب برابر ۰/۸۳ متر بر ثانیه و جهت آن به سمت چپ است. چرا؟ زیرا، سرعت متوسط در راستای بردار جابجایی و هم‌جهت با آن است.

تندی متوسط برابر است با:

$$\overline{s} = \frac{distance }{t} = \frac{|3 | m + | - 10 | m + | - 3 | m }{12 s} = \frac{16 m}{12 s} = 1.3 \frac {m} {s}$$

 سرعت متوسط در حالت کلی

سرعت متوسط جسم را به صورت جابجایی انجام شده بر مدت زمان جابجایی، تعریف کردیم. در حالت کلی جسم با شتاب ثابت روی خط راست حرکت نمی‌کند، بلکه با شتاب متغیر در مسیری دلخواه حرکت می‌کند. در این حالت، سرعت متوسط به صورت زیر محاسبه می‌شود:

$$\overrightarrow{v }_ { average} = \frac{\overrightarrow{D}}{t}$$

از آنجا که سرعت‌ها، بردارهایی در جهت‌های متفاوت هستند و شتاب حرکت جسم ثابت نیست، از رابطه زیر نمی‌توانیم برای محاسبه سرعت متوسط استفاده کنیم:

$$\frac{\overrightarrow{v}_ 1 + \overrightarrow{v} _ 2}{2}$$

محاسبه سرعت متوسط با استفاده از نمودار سرعت-زمان

برای رسم نمودار سرعت برحسب زمان دو حالت را در نظر می‌گیریم:

1. حرکت با سرعت ثابت
2. حرکت با سرعت متغیر

حرکت با سرعت ثابت

در این حالت سرعت جسم در تمام طول حرکت ثابت است، بنابراین نمودار سرعت بر حسب زمان خطی افقی (موازی محور زمان) خواهد بود. به عنوان مثال، اگر جسمی با سرعت ثابت ۲۰ متر بر ثانیه روی خط مستقیمی حرکت کند، نمودار سرعت-زمان آن به صورت زیر خواهد بود.

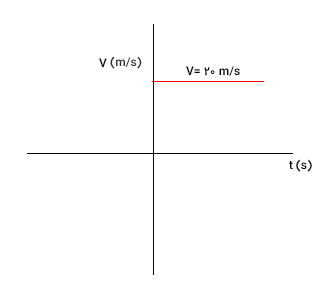
همان‌طور که در نمودار بالا دیده می‌شود، مقدار سرعت حرکت جسم در تمام لحظات یکسان و برابر ۲۰ متر بر ثانیه است. از این‌رو، مقدار سرعت متوسط نیز برابر ۲۰ متر بر ثانیه خواهد بود.

حرکت با سرعت متغیر

در حرکت با سرعت متغیر، همان‌گونه که از نامش مشخص است، سرعت حرکت جسم نسبت به زمان ثابت نیست و مقدار آن با گذشت زمان تغییر می‌کند. به عنوان مثال، راننده‌ای را در نظر بگیرید که اتومبیل خود را از حالت سکون به حرکت در می‌آورد، بنابراین، سرعت اتومبیل از صفر به مقدار مشخصی می‌رسد. سپس، راننده با همین سرعت حرکت می‌کند و هنگام نزدیک شدن به مقصد از سرعت خود می‌کاهد و در پایان، به طور کامل متوقف می‌شود. نمودار سرعت-زمان حرکت اتومبیل را چگونه می‌توان رسم کرد؟

برای رسم نمودار سرعت برحسب زمان این اتومبیل، فرض می‌کنیم افزایش و کاهش سرعت با آهنگ ثابتی انجام شده است (شتاب ثابت). حرکت اتومبیل از سه بخش تشکیل می‌شود:

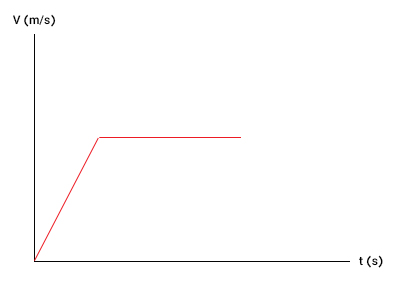
• بخش اول: در این قسمت، اتومبیل از حالت ساکن شروع به حرکت می‌کند. بنابراین، سرعت اولیه آن برابر صفر است. سپس، سرعت آن با آهنگ ثابتی شروع به افزایش می‌کند و به مقدار مشخص $$v$$ می‌رسد. افزایش سرعت با آهنگ ثابت نشان می‌دهد که نمودار سرعت زمان خط مستقیمی با شیب ثابت و مثبت است. از این‌رو، نمودار سرعت زمان در بخش اول حرکت اتومبیل، به صورت زیر رسم می‌شود. توجه به این نکته مهم است که شیب خط، برابر شتاب حرکت است.

• بخش دوم: در این قسمت، اتومبیل با سرعت ثابت به حرکت خود ادامه می‌دهد. بنابراین، نمودار سرعت برحسب زمان همانند بخش قبل، خطی افقی با شیب صفر خواهد بود.

• بخش سوم: در این قسمت، سرعت اتومبیل با آهنگ ثابت، شروع به کاهش می‌کند و به صفر می‌رسد. کاهش سرعت با آهنگ ثابت نشان می‌دهد که نمودار سرعت زمان خط مستقیمی با شیب ثابت و منفی است. از این‌رو، نمودار سرعت زمان در بخش سوم حرکت اتومبیل، به صورت زیر رسم می‌شود. توجه به این نکته مهم است که شیب خط، برابر شتاب حرکت است.

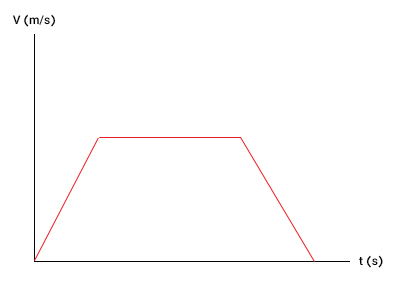
سوالی که ممکن است مطرح شود آن است که سرعت متوسط را چگونه می‌توان با استفاده از نمودار سرعت-زمان در حرکت با سرعت متغیر به‌دست آورد. برای انجام این کار، از نمودار اتومبیل که در بالا رسم کردیم، استفاده می‌کنیم. بخش اول حرکت را در نظر بگیرید. سرعت اتومبیل با آهنگ یا شتاب ثابت افزایش می‌یابد. برای به‌دست آوردن سرعت متوسط در بخش اول حرکت، دو نقطه را به دلخواه روی نمودار سرعت-زمان در بخش اول در نظر می‌گیریم:

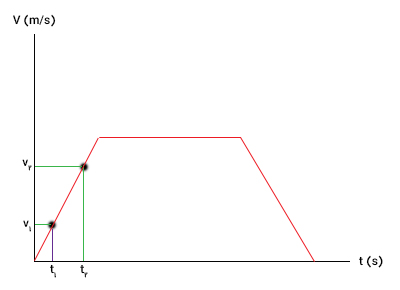
توجه به این نکته مهم است که سرعت‌های $$v_1$$ و $$v_2$$، سرعت‌های لحظه‌ای اتومبیل در زمان‌های $$t_1$$ و $$t_2$$ هستند. در ادامه، در مورد تفاوت سرعت متوسط با سرعت لحظه‌ای توضیح می‌دهیم. با داشتن سرعت‌های لحظه‌ای در دو زمان متفاوت، سرعت متوسط را می‌توان با استفاده از رابطه زیر به‌دست آورد:

$$\overline{v} = \frac{v_1 + v_2}{2}$$

به این نکته توجه داشته باشید که از رابطه بالا، تنها هنگامی می‌توانیم استفاده کنیم که جسم با شتاب ثابت، حرکت کند.

چه اطلاعاتی را می توان از نمودار سرعت-زمان به دست آورد ؟

با استفاده از نمودار سرعت-زمان می‌توانیم شتاب حرکت جسم و جابجایی آن را به‌دست آوریم.

شتاب در نمودار سرعت-زمان

شتاب حرکت ذره برابر شیب نمودار سرعت-زمان است و به صورت زیر به‌دست می‌آید:

$$a = \frac{v _ 2 - v_ 1}{t _ 2 - t _1}$$

اگر نمودار سرعت زمان خطی افقی و موازی محور زمان باشد، مقدار شتاب برابر صفر خواهد بود. به این حرکت، حرکت با سرعت ثابت گفته می‌شود. اگر نمودار سرعت-زمان، خطی مستقیم با شیب ثابت باشد، مقدار شتاب ثابت است. به این حرکت، حرکت با شتاب ثابت می‌گوییم. حرکت دیگری به نام حرکت با شتاب متغیر نیز وجود دارد. نمودار سرعت-زمان در این حرکت، خط مستقیم نیست.

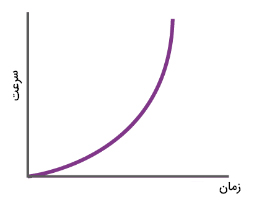
برای به‌دست آوردن شتاب با استفاده از نمودار بالا در زمان دلخواه t، باید خط مماسی در زمان t بر آن رسم کنیم. شیب خط مماس، شتاب لحظه‌ای را در زمان t به ما می‌دهد. شیب خط مماس بر نمودار بالا در هر لحظه از زمان، نسبت به زمان قبل یا بعد از آن تغییر می‌کند، بنابراین شتاب حرکت متغیر خواهد بود.

جابجایی در نمودار سرعت-زمان

برای به‌دست آوردن جابجایی ذره‌ای در فاصله زمانی مشخص، سطح زیر نمودار سرعت-زمان را در فاصله زمانی داده شده محاسبه می‌کنیم. به عنوان مثال، برای آن‌که جابجایی ذره را با استفاده از نمودار سرعت-زمان داده شده در بازه زمانی $$t_1$$ تا $$t_2$$ به‌دست آوریم، باید مساحت ذوزنقه را حساب کنیم.

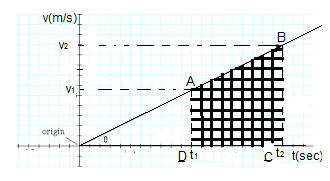
نکته: از آنجا که جابجایی جسم کمیتی برداری است، مساحت زیر محور زمان، منفی و بالای آن، مثبت است.

تفاوت سرعت متوسط و سرعت لحظه ای چیست ؟

در مطالب بالا با تعریف سرعت متوسط و تفاوت آن با تندی متوسط آشنا شدیم. در این بخش، در مورد تفاوت سرعت متوسط و لحظه‌ای صحبت می‌کنیم. سرعت متوسط را به صورت جابجایی بر مدت زمان جابجایی تعریف کردیم. سرعت متوسط هر جسمی همواره کوچک‌تر یا برابر تندی متوسط است. دلیل این موضوع به تفاوت مفهوم مسافت و جابجایی برمی‌گردد. مسافت، همواره افزایشی است، اما جهت جابجایی می‌تواند تغییر کند و اندازه آن نیز ممکن است افزایش یا کاهش یابد.

$$\overline{v} = \frac{x_2 - x_1}{t_2 - t_1} = \frac{\triangle x}{\triangle t}$$

در رابطه بالا:

• $$x_ 1$$ مکان اولیه ذره است.
• $$x_ 2$$ مکان نهایی ذره است.
• $$t_1$$ زمان را در مکان اولیه ذره نشان می‌دهد.
• $$t_2$$ زمان را در مکان نهایی ذره نشان می‌دهد.

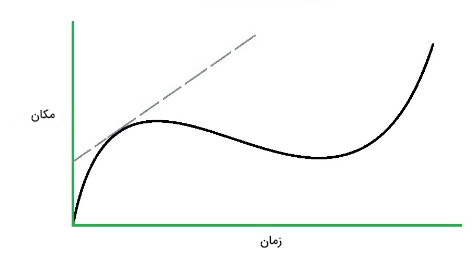
همچنین، در مورد چگونگی محاسبه سرعت متوسط با استفاده از نمودار سرعت-زمان، صحبت کردیم. توجه به این نکته مهم است که سرعت متوسط را می‌توان با استفاده از نمودار مکان-زمان نیز به‌دست آورد. سرعت متوسط به صورت شیب خط متصل‌کننده دو مکان، در نمودار مکان-زمان تعریف می‌شود. بنابراین، برای به‌دست آوردن سرعت متوسط از روی نمودار مکان زمان، دو نقطه روی نمودار انتخاب کنید و آن‌ها را توسط خطی مستقیم به یکدیگر متصل کنید. شیب خط برابر سرعت متوسط است.

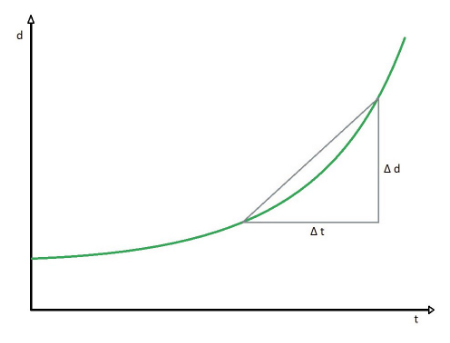
سرعت متوسط، مشابه میانگین گرفتن از سرعت نسبت به زمان است:

$$v_ {avg} = \frac{1}{t _ 2 - t_ 1} int_{ t _ 1}^{t _ 2 } v (t ) d t$$

هنگامی که بازه زمانی $$\triangle t$$ بسیار کوچک شود یا زمان $$t_2$$ به زمان $$t_1$$ نزدیک شود، سرعت متوسط به سرعت لحظه‌ای تبدیل می‌شود. به بیان دیگر، سرعت لحظه‌ای، حد سرعت متوسط به هنگام میل کردن $$\triangle t$$ به سمت صفر است. سرعت لحظه‌ای ممکن است از حاصل‌ضرب تندی جسم در جهت حرکت آن در زمان نیز به‌دست آید. اگر جسمی با سرعت ثابت حرکت کند، سرعت متوسط و سرعت لحظه‌ای آن با یکدیگر برابر هستند.

$$v ( t ) = lim_{\triangle t \rightarrow 0} \frac{\triangle x}{\triangle t} = \frac{\text{d}x}{\text{d}t}$$

در رابطه فوق:

• $$v ( t)$$ سرعت لحظه‌ای جسم در زمان t است.
• $$x$$ جابجایی جسم را نشان می‌دهد.
• $$t$$ نشان‌دهنده زمان است.
• $$\triangle t$$ فاصله زمانی بسیار کوچکی است که به سمت صفر میل می‌کند.

شیب خط مماس بر نمودار مکان-زمان در هر لحظه از زمان برابر سرعت لحظه‌ای در آن لحظه است.

تفاوت سرعت لحظه‌ای و متوسط به طور خلاصه در جدول زیر نشان داده شده است.

مثال ۱

مکان ذره‌ای برحسب زمان به صورت زیر داده شده است:

$$x (t ) = 2.0 t + 0.7 t ^ 3$$

سرعت لحظه‌ای را در زمان ۳/۰ ثانیه به‌دست آورید. سرعت متوسط ذره در فاصله زمانی بین ۳ تا ۵ ثانیه، چه مقدار است؟

پاسخ

مکان ذره بر حسب زمان به صورت زیر داده شده است:

$$x (t ) = 2.0 t + 0.7 t ^ 3$$

ابتدا، سرعت لحظه‌ای را به‌دست می‌آوریم. برای به‌دست آوردن سرعت لحظه‌ای در زمان ۳ ثانیه، از مکان نسبت به زمان مشتق می‌گیریم:

$$v ( t ) = lim_{\triangle t \rightarrow 0} \frac{\triangle x}{\triangle t} = \frac{\text{d}x}{\text{d}t} v ( t) = \frac{\text{d}}{\text{d}t} ( 2 t + 0.7 t ^ 3) = 2 + 2.1 t ^ 2$$

سرعت لحظه‌ای در زمان سه ثانیه برابر است با:

$$v ( t = 3 s) = 2 + 2.1 ( 3 ) ^ 2 = 20.9 \frac {m} {s}$$

برای به‌دست آوردن سرعت متوسط بین ۳ تا ۵ ثانیه، ابتدا مکان‌ جسم را در این زمان‌ها به‌دست می‌آوریم و در رابطه مربوط به سرعت متوسط قرار می‌دهیم:

مکان در زمان ۳ ثانیه:

$$x ( t = 3 s ) = 2.0 \times 3 + 0.7 ( 3 )^ 3 = 24.9 m$$

مکان در زمان ۵ ثانیه:

$$x ( t = 5 s ) = 2.0 \times 5 + 0.7 ( 5 )^ 3 = 97.5 m$$

با داشتن مکان‌ ذره در دو زمان ۳ و ۵ ثانیه، سرعت متوسط را به صورت زیر به‌دست می‌آوریم:

$$\overline{v} = \frac{x_2 - x_1}{t_2 - t_1} = \frac{\triangle x}{\triangle t} \overline{v} = \frac{97.5 - 24.9}{5 - 3} = 36.3 \frac { m } {s }$$

مثال دوم

توپی را از بالای ساختمانی به طور مستقیم به سمت بالا پرتاب می‌کنیم. ارتفاع توپ نسبت به زمین بر حسب زمان به صورت زیر بیان می‌شود:

$$s (t ) = -4.9 t ^ 2 + 98 t + 200$$

1. ارتفاع ساختمان را به‌دست آورید.
2. سرعت اولیه توپ چه مقدار است؟
3. سرعت لحظه‌ای توپ در زمان ۵ ثانیه چه مقدار است؟
4. سرعت متوسط توپ در بازه زمانی ۴ تا ۶ ثانیه و ۴/۹ تا ۵/۱ ثانیه، چه مقدار است؟
5. توپ پس از چه مدتی به زمین می‌رسد؟
6. سرعت توپ قبل از برخورد به زمین چه مقدار است؟
7. توپ، چه مدت پس از پرتاب به بالاترین ارتفاع می‌رسد؟
8. بیشینه ارتفاع توپ از سطح زمین را به‌دست آورید.

پاسخ

فرض کنید توپی را از بالای پشت‌بام ساختمانی به سمت بالا پرتاب می‌کنید. توپ پس از رسیدن به ارتفاع مشخصی (ارتفاع بیشینه)، به سمت زمین برمی‌گردد. حرکت توپ به صورت شماتیک در تصویر زیر نشان داده شده است. ارتفاع توپ از سطح زمین با تابع $$s(t)$$ نشان داده می‌شود.

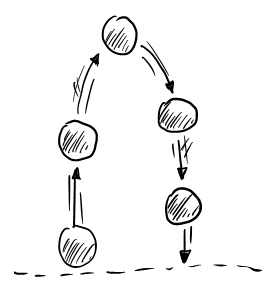
قسمت ۱: در این قسمت، ارتفاع ساختمان را به‌دست می‌آوریم. محل پرتاب را مبدأ در نظر می‌گیریم و آن را با A نشان می‌دهیم. همچنین، ارتفاع بیشینه با B و محل برخورد توپ با زمین را با C، نشان داده می‌شوند.

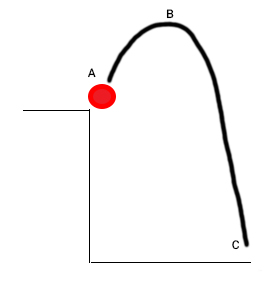
زمان در مکان A برابر صفر است. برای به‌دست آوردن ارتفاع ساختمان‌، باید مقدار s را در زمان صفر به‌دست آوریم.

$$s( t = 0 ) = - 4.9 \times ( 0 ) ^ 2 + 98 \times 0 + 200 s (0) = 200 m$$

قسمت ۲: برای به‌دست آوردن سرعت اولیه توپ، باید از مکان نسبت به زمان مشتق بگیریم و سپس زمان را برابر صفر قرار دهیم:

$$v ( t) = \frac{\text{d}s}{\text{d}t} = \frac{\text{d}}{\text{d}t} ( - 4.9 t ^ 2 + 98 t + 200 ) = -9.8 t + 98 v ( 0 ) = -9.8 ( 0 ) + 98 = 98$$

قسمت 3: در قسمت قبل، رابطه سرعت بر حسب زمان را به‌دست آوردیم. برای محاسبه سرعت لحظه‌ای در زمان ۵ ثانیه، تنها کافی است که به جای زمان، ۵ بگذاریم و مقدار سرعت را به‌دست آوریم:

$$v ( t) = -9.8 t + 98 v ( 5 ) = -9.8 ( 5 ) + 98 = 49 \frac {m} {s }$$

عدد به‌دست آمده برای سرعت چه چیزی را نشان می‌دهد؟ در این مساله حرکت به سمت بالا را مثبت و حرکت به سمت پایین را منفی در نظر می‌گیریم. توپ ابتدا به سمت بالا پرتاب می‌شود و پس از رسیدن به نقطه B، به سمت زمین برمی‌گردد. بنابراین لحظه‌ای که توپ بین نقطه‌های A و B قرار دارد، سرعت آن به سمت بالا و مثبت است. همچنین، لحظه‌ای که توپ بین نقطه‌های B و C قرار دارد، سرعت آن منفی و به سمت پایین خواهد بود. در لحظه ۵ ثانیه، سرعت توپ مثبت است. بنابراین، توپ در این لحظه بین نقطه‌های A و B قرار دارد و به سمت بالا حرکت می‌کند. در نتیجه، زمانی که توپ به نقطه B می‌رسد از ۵ ثانیه بیشتر است.

قسمت ۴: در این قسمت باید سرعت متوسط توپ را در دو بازه زمانی متفاوت به‌دست آوریم. برای محاسبه سرعت متوسط، از تابع مکان برحسب زمان استفاده می‌کنیم. ابتدا، مکان توپ را در زمان‌های ۴ و ۶ ثانیه به‌دست می‌آوریم:

$$s ( t ) = - 4.9 t ^ 2 + 98 t + 200 s (t = 4 s ) = - 4.9 \times ( 4)^ 2 + 98 \times 4 + 200 = 513. 6$$

$$s (t = 6 s ) = - 4.9 \times ( 6)^ 2 + 98 \times 6 + 200 = 611 . 6$$

مکان‌های به‌دست آمده را در رابطه سرعت متوسط قرار می‌دهیم و مقدار آن را در بازه زمانی ۴ تا ۶ ثانیه به‌دست می‌آوریم:

$$\overline{ v } = \frac{s ( 6 ) - s ( 4 )}{6 - 4 } = \frac{611.6 - 513. 6}{2 } = \frac{98}{2} = 49 \frac {m} { s}$$

در ادامه، مکان توپ را در زمان‌های 4.9 و 5.1 ثانیه به‌دست می‌آوریم:

$$s ( t ) = - 4.9 t ^ 2 + 98 t + 200 s (t = 4 .9 s ) = - 4.9 \times ( 4 . 9)^ 2 + 98 \times 4.9 + 200 = 562.6 m s (t = 5.1 s ) = - 4.9 \times ( 5.1 )^ 2 + 98 \times 5.1 + 200 = 572.35 m$$

مکان‌های به‌دست آمده را در رابطه سرعت متوسط قرار می‌دهیم و مقدار آن را در بازه زمانی ۴/۹ تا ۵/۱ ثانیه به‌دست می‌آوریم:

$$\overline{ v } = \frac{s ( 5.1 ) - s ( 4.9 )}{6 - 4 } = \frac{572.35 - 562. 6 }{0.2 } = \frac{98}{2} = 48.75 \frac {m} { s}$$

همان‌طور که مشاهده می‌کنید، سرعت متوسط در دو بازه زمانی بسیار به هم نزدیک هستند.

قسمت ۵: در این قسمت، مدت زمان رسیدن توپ به زمین، یعنی نقطه C، را به‌دست می‌آوریم. در نقطه C، ارتفاع توپ از سطح زمین برابر صفر است. بنابراین، برای آن‌که زمان رسیدن توپ به زمین را به‌دست آوریم، s را برابر صفر قرار می‌دهیم:

$$s ( t ) = - 4.9 t ^ 2 + 98 t + 200 = 0$$

معادله بالا، معادله درجه دو برحسب t است. بنابراین، آن را با استفاده از روش دلتا حل می‌کنیم.

$$t = \frac{-98 pmsqrt{(98)^2-4(-4.9)(200)}}{9.8} =\frac{ 98 \pm \sqrt{13525}}{98} \frac{98 \pm 116.3}{9.8}$$

با حل معادله مکان برحسب زمان، دو جواب برای زمان به‌دست می‌آید. با توجه به آن‌که زمان منفی در فیزیک معنایی ندارد، آن را حذف می‌کنیم. بنابراین، زمان رسیدن توپ به زمین برابر 21/9 ثانیه است.

قسمت ۶: برای به‌دست آوردن سرعت توپ قبل از برخورد آن به زمین، از معادله سرعت برحسب زمان استفاده می‌کنیم:

$$v ( t ) = -9.8 t + 98$$

زمان رسیدن توپ به زمین برابر ۲۱/۹ ثانیه است. از آنجا که سرعت توپ را درست در لحظه قبل از برخورد آن به زمین می‌خواهیم، زمان را برابر ۲۱/۸۷ ثانیه می‌گیریم و آن را در رابطه سرعت برحسب زمان قرار می‌دهیم:

$$v ( 21.87 s ) = -9.8 \times 21.87 + 98 v ( 21.87 s ) = -116 \frac {m} {s }$$

سرعت توپ، منفی است. بنابراین، جهت آن به سمت پایین خواهد بود.

قسمت ۷: سرعت توپ در نقطه B یا ارتفاع بیشینه برابر صفر است. بنابراین، برای به‌دست آوردن زمان رسیدن توپ به ارتفاع بیشینه، از معادله سرعت برحسب زمان استفاده می‌کنیم و مقدار سرعت را در آن برابر صفر قرار می‌دهیم.

$$v ( t ) = -9.8 t + 98 0 = -9.8 t + 98 9.8 t = 98 t = \frac{98}{9.8} = 10 s$$

قسمت ۸: در قسمت آخر این مثال، ارتفاع بیشینه را از سطح زمین به‌دست می‌آوریم. به بیان دیگر، فاصله نقطه B را باید از زمین محاسبه کنیم. در قسمت ۷، زمان رسیدن توپ به ارتفاع بیشینه را برابر ۱۰ ثانیه به‌دست آوردیم. بنابراین، این زمان را در رابطه $$s ( t )$$ قرار می‌دهیم.

$$s ( t ) = - 4.9 t ^ 2 + 98 t + 200 s (t = 10 s ) = - 4.9 \times ( 10)^ 2 + 98 \times 10 + 200 =690 m$$

مثال سوم

مکان ذره‌ای با استفاده از معادله $$x ( t) = 4 t ^ 2 + 5 t - 6$$ توصیف می‌شود.

1. سرعت لحظه‌ای ذره را ۳ ثانیه پس از شروع حرکت به‌دست آورید.
2. سرعت متوسط ذره در فاصله زمانی ۲ تا ۳ ثانیه چه مقدار است؟

پاسخ

در این مثال معادله مکان برحسب زمان ذره داده شده است. در قسمت یک، سرعت لحظه‌ای را سه ثانیه پس از شروع حرکت به‌دست می‌آوریم. برای به‌دست آوردن سرعت لحظه‌ای در زمان سه ثانیه، از تابع مکان برحسب زمان مشتق می‌گیریم:

$$v ( t) = \frac{\text{d}x}{\text{d}t} = \frac{\text{d}}{\text{d}t} ( 4 t ^ 2 + 5 t - 6) = 8t + 5$$

سرعت لحظه‌ای در زمان ۳ ثانیه برابر است با:

$$v ( t = 3 s) = 8 ( 3 ) + 5 = 24 + 5 = 29 \frac{m}{s}$$

در قسمت دوم مثال، سرعت متوسط را در بازه زمانی ۲ تا ۳ ثانیه به‌دست می‌آوریم. برای انجام این کار، ابتدا جابجایی ذره را در این بازه زمانی محاسبه می‌کنیم:

مکان ذره در زمان ۲ ثانیه:

$$x ( t = 2 s) = 4 ( 2 ) ^ 2 + 5 (2) - 6 = 20 m$$

مکان ذره در زمان 3 ثانیه:

$$x ( t = 3 s) = 4 ( 3 ) ^ 2 + 5 (3) - 6 = 45 m$$

جابجایی کل ذره در بازه زمانی ۲ تا ۳ ثانیه برابر است با:

$$\triangle x = x ( 3 ) - x ( 2 ) = 45 -20 = 25 m$$

با قرار دادن جابجایی در رابطه مربوط به سرعت متوسط داریم:

$$\overline{v} = \frac{x_2 - x _1 }{t _2 - t _1 } = \frac{25}{3 - 2} = 25 \frac { m } { s }$$

پرسش 1: آیا سرعت متوسط را می‌توان با استفاده از رابطه $$\frac { v_1 + v_ 2} { 2 }$$ به‌دست آورد؟

پاسخ: برای پاسخ به این پرسش، سرعت متوسط را با استفاده از فرمول $$\frac { v_1 + v_ 2} { 2 }$$ به‌دست می‌آوریم و مقدار آن را با مقدار به‌دست آمده از قسمت دوم، مقایسه می‌کنیم. $$v_1$$ سرعت در زمان ۲ ثانیه و $$v_2$$ سرعت در زمان ۳ ثانیه است.

محاسبه سرعت در زمان ۲ ثانیه:

$$v( t = 2 s) = 8 ( 2) + 5 = 21 \frac { m } { s}$$

محاسبه سرعت در زمان 3 ثانیه:

$$v( t = 3 s) = 8 ( 3) + 5 = 29 \frac { m } { s}$$

مقدارهای به‌دست آمده را در رابطه $$\frac { v_1 + v_ 2} { 2 }$$ قرار می‌دهیم:

$$\overline{v} = \frac { v_1 + v_ 2} { 2 } = \frac{21 + 29}{2} = \frac{50}{2} = 25 \frac{m}{s}$$

سرعت متوسط به‌دست آمده از فرمول $$\frac { v_1 + v_ 2} { 2 }$$ با سرعت متوسط به‌دست آمده در قسمت دوم، با یکدیگر برابر شدند. چرا؟ دلیل این موضوع به ثابت بودن شتاب حرکت مربوط می‌شود. در مطالب بالا گفتیم هرگاه ذره‌ای با شتاب ثابت حرکت کند، سرعت متوسط را می‌توان با استفاده از رابطه $$\frac { v_1 + v_ 2} { 2 }$$ به‌دست آورد.

مثال چهارم

سرعت جسمی برحسب زمان با استفاده از تابع $$v ( t ) = 2 t ^ 2 + 7 t - 4$$ توصیف می‌شود. سرعت لحظه‌ای در زمان ۲ ثانیه و سرعت متوسط در بازه زمانی ۳ تا ۴ ثانیه را به‌دست آورید. آیا سرعت متوسط را می‌توان با استفاده از رابطه $$\frac { v_1 + v_ 2} { 2 }$$ محاسبه کرد؟

پاسخ

برای به‌دست آوردن سرعت لحظه‌ای در زمان ۲ ثانیه، تنها کافی است در رابطه سرعت برحسب زمان، به جای زمان، ۲ قرار دهیم:

$$v ( t = 2 s ) = 2 ( 2 ) ^ 2 + 7 ( 2) - 4 = 18 \frac { m} { s}$$

برای آن‌که بتوانیم سرعت متوسط را محاسبه کنیم، ابتدا باید تابع مکان برحسب زمان را به‌دست آوریم. برای به‌دست آوردن تابع مکان، از تابع سرعت برحسب زمان، انتگرال می‌گیریم:

$$x ( t) = \int x(t) d t = \int ( 2 t ^ 2 + 7 t - 4 ) d t = \frac{2}{3} t ^ 3 + \frac{7}{2} t ^ 2 - 4 t + C$$

در رابطه فوق، C ثابت انتگرال‌گیری است.

مکان ذره در زمان ۳ ثانیه:

$$x ( t) = \frac{2}{3} t ^ 3 + \frac{7}{2} t ^ 2 - 4 t + C x ( 3 ) = \frac{2}{3} (3 ) ^ 3 + \frac{7}{2} ( 3 )^ 2 - 4 ( 3 ) + C =37.5 + C$$

مکان ذره در زمان 4 ثانیه:

$$x ( t) = \frac{2}{3} t ^ 3 + \frac{7}{2} t ^ 2 - 4 t + C x ( 4 ) = \frac{2}{3} (4 ) ^ 3 + \frac{7}{2} ( 4 )^ 2 - 4 ( 4 ) + C =82.7 + C$$

جابجایی ذره در بازه زمانی ۳ تا ۴ ثانیه برابر است با:

$$\triangle x = x_ 2 - x_ 1 = 82.7 - 37.5 = 45.2 m$$

سرعت متوسط ذره در این بازه زمانی برابر است با:

$$\overline { v} = \frac {\triangle x } { t} = \frac { 45.2 m } { 4 - 3 } = 45.2 \frac { m } {s }$$

توجه به این نکته مهم است که سرعت متوسط ذره را نمی‌توان با استفاده از رابطه $$\frac { v_1 + v_ 2} { 2 }$$ به‌دست آورد، زیرا شتاب ذره ثابت نیست و با زمان تغییر می‌کند. شتاب حرکت برابر مشتق سرعت نسبت به زمان است:

$$a ( t ) = \frac{\text{d}v}{\text{d}t } = \frac{\text{d}}{\text{d}t } (2 t ^ 2 + 7 t - 4) = 4 t + 7$$

همان‌طور که در رابطه بالا دیده می‌شود، شتاب به زمان وابسته است و با تغییر زمان، مقدار آن نیز تغییر می‌کند. بنابراین، برای محاسبه سرعت متوسط نمی‌توانیم از رابطه $$\frac { v_1 + v_ 2} { 2 }$$ استفاده کنیم.

مثال پنجم

رابطه سرعت بر حسب زمان مثال چهارم را در نظر بگیرید. سرعت در چه زمان‌هایی صفر، مثبت و منفی است؟

پاسخ

برای آن‌که بدانیم سرعت ذره در چه زمان‌هایی صفر، مثبت یا منفی است، معادله سرعت برحسب زمان را با روش دلتا حل می‌کنیم.

$$v ( t ) = 2 t ^ 2 + 7 t - 4$$

در این معادله:

• $$a = 2$$
• $$b = 7$$
• $$c = - 4$$

$$t _ 1 \, t _ 2 = \frac{-bpmsqrt{b^2-4ac}}{2a} t _ 1 \, t _ 2 = \frac{-(7)pmsqrt{(7 )^2-4( 2 ) ( - 4 )}}{2 ( 2 ) } t _ 1 \, t _ 2 = \frac{- 7 \pm 9}{4} t_ 1 = - 4 s \, t _ 2 = \frac{1}{2} s$$

با توجه به آن‌که زمان منفی در فیزیک معنایی ندارد، سرعت در زمان ۰/۵ ثانیه برابر صفر می‌شود. در ادامه، با رسم نمودار سرعت برحسب زمان، مقدارهای منفی و مثبت سرعت را به‌دست می‌آوریم.

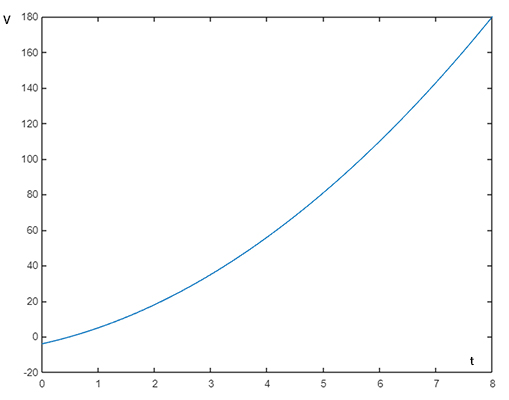
با توجه به نمودار رسم شده، سرعت برای زمان‌های بزرگ‌تر از ۰/۵ ثانیه مثبت و در بازه زمانی صفر تا ۰/۵ ثانیه منفی است. به این نکته توجه داشته باشید که نمودار سرعت-زمان برای زمان‌های منفی رسم نشده است.

سوالات رایج در مورد سرعت متوسط

در مطالب بالا در مورد سرعت متوسط و تفاوت آن با تندی متوسط صحبت کردیم. در ادامه به چند پرسش مهم در مورد سرعت متوسط پاسخ می‌دهیم.

سرعت متوسط را چگونه به دست می‌ آوریم ؟

برای محاسبه سرعت متوسط، در گام نخست باید جابجایی کل جسم در طول حرکت را به‌دست آوریم. به نمودار زیر دقت کنید، ذره‌ای را در نظر بگیرید که مسافت $$d_1$$ را در مدت زمان $$t _ 1$$، مسافت $$d_2$$ را در مدت زمان $$t _ 2$$، مسافت $$d_3$$ را در مدت زمان $$t _ 3$$، طی می‌کند. همان‌طور که در نمودار زیر ملاحظه می‌کنید، مسافت‌های طی شده در یک راستا نیستند، بنابراین $$d _ 1 + d _ 2 + d_3$$ برابر مسافت کل، و نه جابجایی کل، است. برای به‌دست آوردن جابجایی کل، تصویر $$d_2$$ و $$d_3$$ را در امتداد $$d_1$$ به‌دست می‌آوریم و آن‌ها را با $$d_1$$ جمع می‌کنیم.

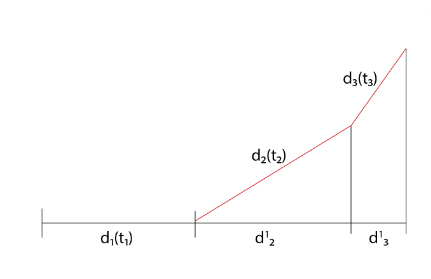
در نتیجه، سرعت متوسط به صورت زیر نوشته می‌شود:

$$v _ {av} = \frac{d_1 + d_2^1 + d_3^1}{t_1 + t_2+ t _3 }$$

سرعت متوسط چه کمیتی است ؟

سرعت متوسط کمیتی برداری است و اندازه و جهت دارد. سرعت متوسط در راستای بردار جابجایی است.

سرعت متوسط زاویه ای چیست ؟

تاکنون، در مورد سرعت متوسط در حرکت‌های خطی، صحبت کردیم. جسم در حرکت خطی روی خط مستقیم، به سمت چپ یا راست حرکت می‌کند. توجه به این نکته مهم است که حرکت اجسام بسیاری روی خط مستقیم نیست. به عنوان مثال، ماهواره روی مدار دایره‌ای به دور زمین می‌چرخد. در حرکت دایره‌ای، به جای سرعت خطی، از عبارت سرعت زاویه‌ای استفاده می‌کنیم. به زاویه طی شده توسط جسم در مسیر دایره‌ای در واحد زمان، سرعت زاویه‌ای ($$\omega$$) گفته می‌شود. جهت این سرعت ساعتگرد یا پادساعتگرد است:

$$\omega = \frac {\theta} { t}$$

در رابطه بالا، $$\theta$$ زاویه طی شده توسط جسم در زمان $$t$$ است.

سرعت متوسط چه زمانی با سرعت لحظه ای برابر است ؟

سرعت متوسط در حرکت با سرعت ثابت، با سرعت لحظه‌ای برابر است.

جمع‌بندی

در این مطلب، سرعت متوسط را به زبان ساده توضیح دادیم و تفاوت آن با تندی متوسط را بیان کردیم. همچنین، در مورد نحوه محاسبه سرعت متوسط با استفاده از نمودار سرعت-زمان صحبت کردیم. در حالت کلی، سرعت متوسط از تقسیم جابجایی بر زمان جابجایی به‌دست می‌آید. از آنجا که جابجایی کمیتی برداری است، سرعت متوسط نیز کمیتی برداری و هم‌جهت با بردار جابجایی خواهد بود.