ریسک نسبی در مدل آماری – محاسبه و کاربردها
یکی از روشهای اندازهگیری اثر یک متغیر مستقل روی متغیر وابسته در مدلهای آماری، محاسبه «ریسک نسبی» (Relative Risk) است. به این ترتیب با توجه به احتمال رخداد یک پیشامد در یک گروه نسبت به گروه دیگر ریسک نسبی مورد محاسبه قرار میگیرد. در این نوشتار با ریسک نسبی در مدل آماری، شیوه محاسبه و کاربردهای آن آشنا خواهیم شد.
به عنوان مقدمه و زمینهای برای آشنایی با اصطلاحات این مطلب، بهتر است جدول توافقی و کاربردهای آن در SPSS — از صفر تا صد و رگرسیون لجستیک چند جمله ای (Multinomial Logistic Regression) — مفاهیم و کاربردها را مطالعه کنید. همچنین خواندن مطلب رگرسیون لجستیک (Logistic Regression) — مفاهیم، کاربردها و محاسبات در SPSS و معیار ارزیابی BIC در مدل های احتمالی — از صفر تا صد نیز خالی از لطف نیست.
ریسک نسبی در مدل آماری
از ریسک نسبی برای تجزیه و تحلیل آماری دادههای تجربی و آزمایشگاهی (Experimental Data Analysis)، «مطالعات گروهها» (Cohort Study) و همچنین «مقایسههای دو طرفه» (Cross-sectional Study) استفاده میشود.
برای مثال اگر بخواهیم مقایسهای بین ریسک نتیجه منفی از یک روش درمانی را با روش بدون درمان بسنجیم، از ریسک نسبی استفاده میکنیم. همچنین اگر لازم باشد اثر مصرف سیگار را در بین بیمارانی که دچار سرطان ریه شدهاند اندازهگیری کنیم، از ریسک نسبی کمک میگیریم. به این ترتیب میتوانیم نشان دهیم که ریسک ابتلا به سرطان ریه نزد کسانی که سیگار مصرف میکنند نسبت به غیرسیگاریها چقدر است.
توجه داشته باشید که ریسک نسبی، تنها در یک گروه سنجیده نمیشود، بلکه از آن برای مقایسه شانس رخداد یک پیشامد در دو گروه متفاوت استفاده میشود.

شیوه محاسبه ریسک نسبی
ریسک نسبی همانطور که از اسمش پیدا است به صورت یک نسبت یا کسر مشخص و محاسبه میشود. در نتیجه یک بخش از محاسبه ریسک نسبی، مربوط به صورت کسر و بخش دیگر، مخرج آن را تشکیل میدهد. در این حالت صورت کسر مختص به گروهی است که تحت یک تیمار یا یک عامل قرار گرفتهاند. احتمال رخداد یک پیشامد خاص در چنین گروهی را در صورت کسر ریسک نسبی قرار میدهیم. مخرج کسر نیز احتمال رخداد همان پیشامد در گروهی است که تحت تاثیر آن عامل قرار نداشتهاند.
برای مثال در بررسی بیمارانی که به سرطان ریه مبتلا شدهاند، اگر بخواهیم ریسک نسبی ابتلا به سرطان ریه (پیشامد) را در دو گروه مختلف سیگاری (کسانی که در معرض یک تیمار خاص هستند) و غیر سیگاریها (کسانی که در معرض این تیمار نیستند) مشخص کنیم، کافی است احتمال داشتن سرطان ریه در گروه سیگاریها را به احتمال داشتن سرطان ریه در گروه غیرسیگاری، تقسیم کنیم.
به این ترتیب میتوانیم ریسک نسبی (Relative Risk) که با نماد نشان داده میشود را شبیه و مانند «نسبت بختها» (Odds Ratio) به صورت نسبت دو احتمال در نظر بگیریم. البته توجه داشته باشید که نسبت بختها با ریسک نسبی متفاوت است. این موضوع را در قسمتهای بعدی همین متن، مورد بررسی قرار میدهیم.
رابطه ۱
با توجه به رابطه ۱ و مقادیر مختلفی که خواهد داشت، عبارت زیر را در نظر میگیریم:
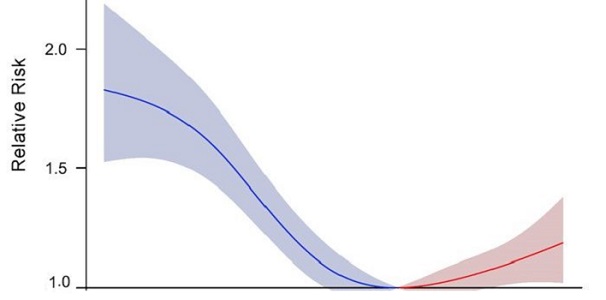
- اگر ، آنگاه گروهها نسبت به پیشامد تاثیرپذیر نیستند.
- اگر ، آنگاه ریسک پیشامد در گروهی که در معرض تیمار قرار دارند، کاهشی است.
- اگر ، آنگاه ریسک پیشامد در گروهی که در معرض تیمار قرار دارند، افزایشی است.
مثال ۱: فرض کنید که ۱۷٪ سیگاریها، دچار سرطان ریشه شده در حالیکه فقط ۱٪ از غیرسیگاریها این بیماری را دارند. به این ترتیب ریسک نسبی سرطان ریه نزد سیگاریها نسبت به غیرسیگاریها برابر است با:
این امر به این معنی است که ریسک ابتلا به سرطان در سیگاریها ۱۷ برابر غیرسیگاریها است. یا از بین ۱۰۰ سیگاری، ۱۷ نفر به سرطان مبتلا شده در حالیکه این عدد در غیرسیگاریها فقط ۱ نفر است.
مثال ۲: در یک طرح تحقیقی برای نشان دادن اثر جانبی یک مکمل غذایی، از 150 داوطلب استفاده شده است. در این بین، 56 نفر از آنها مکمل غذایی را دریافت کردهاند، که ۱۴ نفر از آنها از درد معده رنج میبرند و بقیه (42 نفر) مشکل معده ندارند.
به این ترتیب احتمال داشتن درد معده (A) در گروه مصرف کننده مکمل غذایی (B) برابر است با:
از طرفی فقط ۲ نفر از بقیه (یعنی 85 نفری که مکمل غذایی دریافت نکردهاند) درد معده دارند. به این ترتیب احتمال داشتن درد معده (A در گروهی که مکمل غذایی مصرف نکردهاند ('B) نیز به صورت زیر خواهد بود.
بنابراین ریسک نسبی داشتن درد معده بعد از مصرف مکمل غذایی نسبت به کسانی که مکمل مصرف نکردهاند، برابر است با:
به این ترتیب مشخص است که مصرف مکمل غذایی، ریسک داشتن درد معده را افزایش میدهد.
مثال ۳: در یک طرح تحقیقی مشخص شده است که فقط 40٪ افرادی که به طور منظم ورزش میکنند، دچار اضافه وزن هستند. در مقابل ۷۰٪ کسانی که ورزش یا فعالیت بدنی منظم ندارند، دچار اضافه وزن میشوند. به این ترتیب ریسک نسبی داشتن اضافه وزن (A) در بین کسانی که ورزش میکنند (B) نسبت به افرادی که فعالیت بدنی ندارند ('B) به صورت زیر محاسبه میشود.
در نتیجه ریسک داشتن اضافه وزن در بین کسانی که ورزش میکنند، نصف افرادی است که ورزش منظم ندارند. به بیان دیگر، ریسک داشتن اضافه وزن در بین کسانی که ورزش منظم ندارند، تقریبا 1.57 () برابر کسانی است که ورزش منظم دارند.
نکته: زمانی که ریسک نسبی، کمتر از ۱ باشد، میتوان مزیت نسبی (Relative Benefit) یا به اختصار را هم به صورت زیر بدست آورد.
رابطه ۲
به این ترتیب مطابق با مثال ۳، میتوان گفت که اضافه وزن در نزد کسانی که ورزش منظم میکنند، طبق رابطه ۲، به میزان ۴۳٪ کمتر از کسانی است که بطور نامنظم ورزش میکنند.

تفسیرهای نادرست از ریسک نسبی
گاهی بعضی از محققین، ریسک نسبی را با «نسبت بخت» (Odds Ratio) یا «ریسک مطلق» (Absolute Risk) اشتباه میگیرند. در ادامه متن، این دو شاخص را با ریسک نسبی مقایسه خواهیم کرد.
مقایسه ریسک نسبی و نسبت بخت
همانطور که گفته شد، ریسک نسبی، نسبت احتمال رخداد یک پیشامد در حضور یا عدم رخداد یک عامل است. در نتیجه از آن به عنوان یک احتمال شرطی (Conditional Probability) استفاده میکنند. در حالیکه نسبت بختها چنین نیست. نحوه محاسبه نسبت بختها برای پیشامد را در زیر میبینید.
رابطه ۳
کاملا مشخص است که نسبت بختها (در رابطه ۳) با ریسک نسبی براساس احتمال شرطی و طبق رابطه ۱ تفاوت دارد.
مقایسه ریسک نسبی و ریسک مطلق
«ریسک مطلق» (Absolute Risk)، دقیقاً نشان دهنده ریسک است. به این ترتیب میتوان آن را براساس احتمال رخداد یک پیشامد برای اساس یک تیمار یا عامل مشخص کرد. برای مثال، اگر یک نفر از ۱۰ نفر، که در آزمایشگاه بیمارستان کار میکنند، مبتلا به عفونت چشمی باشد، ریسک ابتلا به این بیماری در این گروه ۱۰ درصد است به این معنی که از هر ۱۰۰ نفر کارکنان آزمایشگاه بیمارستانها، ۱۰ نفر دچار عفونت چشمی میشوند. در مقابل افرادی که به آزمایشگاه بیمارستان رفت و آمد ندارند، با احتمال یک درصد، دچار عفونت چشم هستند. در نتیجه ریسک (ریسک مطلق) ابتلا به عفونت چشم در بین این گروه فقط یک درصد است.
حال اگر نسبت این دو ریسک را بدست آوریم، مشخص میشود که ابتلا به عفونت چشمی در بین کارکنان آزمایشگاهی بیمارستان، ۱۰ برابر دیگر کارکنان است و شیوع این عفونت در این گروه بسیار زیاد است.
همانطور که مشاهده میکنید، مقادیر کوچک (یک درصد از کارکنان بیمارستان مبتلا به عفونت چشمی) باعث تغییرات زیاد در ریسک نسبی میشود در حالیکه ریسک مطلق تغییرات زیادی نخواهد داشت.
از طرفی ممکن است مخرج کسر مربوط به ریسک نسبی بسیار کوچک بوده بطوری که ریسک نسبی نتواند میزان صحیحی برای تاثیرگذاری عامل را نشان دهد و به اصطلاح بزرگنمایی صورت گیرد. برعکس زمانی که مخرج کسر ریسک نسبی، بسیار بزرگ باشد، باز هم اثر گذاری عامل کوچکنمایی میشود.
بنابراین هنگام ارائه گزارشات آماری بهتر است هم ریسک مطلق و هم ریسک نسبی گزارش شوند تا با چنین مسائلی روبرو نشویم.
محاسبه ریسک نسبی در جدول توافقی
همانطور که در قسمتهای قبلی خواندید، ریسک نسبی از تقسیم ریسک مطلق در زمانی که یک عامل به کار گرفته شده و بدون حضور آن عامل، حاصل میشود. در این قسمت به کمک محاسباتی که براساس یک «جدول توافقی» (Contingency Table) انجام میدهیم، شیوه بدست آوردن ریسک نسبی را اجرا خواهیم کرد.
جدول توافقی ۲×۲ زیر را در نظر بگیرید که مربوط به دو گروه آزمون (Intervention) و کنترل (Control) است. رخداد یک پیشامد (Event) و عدم آن (Non-Event) نیز در جدول گنجانده شده است.
| حضور یا عدم حضور عامل (Group) | ||
| عامل-Intervention یا (I) | کنترل-Control یا (C) | |
| رخداد پیشامد- Event یا (E) | IE | CE |
| بدون رخداد پیشامد- Non events یا (N) | IN | CN |
اگر گروه آزمون را با و گروه کنترل را با ، همچنین رخداد پیشامد را با و متمم آن یا عدم رخداد چنین پیشامدی را با مشخص کنیم، محاسبه ریسک نسبی براساس فرمول زیر صورت خواهد گرفت.
رابطه ۴
توزیع نمونهای لگاریتم تقریبا نرمال با انحراف معیار زیر است:
در نتیجه یک فاصله اطمینان برای به شکل زیر محاسبه میشود.
که در آن مقدار نمره استاندارد در سطح معنیداری است.
توجه دارید که فاصله اطمینان ارائه شده مربوط به لگاریتم ریسک نسبی است و برای بدست آوردن فاصله اطمینان باید کرانها را به صورت نمایی در نظر بگیرید.
نکته: با توجه به علامتهایی که در جدول بالا ارائه شد، نسبت بختها (Odds Ratio) نیز به شکل زیر بدست میآید.
حال اگر بسیار کوچکتر از و نیز از بسیار کمتر باشد، آنگاه میتوان به صورت تقریبی نوشت:
و
که در این صورت ریسک نسبی تقریبا با نسبت بختها برابر خواهد شد.
محاسبه ریسک نسبی با دیدگاه بیزی
همانطور که در قسمتهای قبلی توضیح داده شد، ریسک نسبی را به صورت یک احتمال شرطی و مطابق با رابطه ۱، میتوان نمایش داد.
در اینجا برای نشان دادن هر یک از احتمالهای شرطی گفته شده، از «قضیه بیز» (Bayes Theorem) استفاده میکنیم.
با استفاده از قضیه بیز و ساده کردن بعضی از جملهها، به رابطه زیر خواهیم رسید.
رابطه ۵
به این ترتیب، ریسک نسبی را به صورت محاسبه براساس قضیه بیز و مطابق با رابطه ۵ میتوان نوشت. واضح است که در این بین، «نسبت پسین» (Posterior Ratio) برای مشاهداتی که تحت عامل قرار گرفتهاند در نظر گرفته شده است. در نتیجه اگر نسبت پسین تقریا برابر با «نسبت پیشین» (Prior Ratio) باشد، اثر عامل تقریبا برابر با یک است که مثلا نشانگر بی اثر بودن سیگار روی داشتن سرطان ریه است. زیرا سیگاری بودن نتوانسته است تغییری روی نرخ سرطان ریه داشته باشد.
از طرف دیگر اگر نسبت پسین، کوچکتر یا بزرگتر از نسبت پیشین باشد، آنگاه بیماری در اثر متغیر عامل تحت تاثیر قرار داشته و میزان این تغییرات همان ریسک نسبی خواهد بود.
بررسی کاهش و افزایش ریسک نسبی
تغییراتی که ریسک در مداخله یک عامل در بردارد، ممکمن است به صورت «کاهش ریسک نسبی» (Relative Risk Reduction) مشخص میشود. به این ترتیب وجود یا حضور یک عامل مداخلهگر، میتواند باعث تغییر در مقدار ریسک نسبی شود. به منظور بررسی این موضوع و آشنایی با نحوه محاسبات آن، به یک مثال میپردازیم.
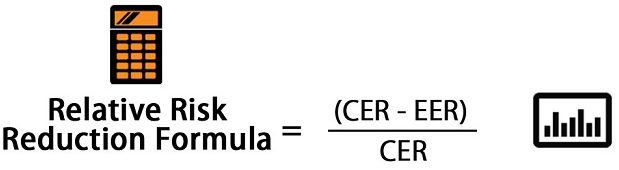
مثال ۴: جدول اطلاعاتی زیر را در نظر بگیرید. فرض شده است که نمایانگر تعداد در گروه آزمایش (Experimental Group) و نیز مربوط به گروه کنترل (Control Group) است. همچنین هم بیانگر رخداد (Event) و هم عدم رخداد (Non-event) است. همچنین تمام مشاهدات (Total Subject) و در انتها نیز نرخ رخداد (Event Rate) است.
| مثال از کاهش ریسک | |||
| گروه آزمایش (E) | گروه کنترل (C) | جمع کل | |
| رخداد (E) | EE = 15 | CE = 100 | 115 |
| عدم رخداد (N) | EN = 135 | CN = 150 | 285 |
| کل مشاهدات (S) | ES = EE + EN = 150 | CS = CE + CN = 250 | 400 |
| نرخ رخداد (ER) | EER = EE /ES = 0.1 | CER = CE / CS = 0.4 | |
به این ترتیب میزان کاهش ریسک و پارامترهای دیگر آن مطابق با جدول زیر قابل محاسبهاند.
| معادله | شاخص توصیفی | مخفف | مقدار |
| CER-EER | کاهش ریسک مطلق (Absolute Risk Reduction) | ARR | 0.3 |
| (CER - EER) / CER | کاهش ریسک نسبی (Relative Risk Reduction) | RRR | 0.75 |
| 1 / (CER − EER) | تعداد مشاهدات مورد احتیاج برای تیمار | NNT | 3.33 |
| EER / CER | ریسک نسبی (Risk Ratio- Relative Risk) | RR | 0.25 |
| (EE / EN) / (CE / CN) | نسبت بخت (Odds Ratio) | OR | 0.167 |
همین جدول نیز میتواند مبنای محاسبه افزایش ریسک باشد. این امر زمانی رخ میدهد که CER-EER، منفی باشد. به جداولی که در ادامه آمدهاند، توجه کنید تا شیوه محاسبه آن را هم ببینید.
| مثال از افزایش ریسک | |||
| گروه آزمایش (E) | گروه کنترل (C) | جمع کل | |
| رخداد (E) | EE = 75 | CE = 100 | 115 |
| عدم رخداد (N) | EN = 75 | CN = 150 | 285 |
| کل مشاهدات (S) | ES = EE + EN = 150 | CS = CE + CN = 250 | 400 |
| نرخ رخداد (ER) | EER = EE /ES =0.5 | CER = CE / CS = 0.4 | |
به این ترتیب میزان افزایش ریسک و پارامترهای دیگر آن مطابق با جدول زیر قابل محاسبهاند.
| معادله | شاخص توصیفی | مخفف | مقدار |
| EER-CER | افزایش ریسک مطلق (Absolute Risk Increase) | ARI | 0.1 |
| (EER - CER) / CER | افزایش ریسک نسبی (Relative Risk Increase) | RRI | 0.25 |
| 1 / (EER − CER) | تعداد مشاهدات مورد احتیاج برای عدم تیمار | NNH | 10 |
| EER / CER | ریسک نسبی (Risk Ratio- Relative Risk) | RR | 1.25 |
| (EE / EN) / (CE / CN) | نسبت بخت (Odds Ratio) | OR | 1.5 |
ریسک نسبی و کاربردهای آن در مدل جمعی و رگرسیون پواسن
اغلب از نسبت بختها به عنوان ملاک مطالعات و مقایسههای «مورد-شاهدی» (Case-Control Study) استفاده میشود به طوری که محاسبه نسبت ریسک امکانپذیر نباشد. برای مثال در «رگرسیون لجستیک» (Logistic Regression)، برای نشان دادن اهمیت یا کارایی مدل از نسبت لگاریتم بخت به جای ریسک نسبی استفاده میشود. بطوری که لگاریتم نسبت بختها را میتوان به صورت یک رابطه خطی (Linear Form) با «متغیرهای توصیفی» (Explanatory Variables) نشان داد.
فرض کنید که نسبت بختها برای بهبودی یک بیماری در اثر مصرف یک دارو خاص، بین گروه بیماران هفتاد ساله و گروه بیماران ۶۰ ساله محاسبه شده است. این مقدار درست شبیه یک مدل رگرسیون لجستیک، نشان دهنده میزان عملکرد دارو و مقایسه آن در بین این دو گروه است. در حالیکه ریسک نسبی ممکن است کاملا با خروجی رگرسیون لجستیک متفاوت باشد.
ولی در عوض زمانی که از مدلهای رگرسیونی با توزیع خاص (مثل توزیع پواسن) استفاده میشود، بهتر است نسبت ریسک برای نشان دادن اثر متغیرهای توصیفی روی متغیر وابسته استفاده کرد. برای مثال فرض کنید که عمل A دارای ریسک 99.9 درصدی است در حالیکه عمل B ریسک ۹۰ درصدی دارد. در این صورت، ریسک نسبی تقریبا برابر با ۱ است. ولی با توجه به عمل A، بخت رخداد آن تقریبا ۱۰ برابر رخداد B است.
درمدلهای آماری، مانند «رگرسیون پواسون» (Poisson Regression) که برحسب تعداد پیشامدهای در هر واحد از یک رخداد به کار میروند، ریسک نسبی، توصیف بهتری از تاثیر متغیرهای توصیفی روی متغیر وابسته که به صورت نرخ یا تعداد رخدادها در یک واحد مشخص است، ارائه میدهند. در حالیکه مثلا در گرسیون لجستیک باینری، با توجه به دو مقداری بودن متغیر وابسته، نسبت بختها بیانگر بهتری از تاثیر گذاری متغیرهای توصیفی خواهد داشت.
خلاصه و جمعبندی
در این نوشتار با مفهوم ریسک نسبی (Relative Risk) در مدل آماری (Statistical models) با دو وضعیت و دو شیوه محاسباتی یعنی به کمک جدول توافقی و همچنین روش بیزی مشابه با قضیه بیز (Bayes Theorem)، آشنا شدیم. نتایج حاصل از این شاخص، اثر گذاری متغیرهای یک مدل را روی متغیر پاسخ نشان میدهد.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای آمار و احتمالات
- آموزش آماده سازی داده ها برای تحلیل آماری در SPSS
- مجموعه آموزشهای SPSS
- آموزش نرم افزار آماری SPSS
- ضریب تغییرات در SPSS — راهنمای کاربردی
- معیار ارزیابی AIC در مدل های احتمالی — از صفر تا صد
- معیار ارزیابی BIC در مدل های احتمالی — از صفر تا صد
^^












