دمای آدیاباتیک شعله – به زبان ساده

پیش از این در مجله فرادرس، فرآیند آدیاباتیک و معادلات مربوط به انرژی را در آن بررسی کردیم. در این مقاله به مفهوم دمای آدیاباتیک شعله (Adiabatic Flame Temperature) خواهیم پرداخت. محفظه احتراق شکل زیر را در نظر بگیرید. اگر هیچگونه کاری انجام نشود و تغییری هم در انرژیهای جنبشی و پتانسیل رخ ندهد، انرژی شیمیایی آزاد شده در فرآیند احتراق دو راه در پیش رو دارد. یا باید به عنوان گرما در محیط آزاد شود؛ یا از آن برای بالا بردن دمای محصولات احتراق استفاده شود.
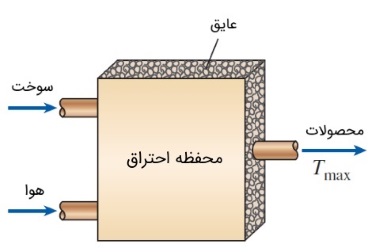
هرچه افت حرارتی کمتر باشد، افزایش دما بیشتر خواهد بود. در یک حالت حدی که هیچ مقداری از گرما در محیط آزاد نمیشود ($$\large Q\: =\:0$$)، دمای محصولات احتراق به ماکسیمم مقدار خود خواهند رسید. این دما، به دمای شعله یا دمای احتراق آدیاباتیک (Adiabatic Combustion Temperature) معروف است. برای تعیین دمای آدیاباتیک شعله در یک فرآیند احتراق جریان پایدار، کافی است $$\large Q \:=\: 0$$ و $$\large W \:=\: 0$$ را اعمال کنیم.
$$\large Q \:-\: W \:=\: H_{prod} \:-\: H_{react} \\~\\
\large H_{prod} \:=\: H_{react} \\~\\
\large \sum_{}^{} N_p (\overline{h}^ \circ _f \:+\: \overline{h} \:-\: \overline{h}^ \circ)_p \:=\: \sum_{}^{} N_r (\overline{h}^ \circ _f \:+\: \overline{h} \:-\: \overline{h}^ \circ)_r$$
آنتالپی واکنش در حالت مرجع استاندارد را با $$\large \overline{h}^ \circ _f$$ نشان دادهایم. $$\large \overline{h}$$ و $$\large \overline{h}^ \circ$$ نیز به ترتیب، آنتالپی محسوس در حالت فعلی و آنتالپی محسوس در حالت مرجع استاندارد ($$\large 25 \:^\circ C$$ و $$\large 1\: \text{atm}$$) است. هنگامی که واکنشدهندهها و حالت آن مشخص باشد، آنتالپی واکنشدهندهها ($$\large H_{react}$$) به راحتی تعیین میشود. اما محاسبه آنتالپی محصولات یا فرآوردهها ($$\large H_{prod}$$) به این سادگی نیست. زیرا قبل از انجام واکنش، دمای محصولات را نمیتوان اندازهگیری کرد.
چگونگی محاسبه دمای آدیاباتیک شعله
بنابراین، برای تعیین دمای آدیاباتیک شعله باید از روش تکرار شونده (Iterative Technique) استفاده کنیم. مگر اینکه معادلات تغییر آنتالپی محصولات احتراق مشخص باشد. ابتدا دمایی برای گازهای محصول فرض میکنیم و $$\large H_{prod}$$ براساس این دمای فرضی تعیین میشود. اگر آنتالپی در این دمای فرضی با $$\large H_{react}$$ برابر نباشد، محاسبات با یک دمای دیگر تکرار میشود. سپس میتوانیم با درونیابی این دو عدد به دست آمده، دمای آدیاباتیک شعله را مشخص کنیم. اگر از هوا به عنوان عامل اکسیداسیون استفاده شود، بخش زیادی از محصولات گازی شامل $$\large N_2$$ خواهد بود. در چنین حالتی برای حدس اول در مورد دمای آدیاباتیک شعله بهتر است تمام محصولات را گاز $$\large N_2$$ فرض کنیم.
در محفظههای احتراق، ملاحظات متالوژیکی، ماکسیمم دمایی را که هر ماده میتواند تحمل کند، با محدودیت مواجه میسازد. از این رو، دمای آدیاباتیک شعله یکی از مهمترین مواردی است که باید در حین طراحی محفظههای احتراق، توربینهای گازی و نازلها در نظر گرفته شود. ماکسیمم دمایی که در این تجهیزات اتفاق میافتد، به اندازه قابل توجهی نسبت به دمای آدیاباتیک شعله پایینتر است. زیرا معمولاً در بسیاری از فرآیندهای احتراق، احتراق به صورت کامل انجام نمیشود، اتلاف حرارت اتفاق میافتد و همچنین برخی از گازهای حاصل از احتراق، در دماهای بالا تجزیه میشوند. با تنظیم حجم هوای اضافی که در نقش خنککننده ظاهر میشود، میتوان ماکسیمم دما درون محفظه احتراق را کنترل کرد.
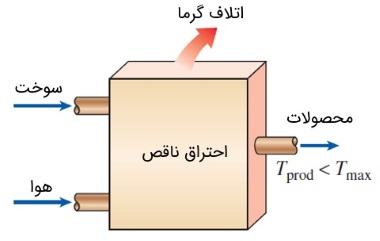
توجه کنید که دمای آدیاباتیک شعله یک سوخت، منحصر به فرد نیست و به سه عامل مختلف بستگی دارد:
- حالت فیزیکی واکنش دهندهها
- میزان واکنش دهنده محدود کننده و واکنش دهنده اضافی
- حجم هوای نظری
مثال: دمای آدیاباتیک شعله در احتراق یکنواخت
سؤال: اوکتان مایع با فرمول شیمیایی $$\large C_8H_{18}$$ به طور یکنواخت وارد محفظه احتراق یک توربین گاز میشود. دما و فشار اوکتان به ترتیب برابر $$\large 25 \:^\circ C$$ و $$\large 1 \:atm$$ است و به همراه هوا میسوزد. هوا هم با همین شرایط وارد محفظه احتراق میشود. با توجه به شکل زیر، دمای آدیاباتیک شعله را در موارد زیر به دست آورید.
الف) احتراق کامل با $$\large 100$$ درصد هوای نظری
ب) احتراق کامل با $$\large 400$$ درصد هوای نظری
پ) احتراق ناقص با $$\large 90$$ درصد هوای نظری و وجود $$\large \text {CO}$$ در محصولات
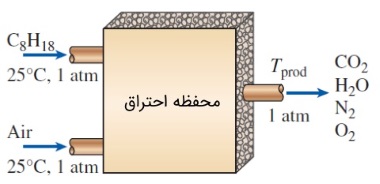
پاسخ: الف) معادله موازنه شده برای فرآیند احتراق با حجم هوای نظری به صورت زیر است.
$$\large \text{C}_8 \text{H}_{18} \:+\: 12.5 (\text{O}_2 \:+\: 3.76 \: \text{N} _2) \:\rightarrow\: 8\: \text{CO}_2 \:+\: 9\: \text{H}_2 \text{O} \:+\: 47\: \text{N}_2$$
برای نوشتن رابطه دمای آدیاباتیک شعله ($$\large H_{prod} \:=\: H_{react}$$) در این مورد به طریق زیر عمل میکنیم. زیرا تمام واکنش دهندهها در حالت مرجع استاندارد قرار دارند و برای $$\large O_2$$ و $$\large N_2$$، رابطه $$\large \overline{h}^ \circ _f \:=\:0$$ برقرار است.
$$\large \sum_{}^{} N_p (\overline{h}^ \circ _f \:+\: \overline{h} \:-\: \overline{h}^ \circ)_p \:=\: \sum_{}^{} N_r \overline{h}^ \circ _{f,r} \:=\: (N\overline{h}^ \circ _f)_{C_8H_{18}}$$
جدول زیر، مقادیر $$\large \overline{h}^ \circ _f$$ و $$\large h$$ مربوط به مادههای مختلف را در دمای $$\large 298 \:K$$ نشان میدهد.
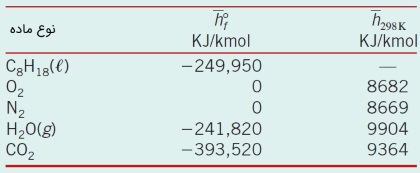
مقادیر جدول را در رابطه اخیر جایگذاری میکنیم.
$$\large (8 \:kmol \text{C} \text{O}_2) [(-\: 393,520 \:+\: \overline{h}_{\text{C} \text{O}_2} \:-\: 9,364) \:kJ/ kmol\: \text{C} \text{O}_2] \\~\\
\large \:+\: (9 \:kmol \text{H}_2 \text{O}) [(-\: 241,820 \:+\: \overline{h}_{\text{H}_2 \text{O}} \:-\: 9,904) \:kJ/ kmol\: \text{H}_2 \text{O}] \\~\\
\large \:+\: (47 \:kmol \text{N}_2) [( 0 \:+\: \overline{h}_{\text{N}_2} \:-\: 8,669) \:kJ/ kmol\: \text{N}_2] \\~\\
\large \:=\: (1\: kmol \text{C}_8 \text{H}_{18}) (-\: 249,950 \:kJ/kmol \:\text{C}_8 \text{H}_{18}) \\~\\
\large \Rightarrow ~~~ 8\overline{h}_{\text{C} \text{O}_2} \:+\: 9\overline{h}_{\text{H}_2 \text{O}} \:+\: 47\overline{h}_{\text{N}_2} \:=\: 5,656,081 \:kJ$$
شاید اینگونه به نظر برسد که در حال حاضر یک معادله با سه مجهول در اختیار داریم. ولی در واقع، تنها مجهول ما دمای محصولات ($$\large T_{prod}$$) است. زیرا در گازهای ایدهآل، آنتالپی فقط به دما بستگی دارد. بنابراین برای حل این معادله و تعیین دمای آدیاباتیک شعله میتوانیم از EES یا روش سعی و خطا استفاده کنیم. برای اولین حدس، سمت راست رابطه بالا را به تعداد کل مولها تقسیم میکنیم.
$$\large 5,646,081/ (8\:+ \:9\: +\:47) \:=\: 88,220 \:~ kJ/kmol$$
این مقدار آنتالپی، با دمای $$\large 2650 \:K$$ برای $$\large \text{ N}_2$$، دمای $$\large 2100 \:K$$ برای $$\large \text{ H}_2 \text{O}$$ و دمای $$\large 1800 \:K$$ برای $$\large \text{C} \text{O}_2$$ متناظر است. با توجه به اینکه بیشتر مولها، $$\large \text{N}_2$$ هستند، $$\large T_{prod}$$ باید به عدد دمای $$\large 2650 \:K$$ نزدیک و از آن، کمتر باشد. از این رو، دمای $$\large 2400 \:K$$ را برای حدس اولیه در مورد دمای آدیاباتیک شعله انتخاب میکنیم. آنتالپی این سه ماده در دمای $$\large 2400 \:K$$ را میتوانیم با مراجعه به جداول ترمودینامیکی بیابیم.
$$\large 8\overline{h}_{\text{C} \text{O}_2} \:+\: 9\overline{h}_{\text{H}_2 \text{O}} \:+\: 47\overline{h}_{\text{N}_2} \:=\: 8\: \times \:125,152 \\~\\
\large \:+\: 9\: \times \:103,508 \:+\: 47\: \times \:79,320 \:=\: 5,660,828 \:kJ$$
این مقدار، کمی از $$\large 5,646,081 \:kJ$$ بیشتر است. بنابراین، دما باید اندکی پایینتر از $$\large 2400 \:K$$ باشد. به همین دلیل، دمای $$\large 2350 \:K$$ را برای حدس دوم انتخاب میکنیم. در این دما، آنتالپی به صورت زیر محاسبه میشود.
$$\large 8\:\times \:122,091 \:+\: 9\:\times \:100,846 \:+\: 47\: \times \:77,496 \:=\: 5,526,654 \:~ kJ$$
همانطور که میبینید، این مقدار از $$\large 5,646,081 \:kJ$$ بیشتر است. در نتیجه، دما عددی بین $$\large 2350 \:K$$ و $$\large 2400 \:K$$ خواهد بود. با به کارگیری روش درونیابی، دمای مورد نظر برابر با $$\large T_{prod} \:=\: 2395 \:K$$ به دست میآید.
ب) معادله موازنه شده برای احتراق کامل با $$\large 400$$ درصد هوای نظری به این صورت است:
$$\large \text{C}_8 \text{H}_{18} \:+\: 50 (\text{O}_2 \:+\: 3.76 \: \text{N} _2) \:\rightarrow\: 8\: \text{CO}_2 \:+\: 9\: \text{H}_2 \text{O} \:+\: 37.5\: \text{O}_2 \:+\: 188\: \text{N}_2$$
با روشی مشابه با آنچه در قسمت الف به جواب رسیدیم، دمای آدیاباتیک شعله در این حالت، برابر با $$\large T_{prod} \:=\: 962 \:K$$ به دست میآید. همانطور که مشاهده میکنید، به دلیل زیاد بودن حجم هوای نظری، دمای محصولات به اندازه قابل توجهی کاهش یافته است.
پ) معادله موازنه شده برای فرآیند احتراق ناقص با $$\large 90$$ درصد هوای نظری به شکل زیر نوشته میشود.
$$\large \text{C}_8 \text{H}_{18} \:+\: 11.25 (\text{O}_2 \:+\: 3.76 \: \text{N} _2) \:\rightarrow\: 5.5\: \text{CO}_2 \:+\: 9\: \text{H}_2 \text{O} \:+\: 2.5\: \text{C} \text{O} \:+\: 42.3\: \text{N}_2$$
با تکرار روشی که در قسمتهای قبل از آن استفاده کردیم، به پاسخ $$\large 2236 \:K$$ میرسیم. همانطور که ملاحظه کردید، بیشترین دمای آدیاباتیک شعله هنگامی اتفاق میافتد که احتراق کامل با حجم هوای نظری $$\large 100$$ درصد داشته باشیم.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- ترمودینامیک — از صفر تا صد
- فرآیند آدیاباتیک — به زبان ساده
- فرآیند احتراق یا سوختن — از صفر تا صد
- تعریف گرما و دما در ترمودینامیک — به زبان ساده
^^










خیلی ممنون. ساده و قابل فهم بود