تحلیل حالت دائمی سینوسی — به زبان ساده (+ دانلود فیلم آموزش رایگان)

تحلیل حالت دائمی سینوسی یکی از روش‌های بسیار مهم در تجزیه و تحلیل مدارت الکتریکی AC است. در مطالب قبلی مجله فرادرس با روش به دست آوردن پاسخ حالت دائمی (Steady State Response) برای ورودی‌های سینوسی، با استفاده از فازورها (Phasor) آشنا شدیم. همچنین می‌دانیم که قوانین اهم (Ohm) و کیرشهف (Kirchhoff) در مدارات AC نیز قابل اعمال هستند. روش‌های تحلیل مش و تحلیل گره نیز در مدارات DC قبلا توضیح داده شده‌اند. در این مطلب قصد داریم به بررسی تحلیل حالت دائمی سینوسی و نحوه اعمال روش‌های تحلیل مش و تحلیل گره در مدارات AC بپردازیم.

تحلیل مدارات AC همیشه در سه گام اساسی انجام می‌گیرد:

1. ابتدا باید مدار به حوزه فرکانسی یا فازوری انتقال داده شود.
2. مسئله با استفاده از تکنیک‌های مداری مانند تحلیل مش و تحلیل گره و یا جمع آثار حل شود.
3. جواب‌های به دست آمده در حوزه فرکانسی به حوزه زمان منتقل شوند.

توجه کنید که اگر مسئله خود در حوزه زمان مطرح شده باشد، از گام اول صرف نظر می‌شود. در گام دوم تحلیل مدار دقیقا مانند آن‌چه در مدارات DC انجام می‌گرفت، تکرار می‌شود و تنها تفاوت در وجود اعداد مختلط در محاسبات حوزه فرکانس است. حال به بررسی روش تحلیل گره در تحلیل حالت دائمی سینوسی می‌پردازیم.

آنالیز گره در تحلیل حالت دائمی سینوسی

اساس روش آنالیز گره بر قانون جریان کیرشهف استوار است. از آن‌جا که قانون KCL در مورد فازورها هم قابل اعمال است، در نتیجه می‌توان برای تحلیل مدارات AC از روش تحلیل گره استفاده کرد. در مثال زیر به بررسی نحوه اعمال این روش می‌پردازیم.

فیلم آموزش مبانی مهندسی برق ۱ در فرادرس

کلیک کنید

مثال ۱

در مدار زیر $$i_x$$ را با استفاده از روش تحلیل گره بیابید.

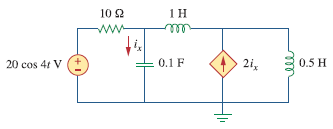
حل: ابتدا مدار را به حوزه فرکانس منتقل می‌کنیم.

$$\begin{aligned} 20 \cos 4 t & \Rightarrow \quad 20 / 0^{\circ}, \quad \omega=4 \mathrm{rad} / \mathrm{s} \\ 1 \mathrm{H} & \Rightarrow \quad j \omega L=j 4 \\ 0.5 \mathrm{H} & \Rightarrow \quad j \omega L=j 2 \\ 0.1 \mathrm{F} & \Rightarrow \frac{1}{j \omega C}=-j 2.5 \end{aligned}$$

بنابراین مدار معادل فرکانسی به صورت زیر خواهد بود.

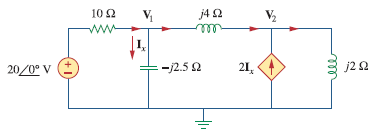
حال در گره ۱ KCL اعمال می‌کنیم.

$$\frac{20-\mathbf{V}_{1}}{10}=\frac{\mathbf{V}_{1}}{-j 2.5}+\frac{\mathbf{V}_{1}-\mathbf{V}_{2}}{j 4}$$

معادله بالا را بازنویسی می‌کنیم.

$$(1+j 1.5) \mathbf{V}_{1}+j 2.5 \mathbf{V}_{2}=20$$

با اعمال KCL در گره شماره ۲ داریم:

$$2 \mathbf{I}_{x}+\frac{\mathbf{V}_{1}-\mathbf{V}_{2}}{j 4}=\frac{\mathbf{V}_{2}}{j 2}$$

از طریق جایگذاری $$\mathbf{I}_{x}=\mathbf{V}_{1} /-j 2.5$$ در معادله بالا داریم:

$$\frac{2 \mathbf{V}_{1}}{-j 2.5}+\frac{\mathbf{V}_{1}-\mathbf{V}_{2}}{j 4}=\frac{\mathbf{V}_{2}}{j 2}$$

پس از ساده کردن معادله بالا داریم:

$$11 \mathbf{V}_{1}+15 \mathbf{V}_{2}=0$$

معادلات بالا را می‌توان به فرم ماتریسی نیز نوشت.

$$\left[\begin{array}{cc}{1+j 1.5} & {j 2.5} \\ {11} & {15}\end{array}\right]\left[\begin{array}{l}{\mathbf{V}_{1}} \\ {\mathbf{V}_{2}}\end{array}\right]=\left[\begin{array}{c}{20} \\ {0}\end{array}\right]$$

حال باید دترمینان ماتریس‌ را به دست بیاوریم.

$$\Delta=\left|\begin{array}{cc}{1+j 1.5} & {j 2.5} \\ {11} & {15}\end{array}\right|=15-j 5$$

دستگاه معادلات بالا را می‌توان به روش کرامر حل کرد.

$$\Delta_{1}=\left|\begin{array}{cc}{20} & {j 2.5} \\ {0} & {15}\end{array}\right|=300, \quad \Delta_{2}=\left|\begin{array}{cc}{1+j 1.5} & {20} \\ {11} & {0}\end{array}\right|=-220$$

$$\begin{array}{l}{\mathbf{V}_{1}=\frac{\Delta_{1}}{\Delta}=\frac{300}{15-j 5}=18.97 / 18.43^{\circ} \mathrm{V}} \\ {\mathbf{V}_{2}=\frac{\Delta_{2}}{\Delta}=\frac{-220}{15-j 5}=13.91 / 198.3^{\circ} \mathrm{V}}\end{array}$$

در نتیجه جریان $$I_x$$ را می‌توان به صورت زیر به دست آورد:

$$\mathbf{I}_{x}=\frac{\mathbf{V}_{1}}{-j 2.5}=\frac{18.97 / 18.43^{\circ}}{2.5 \angle-90^{\circ}}=7.59 / 108.4^{\circ} \mathrm{A}$$

در نهایت باید جواب به دست آمده را به حوزه زمان منتقل کنیم.

$$i_{x}=7.59 \cos \left(4 t+108.4^{\circ}\right) \mathrm{A}$$

آنالیز مش در تحلیل حالت دائمی سینوسی

قانون ولتاژ کیرشهوف پایه و اساس روش تحلیل مش را شکل می‌دهد. این روش را می‌توان در مدارات AC نیز به کار برد. توجه کنید که روش تحلیل مش را باید در مدارات مسطح دو وجهی (Planar) به کار برد. حال نحوه اعمال این روش را در مثال زیر بررسی می‌کنیم.

فیلم آموزش تحلیل حالت دائمی سینوسی (رایگان) در فرادرس

کلیک کنید

مثال ۲

جریان $$I_o$$ را در مدار شکل زیر از طریق روش تحلیل مش به دست آورید.

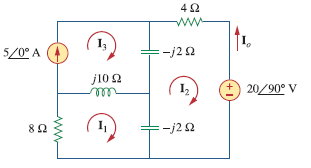
حل: قانون KVL را در مش ۱ اعمال می‌کنیم.

$$(8+j 10-j 2) \mathbf{I}_{1}-(-j 2) \mathbf{I}_{2}-j 10 \mathbf{I}_{3}=0$$

در مش شمار ۲ نیز قانون KVL را اعمال می‌کنیم.

$$\left(4-j 2-j 2 \mathrm{I}_{2}-(-j 2) \mathrm{I}_{1}-(-j 2) \mathrm{I}_{3}+20 / 90^{\circ}=0\right.$$

جریان $$I_3$$ در مش شماره ۳ برابر با ۵ آمپر است. این مقدار را در معادلات بالا جایگذاری می‌کنیم.

$$\begin{aligned}(8+j 8) \mathbf{I}_{1}+j 2 \mathbf{I}_{2} &=j 50 \\ j 2 \mathbf{I}_{1}+(4-j 4) \mathbf{I}_{2} &=-j 20-j 10 \end{aligned}$$

این معادلات را می‌توانیم به فرم ماتریسی بازنویسی کنیم.

$$\left[\begin{array}{cc}{8+j 8} & {j 2} \\ {j 2} & {4-j 4}\end{array}\right]\left[\begin{array}{l}{\mathbf{I}_{1}} \\ {\mathbf{I}_{2}}\end{array}\right]=\left[\begin{array}{c}{j 50} \\ {-j 30}\end{array}\right]$$

حال مانند مثال قبل دترمینان ماتریس را به دست می‌آوریم.

$$\Delta=\left|\begin{array}{cc}{8+j 8} & {j 2} \\ {j 2} & {4-j 4}\end{array}\right|=32(1+j)(1-j)+4=68$$

دستگاه معادلات را به روش کرامر حل می‌کنیم.

$$\begin{aligned} \Delta_{2}=\left|\begin{array}{cc}{8+j 8} & {j 50} \\ {j 2} & {-j 30}\end{array}\right|=340-j 240=416.17 \angle-35.22^{\circ} \end{aligned}$$

$$\begin{aligned}\mathbf{I}_{2}=\frac{\Delta_{2}}{\Delta}=& \frac{416.17 /-35.22^{\circ}}{68}=6.12 /-35.22^{\circ} \mathrm{A} \end{aligned}$$

حال جریان $$I_o$$ را می‌توان به صورت زیر به دست آورد.

$$\mathbf{I}_{o}=-\mathbf{I}_{2}=6.12 / 144.78^{\circ} \mathrm{A}$$

اگر مطالب بیان شده برای شما مفید بوده و می‌خواهید درباره موضوعات مرتبط با آن بیشتر بدانید، پیشنهاد می‌کنیم به آموزش‌های زیر مراجعه کنید:

• مجموعه آموزش‌های مهندسی برق
• آموزش مدارهای الکتریکی ۱
• مجموعه آموزش‌ مهندسی الکترونیک
• آموزش مدارهای الکتریکی ۱ (مرور و حل تست)
• قضیه هم پاسخی — به زبان ساده
• قضیه نورتن (Nortons Theorem) — مفاهیم اصلی
• قضیه تونن (Thevenin’s Theorem) — مفاهیم کلیدی

^^