قضیه هم پاسخی — به زبان ساده(+ دانلود فیلم آموزش رایگان)
قضیه هم پاسخی (Reciprocity Theorem) در مدارهای الکتریکی با تنها یک منبع ولتاژ یا جریان مستقل مطرح میشود. این قضیه برای منابع وابسته ولتاژ و جریان قابل استفاده نیست، اما هم به منابع ولتاژ مستقل و هم به منابع جریان مستقل قابل اعمال است. در این نوشته سعی میکنیم این قضیه را برای هر دو حالت بررسی کرده و از هر کدام یک نمونه مثال ارائه کنیم.
قضیه هم پاسخی برای منابع ولتاژ مستقل
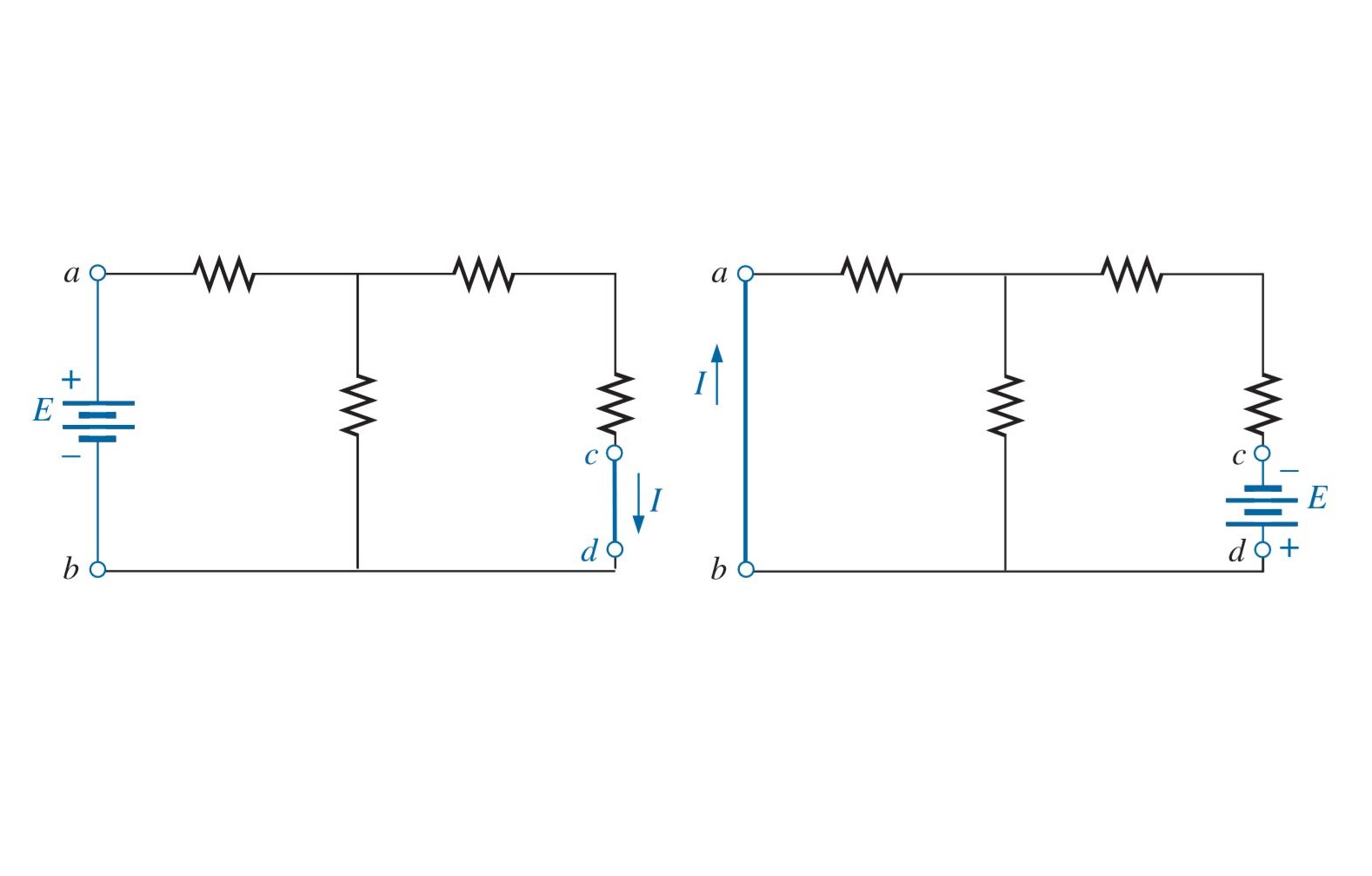
فرض کنید منبع ولتاژ مستقل یک مدار الکتریکی در شاخه nام آن جریان الکتریکی $$I$$ را تولید کند (منظور از شاخه یک مسیر برای عبور جریان الکتریکی است). حال اگر محل منبع ولتاژ مستقل را تغییر دهیم به صورتی که از محل اولیه برداشته شده و به شاخه nام منتقل شود، آنگاه منبع ولتاژ مستقل (در محل جدید) در محل قبلی خود جریانی تولید میکند.
این جریان برابر با جریان شاخه nام ناشی از منبع ولتاژ مستقل در محل قبلی است. هنگام استفاده از قضیه هم پاسخی برای منبع ولتاژ مستقل گامهای زیر طی میشود:
- منبع ولتاژ مستقل در محل قبلی اتصال کوتاه میشود. به عبارت دیگر، آن را از مدار بر میداریم و دو سر آن را با یک سیم اتصال کوتاه میکنیم.
- پلاریته منبع ولتاژ مستقل در محل جدید مطابق با پلاریته جریان شاخه است. پلاریته طوری درنظر گرفته میشود که جریان از قطب منفی منبع ولتاژ وارد و از قطب مثبت خارج شود.
مثالی از قضیه هم پاسخی برای منبع ولتاژ مستقل
حال با یک مثال قضیه را بیشتر توضیح میدهیم. مدار الکتریکی زیر را در نظر بگیرید. این مدار شامل یک منبع ولتاژ مستقل 22 ولتی و سه مقاومت 4، 8 و 12 اهمی است که در اینجا منظور از شاخه nام، مقاومت 12 اهم است که جریان آن را با $$I$$ و جریان منبع مستقل را با $$ I _ {in} $$ نشان میدهیم. در قدم اول این جریان را محاسبه میکنیم.
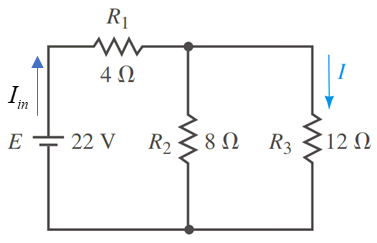
ابتدا مقاومت دو سر منبع ولتاژ را بدست میآوریم:
$$ R_{in}=4\Omega+8\Omega\parallel12\Omega=4+\frac{8 \times12}{8+12}=8.8\Omega$$
سپس جریان عبوری از منبع ولتاژ مستقل را محاسبه میکنیم:
$$I_{in}=\frac{E}{R_{in}}=\frac{22}{8.8}=2.5A$$
دقت کنید که مقاومتهای 12 و 8 اهم یک مدار مقسم جریان را تشکیل میدهند. جریان مقاومت 12 اهم از رابطه زیر بدست میآید:
$$I=\frac{R_{2}}{R_{2}+R_{3}}\times I_{in}=\frac{8}{8+12}\times 2.5=1A$$
حال قضیه همپاسخی را به مدار اعمال میکنیم. منبع ولتاژ مستقل اتصال کوتاه و به صورت سری با مقاومت 12 اهم (همان محل جریان $$I$$ در مدار قبلی) قرار داده میشود. مدار جدید در شکل زیر نمایش داده شده است.
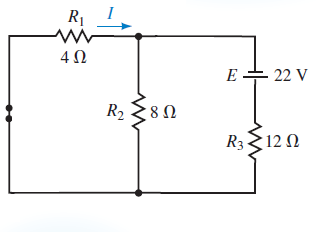
برای محاسبه جریان $$I$$ در مدار جدید، باز هم ابتدا مقاومت دو سر منبع ولتاژ مستقل را محاسبه میکنیم:
$$R_{in}=12\Omega+8\Omega\parallel4\Omega=12+\frac{8 \times 4}{8+4}=\frac{44}{3}\Omega$$
:سپس جریان منبع مستقل به صورت زیر محاسبه میشود
$$I_{in}=\frac{E}{R_{in}}=\frac{22}{\frac{44}{3}}=1.5A$$
برای محاسبه جریان $$I$$، دقت کنید که این بار مقاومتهای 4 و 8 اهم مقسم جریان تشکیل میدهند. جریان مقاومت 4 اهم (محل منبع ولتاژ مستقل در مدار قبلی) به صورت زیر تعیین میشود:
$$I=\frac{R_{2}}{R_{2}+R_{1}} \times I_{in}=\frac{8}{8+4} \times 1.5=1A$$
کاملا واضح است که این جریان برابر جریان مقاومت 12 اهم در مدار اولی است. بنابراین با این مثال، قضیه همپاسخی برای منابع ولتاژ مستقل اثبات میشود.
قضیه هم پاسخی برای منابع جریان مستقل
فرض کنید منبع جریان مستقل یک مدار الکتریکی در گره nام آن ولتاژ الکتریکی $$V$$ را تولید کند (منظور از گره محل اتصال مشترک دو یا چند المان مختلف مدار است). حال اگر محل منبع جریان مستقل را به گونهای تغییر دهیم که از محل اولیه برداشته شده و به گره nاُم متصل شود، آنگاه منبع جریان مستقل (مستقر شده در محل جدید) در محل قبلی خود ولتاژی تولید میکند که دقیقا برابر با ولتاژ $$V $$ است. این ولتاژ، همان ولتاژ گره nام ناشی از منبع جریان مستقل در محل قبلی است.
هنگام اعمال این قضیه به مدارهای الکتریکی گامهای زیر طی میشود:
- منبع جریان مستقل از مدار برداشته شده و دو سر آن مدار باز میشود.
- پلاریته منبع جریان در گره جدید به صورتی است که با پلاریته ولتاژ آن گره در مدار قبلی همخوانی داشته باشد. به عبارت دیگر، جهت منبع جریان مستقل، واردشونده از قطب مثبت ولتاژ است.
مثالی از قضیه هم پاسخی برای منبع جریان مستقل
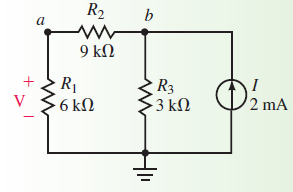
در ادامه از طریق یک مثال عددی، درستی این قضیه اثبات خواهد شد. مدار الکتریکی زیر را در نظر بگیرید. مدار شامل یک منبع جریان مستقل 2 میلیآمپر و سه عدد مقاومت 6، 9 و 3 کیلواهم است. گره مورد بررسی در این مدار همان گره b است که ولتاژی برابر با $$V$$ دارد.
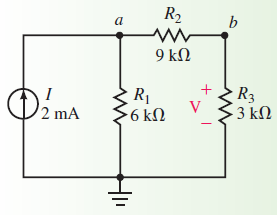
به منظور محاسبه ولتاژ گره b، ابتدا مقاومت ورودی محاسبه میشود:
$$R_{in}=(9K\Omega+3K\Omega)\parallel6K\Omega=\frac{12 \times 6}{12+6}=4K\Omega$$
سپس ولتاژ گره a به سادگی قابل محاسبه است:
$$V_{b}=R_{in} \times I=4K\Omega \times 2mA=8V$$
دقت کنید که مقاومتهای 3 و 9 کیلواهم یک مدار مقسم ولتاژ تشکیل میدهند. بنابراین ولتاژ گره b، یعنی $$V$$ به صورت زیر تعیین میشود:
$$V_{b}=\frac{R_{3}}{R_{3}+R_{2}} \times V_{a}=\frac{3}{3+9} \times 8=2V$$
حال برای اعمال قضیه همپاسخی منبع جریان مستقل از محل اولیه برداشته شده و به گره b متصل میشود. توجه کنید که دو سر منبع جریان به همان دو نقطهای متصل میشود که اختلاف ولتاژ گره b از زمین اندازهگیری شده است. در شکل بالا ولتاژ $$V$$ بین گره b و گره زمین اندازهگیری شده است، پس دو سر منبع جریان به این دو گره متصل خواهد شد. همچنین بعد از برداشتن منبع جریان مستقل دو سر آن مدار باز باقی میماند. مدار جدید مطابق شکل زیر خواهد بود. باز هم دقت کنید که پلاریته مثبت ولتاژ الکتریکی در محل قبلی منبع جریان، همان گرهای است جریان مدار قبلی به آن وارد شده بود.
برای محاسبه ولتاژ $$V$$، مجدداً مقاومت ورودی (مقاومت دو سر منبع جریان مستقل) را اندازهگیری میکنیم:
$$R_{in}=(9K\Omega+6K\Omega)\parallel3K\Omega=\frac{15 \times 3}{15+3}=2.5K\Omega$$
اکنون ولتاژ گره b به راحتی قابل محاسبه است:
$$V_{b}=R_{in} \times I=2.5K\Omega \times 2mA=5V$$
حال در مدار جدید مقاومتهای 6 و 9 کیلواهم یک مدار مقسم ولتاژ را تشکیل میدهند. ولتاژ گره a که همان ولتاژ $$V$$ است برابر است با:
$$V_{b}=\frac{R_{1}}{R_{1}+R_{2}} \times V_{a}=\frac{6}{6+9} \times 5=2V$$
واضح است که این مقدار همان ولتاژی است که در مدار اول و در گره b داشتیم.
اگر این مطلب برای شما مفید بوده است، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای مهندسی برق
- آموزش مدارهای الکتریکی ۱
- مجموعه آموزشهای مهندسی الکترونیک
- آموزش حل تمرین مدارهای الکتریکی ۱
- قضیه میلمن در مدار — به زبان ساده
- تحلیل گره — به زبان ساده
- تحلیل مش — به زبان ساده
^^










