تبدیل کسر به اعشار — به زبان ساده + حل تمرین و مثال

در آموزش‌های پیشین مجله فرادرس، با ضرب و تقسیم کسرها آشنا شدیم. همچنین، در آموزش «اعداد اعشاری — به زبان ساده (+ دانلود فیلم آموزش گام به گام)» مطالبی را درباره اعداد اعشاری بیان کردیم. در این آموزش، می‌خواهیم ببینیم که روش تبدیل کسر به اعشار چگونه است.

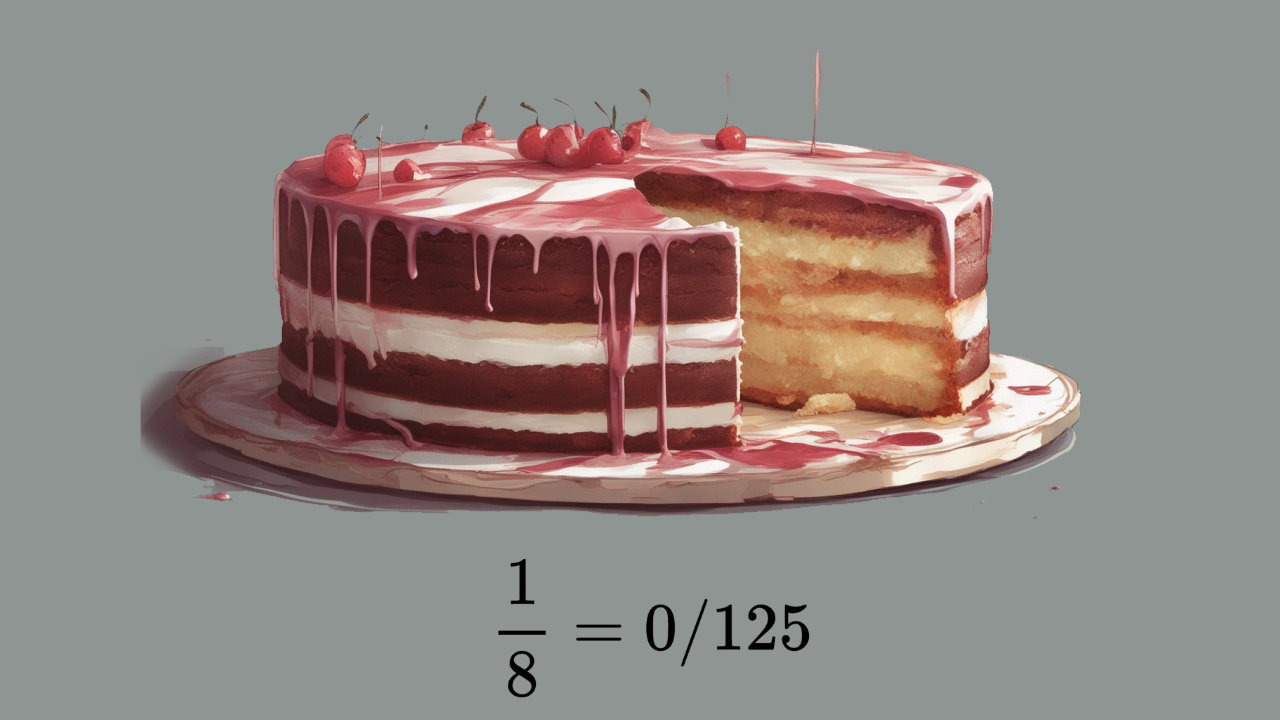
عدد اعشاری چیست؟

اَعشار جمع کلمه عربی عُشر (به‌معنی یک‌دهم) است. به همین دلیل است که اعشار معادل با یک‌دهم‌ها است. چیزی که ما در اعداد اعشاری با آن سر و کار داریم، همین یک‌دهم‌ها هستند که اعداد اعشاری را می‌سازند. برای مثال، اعداد $$ 1.5 $$، $$ 2.8$$، $$ 0.9$$، $$-0.01$$ و... اعدادی اعشاری هستند.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

عدد کسری چیست؟

در مطالب قبلی از سری مطالب ریاضی مجله فرادرس با اعداد صحیح آشنا شدیم. در این مطلب، با کسرها آشنا می‌شویم. کسرها اعدادی هستند که با تقسیم تعریف می‌شوند و برای نشان دادن هر تعداد از قسمت‌های مساوی یک چیز به‌کار می‌روند. در واقع، کسرها اعدادی حقیقی به‌فرم $$\frac p  q $$ هستند که در آن‌ها $$ p $$ و $$ q $$ اعدادی صحیح‌ هستند. عدد $$p$$ صورت کسر و عدد $$ q$$  مخرج کسر نامیده می‌شود. بنابراین، در کسر $$ \frac 23$$ عدد ۲ صورت و عدد ۳ مخرج کسر است و آن را «دو سوم» می‌خوانیم.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

تبدیل کسر به اعشار

تبدیل کسر به اعشار یعنی اینکه معادل اعشاری عدد کسری را بیابیم. اما چگونه این کار را انجام دهیم؟ برای تبدیل کسر به اعشار، ابتدا باید مخرج کسر با به یکی از اعداد $$10$$، $$100$$، $$1000$$ و... تبدیل کنیم. اما دلیل این کار چیست؟ در ابتدای متن گفتیم که وقتی با اعشار کار می‌کنیم، با دهم‌ها و صدم‌ها و هزارم‌ها و... سر و کار داریم. اگر دقت کرده باشید، وقتی یک عدد اعشاری را می‌خوانید، پایان آن به دهم، صدم، هزارم و... ختم می‌شود. در واقع، عدد اعشاری، یک عدد کسری است که مخرج آن ضریب $$ 10 $$ است. بنابراین، کار ما در تبدیل کسر به اعشار، نوشتن کسر با مخرجی است که ضریب $$10$$ باشد.

فیلم آموزش ریاضی – پایه هشتم در فرادرس

کلیک کنید

برای مثال، می‌خواهیم کسر $$\frac {4}{10} $$ را به عدد اعشاری تبدیل کنیم. می‌بینیم که مخرج این کسر، مضربی از عدد $$ 10 $$ است. بنابراین، نیازی به تبدیل مخرج نیست. اما این عدد را چگونه بنویسیم؟ می‌بینیم که مخرج $$10$$ است و $$ 4 $$ نیز کوچک‌تر از $$ 10 $$ است. یک رقم اعشار از راست جدا می‌کنیم و عدد $$4$$ را در سمت راست آن قرار می‌دهیم. سمت چپ اعشار را نیز $$ 0$$ می‌گذاریم، چون مخرج از صورت بزرگ‌تر بوده است. پس، عدد $$ \frac {4}{10}$$‌ به‌صورت اعشاری زیر نوشته می‌شود:

۰٫۴

به‌عنوان یک مثال دیگر، کسر $$ \frac {236}{100} $$ را در نظر بگیرید. می‌خواهیم این کسر را به اعشار تبدیل کنیم. می‌بینیم که مخرج کسر از صورت آن کوچک‌تر است. در چنین حالتی، ابتدا صورت کسر را می‌نویسیم:

۲۳۶

سپس به مخرج کسر نگاه می‌کنیم. می‌بینیم که عدد ۱۰۰ است. بنابراین، دو رقم اعشار از سمت راست جدا می‌کنیم و جواب نهایی به‌‌صورت زیر خواهد بود:

۲٫۳۶

این عدد را این‌گونه می‌خوانیم: دو و سی‌وشش صدم؛ یعنی دو تا ۱۰۰ تایی و ۳۶ تا از ۱۰۰.

اکنون کسر $$ \frac {236}{10}$$ را درنظر بگیرید. مانند مثال قبل، ابتدا عدد صورت را می‌نویسیم:

۲۳۶

سپس، می‌بینیم که عدد مخرج $$10$$ است. بنابراین، از راست یک رقم اعشار جدا می‌کنیم. بنابراین، کسر $$ \frac {236}{10}$$ به‌صورت اعشاری زیر در خواهد آمد:

۲۳٫۶

این عدد را این‌گونه می‌خوانیم: ۲۳ و ۶ دهم؛ یعنی ۲۳ تا ۱۰ تایی و ۶ تا از ۱۰ تا.

در انتها، مثال‌های متنوعی را حل می‌کنیم تا تسلطتان بر این موضوع افزایش یابد.

تبدیل اعشار به کسر

برای تبدیل اعداد اعشاری به اعداد کسری کافی است همان چیزی را که می‌خوانیم، بنویسیم. عدد ۰٫۲۵ را در نظر بگیرید. این عدد را به صورت «بیست‌وپنج صدم» یا بیست‌وپنج تا از صد تا می‌خوانیم و آن را به شکل کسری $$ \frac {25} { 100} $$ می‌نویسیم. به همین ترتیب، چند مثال زیر را نیز داریم:

• ۰٫۱ برابر است با $$ \frac {1} { 10} $$
• ۰٫۰۱ برابر است با $$ \frac {1} { 100} $$
• ۰٫۰۰۱ برابر است با $$ \frac { 1 } { 1000} $$
• ۰٫۵۴ برابر است با $$ \frac {54}{100}$$
• ۰٫۰۳۲ برابر است با $$ \frac{32}{1000}$$

حال عدد اعشاری ۲٫۳۵ را در نظر بگیرید. این عدد را به صورت «دو و سی‌وپنج صدم» می‌خوانیم و آن را به شکل کسری زیر نمایش می‌دهیم:

$$ 2\frac {35}{100}$$

در واقع، $$ 2$$ واحد کامل و کسر $$ \frac{35}{100}$$ را داریم.

حال می‌خواهیم کسر $$ \frac {51}{100}$$ را به صورت یک عدد اعشاری بنویسیم. این کسر «پنجاه‌ویک تا از صد تا» را نشان می‌دهد. واحد کامل نیز نداریم، به همین دلیل آن را به صورت 0٫۵۱ می‌نویسیم.

مثال‌های تبدیل کسر به اعشار

در این بخش، چند مثال را از تبدیل کسر به اعشار حل می‌کنیم.

فیلم آموزش ریاضی پایه هفتم در فرادرس

کلیک کنید

مثال اول تبدیل کسر به اعشار

کسر $$ \frac 34 $$ را به اعشار تبدیل کنید.

حل: می‌بینیم که مخرج کسر یکی از اعداد مضرب $$10$$، یعنی $$10$$، $$ 100$$، $$1000$$ و... نیست. بنابراین، باید مخرج را به مضربی مناسب از $$ 10 $$ تبدیل کنیم. با ضرب مخرج در عدد $$ 25$$، می‌توانیم آن را به $$ 100 $$ تبدیل کنیم. دقت کنید که هنگام ضرب یک عدد در مخرج، حتماً باید آن را در صورت نیز ضرب کنیم تا اثر ضرب مخرج خنثی شود. بنابراین، داریم:

$$ \large \frac 34 = \frac {3 \times 25}{4 \times 25 } = \frac {75}{100} $$

بنابراین، کسر $$ \frac 34 $$ معادل با کسر $$ \frac { 75 } { 100 } $$ است. اکنون مخرج این کسر مضربی از $$ 10 $$ است و می‌توانیم آن را به اعشار تبدیل کنیم. بدین منظور، عدد $$75 $$ را می‌نویسیم و از سمت راست، دو رقم (تعداد صفرهای $$100$$) را از آن جدا می‌کنیم. در نهایت، عدد اعشاری معادل کسر $$ \frac 34 $$، برابر خواهد بود با:

۰٫۷۵

مثال دوم تبدیل کسر به اعشار

کسر $$ \frac 9 2 $$ را به یک عدد اعشاری تبدیل کنید.

حل: ابتدا باید مخرج را به عددی تبدیل کنیم که مضرب $$10$$ است. اگر $$ 2 $$ را در $$10$$ ضرب کنیم، چنین چیزی محقق می‌شود. پس کسر را به‌صورت زیر می‌نویسیم:‌

$$ \large \frac 9 2 = \frac {9 \times 5 } { 2 \times 5 } = \frac {45}{10}$$

اکنون، به‌اندازه تعداد صفرهای $$10$$، یعنی یک رقم، از سمت راست جدا می‌کنیم و کسر به‌صورت زیر درمی‌آید:

۴٫۵

اگر دقت کنید، $$ 9 $$ را به $$ 2 $$ قسمت تقسیم کنیم، حاصلش می‌شود $$ 4.5 $$.

مثال سوم تبدیل کسر به اعشار

کسر $$ \frac 3 6 $$ را به اعشار تبدیل کنید.

حل: برای تبدیل کسر به اعشار، مخرج باید $$10$$، $$100$$، $$1000$$ و... باشد. اما در اینجا مخرج $$ 6 $$ است. اما مخرج $$ 6 $$ را نمی‌توانیم به ضرب به یک عدد مضرب $$ 10$$ تبدیل کنیم. بنابراین، کسر را ساده می‌کنیم. هم صورت و هم مخرج را می‌توان بر $$ 3 $$ تقسیم کرد:

$$ \large \frac 3 6 = \frac {3 \div 3 }{6 \div 3 } = \frac 12 $$

اکنون می‌توانیم با ضرب صورت و مخرج در $$5$$، مخرج را به $$10$$ تبدیل کنیم:

$$ \large \frac 12 = \frac {1 \times 5 } {2 \times 5 } = \frac {5}{10} $$

اکنون، عدد $$5$$ را می‌نویسیم و از راست یک رقم اعشار را جدا می‌کنیم:

۰٫۵

اگر دقت کنید، یک‌دوم همان تقسیم یک بر دو است که نیم می‌شود.

مثال چهارم تبدیل کسر به اعشار

کسر $$ 2\frac 18 $$ را به عدد تبدیل کنید.

حل: ابتدا کسر را به یک کسر متعارفی تبدیل می‌کنیم:

$$ \large 2\frac 18 = \frac {2\times 8 + 1}{8} = \frac {17 }{8}$$

مخرج این کسر $$ 8$$ است و باید آن را به یک عدد مضرب $$ 10$$ تبدیل کنیم. با ضرب آن در $$ 125$$ به $$ 1000$$ می‌رسیم که مضرب $$ 10 $$ است. بنابراین، خواهیم داشت:

$$ \large \frac {17 } {8} = \frac {17 \times 125}{8\times 125} = \frac {2125}{1000}$$

اکنون، صورت کسر را می‌نویسیم، و از راست سه رقم اعشار را جدا می‌کنیم:

۲٫۱۲۵

بنابراین:

$$ 2 \frac 18 = 2.125 $$

مثال پنجم تبدیل کسر به اعشار

کسر $$ \frac {3}{16}$$ را به اعشار تبدیل کنید.

حل: باید ببینیم عدد $$ 16 $$ را در چه عددی ضرب کنیم تا حاصل مضربی از $$ 10 $$ شود. اگر از ماشین حساب کمک بگیریم، با کمی سعی و خطا به عدد $$ 625 $$ می‌رسیم و خواهیم داشت:‌

$$ \large \frac {3 } {16} = \frac {625 \times 3}{625\times 16} = \frac {1875}{10,000}$$

اکنون، عدد صورت، یعنی $$ 1875$$ را می‌نویسیم، و از راست چهار رقم اعشار را جدا می‌کنیم:

۰٫۱۸۷۵

آزمون سنجش یادگیری تبدیل کسر به اعشار

در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث تبدیل کسر به اعشار را با طرح سوال‌های چندگزینه‌ای می‌سنجیم. پس از جواب دادن به تمام سوال‌ها، نتیجه آزمون برای شما به نمایش درمی‌آید.