تابع فعالسازی در شبکه های عصبی — معرفی توابع Activation Functions

در سال‌های اخیر، یادگیری عمیق و به بیان جزئی‌تر، شبکه های عصبی یکی از مهم‌ترین و داغ‌ترین مباحث از شاخه هوش مصنوعی به حساب می‌آید. پژوهشگران بسیاری در سراسر دنیا، تحقیقات خود را به این موضوع جذاب اختصاص داده‌اند. روزانه، معماری‌های جدیدی از شبکه های عصبی پیشنهاد و راه‌حل‌های بسیاری به منظور بهبود در عملکرد ساختار مدل‌های عمیق موجود ارائه می‌شوند. یکی از اجزای اصلی شبکه های عصبی، تابع فعالسازی (Activation Function) است که نقش آن در روال یادگیری شبکه عصبی، تفکیک اطلاعات مهم داده‌های ورودی از اطلاعات بی‌اهمیت است. در مقاله حاضر به تعریف تابع فعالسازی در شبکه های عصبی پرداخته و توضیحی از انواع توابع فعالسازی (Activation Functions) در شبکه های عصبی ارائه شده است.

شبکه عصبی چیست ؟

«شبکه عصبی مصنوعی» (Artificial Neural Network) واحد عملیاتی در یادگیری عمیق محسوب می‌شود که برای حل مسائل پیچیده داده-محور، رفتاری شبیه به رفتار مغز انسان دارد. از شبکه عصبی در حوزه‌های مختلف مبتنی‌بر هوش مصنوعی، از تشخیص گفتار و تشخیص چهره گرفته تا مسائل مربوط به مراقبت‌های بهداشتی و بازاریابی استفاده می‌شود. در شبکه عصبی داده‌های ورودی با عبور از لایه‌های مختلف و گره‌های مصنوعی متصل به هم، پردازش می‌شوند تا در نهایت خروجی مورد انتظار تولید شود.

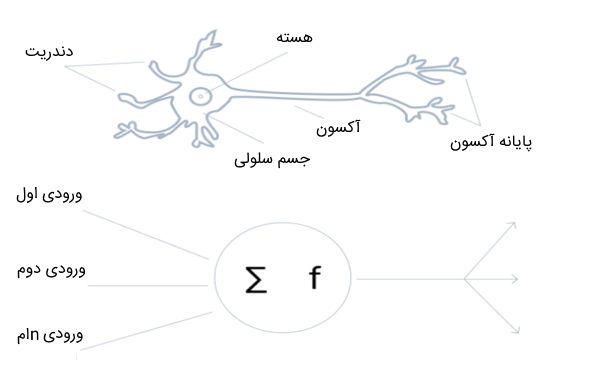
اجزای شبکه های عصبی مصنوعی کدامند ؟

درک مفهوم شبکه های عصبی و نحوه عملکرد آن‌ها دشوار است و بحث درباره تابع‌های فعالسازی در شبکه های عصبی وضعیت را پیچیده‌تر می‌کند. بنابراین، در ابتدا بهتر است که به‌طور سریع و ساده، توضیحی از ساختار معماری شبکه عصبی و اجزای آن ارائه شود و سپس به عملکرد تابع فعالسازی در شبکه های عصبی و انواع آن‌ها پرداخته شود. اجزای اصلی شبکه عصبی عبارت‌اند از:

• گره (Node)
• لایه (Layer)

در ادامه این مقاله، به شرح جامع اجزای اصلی شبکه عصبی پرداخته شده است.

گره یا Node در شبکه های عصبی چیست ؟

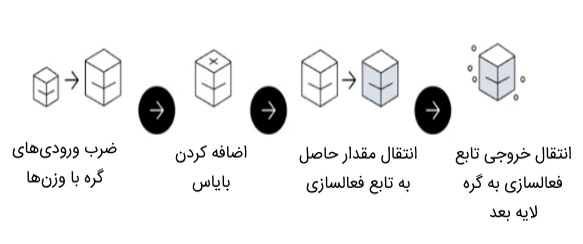
شبکه های عصبی از واحدهای مستقلی به نام گره یا نود ساخته شده‌اند که این گره‌ها رفتاری شبیه به رفتار مغز انسان دارند. به عبارتی، گره‌های شبکه های عصبی، عملکردی مشابه با عملکرد نورون‌های مغز انسان دارند که مجموعه‌ای از سیگنال‌های ورودی (محرک‌های خارجی) را دریافت می‌کنند. گره، از اجزای مختلفی ساخته شده است؛ این اجزا در ادامه فهرست شده‌اند:

• ورودی گره در شبکه عصبی
• وزن گره در شبکه عصبی
• تابع فعالسازی در شبکه عصبی
• بایاس گره در شبکه عصبی

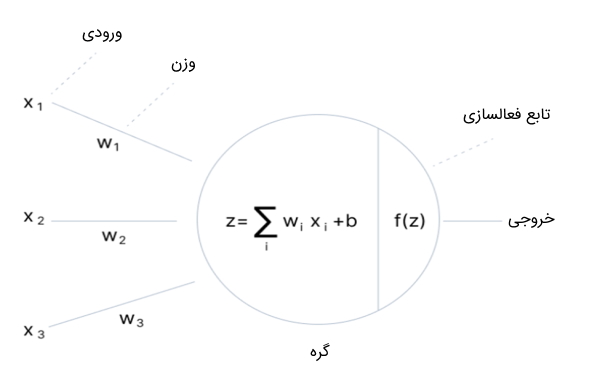
در ادامه، به توضیح هر یک از اجزای تشکیل‌دهنده گره در شبکه های عصبی پرداخته شده است.

ورودی گره در شبکه های عصبی مصنوعی

ورودی گره شامل مجموعه‌ای از ویژگی‌ها است که برای روند یادگیری شبکه عصبی، به مدل وارد می‌شوند. به عنوان مثال، در مسئله تشخیص اشیاء، ورودی گره، آرایه‌ای از مقادیر پیکسل‌های تصاویر است.

وزن گره در شبکه های عصبی

از وزن‌ها به منظور تعیین میزان اهمیت ویژگی‌های ورودی گره استفاده می‌شود. به عبارتی، با اعمال ضرب داخلی یا اسکالر مقدار ورودی گره و ماتریس وزن، میزان اهمیت هر ویژگی ورودی مشخص می‌شود. به عنوان مثال، در مسئله تحلیل احساسات، وزن کلمات منفی و مثبت از وزن سایر کلمات بیشتر است و شبکه عصبی با توجه به کلمات با وزن‌های بیشتر، تحلیل احساسات جملات را انجام می‌دهد.

تابع فعالسازی در شبکه های عصبی

در تابع فعالسازی (Activation Function) که به آن «تابع انتقال» هم گفته می‌شود، در ابتدا مقادیر ورودی گره با یکدیگر ترکیب می‌شوند تا خروجی حاصل به تابع فعالسازی شبکه های عصبی منتقل شود. به عبارتی، مقادیر حاصل از ضرب وزن‌ها با ویژگی‌های ورودی با یکدیگر جمع می‌شوند و مقدار حاصل به تابع فعالسازی منتقل می‌شود.

تابع فعالسازی در شبکه های عصبی ترکیب خطی ورودی‌ها را غیرخطی می‌کند و مقادیر ورودی را براساس نوع تابع فعالسازی به فضا با بازه مشخصی نگاشت می‌کند. در بخش‌های بعدی این مقاله با جزئیات به تعریف تابع فعالسازی در شبکه های عصبی ، عملکرد تابع فعالسازی، دلیل استفاده از تابع فعالسازی و انواع تابع فعالسازی در شبکه های عصبی پرداخته شده است.

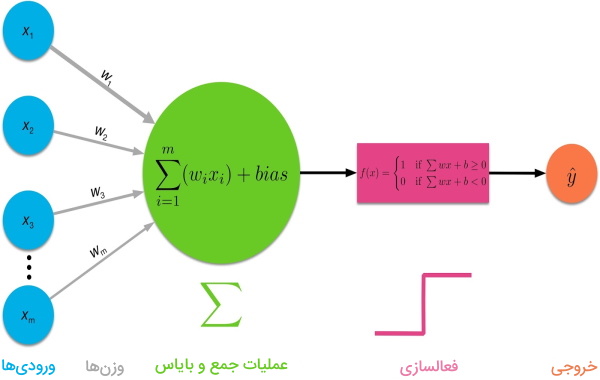
بایاس در شبکه های عصبی

نقش بایاس در شبکه عصبی این است که خروجی نهایی تابع فعالسازی را تغییر دهد. نقش بایاس مشابه نقش مقدار ثابت در تابع خطی است.

لایه در شبکه های عصبی مصنوعی

زمانی که در شبکه عصبی، چندین گره در یک ردیف کنار هم قرار بگیرند، یک لایه را تشکیل می‌دهند. زمانی که چندین لایه از گره‌ها در کنار یکدیگر قرار بگیرند، شبکه عصبی ساخته می‌شود. در ادامه به توضیح انواع لایه‌ها در شبکه عصبی پرداخته می‌شود.

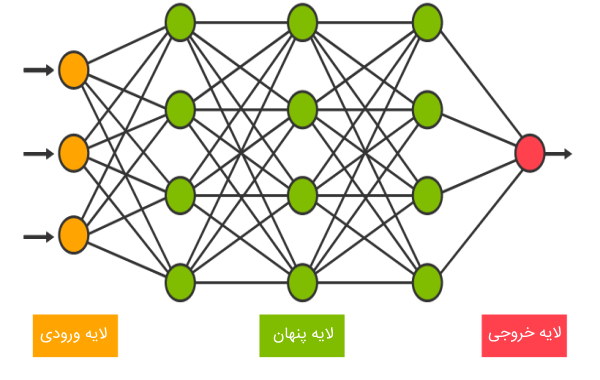
لایه ورودی در شبکه عصبی

در شبکه های عصبی، همیشه یک لایه ورودی برای دریافت ویژگی‌های ورودی وجود دارد. به عبارتی، اطلاعات دنیای خارج، نظیر اطلاعات موجود در فایل CSV یا سرویس وب، از طریق این لایه وارد شبکه عصبی می‌شوند. در این لایه، هیچ عملیات محاسباتی انجام نمی‌شود و صرفاً اطلاعات (ویژگی‌ها) از طریق این لایه، به لایه‌های پنهان منتقل می‌شوند. تعداد گره‌های لایه ورودی به ابعاد داده‌های ورودی بستگی دارند.

لایه پنهان در شبکه عصبی

این لایه، بین لایه ورودی و لایه خروجی قرار دارد و به همین دلیل به این لایه، لایه میانی یا پنهان گفته می‌شود. از واژه «پنهان» (Hidden) برای نامگذاری لایه‌های میانی شبکه عصبی استفاده می‌شود زیرا سیستم‌های بیرونی به این لایه دسترسی ندارند و لایه پنهان، به عنوان بخش خصوصی شبکه عصبی تلقی می‌شود.

شبکه عصبی می‌تواند لایه پنهان نداشته باشد؛ اما برای اکثر تسک‌ها، حداقل از یک لایه پنهان برای شبکه عصبی استفاده می‌شود. هر چقدر تعداد لایه‌های پنهان شبکه عصبی بیشتر باشد، میزان بار محاسباتی شبکه بیشتر می‌شود.

به طور معمول، از تابع فعالسازی مشابهی برای تمامی لایه‌های پنهان شبکه عصبی استفاده می‌شود؛ با این حال، براساس هدف و کاربرد شبکه عصبی، تابع فعالسازی لایه خروجی شبکه معمولاً با سایر توابع فعالسازی لایه‌های پنهان مغایرت دارد.

تعداد گره‌های لایه‌های پنهان در شبکه عصبی با یکدیگر برابر هستند. برای تشخیص تعداد گره‌های مناسب در لایه پنهان می‌توان از فرمول زیر استفاده کرد. مقدار ضریب فاکتور در فرمول زیر، عددی بین 0 و 10 است که برای جلوگیری از overfit شدن شبکه از آن استفاده می‌شود.

$$Number\ of\ Neurons = \frac{Trading \ Data \ Samples}{Factors \times (Input\ Neurons + Output \ Neurons)}$$

لایه خروجی در شبکه عصبی

این لایه، خروجی نهایی شبکه عصبی را تولید می‌کند. در شبکه های عصبی، وجود یک لایه خروجی الزامی است. لایه خروجی، ورودی خود را از لایه قبل خود دریافت می‌کند و با استفاده از گره‌های خود، محاسباتی روی ورودی‌ها انجام می‌دهد و مقدار خروجی شبکه عصبی را محاسبه می‌کند.

تعداد گره‌های لایه خروجی به هدف شبکه عصبی بستگی دارد. چنانچه از شبکه عصبی برای محاسبه مقدار رگرسیون استفاده می‌شود، تنها یک گره در لایه خروجی در نظر گرفته می‌شود. اگر از شبکه عصبی به منظور دسته‌بندی داده‌ها استفاده شود، بسته به این که تابع فعالسازی گره‌ها از چه نوعی باشند، ممکن است به بیش از یک گره در لایه خروجی احتیاج باشد. در این حالت، هر یک از گره‌های لایه خروجی، مقداری را به ازای هر دسته تعریف شده در مسئله محاسبه می‌کند.

مفاهیم مرتبط با توابع فعالسازی در شبکه های عصبی

برای درک عملکرد توابع فعالسازی در شبکه های عصبی لازم است به توضیح چهار مفهوم مهم و اساسی در شبکه عصبی پرداخته شود. این چهار مفهوم مرتبط با عملکرد توابع فعالسازی در ادامه فهرست شده‌اند:

• «پیش‌خور | رو به جلو» (Feedforward)
• «انتشار رو به عقب | پس انتشار» (Backpropagation)
• «محوشدگی گرادیان» (Vanishing Gradient)
• «انفجار گرادیان» (Exploding Gradient)

در ادامه این بخش، به توضیح مفاهیم هر یک از این چهار اصطلاح به صورت خلاصه پرداخته می‌شود.

مرحله انتشار پیش خور در شبکه عصبی

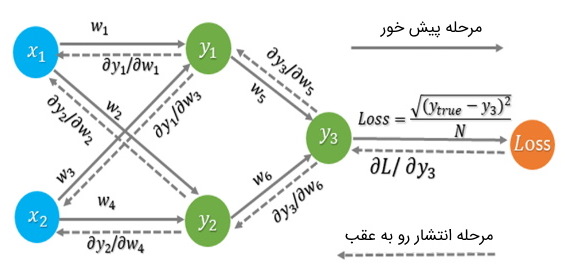
در مرحله انتشار پیش‌خور، جریان اطلاعات، به سمت جلو است. به بیان دیگر، در انتشار پیش‌خور، از طریق لایه ورودی، داده‌ها وارد شبکه می‌شوند و با اعمال محاسبات برروی آن‌ها با استفاده از توابع فعالسازی در لایه‌های پنهان، خروجی هر لایه به لایه بعد خود منتقل می‌شود تا در نهایت خروجی شبکه در لایه آخر مشخص شود. در مرحله انتشار پیش‌خور، تابع فعالسازی شبکه های عصبی به عنوان «درگاه» (Gate) تلقی می‌شود که ورودی‌های هر لایه را به لایه بعد ارسال می‌کند.

مرحله انتشار رو به عقب در شبکه عصبی

هدف از مرحله انتشار رو به عقب، کاهش مقدار «تابع هزینه» (Cost | Loss Function) با استفاده از تنظیم مقادیر وزن‌ها و بایاس شبکه است. گرادیان‌های تابع هزینه میزان تغییرات را با توجه به پارامترهایی نظیر تابع فعالسازی، وزن‌ها، بایاس و سایر موارد مربوطه تعیین می‌کنند.

محوشدگی گرادیان در شبکه عصبی

یکی از چالش‌های اصلی در مدت زمان یادگیری شبکه عصبی، رخداد مسئله محوشدگی گرادیان است. هرچقدر تعداد لایه‌های شبکه عصبی بیشتر باشد، احتمال اینکه مقدار گرادیان تابع هزینه به صفر نزدیک‌تر شود، بیشتر می‌شود. در پی این اتفاق، فرآیند یادگیری شبکه عصبی با دشواری روبه‌رو می‌شود. برخی از توابع فعالسازی در شبکه های عصبی، مقادیر ورودی بزرگ خود را به بازه 0 تا 1 نگاشت می‌کنند. به این ترتیب، با اعمال تغییر زیاد در مقدار ورودی، میزان تغییر در مقدار خروجی بسیار اندک خواهد بود. بنابراین، خروجی مقدار مشتق تابع، عددی بسیار کوچک می‌شود.

کوچک بودن خروجی مشتق تابع در شبکه هایی که تعداد لایه‌های پنهان کمی دارند، مشکل‌ساز نیست؛ اما در شبکه های عمیق‌تر در طی روند انتشار رو به عقب، مقدار مشتق گره‌های هر لایه با یکدیگر ضرب می‌شوند. به عبارت دقیق‌تر، چنانچه در n لایه متوالی از تابع فعالسازی استفاده شود که ورودی را به بازه عددی 0 تا 1 تبدیل می‌کند، مقادیر کوچک مشتق‌ها n بار در یکدیگر ضرب می‌شوند؛ همین امر باعث می‌شود مقدار گرادیان به‌صورت نمایی کاهش پیدا کند و به عدد صفر نزدیک شود که به این حالت، محوشدگی گرادیان گفته می‌شود. کوچک شدن مقدار گرادیان باعث می‌شود که پارامترهای شبکه عصبی نظیر مقادیر وزن‌ها و بایاس‌ها در لایه‌های ابتدایی شبکه به‌روزرسانی نشوند و بنابراین یادگیری شبکه به‌درستی انجام نگیرد.

انفجار گرادیان در شبکه عصبی

گرادیان خطا، مقداری است که جهت و مقدار یادگیری را در حین آموزش شبکه عصبی مشخص می‌کند. به عبارتی، از گرادیان به منظور به‌روزرسانی وزن‌های شبکه استفاده می‌شود.

در شبکه های عمیق یا «شبکه های عصبی بازگشتی» (Recurrent Neural Network | RNN) ممکن است مقادیر گرادیان خطا روی هم انباشته شوند و مقادیر گرادیان خیلی بزرگ شوند. این مسئله باعث می‌شود مقدار به‌روزرسانی وزن‌ها بسیار بزرگ شود که همین امر منجر به ناپایداری شبکه خواهد شد. در برخی مواقع، ممکن است مقادیر بزرگ وزن‌ها باعث «سرریز شدن» (Overflow) وزن‌ها و رسیدن به مقادیر NaN شوند.

مسئله انفجار گرادیان در پی رشد نمایی و ضرب مکرر مقادیر گرادیان‌های بزرگ رخ می‌دهد که در این حالت، مقادیر گرادیان‌ها بیشتر از عدد 1 می‌شوند. در پی انفجار گرادیان‌ها، یادگیری شبکه متوقف شده و وزن‌های شبکه به‌روزرسانی نمی‌شوند.

معرفی فیلم های آموزش پایتون

 

سایت فرادرس یک مجموعه آموزشی برای آن دسته از افرادی فراهم کرده است که قصد یادگیری پایتون را دارند. زبان پایتون یکی از زبان‌های مهم در حوزه یادگیری عمیق و یادگیری ماشین است و افراد علاقه‌مند به برنامه نویسی در حوزه هوش مصنوعی و پیاده‌سازی مدل‌های عمیق می‌توانند از مجموعه فیلم‌های آموزشی پایتون استفاده کنند.

این دوره‌های آموزشی شامل فیلم‌های آموزشی مقدماتی تا پیشرفته و پروژه‌محور زبان پایتون می‌شوند. علاقه‌مندان می‌توانند از این دوره آموزشی جامع در راستای تقویت مهارت عمومی خود در برنامه نویسی پایتون استفاده کنند. در تصویر فوق تنها برخی از دوره‌های آموزشی مجموعه آموزش پایتون فرادرس نمایش داده شده‌اند.

• برای دسترسی به همه آموزش های پایتون فرادرس + اینجا کلیک کنید.

تابع فعالسازی در شبکه های عصبی چیست و چه کاربردی دارد؟

همان‌طور که در بخش قبل توضیح داده شد، تابع فعالسازی جزء اصلی گره‌های شبکه عصبی محسوب می‌شود. توابع فعالسازی در شبکه های عصبی تعیین می‌کنند که آیا گره باید فعال یا غیرفعال باشد. به عبارتی دیگر، این توابع، با استفاده از محاسبات ساده ریاضی مشخص می‌کنند که آیا ورودی گره برای شبکه اهمیت دارد یا باید آن را نادیده گرفت.

نقش تابع فعالسازی در شبکه های عصبی این است که با استفاده از مقادیر ورودی گره، مقداری در خروجی تولید کند. به بیان جزئی‌تر، تابع فعالسازی مقدار مجموع ورودی وزن‌دار گره را به مقادیری بین 0 تا 1 یا 1- تا 1 (بسته به تابع فعالسازی) نگاشت می‌کند. سپس، این تابع، مقدار نهایی خود را به لایه بعد منتقل می‌کند. به همین دلیل، به این تابع، تابع انتقال نیز گفته می‌شود.

در ادامه این مطلب، به انواع توابع فعالسازی در شبکه های عصبی پرداخته می‌شود و ویژگی‌های هر یک از این توابع با یکدیگر مورد مقایسه قرار می‌گیرند.

انواع توابع فعالسازی در شبکه های عصبی کدامند ؟‌

توابع فعالسازی در شبکه های عصبی را می‌توان به سه دسته کلی تقسیم‌بندی کرد که در زیر فهرست شده‌اند:

• «تابع پله دودویی» (Binary Step Function)
• «تابع فعالسازی خطی» (Linear Activation Function)
• «تابع فعالسازی غیرخطی» (Non-linear Activation Function)

در ادامه مطلب، به توضیح ویژگی‌ها، مزایا و معایب هر یک از این توابع فعالسازی پرداخته می‌شود.

تابع پله دودویی

تابع پله دودویی حد آستانه‌ای را در نظر می‌گیرد که براساس آن تصمیم بگیرد آیا گره باید فعال باشد یا ورودی گره برای شبکه اهمیت ندارد. به عبارتی، ورودی این تابع فعالسازی با مقدار حد آستانه مقایسه می‌شود. اگر مقدار ورودی از مقدار حد آستانه بیشتر باشد، گره فعال خواهد شد در غیر این صورت غیرفعال باقی می‌ماند و خروجی گره به لایه بعد منتقل نمی‌شود.

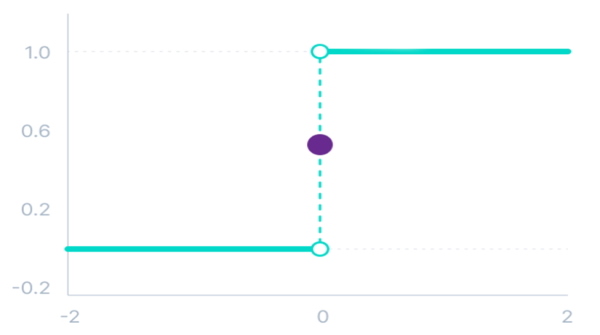
تابع ریاضی این فعالساز به صورت زیر است:

\[
f(x)\colon \biggl\{\begin{array}{@{}r@{\;}l@{}}
0 & for & x<0\\
1 & for & x\geq0
\end{array}\]

تابع پله دودویی دارای محدودیت‌هایی است که در زیر فهرست شده‌اند:

• تابع پله دودویی نمی‌تواند خروجی‌هایی با مقادیر چندگانه تولید کند. به عنوان مثال، نمی‌توان از این تابع برای مسائل دسته‌بندی چند-کلاسه استفاده کرد.
• مشتق تابع پله دودویی برابر با صفر است که این ویژگی، مانعی برای روند انتشار رو به عقب محسوب می‌شود.

تابع فعالسازی خطی

به تابع فعالسازی خطی، «تابع همانی» (Identify Function) نیز گفته می‌شود. این تابع، بر روی مجموع وز‌ن‌دار ورودی، محاسبات انجام نمی‌دهد و این مقدار را بدون هیچ تغییری به لایه بعد منتقل می‌کند.

خروجی این نوع تابع فعالسازی در شبکه های عصبی، به صورت خطی است و نمی‌توان مقدار آن را در بازه‌ای مشخص تعیین کرد. بنابراین از این نوع تابع فقط در مدل‌های رگرسیون خطی استفاده می‌شود.

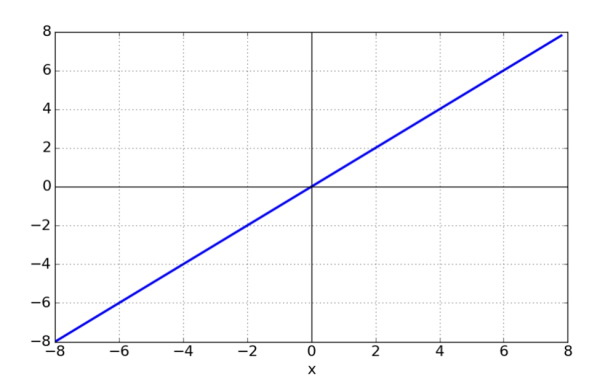
می‌توان تابع ریاضی این فعالساز را به صورت زیر نوشت:

$$f(x) = x$$

تابع فعالسازی خطی، محدودیت‌ها و مشکلات اساسی دارد که در زیر فهرست شده‌اند:

• از این تابع نمی‌توان در مرحله انتشار به عقب استفاده کرد زیرا مشتق این تابع برابر با یک عدد ثابت است و هیچ رابطه‌ای با مقدار ورودی x ندارد.
• نتیجه چندین تابع خطی برروی یک مقدار ثابت ورودی، یکسان است. بنابراین، اهمیتی ندارد شبکه عصبی از چندین لایه پنهان ساخته شده باشد؛ زیرا خروجی تابع فعالسازی در لایه آخر شبکه عصبی برابر با خروجی تابع فعالسازی در لایه اول است.
• زمانی که از پارامترهای زیاد و پیچیده در شبکه عصبی استفاده شده باشد، این نوع تابع فعالسازی عملکرد خوبی نخواهد داشت.

تابع فعالسازی غیرخطی

این نوع توابع بیشترین استفاده را در شبکه های عصبی دارند. تعمیم‌پذیری و تطبیق‌پذیری مدل با انواع مختلف داده با استفاده از توابع فعالسازی غیرخطی آسان می‌شود.

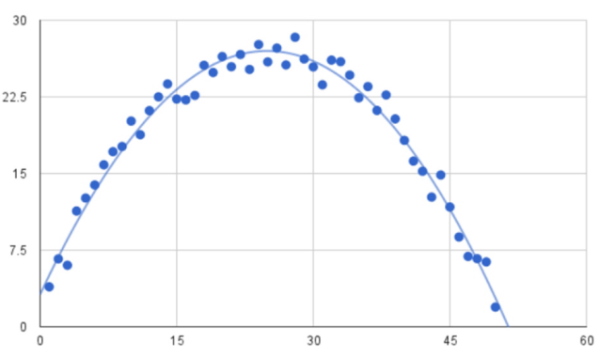
استفاده از توابع فعالسازی غیرخطی در شبکه های عصبی گام اضافه‌تری را به محاسبات هر لایه در مرحله انتشار پیش‌خور اضافه می‌کند؛ اما این گام اضافه‌تر مزیت مهمی دارد. اگر یک شبکه عصبی بدون توابع فعالسازی وجود داشته باشد، هر گره صرفاً برروی ورودی‌های خود با استفاده از مقادیر وزن‌ها و بایاس محاسبات خطی انجام می‌دهد. در این حالت، تعداد لایه‌های پنهان در شبکه عصبی اهمیت ندارند و تمامی لایه‌ها عملکردی مشابه دارند زیرا حاصل ترکیب دو تابع خطی، یک تابع خطی خواهد بود.

با این که در این حالت، شبکه عصبی ساده‌تر است، اما شبکه قادر به انجام وظیفه‌های پیچیده‌تر نخواهد بود و کاربرد شبکه عصبی فقط به مسائل رگرسیون خطی محدود می‌شود.

ویژگی های تابع فعالسازی غیر خطی چه هستند؟

توابع فعالسازی غیرخطی محدودیت‌های تابع‌های فعالسازی خطی را رفع کرده‌اند. ویژگی‌های اصلی این توابع فعالسازی عبارت‌اند از:

• این توابع مشکل مربوط به مرحله انتشار به عقب را حل کردند. به عبارتی، توابع غیرخطی در مرحله انتشار رو به عقب می‌توانند مشخص کنند کدام وزن‌ گره ورودی به تشخیص نهایی مدل می‌تواند کمک بهتری کند.
• با استفاده از این توابع می‌توان مسائل مربوط به خروجی‌های چندگانه را حل کرد. به عبارتی، خروجی توابع غیرخطی، ترکیب غیرخطی از ورودی‌ها است که از لایه‌های متعدد عبور کرده است.

انواع تابع فعالساز غیر خطی چیست؟

توابع فعالسازی غیرخطی در شبکه های عصبی را می‌توان به چندین نوع تقسیم کرد که در ادامه فهرست شده‌اند:

• تابع فعالسازی سیگموئید (Sigmoid | Logistic)
• تابع فعالسازی تابع تانژانت هذلولوی (Tanh | Hyperbolic Tangent)
• تابع فعالسازی یکسوساز (RELUs)
• تابع فعالسازی یکسوساز رخنه‌دار (Leaky RELUs)
• تابع فعالسازی یکسوساز پارامتریک (Parametric RELUs)
• تابع فعالسازی واحدهای خطی نمایی (Exponential Linear Units | ELUss)
• تابع فعالسازی Softmax
• تابع فعالسازی Swish
• تابع فعالسازی واحد خطی خطای گاوسی (Gaussian Error Linear Unit | GELUs)
• تابع فعالسازی واحد خطی مقیاس‌بندی‌شده نمایی (Scaled Exponential Linear Unit | SELUs)

در ادامه مطلب، به توضیح هر یک از انواع توابع فعالسازی غیرخطی و مزایا و معایب آن‌ها پرداخته شده است.

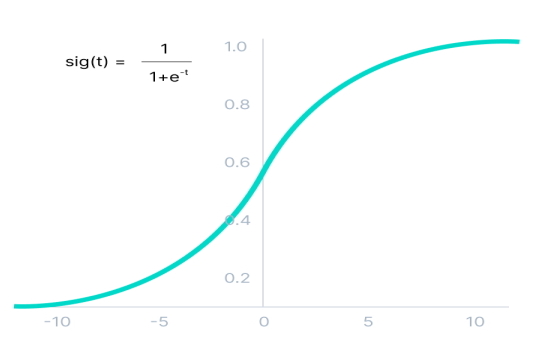
تابع فعالسازی غیرخطی سیگموئید در شبکه های عصبی

این تابع فعالسازی غیرخطی، ورودی خود را به مقداری در بازه 0 تا 1 تبدیل می‌کند. هرچقدر مقدار ورودی بزرگ‌تر باشد، مقدار خروجی این تابع به عدد 1 نزدیک‌تر می‌شود. در حالی‌که اگر مقدار ورودی این تابع خیلی کوچک باشد (عدد منفی)، مقدار خروجی تابع سیگموئید به عدد صفر نزدیک‌تر می‌شود. تابع سیگموید، تابعی «یکنوا» (Monotonic) محسوب می‌شود اما مشتق این تابع، تابع یکنوا نیست.

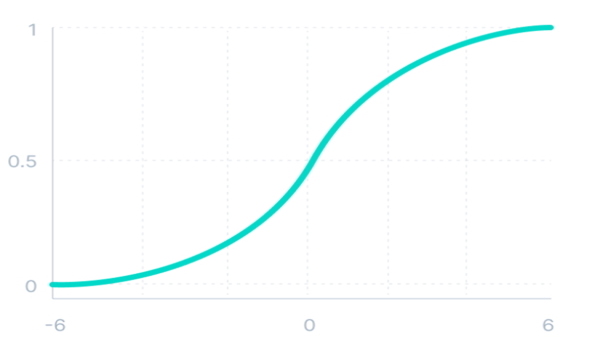
رابطه ریاضی فعالساز سیگموئید به صورت زیر است:

\[f(x) = \frac{1}{1 + e^{-x}}\]

تابع سیگموئید به عنوان یکی از پرکاربردترین توابع فعالسازی غیرخطی محسوب می‌شود. مزایای استفاده از این تابع به شرح زیر هستند:

• معمولاً، از این تابع در مدل‌هایی استفاده می‌شود که خروجی مدل، مقداری احتمالاتی است. از آنجا که مقدار احتمال، عددی بین 0 تا 1 است، تابع سیگموئید بهترین انتخاب برای محاسبه احتمال محسوب می‌شود.
• تابع سیگموئید تابعی مشتق‌پذیر به حساب می‌آید و نمودار خروجی این تابع دارای شیب ملایم به شکل S است.

مهم‌ترین محدودیتی که تابع سیگموئید در شبکه های عصبی ایجاد می‌کند، مسئله محوشدگی گرادیان است که به دلیل مشتق این تابع اتفاق می‌افتد. مشتق تابع فعالسازی سیگموئید در ادامه آمده است :

\[f'(x) = sigmoid(x) * (1 - sigmoid(x))\]

منحنی مربوط به تابع مشتق سیگموئید در تصویر زیر مشاهده می‌شود.

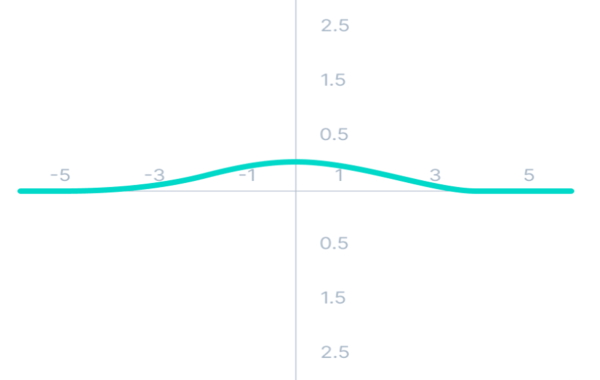
طبق تصویر بالا، مقادیر گرادیان در بازه 3- تا 3 مقدار قابل توجهی دارد و در سایر نواحی، مقدار گرادیان به عدد صفر متمایل می‌شود. در این حالت، مقدار گرادیان این تابع برای مقادیر بیشتر از 3 یا کمتر از 3- بسیار کوچک است. زمانی که مقدار گرادیان به سمت صفر میل می‌کند، یادگیری شبکه متوقف می‌شود که در این حالت، مسئله محوشدگی گرادیان اتفاق می‌افتد. به عبارتی، از آنجا که تابع سیگموئید فضای ورودی خود را به فضای بین 0 تا 1 تبدیل می‌کند، تغییرات بزرگ ورودی این تابع، باعث ایجاد تغییرات کوچک در خروجی می‌شوند و بنابراین، مشتق این تابع مقداری بسیار کوچک خواهد بود.

در شبکه هایی با تعداد لایه‌های کم، این مسئله مشکل‌ساز نیست؛ اما هرچقدر تعداد لایه‌های بیشتری از این تابع فعالسازی در شبکه عصبی استفاده شود، گرادیان تابع هزینه به صفر میل می‌کند و در این حالت، یادگیری شبکه دشوار خواهد شد.

تابع فعالسازی تابع تانژانت هذلولوی در شبکه های عصبی

تابع فعالسازی تانژانت هذلولوی (Hyperbolic Tangent به اختصار Tanh) با تابع فعالسازی سیگموئید بسیار شباهت دارد و منحنی این تابع به S شبیه است. تابع Tanh تابعی یکنواخت محسوب می‌شد اما مشتق آن، تابع یکنواخت نیست. تنها تفاوت این تابع با تابع سیگموئید، بازه خروجی این تابع است که مقدار ورودی خود را به محدوده بین 1- تا 1 نگاشت می‌کند. هرچقدر مقدار ورودی تابع Tanh بزرگ‌تر باشد، مقدار خروجی تابع به عدد 1 نزدیک‌تر خواهد بود و هرچقدر مقدار ورودی این تابع کوچک‌تر باشد، مقدار خروجی تابع به عدد 1- نزدیک‌تر می‌شود.

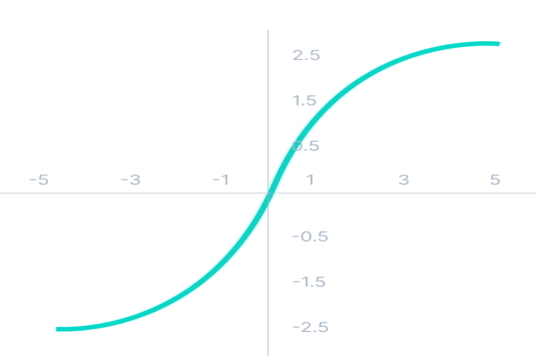
می‌توان رابطه ریاضی Tanh را به صورت زیر نوشت:

$$f(x) = \frac{e^{x}-e^{-x}}{e^{x}+ e^{-x}}$$

مزایای استفاده از تابع Tanh به شرح زیر است:

• تابع Tanh تابعی مشتق‌پذیر است.
• خروجی تابع Tanh در مرکز منحنی برابر با صفر است. به این ترتیب، به‌راحتی می‌توان مقادیر خروجی را به‌صورت مثبت، منفی و خنثی تقسیم کرد.

مشکل تابع فعالسازی Tanh مشابه مشکل تابع سیگموئید است و زمانی که تعداد لایه‌های پنهان شبکه عصبی زیاد باشند، در یادگیری شبکه عصبی و مرحله انتشار رو به عقب، مسئله محوشدگی گرادیان رخ می‌دهد.

تابع فعالسازی غیرخطی یکسوساز در شبکه های عصبی

تابع فعالسازی غیرخطی RELUs یکی از رایج‌ترین توابع فعالسازی در یادگیری عمیق و «شبکه های عصبی پیچشی» (Convolutional Neural Networks | CNN) محسوب می‌شود. نام این تابع مخفف عبارت «Rectified Linear Unit» به معنای «واحد خطی اصلاح شده» است.

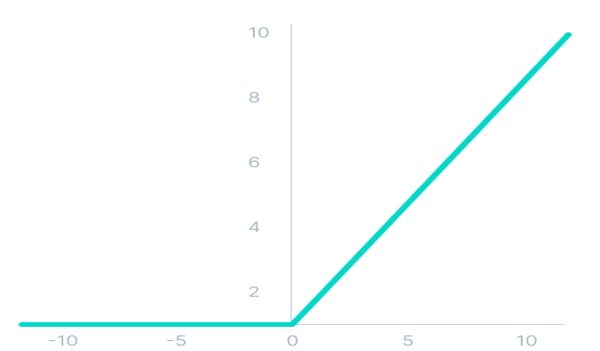
اگرچه این تابع، ظاهری شبیه به تابع خطی دارد، اما این تابع مشتق‌پذیر است و از آن می‌توان در مرحله انتشار رو به عقب استفاده کرد. این تابع تمامی گره‌ها را همزمان فعال نمی‌کند. به عبارتی، گره‌ها زمانی غیرفعال هستند که مقدار ورودی این تابع کمتر از صفر باشد. به عبارتی، براساس نمودار این تابع، چنانچه ورودی تابع بزرگتر از صفر باشد، خروجی تابع برابر با ورودی تابع و اگر ورودی تابع، مقداری کم‌تر از صفر باشد، خروجی تابع برابر با صفر است. تابع RELUs و مشتق آن یکنواخت هستند.

مزایای تابع فعالسازی RELUs به شرح زیر است:

• تابع RELUs تابعی مشتق‌پذیر است.
• به دلیل ویژگی خطی بودن و «غیراشباع‌کنندگی» (non-saturating) تابع، همگرایی الگوریتم «گرادیان کاهشی» (Gradient Descent‌) سریع‌تر اتفاق می‌افتد. بدین ترتیب، مدل به زمان کمتری برای یادگیری نیاز دارد.
• از آنجا که این تابع فقط تعدادی از گره‌ها را فعال می‌کند، به لحاظ محاسباتی از کارایی بهتری نسبت به سایر توابع فعالسازی در شبکه های عصبی برخوردار است.
• این تابع در مقایسه با توابع سیگموئید و Tanh، تابعی ساده‌تر است و بنابراین محاسبات ریاضیاتی ساده‌تری در طی یادگیری شبکه انجام می‌شود.
• تابع RELUs مشکل محوشدگی گرادیان توابع سیگموئید و Tanh را ندارد؛ زیرا محدوده مثبت خطی این تابع به گرادیان‌ها اجازه می‌دهد در مسیر فعال گره‌ها در جریان باشند. همچنین، این تابع محدودیتی برای ماکسیمم مقدار ورودی ایجاد نمی‌کند.

محدودیت مهمی که تابع RELUs با آن مواجه می‌شود، مسئله «زوال» (Dying) تابع RELUs است. این حالت زمانی اتفاق می‌افتد که خروجی چندین تابع RELUs به صورت متوالی برابر با صفر باشد. با توجه به بخش قرمز رنگ تصویر زیر، مسئله زوال تابع RELUs زمانی رخ می‌دهد که ورودی این تابع مقادیر منفی باشند.

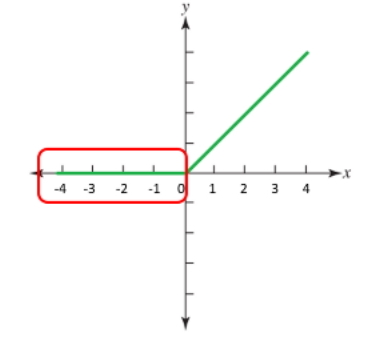
با اینکه ویژگی تابع RELUs (یعنی نادیده گرفتن مقادیر منفی ورودی) باعث عملکرد بهتر شبکه در یادگیری می‌شود، زمانی که بیشتر ورودی‌های توابع RELUs در بازه منفی باشند، مشکل زوال را به وجود می‌آورند. در حالتی که اکثر خروجی‌های توابع برابر با صفر شوند، در مرحله انتشار رو به عقب، گرادیان‌ها در طول شبکه جریان پیدا نمی‌کنند و به این ترتیب، وزن‌های شبکه به‌روزرسانی نمی‌شوند. بنابراین، در این حالت، بخش بزرگی از شبکه عصبی غیرفعال باقی می‌ماند و یادگیری شبکه به‌درستی انجام نمی‌شود.

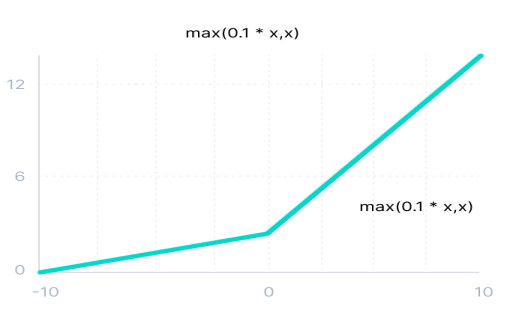
تابع فعالسازی یکسوساز Leaky در شبکه های عصبی

این تابع فعالسازی، نسخه بهبودیافته از تابع فعالسازی یکسوساز RELUs است که مشکل زوال تابع RELUs را حل می‌کند. در تابع Leaky RELUs، برای ناحیه منفی، شیب ملایم مثبتی درنظر گرفته می‌شود.

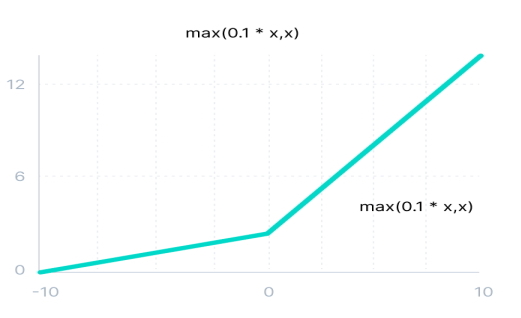
رابطه ریاضی تابع فعالساز Leaky RELUs به صورت زیر است:

\[
f(x) = max(0.1x, x)
\]

مزایای تابع فعالسازی Leaky RELUs مشابه مزایای تابع فعالسازی RELUs هستند، با این تفاوت که این تابع مشکل زوال تابع RELUs را برای مقادیر ورودی منفی ندارد و مشکلی برای مرحله انتشار رو به عقب به وجود نمی‌آورد. با درنظر گرفتن شیب ملایمی برای مقادیر منفی ورودی، گرادیان سمت چپ نمودار صفر نمی‌شود. به این ترتیب، گره‌های شبکه عصبی غیرفعال نخواهند شد.

معایب تابع Leaky RELUs به شرح زیر است:

• پیش‌بینی تابع برای مقادیر ورودی منفی ثابت است.
• مقدار گرادیان برای مقادیر منفی ورودی بسیار کوچک است. این مسئله باعث می‌شود یادگیری شبکه عصبی زمان‌بر باشد.

تابع فعالسازی یکسوساز پارامتریک در شبکه عصبی

این تابع فعالسازی، نوع دیگری از تابع فعالسازی RELUs است. به عبارتی، تابع Parametric RELUs نیز به منظور رفع مشکل زوال تابع RELUs برای مقادیر ورودی منفی ارائه شده است. این تابع، پارامتری را با عنوان a برای شیب منحنی نمودار تابع RELUs در قسمت منفی نمودار درنظر می‌گیرد که در طی یادگیری مدل شبکه عصبی و زمان انتشار رو به عقب، مقدار این پارامتر یاد گرفته می‌شود.

تابع ریاضی فعالساز Parametric RELUs به صورت زیر نوشته می‌شود که در این تابع، پارامتر a مقدار شیب را برای مقادیر ورودی منفی تابع مشخص می‌کند:

\[
f(x) = max(ax, x)
\]

تابع فعالسازی Parametric RELUs نسبت به تابع Leaky RELUs برتری دارد. به عبارتی، تابع فعالسازی Leaky RELUs با درنظر گرفتن شیب ملایم برای مقادیر منفی ورودی خود هنوز نمی‌تواند مشکل گره‌های غیرفعال را به‌طور کامل حل کند و بخشی از اطلاعات مهم ورودی در طول شبکه از دست می‌رود.

تنها مشکل تابع فعالسازی Parametric RELUs این است که براساس مقادیر مختلف پارامتر a، این تابع عملکرد متفاوتی در مسائل مختلف دارد.

 تابع فعالسازی ELUss در شبکه عصبی

تابع فعالسازی ELUss یا تابع فعالسازی واحدهای خطی نمایی یکی از انواع تابع فعالسازی RELUs به حساب می‌آید که برای مقادیر ورودی منفی تابع، شیبی درنظر می‌گیرد. در توابع فعالسازی Leaky RELUs و Parametric RELUs نمودار توابع در ناحیه منفی، به‌صورت خط مستقیم است. تابع فعالسازی ELUs، برای این ناحیه، منحنی لگاریتمی به شکل زیر تعریف می‌کند.

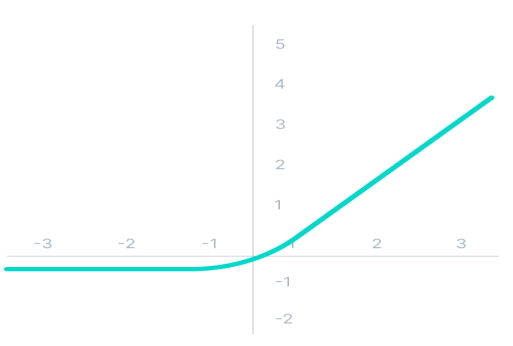
تابع ریاضی فعالساز ELUs به صورت زیر نوشته می‌شود:

$$f(x)\colon \biggl\{\begin{array}{@{}r@{\;}l@{}}x& for & x\geq0\\\alpha(e^x-1) & for &x<0\end{array}$$

مزیت‌های تابع فعالسازی ELUs نسبت به سایر توابع RELUs به شرح زیر است:

• شیب منحنی تابع ELUs بسیار ملایم است و این ویژگی تا رسیدن به مقدار $$- \alpha$$ ادامه‌دار است. در تابع فعالسازی RELUs چنین شیب ملایمی دیده نمی‌شود.
• این تابع، با درنظر گرفتن منحنی لگاریتمی برای مقادیر ورودی منفی، مانع بروز زوال تابع می‌شود. همچنین، این ویژگی باعث می‌شود مقادیر وزن‌ها و بایاس به‌درستی یاد گرفته شوند.

محدودیت‌های تابع فعالسازی ELUs به شرح زیر است:

• به دلیل انجام محاسبات نمایی، زمان محاسبات بیشتر می‌شود.
• در تابع ELUs‌، پارامتری (مشابه با پارامتر a در تابع Parametric RELUs) وجود ندارد که در حین یادگیری شبکه عصبی، مقدار آن نیز یاد گرفته شود.
• در هنگام استفاده از این تابع ممکن است مشکل انفجار گرادیان رخ دهد.

 تابع فعالسازی Softmax در شبکه عصبی

پیش از آنکه به ورودی و خروجی تابع فعالسازی Softmax پرداخته شود، به تابع سیگموئید اشاره کوتاهی می‌شود که ایده طراحی تابع Softmax از این تابع گرفته شده است. همان‌طور که بیان شد، براساس خروجی تابع سیگموید که بین بازه 0 تا 1 است، از این تابع برای محاسبه احتمال استفاده می‌شود.

 

با این حال، تابع فعالسازی سیگموئید یک مشکل اساسی دارد. چنانچه چندین خروجی به صورت 0.8، 0.9، 0.6، 0.7  و 0.8 تولید شوند، جمع تمامی خروجی‌ها بیشتر از عدد 1 می‌شود؛ در حالی که جمع مقادیر احتمالاتی باید عدد 1 باشد.

تابع ریاضی فعالساز Softmax به صورت زیر است:

\[
Softmax(z_{i}) = \frac{exp(z_{i})}{\Sigma_{j} exp(z_{j})}
\]

تابع فعالسازی Softmax نوعی از تابع سیگموئید به حساب می‌آید. به عبارتی، تابع Softmax ترکیبی از چندین تابع سیگموئید است که احتمالات نسبی را محاسبه می‌کند. به عبارتی، تابع Softmax احتمالات چندین کلاس را مشخص می‌کند.

معمولاً، در تسک‌های «دسته‌بندی چند-کلاسه» (Multi-Class Classification)، از تابع فعالسازی Softmax در لایه آخر شبکه عصبی استفاده می‌شود.

تابع فعالسازی Swish در شبکه عصبی

این تابع فعاسازی را محققان گوگل ارائه کرده‌اند و به لحاظ کارآیی، عملکرد بهتری نسبت به تابع فعالسازی RELUs در شبکه های عمیق دارد. از تابع فعالسازی Swish در مسائلی نظیر «دسته‌بندی تصاویر» (Image Classification) و ترجمه ماشین استفاده می‌شود.

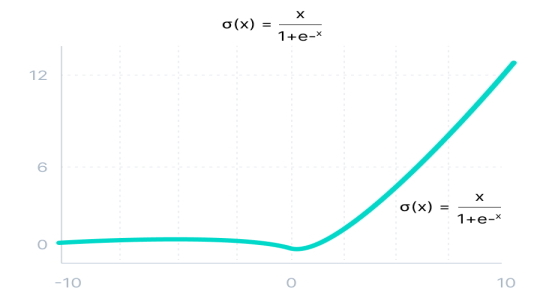
در این تابع، زمانی که مقدار x به سمت منفی بی‌نهایت میل می‌کند، مقدار y به سمت مقداری ثابت نزدیک می‌شود. با میل کردن مقدار x به مقدار مثبت بی‌نهایت، مقدار y نیز به سمت مثبت بی‌نهایت میل می‌کند.

تابع ریاضی فعالساز Swish به صورت زیر است:

$$f(x) = x*sigmoid(x)$$

مزیت‌های تابع فعالسازی Swish در شبکه عصبی در زیر فهرست شده‌اند:

• تابع Swish، تابعی پیوسته و مشتق‌پذیر است.
• شیب منحنی تابع Swish ملایم است و مانند تابع فعالسازی RELUs (زمانی که مقدار x نزدیک به صفر است) به یکباره تغییر جهت نمی‌دهد. به عبارتی، منحنی این تابع به آرامی از مقدار 0 به مقدار کوچک‌تر از 0 و پس از آن به مقادیر بیشتر از 0 تغییر جهت می‌دهد.
• در تابع فعالسازی RELUs، مقادیر منفی، به عدد 0 تبدیل می‌شدند؛ در حالی که این مقادیر منفی ممکن است شامل اطلاعات مهمی از الگوهای داده‌ها باشند. در تابع Swish به دلیل مسئله «پراکندگی» (Sparsity)، فقط مقادیر منفی بزرگ به مقدار صفر تبدیل می‌شوند.
• تابع Swish، تابعی «غیریکنواخت» (non-monotonous) است که همین مسئله به یادگیری وزن‌های شبکه کمک می‌کند.
• مسئله زوال تابع فعالسازی RELUs در تابع Swish اتفاق نمی‌افتد.

معایبی که تابع فعالسازی Swish دارد، به شرح زیر است:

• تابع Swish در محاسبات خود از تابع سیگموئید استفاده می‌کند. به همین دلیل، محاسبات این تابع، نسبت به توابع فعالسازی RELUs سنگین‌تر است.
• براساس بررسی‌های انجام شده، عملکرد این تابع ناپایدار است و نمی‌توان از قبل خروجی آن را پیشبینی کرد.

تابع فعالسازی GELUs در شبکه عصبی

عملکرد تابع فعالسازی Gaussian Error Linear Unit یا به اختصار GELUs، با مدل‌های برتر حوزه «پردازش زبان طبیعی» (Natural Language Processing (NLP)) نظیر مدل‌های Bert ،ROBERTa ،ALBERT سازگاری دارد. این تابع فعالسازی، از ویژگی‌های تابع RELUs و روش‌های «تنظیم» (Regularization) مدل نظیر «حذف تصادفی» (dropout) و «حفظ مقادیر» (Zoneout) بهره گرفته است.

نقش تابع RELUs و عمل حذف تصادفی، مشخص کردن مقدار خروجی گره است. به عبارتی، تابع RELUs براساس مقدار ورودی، ورودی را در عدد 0 یا 1 ضرب می‌کند و در روند عمل حذف تصادفی، مقادیر ورودی‌ها به‌صورت تصادفی در عدد 0 ضرب می‌شوند. تنظیم‌کننده مدل شبکه عصبی بازگشتی نیز مقادیر ورودی را به‌صورت تصادفی در عدد 1 ضرب می‌کند تا این مقادیر، در خروجی حفظ شوند.

در تابع فعالسازی GELUs، این سه عملیات با یکدیگر ترکیب می‌شوند. به عبارتی، در ابتدا به‌صورت تصادفی مقادیر ورودی در اعداد 0 و 1 ضرب می‌شوند و درنهایت مقادیر حاصل به تابع GELUs ارسال می‌شوند تا خروجی تابع را محاسبه کند.

معادله ریاضی تابع فعالسازی GELUs به‌صورت زیر است:

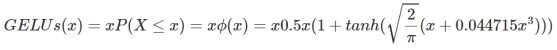
ورودی گره‌ها بعد از روند «نرمالسازی دسته» (Batch Normalization) از توزیع نرمال پیروی می‌کنند. ورودی x در مقدار m ضرب می‌شود که m برابر با \[m \sim Bernoulli(\phi(x))\] است.

مزایای تابع فعالسازی GELUs به شرح زیر است:

• در مدل‌های اخیر یادگیری عمیق، به خصوص در حوزه NLP، این تابع در مقایسه با توابع دیگر بهترین عملکرد را داشته است.
• تابع فعالسازی GELUs از مسئله محوشدگی گرادیان جلوگیری می‌کند.

از آنجا که تابع فعالسازی GELUs، تابعی جدید به حساب می‌آید (با اینکه این تابع در سال 2016 ارائه شد)، عملکرد دقیق آن در تمامی مدل‌های موجود در یادگیری عمیق هنوز نامشخص است و نیاز است تا نحوه عملکرد آن در تمامی مدل‌ها بررسی شود.

تابع فعالسازی SELUs در شبکه عصبی

تابع فعالسازی SELUs  که مخفف عبارت Scaled Exponential Linear Unit است، نرمالسازی شبکه را انجام می‌دهد. به عبارتی، این تابع مقادیر میانگین و واریانس هر لایه را حفظ می‌کند.

تابع SELUs از هر دو مقادیر  ورودی مثبت و منفی برای جابجا کردن مقدار میانگین استفاده می‌کند در حالی که در توابع RELUs‌ مقادیر منفی نادیده گرفته می‌شدند. در این تابع، از گرادیان برای تنظیم مقدار واریانس استفاده می‌شود.

نمایش ریاضی تابع SELUs‌ به‌صورت زیر است. مقادیر $$\lambda$$ و $$\alpha$$ مقادیری از پیش تعریف شده هستند.

\[
f(\alpha, x) = \lambda \biggl\{\begin{array}{@{}r@{\;}l@{}}
\alpha(e^x-1) & for & x<0\\
x& for & x\geq0
\end{array}
\]

مزیت اصلی تابع فعالسازی SELUs نسبت به تابع فعالسازی RELUs به شرح زیر است:

• عمل همگرایی در شبکه های عصبی ساخته شده از تابع فعالسازی SELUs سریع‌تر اتفاق می‌افتد زیرا سرعت انجام نرمالسازی داخلی، از سرعت انجام نرمالسازی خارجی بیشتر است. ‌
• مشکلات محوشدگی گرادیان و انفجار گرادیان برای شبکه های عصبی ساخته شده از تابع فعالسازی SELUs اتفاق نمی‌افتد.

از آنجا که تابع فعالسازی SELUs، تابعی جدید به حساب می‌آید، عملکرد دقیق آن در تمامی مدل‌های موجود در یادگیری عمیق نظیر مدل CNN هنوز نامشخص است و نیاز است تا نحوه عملکرد آن در تمامی مدل‌ها بررسی شود.

کدامیک از توابع فعالسازی در شبکه های عصبی برای پیاده سازی مناسب هستند ؟

به منظور انتخاب تابع فعالسازی مناسب، باید به هدف مدل انتخابی و تسک مورد نظر توجه کرد. می‌توان برای شروع کار، از تابع ‌RELUs به عنوان تابع فعالسازی شبکه عصبی خود استفاده کرد و چنانچه این تابع فعالسازی کارایی مناسب را نداشت، از توابع فعالسازی دیگر استفاده کرد.

نکاتی که باید حین استفاده از تابع فعالسازی در شبکه های عصبی مدنظر داشت، در زیر فهرست شده‌اند:

• از تابع فعالسازی RELUs صرفاً باید در لایه‌های پنهان شبکه عصبی استفاده شود.
• از توابع فعالسازی سیگموئید  و Tanh نباید در لایه‌های پنهان شبکه عصبی استفاده شود زیرا مشکل محوشدگی گرادیان رخ می‌دهد.
• از تابع فعالسازی Swish بهتر است در شبکه های عصبی با بیش از 40 لایه پنهان استفاده شود.

به منظور انتخاب مناسب‌ترین تابع فعالسازی برای لایه نهایی شبکه عصبی، باید به هدف مدل و نوع پیشبینی مدل توجه کرد. در ادامه، به انواع تسک‌های دسته‌بندی با استفاده از شبکه عصبی و توابع فعالسازی مناسب آن‌ها اشاره شده است:

• مسئله رگرسیون: تابع فعالسازی مناسب برای تسک رگرسیون، تابع فعالسازی خطی است.
• مسئله دسته‌بندی دوکلاسه: مناسب‌ترین تابع فعالسازی برای لایه آخر مدل دسته‌بند دوکلاسه، تابع فعالسازی سیگموئید | Logistic است.
• تسک دسته‌بندی چندکلاسه: از تابع فعالسازی Softmax می‌توان به عنوان تابع فعالساز در لایه آخر مدل دسته‌بند چندکلاسه استفاده کرد.
• مسئله دسته‌بندی با چند برچسب (Multilabel classification): در تسک‌هایی که برای هر ورودی، باید چندین دسته درنظر گرفت، بهترین تابع فعالساز، تابع فعالسازی سیگموئید است که می‌توان به تعداد هر کلاس، در لایه آخر مدل، از این تابع استفاده کرد.

جمع‌بندی

هدف از مقاله حاضر با عنوان «تابع فعالسازی در شبکه های عصبی»، معرفی کارکرد تابع فعالسازی در شبکه های عصبی بود. به منظور توضیح عملکرد توابع فعالسازی، به ارائه مفاهیم مهم و مرتبط با این توابع نظیر اصطلاحات انتشار رو به عقب، مرحله پیش‌خور، محوشدگی گرادیان و انفجار گرادیان نیز پرداخته شد.

همچنین، در این مقاله، به انواع توابع فعالسازی در شبکه های عصبی اشاره شد و مزایا و معایب هر یک از توابع فعالسازی و ویژگی‌های آن‌ها مورد مقایسه قرار گرفت. علاه‌براین، در این مقاله، به این مسئله پرداخته شد که چگونه می‌توان مناسب‌ترین تابع فعالسازی را برای شبکه عصبی خود انتخاب کرد.