انرژی خازن – به زبان ساده

در اکثر سریال‌ها یا فیلم‌هایی که در محیط بیمارستان رخ می‌دهند و یا حتی در زندگی واقعی خود احتمالاً شاهد صحنه‌های درامی بوده‌اید که طی آن پرسنل پزشکی با استفاده از یک دفیبریلاتور یا همان دستگاه شوک سعی می‌کنند تا جریان الکتریکی را از قلب یک بیمار عبور دهند تا ضربان آن به طور طبیعی شود و زنده بماند. این صحنه‌های درام همه از انرژی خازن برای نجات جان یک انسان استفاده می‌کنند. معمولاً شخصی که شوک وارد می‌کند شخص دیگر را راهنمایی می‌کند که برای مثال این بار 400 ژول دستگاه شارژ شود. انرژی داده شده توسط دفیبریلاتور در یک خازن ذخیره شده و می‌تواند متناسب با شرایط تنظیم شود، در این فرآیند معمولاً واحدهای SI به کار می‌روند.

کاربردهای دیگر خازن که بار دراماتیک کمتری دارند استفاده از خازن در میکروالکترونیک مانند ماشین حساب‌های دستی خاص برای تأمین انرژی هنگام شارژ باتری هستند. از خازن‌ها برای تأمین انرژی لامپ‌های فلاش در دوربین‌ها نیز استفاده می‌شود. در این مطلب قصد داریم انرژی خازن را مورد بررسی قرار دهیم.

انرژی خازن

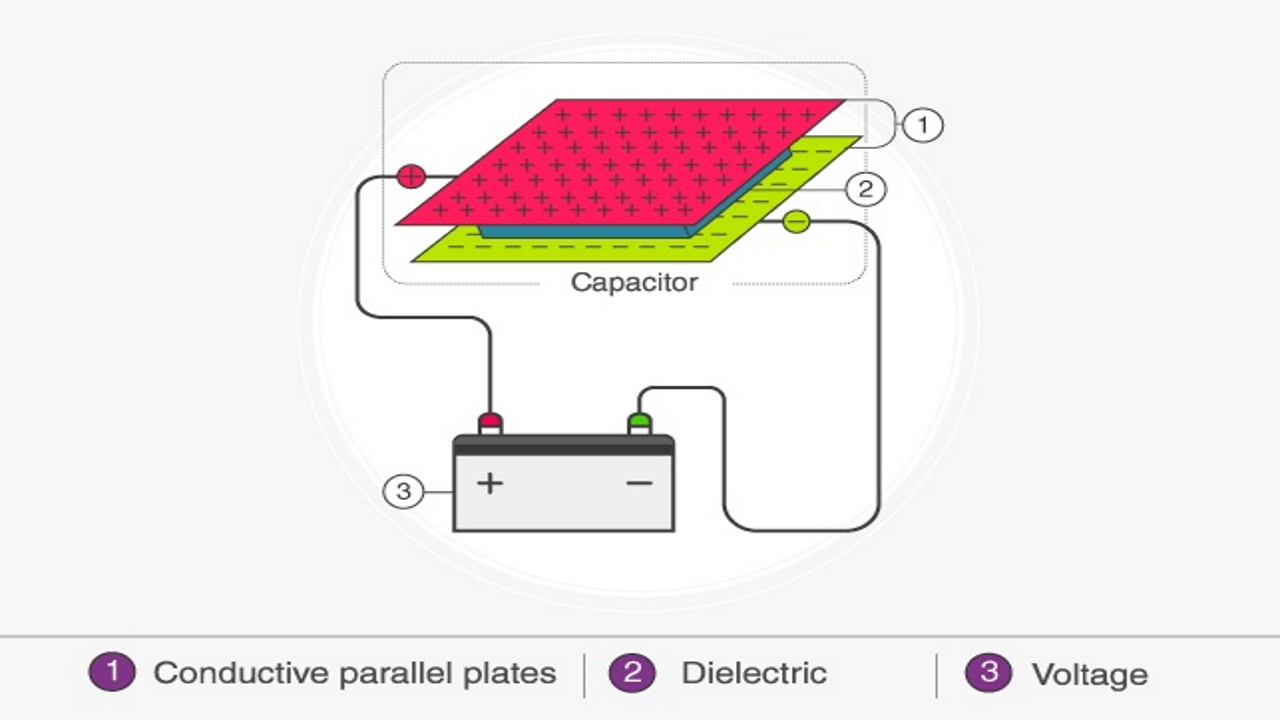
انرژی خازن از نوع انرژی پتانسیل الکتریکی است که در یک خازن ذخیره می‌شود و بنابراین به بار $$Q$$ و ولتاژ $$V$$ خازن مرتبط است. هنگام استفاده از معادله انرژی پتانسیل الکتریکی یعنی $$\Delta PE=q\Delta V$$ به یک خازن باید مراقب بود، زیرا $$\Delta PE$$ انرژی پتانسیل بار الکتریکی $$q$$ است که از طریق ولتاژ $$\Delta V$$ عبور می‌کند. اما در خازن ولتاژ در ابتدا صفر است و با باردار شدن تدریجی خازن ولتاژ آن افزایش می‌یابد.

اولین بار قرار داده شده روی خازن تغییر ولتاژ $$\Delta V=0$$ را تجربه می‌کند، زیرا خازن در ابتدا هنگام شارژ شدن ولتاژ صفر دارد. بار نهایی که روی خازن قرار می‌گیرد ولتاژ $$\Delta V=V$$ را تجربه می‌کند زیرا خازن اکنون ولتاژ کامل یعنی $$V$$ را در خود دارد. ولتاژ متوسط خازن در طول فرایند باردار شدن برابر با $$\frac{V}{2}$$ است و بنابراین ولتاژ متوسطی که توسط بار $$q$$ تجربه می‌شود نیز برابر با $$\frac{V}{2}$$ است. بر همین اساس انرژی ذخیره شده در خازن را که با $$E_{cap}$$ نمایش می‌دهیم برابر است با:

$$E_{cap}=\frac{QV}{2}$$

که $$Q$$ بار خازن در زمانی است که ولتاژ $$V$$ را بر آن اعمال می‌کنیم. دقت داشته باشید که در این شرایط انرژی برابر با $$\frac{QV}{2}$$ است و $$QV$$ نیست.

از طرف دیگر می‌دانیم ظرفیت خازن توسط رابطه $$C=QV$$ به بار الکتریکی و ولتاژ مرتبط است و بدین ترتیب رابطه انرژی خازن از لحاظ ریاضی می‌تواند به سه صورت زیر نوشته شود:

$$E_{cap}=\frac{QV}{2}=\frac{CV^{2}}{2}=\frac{Q^{2}}{2C}$$

که در آن $$Q$$ بار الکتریکی و $$V$$ ولتاژ و $$C$$ ظرفیت خازن است. انرژی بر حسب ژول، بار الکتریکی بر حسب کولن، ولتاژ بر حسب ولت و ظرفیت بر حسب فارادی است.

در یک دفیبریلاتور انتقال زیاد بار الکتریکی در یک شوک کوتاه به صفحه‌های دستگاه و از طریق سینه فرد می‌تواند نجات دهنده جان فرد باشد. حمله قلبی در یک فرد ممکن است از زمان شروع ضربان سریع و نامنظم قلب فیبریلاسیون قلبی یا بطنی رخ دهد. استفاده از یک شوک الکتریکی با انرژی الکتریکی زیاد می‌تواند آریتمی را خاتمه دهد و به ضربان ساز بدن اجازه دهد تا الگوهای طبیعی خود را از سر بگیرد. امروزه حمل و قرار دادن یک دفیبریلاتور برای آمبولانس‌ها امری عادی و ضروری است که از الکتروکاردیوگرام یا نوار قلب برای تجزیه و تحلیل الگوی ضربان قلب بیمار نیز استفاده می‌شود. ناگفته نماند که در دنیای کنونی دفیبریلاتورهای خارجی و خودکار (AED) در بسیاری از مکان‌های عمومی یافت می‌شوند.

این‌ دستگاه‌ها برای استفاده توسط افراد غیر متخصص طراحی شده‌اند، به طور خودکار وضعیت قلب بیمار را تشخیص می‌دهند و سپس شوک را با انرژی و شکل موج مناسب اعمال می‌کنند. CPR در بسیاری از موارد قبل از استفاده از AED (دستگاه‌های سبک و قابل حمل که با باتری کار می‌کنند. این دستگاه‌ها پدهای دارای سنسورهایی هستند که به آن‌ها الکترود گفته می‌شود) توصیه می‌شود.

مثال: یک دفیبریلاتور قلب انرژی $$4\times 10^{2}$$ ژول را با تخلیه خازنی با ولتاژ $$1\times 10^{4}$$ منتقل می‌کند، ظرفیت این خازن چقدر است؟

پاسخ: به ما $$E_{cap}$$ و $$V$$ داده شده و از ما خواسته شده تا ظرفیت $$C$$ را پیدا کنیم. از سه عبارت موجود در معادله $$E_{cap}$$ راحتترین رابطه برای مسئله این است که از رابطه $$E_{cap}=\frac{CV^{2}}{2}$$ استفاده کنیم. با حل این معادله بر حسب ظرفیت خازن یا $$C$$ داریم:

$$C=\frac{2E_{cap}}{V^{2}}$$

با قرار دادن مقادیر داده شده در معادله خواهیم داشت:

$$C=\frac{2E_{cap}}{V^{2}}=\frac{2(4\times 10^{2}\ J)}{(1\times 10^{4}\ V)^{2}}=8\times 10^{-6}\ F=8\ \mu F$$

محاسبه انرژی در خازن با استفاده از بیان کار

اگر ظرفیت یک رسانا $$C$$ باشد در ابتدا بدون بار است و اختلاف پتانسیل صفحات آن هنگام اتصال به باتری $$V$$ است. اگر در این مدت بار الکتریکی $$q$$ روی صفحات خازن ذخیره شود، مقدار این بار الکتریکی برابر است با

$$q=CV$$

از طرفی می‌دانیم کار الکتریکی برابر با $$W=Vq$$ است، یعنی کار برابر با حاصلضرب پتانسیل در بار الکتریکی است. در نتیجه اگر باتری مقدار بار بسیار کوچک $$dq$$ را در ولتاژ ثابت $$V$$ به خازن منتقل کند، کار انجام شده در این انتقال به خازن برابر است با:

$$dW=Vdq=\frac{q}{C}dq$$

بدین ترتیب کار انجام شده برای انتقال بار $$q$$ به خازن به صورت زیر به دست می‌آید:

$$W=\int_0^q\frac{q}{C}dq=\frac{1}{C}[\frac{q^{2}}{2}]_0^q=\frac{1}{2}\frac{q^{2}}{C}$$

با توجه به رابطه بین کار و انرژی پتانسیل، مقدار انرژی ذخیره شده در خازن برابر با مقدار کار انجام شده روی سیستم و برابر است با:

$$U=\frac{1}{2}\frac{q^{2}}{C}$$

فرم‌های دیگر انرژی پتانسیل نیز به آسانی با استفاده از رابطه بین ظرفیت خازن، بار الکتریکی و پتانسیل قابل محاسبه است.

در انتهای این مطلب برای درک بهتر موضوع به حل چند مثال در مورد خازن الکتریکی و انرژی آن می‌پردازیم.

مثال انرژی خازن

مثال 1: یک خازن صفحه موازی پر شده از هوا دارای ظرفیت $$5.0\ pF$$ است. با استفاده از یک باتری اختلاف پتانسیل $$100$$ ولتی به صفحات خازن که $$1\ cm$$ از هم فاصله دارند اعمال می‌شود. انرژی ذخیره شده در خازن چقدر است؟ فرض کنید باتری قطع شده باشد و صفحات خازن جابه‌جا شده و $$2\ cm$$ از هم فاصله بگیرند اکنون انرژی ذخیره شده در خازن چقدر است؟ مجدداً فرض کنید که باتری وصل است و صفحات دوباره جابه‌جا می‌شوند تا فاصله ‌آن‌ها به $$2\ cm$$ برسد. در این حالت انرژی ذخیره شده در خازن چقدر است؟

پاسخ: در حالت اول انرژی ذخیره شده در خازن به راحتی و با استفاده از رابطه $$U=\frac{1}{2}CV^{2}$$ به دست می‌آید و داریم:

$$U=\frac{1}{2}CV^{2}=\frac{(5\times 10^{-12})(100)^{2}}{2}=2.5\times 10^{-8}\ J$$

در حالت دوم زمانی که فاصله بین صفحات را افزایش می‌دهیم، ظرفیت خازن کاهش می‌یابد و از آنجا که رابطه ظرفیت برای خازن‌های صفحه موازی برابر با $$C=\frac{\epsilon_{0}A}{d}$$ است با دو برابر شدن فاصله صفحات ظرفیت خازن نصف و برابر با $$2.5\ pF$$ می‌شود. با قطع کردن باتری از خازن یعنی بار خازن ثابت است و ولتاژ تغییر می‌کند. در نتیجه داریم:

$$U=\frac{Q^{2}}{2C}$$

بار خازن نسبت به حالت قبل ثابت است و ظرفیت خازن یا مخرج رابطه بالا نصف شده است. در نتیجه انرژی ذخیره شده در خازن نسبت به حالت قبل دو برابر می‌شود و برابر با $$5\times 10^{-8}\ J$$ به دست می‌آید.

در حالت آخر اگر باطری متصل بماند و فاصله صفحات افزایش یابد و دو برابر شود، با توجه به ثابت ماندن ولتاژ از رابطه $$U=\frac{1}{2}CV^{2}$$ استفاده می‌کنیم که چون ظرفیت خازن نصف شده است، انرژی ذخیره شده نیز کاهش یافته و برابر با $$5\times 10^{-8}\ J$$ می‌شود.

مثال 2: انرژی ذخیره در مجموعه خازن‌های شکل زیر را هنگامی که خازن‌ها کاملاً شارژ شده‌اند و ظرفیت آن‌ها برابر با $$C_{1}=12\ \mu F$$، $$C_{2}=2\ \mu F$$ و $$C_{3}=4\ \mu F$$ است، محاسبه کنید.

فیلم آموزش فیزیک ۲ دانشگاه – جامع و با نکات کاربردی در فرادرس

کلیک کنید

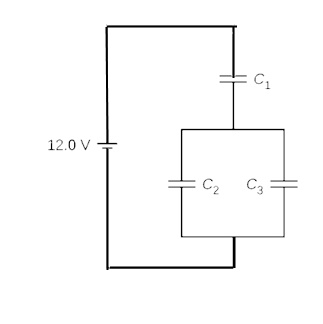
پاسخ: با استفاده از رابطه انرژی خازن یعنی $$U_{C}=\frac{1}{2}CV^{2}=\frac{1}{2}\frac{Q^{2}}{C}=\frac{1}{2}QV$$، می‌توانیم انرژی ذخیره شده در هر خازن یعنی $$U_{2}$$، $$U_{1}$$ و $$U_{3}$$ را به دست آوریم. با توجه به این که خازن‌ها به منبع ولتاژ وصل هستند یعنی باید از رابطه‌ای که بر حسب ظرفیت و ولتاژ بیان می‌شود برای محاسبه انرژی ذخیره شده خازن استفاده کنیم. برای محاسبه ولتاژ دو سر هر خازن به ترتیب زیر عمل می‌کنیم:

خازن $$C_{1}$$ به صورت سری با خازن $$C_{2}$$ و $$C_{3}$$ قرار گرفته است. دو خازن $$C_{2}$$ و $$C_{3}$$ به صورت موازی با هم قرار دارند که بدین معنی است که اختلاف پتانسیل دو سر خازن $$C_{2}$$ با خازن $$C_{3}$$ برابر است.

از طرفی $$C_{1}$$ با خازن معادل خازن $$C_{2}$$ و $$C_{3}$$ به صورت سری قرار دارد که بدین معنی است که بار الکتریکی روی خازن $$C_{1}$$ و خازن معادل 2 و 3 یا $$C_{23}$$ با یکدیگر برابر است. پس در ابتدا ظرفیت خازن معادل یا $$C_{23}$$ را به دست می‌آوریم و چون دو خازن با یکدیگر موازی هستند داریم:

$$C_{23}=C_{2}+C_{3}=2\ \mu F+4\ \mu F=6\ \mu F$$

بدین ترتیب داریم:

$$12.0 V = V_1 + V_{23} = \dfrac{Q_1}{C_1} + \dfrac{Q_{23}}{C_{23}} = \dfrac{Q_1}{12.0 \mu F} + \dfrac{Q_1}{6.0 \mu F} \Rightarrow Q_1 = 48.0 \mu C.$$

و بدین ترتیب $$V_1$$ برابر است با:

$$V_1 = \dfrac{Q_1}{C_1} = \dfrac{48.0 \mu C}{12.0 \mu F} = 4.0 V$$

و

$$V_2 = V_3 = 12.0 V - 4.0 V = 8.0 V$$

می‌شود. با به دست آمدن اختلاف پتانسیل دو سر هر خازن می‌توانیم انرژی ذخیره شده در هر خازن را به دست آوریم.

$$U_1 = \frac{1}{2}C_1V_1^2 = \frac{1}{2}(12.0 \, \mu F)(4.0 \, V)^2 = 96 \, \mu J$$

$$U_2 = \frac{1}{2}C_2V_2^2 = \frac{1}{2}(2.0 \, \mu F)(8.0 \, V)^2 = 64 \, \mu J$$

$$U_3 = \frac{1}{2}C_3V_3^2 = \frac{1}{2}(4.0 \, \mu F)(8.0 \, V)^2 = 130 \, \mu J$$

و انرژی کل ذخیره شده در این مدار برابر است با:

$$U_C = U_1 + U_2 + U_3 = 96 \, \mu J + 64 \, \mu J + 130 \, \mu J = 0.29 \, mJ$$

بدین ترتیب می‌توان انرژی ذخیره شده در یک خازن یا برای دسته‌ای از خازن‌ها را در یک مدار محاسبه کرد. نکته‌ای که در انتها باید به آن اشاره شود این است که اگر ظرفیت خازن معادل این سه خازن را به دست آورده و در مجذور ولتاژ دو سر باطری ضرب کنیم، باید به نتیجه‌ای یکسان برسیم. بدین ترتیب خواهیم داشت:

$$\dfrac{1}{C} =\frac{1}{C_{1}}+\frac{1}{C_{23}}= \dfrac{1}{12.0 \mu F} + \dfrac{1}{6.0 \mu F} = \dfrac{1}{4.0 \mu F} \Rightarrow C = 4.0 \mu F$$

و انرژی ذخیره شده در خازن برابر است با:

$$U_C = \frac{1}{2}CV^2 = \frac{1}{2}(4.0 \, \mu F)(12.0 \, V)^2 = 0.29 \, mJ$$

که با نتیجه به دست آمده در قسمت قبل تطابق دارد.

جمع‌بندی

در این مطلب انرژی خازن را بررسی و رابطه آن را بیان کردیم. همچنین این مطلب را با استفاده از بیان کار نیز مورد مطالعه قرار دادیم. در انتهای این بحث نیز با حل چند مثال سعی کردیم درک موضوع را در ذهن خواننده آسان‌تر کنیم.