انرژی آزاد هلمهولتز – به زبان ساده

در علم ترمودینامک، انرژی آزاد هلمهولتز یک پتانسیل ترمودینامیکی است که کار مفید را در یک سیستم بسته ترمودینامیکی در شرایط همدما و هم‌حجم اندازه‌گیری می‌کند. در صورتیکه حجم ثابت نباشد، بخشی از کار انجام شده را به عنوان «کار مرزی» (Boundary Work) در نظر می‌گیرند. در نتیجه، در سیستم‌هایی با حجم ثابت، استفاده از انرژی هلمهولتز بسیار مفید خواهد بود. علاوه بر این، در دمای ثابت، انرژی آزاد هلمهولتز در حالت تعادل، کمترین مقدار خود را خواهد داشت.

در مقابل، انرژی آزاد گیبس یا آنتالپی آزاد،‌ به طور معمول به عنوان معیاری از اندازه‌گیری پتانسیل ترمودینامیکی در شرایط فشار ثابت در نظر گرفته می‌شود. به طور مثال، به هنگام بررسی واکنش‌های انفجاری، از انرژی آزاد هلمهولتز بهره می‌گیرند چراکه به طور معمول این نوع از واکنش‌ها موجب تغییرات فشار می‌شوند. انرژی آزاد هلمهولتز همچنین بمنظور تعریف اساسی معادله حالت مواد خالص مورد استفاده قرار می‌گیرد.

مفهوم انرژی آزاد توسط دانشمند آلمانی، «هرمان فون هلمهولتز» (Hermann von Helmholtz) برای اولین بار در سال 1882 معرفی شد. آیوپاک برای این مفهوم،‌ نماد $$A$$ و نام انرژی هلمهولتز را در نظر گرفته است. در علم فیزیک، از نماد $$F$$ برای ارجاع به انرژی آزاد یا تابع هلمولتز استفاده می‌کنند.

تعریف انرژی آزاد هلمهولتز

انرژی هلمهولتز را به صورت رابطه زیر تعریف می‌کنند:

$${\displaystyle F \equiv U - T S}$$

• $$F$$: انرژی آزاد هلمهولتز که آن را با $$A$$ نیز نشان می‌دهند و واحد آن در SI، ژول است.
• $$U$$: انرژی داخلی سیستم با واحد ژول
• $$T$$: دمای محیط اطراف با واحد کلوین که این دما را با «حمام گرمایی» (Heat Bath)، مدلسازی می‌کنند.
• $$S$$: آنتروپی سیستم با واحد ژول در SI

بیان ترمودینامیکی انرژی آزاد هلمهولتز

بر اساس قانون اول ترمودینامیک در یک سیستم بسته، رابطه زیر برقرار است:

$${\displaystyle \mathrm {d} U =\delta Q \ +\delta W }$$

فیلم آموزش شیمی فیزیک – حل مساله + گواهینامه در فرادرس

کلیک کنید

در این رابطه، $$\delta Q$$، انرژی اضافه شده به سیستم به صورت گرما و $$\delta W$$، کار انجام شده بر روی سیستم است. قانون دوم ترمودینامیک برای یک واکنش برگشت‌پذیر نیز به صورت زیر تعریف می‌شود:

$${\displaystyle \delta Q = T\,\mathrm {d} S}$$

در صورتیکه یک تغییر برگشت‌پذیر داشته باشیم، کار انجام شده را می‌توان با رابطه $${\displaystyle \delta W = -p\,\mathrm {d} V}$$ توصیف کرد و در نتیجه، قانون اول ترمودینامیک را می‌توان به صورت زیر نشان داد:

$${\displaystyle \mathrm {d} U = T\,\mathrm {d} S - p\,\mathrm {d} V}$$

با اعمال قانون ضرب در مشتق $$(d(T S) = T d S + S d T)$$ به رابطه زیر خواهیم رسید:

$${\displaystyle \mathrm {d} (U - T S) = - S\,\mathrm {d} T -p\,\mathrm {d} V}$$

از تعریفی که در بخش قبل برای انرژی آزاد هلمهولتز بیان کردیم استفاده می‌کنیم و به رابطه زیر می‌رسیم:

$${\displaystyle \mathrm {d} F = - S\,\mathrm {d} T - p\,\mathrm {d} V}$$

از آن‌جایی که عبارت $$F$$ یک تابع حالت ترمودینامیکی است، این رابطه تا زمانی که فشار و دما در سیستم ثابت باشند، در فرآیندهای غیر برگشت‌پذیر نیز صدق می‌کند.

در تعریفی دیگر،‌ انرژی هلمهولتز را می‌توان با مراحل زیر توصیف کرد. در تعاریف بالا، قانون اول ترمودینامیک را به صورت زیر تعریف کردیم:

$$d U = T d S - P d V$$

این عبارت، تنها در تغییرات برگشت‌پذیر صحت دارد. اگر فشار را ثابت فرض کنیم، عبارت $$- P d V$$ حذف خواهد شد. با توجه به نامساوی کلازیوس $$(d S > \dfrac{δ q}{ T })$$ در حجم ثابت خواهیم داشت:

$$\underset{ \text{} }{dU \le TdS }$$

$$\underset{ \text{} }{ dU-TdS \le 0 }$$

با توجه به تعریف انرژی هلمهولتز، داریم:

$$\begin{equation} \begin{array}{c} {A \equiv U - T S} \\ {d A = d U - T d S - S d T} \end{array} \end{equation}$$

اگر در این رابطه، دما را هم ثابت فرض کنیم، به رابطه زیر (در دما و فشار ثابت) می‌رسیم:

$$\underset{ \text{} }{ dA=dU-TdS \le 0 }$$

این رابطه بیان می‌کند که در فرآیندهای خود‌به‌خودی، مقدار انرژی هلمهولتز به صورت کاهشی است.

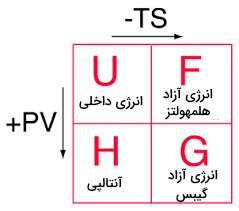
اصل انرژی حداقل و کار حداکثر

قوانین ترمودینامیک را به راحتی در سیستم‌هایی تحت فرآیندهای برگشت‌پذیر یا فرآیندهایی با آغاز و اختتام در تعادل حرارتی، می‌توان بکار گرفت. همچنین، «فرآیندهای شبه‌استاتیک برگشت‌ناپذیر» (Irreversible Quasistatic Processes) یا فرآیندهایی خودبه‌خودی با دما و فشار ثابت نیز قابل بررسی هستند. این بررسی بر اساس روابط اساسی در ترمودینامیک انجام می‌شود که در ادامه به آن خواهیم پرداخت.

در ابتدا اگر بخواهیم پدیده‌ای همچون واکنش‌های شیمیایی را مورد بررسی قرار دهیم بهتر است تا حالت‌های مناسب اولیه و نهایی یک سیستم را در تعادل حرارتی در نظر بگیریم. اگر سیستم را در حجم ثابت و در تماس با یک حمام گرمایی (با دمای ثابت) قرار دهیم، در آن‌صورت می‌توانیم به توصیف این پدیده بپردازیم.

از آن‌جایی که متغیرهای ترمودینامیکی سیستم را به خوبی در حالت‌های اولیه و نهایی تعریف کرده‌ایم، انرژی داخلی،‌ آنتروپی و کار نیز به درستی تعریف خواهند شد. با استفاده از قانون پایستگی انرژی خواهیم داشت:

$${\displaystyle \Delta U _ {\text{bath}}+\Delta U + W = 0}$$

حجم سیستم ثابت نگهداشته شده است، این بدان معنی است که حجم حمام گرمایی نیز تغییر نمی‌کند و نتیجه می‌گیریم که حمام گرمایی، کاری انجام نمی‌دهد. در نتیجه، مقدار گرمای منتقل شده به حمام گرمایی به صورت زیر تعریف می‌شود:

$${\displaystyle Q _ {\text{bath}}=\Delta U _ {\text{bath}}=-(\Delta U + W)}$$

حمام گرمایی، مستقل از سیستم، در یک تعادل گرمایی در دمای T باقی خواهد ماند. در نتیجه، تغییرات آنتروپی حمام گرمایی عبارتست از:

$${\displaystyle \Delta S_{\text{bath}}={\frac {Q_{\text{bath}}}{T}}=-{\frac {\Delta U+W}{T}}}$$

بنابراین، تغییرات آنتروپی کل به صورت زیر تعریف می‌شود:

$${\displaystyle \Delta S _ {\text{bath}}+\Delta S = -{\frac {\Delta U - T\Delta S + W}{ T }}}$$

با توجه به اینکه سیستم در یک تعادل با حمام گرمایی در شرایط اولیه و نهایی قرار دارد، بنابراین، T را می‌توان به عنوان دمای سیستم در این شرایط نیز در نظر گرفت. عدم تغییر دمای سیستم سبب می‌شود تا صورت کسر را به شکل تغییر انرژی آزاد سیستم تعریف کنیم و خواهیم داشت:

$${\displaystyle \Delta S _ {\text{bath}}+\Delta S = -{\frac {\Delta F + W}{ T}}}$$

از آن‌جایی که تغییرات آنتروپی همواره مساوی یا بزرگتر از صفر است، به نامساوی زیر می‌رسیم:

$${\displaystyle W \leq - \Delta F}$$

در اینجا می‌بینیم که کل کاری از یک سیستم در فرآیند همدما بدست می‌آید، با کاهش انرژی آزاد محدود شده است و این افزایش انرژی آزاد در یک فرآیند برگشت‌پذیر، نیازمند انجام کار بر روی سیستم است. اگر هیچ کاری از سیستم حاصل نشود، مقدار آن صفر خواهد بود و به نامساوی زیر خواهیم رسید:

$${\displaystyle \Delta F \leq 0}$$

در نتیجه، برای یک سیستم در دما و حجم ثابت که نتواند کار الکتریکی یا کاری به غیر از $$PV$$ انجام دهد،‌ انرژی آزاد کل در طول یک تغییر خودبه‌خودی، همانطور که در بالا نیز به آن اشاره شد، کاهشی خواهد بود. این نتیجه گویی با رابطه $$dF = −S dT − P dV$$ در تضاد است چراکه با ثابت نگاه‌داشتن دما و حجم، $$d F = 0$$ و در نتیجه، $$F$$ مقداری ثابت خواهد داشت. در واقعیت چنین تضادی وجود ندارد. در یک سیستم تک‌جزئی، که رابطه $$dF = −S dT − P dV$$ محدود می‌شود، هیچ فرآیندی در دما و حجم ثابت قابل انجام نیست.

برای اینکه فرآیندی در دما و حجم ثابت به طور خود به خودی انجام شود، باید حالت ترمودینامیکی فضای سیستم بزرگ‌تر شود. در خصوص یک واکنش شیمیایی، این بدان معنی است که تعداد ذرات j $$(N_j)$$ تغییر پیدا کند و در نتیجه، شکل دیفرانسیلی انرژی آزاد به صورت زیر خواهد بود:

$$\begin{equation} d F=-S d T-P d V+\sum_{j} \mu_{j} d N_{j} \end{equation}$$

• $$N_j$$: تعداد ذرات نوع j
• $$\mu _ {j }$$: پتانسیل شیمیایی

در شرایطی که تغییرات خود به خودی در دما و حجم ثابت بدون کار الکتریکی داشته باشیم، مولفه آخر، منفی می‌شود. همچنین، در حالاتی که پارامترهای خارجی دیگری نیز داشته باشیم، رابطه بالا به صورت زیر تغییر پیدا می‌کند که در این رابطه، $$x_i$$، متغیرهای خارجی و $$X_i$$ متناظر با «نیروهای تعمیم یافته» (Generalized Forces) است.

$${\displaystyle d F = - S \, d T-\sum _{ i } X _{ i }\,d x_ {i }+\sum _ { j }\mu _ { j }\, d N _{ j }}$$

ارتباط انرژی آزاد هلمهولتز با سایر متغیرها

تعریفی که در ابتدا برای انرژی آزاد هلمهولتز ارائه دادیم به شکل زیر است:

$${\displaystyle F = U - T S}$$

رابطه اساسی در ترمودینامیک نیز به صورت زیر تعریف می‌شود:

$${\displaystyle d F = -S \, d T - P\, d V + \mu \,d N}$$

با ترکیب این دو معادله، روابطی برای آنتروپی، فشار و پتانسیل شیمیایی به صورت زیر بدست می‌آیند:

$${\displaystyle S = - {\bigg (}{\frac {\partial F }{\partial T }}{\bigg )}{\bigg |}_{ V , N },\quad P = - {\bigg (}{\frac {\partial F }{\partial V }}{\bigg )}{\bigg | } _ { T , N } ,\quad \mu ={\bigg (}{\frac {\partial F }{\partial N }}{\bigg )}{\bigg | } _ { T , V }}$$

همچنین به کمک مکانیک آماری و «تابع پارش» (Partition Function) خواهیم داشت:

$${\displaystyle F = - kT \log Z}$$

با استفاده از روابط بالا، راه مناسبی برای محاسبه متغیرهای ترمودینامیکی بدست می‌آید که به طور معمول در محاسبات «چگالی حالت» (Density of States) فیزیک حالت جامد مورد استفاده قرار می‌گیرد. همچنین برای سیستم‌های مختلف می‌توان از «تبدیلات لژاندر» (Legendre Transformations) بهره گرفت. به طور مثال، برای یک سیستم با میدان مغناطیسی یا پتانسیل خواهیم داشت:

$${\displaystyle m = - {\bigg (}{\frac {\partial F }{\partial B }}{\bigg )}{\bigg | } _ { T , N } , \quad V = {\bigg (}{\frac {\partial F }{\partial Q }}{\bigg )}{\bigg |} _ {N , T}}$$

شکل کلی انرژی آزاد هلمهولتز

در شکل کلی‌تر رابطه انرژی آزاد هلمهولتز باید عبارت مکانیکی $$p dV$$ را با حاصلضرب حجم، تنش و «کرنش بی‌نهایت کوچک» (Infinitesimal Strain) جایگزین کنیم:

$${\displaystyle \mathrm {d } F = V \sum _{ i j }\sigma _ {i j}\,\mathrm {d} \varepsilon _{ij}-S\,\mathrm {d} T + \sum _ { i }\mu _ { i }\,\mathrm {d } N _ { i} }$$

$$\sigma _{ij}$$ و $${\displaystyle \varepsilon _{ij}}$$ به ترتیب، «تنسور» (Tensor) تنش و کرنش هستند. در شرایط الاستیسیته خطی، برای ماده‌ای که از قانون هوک (فنر) تبعیت کند، ارتباط بین تنش و کرنش به کمک رابطه زیر امکان‌پذیر است:

$${\displaystyle \sigma _ { i j } = C _ {i j k l}\varepsilon _ {k l}}$$

با استفاده از «قانون جمع‌زنی انیشتین» (Einstein Notation) برای تنسورها، به رابطه‌ای برای محاسبه انرژی آزاد هلمهولتز می‌رسیم که به صورت زیر است:

$${\displaystyle {\begin{aligned}F & = {\frac {1}{2}}V C _ {i j k l }\varepsilon _ {i j}\varepsilon _ { k l }- S T + \sum _ { i} \mu _{i}N _ { i } \\& = {\frac {1}{ 2}}V \sigma _ { i j } \varepsilon _ { i j } - S T +\sum _{i}\mu _ { i } N _ {i }\end{aligned}}}$$

اگر این مطلب برای شما مفید بوده‌ است،‌ آموزش‌ها و مطالب زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس شیمی
• مجموعه آموزش‌های مهندسی شیمی
• آموزش ترمودینامیک مهندسی شیمی
• فوگاسیته چیست؟ — به زبان ساده
• نظریه برخورد — به زبان ساده

^^