انتقال حرارت بدن انسان – به زبان ساده

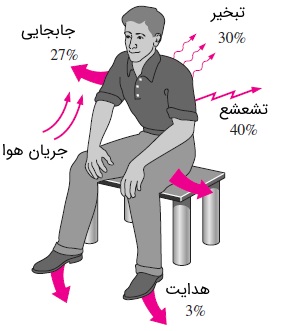
حرارت تولید شده در بدن انسان، از طریق پوست و ریهها به محیط اطراف منتقل میشود. این کار به شیوه انتقال حرارت جابجایی و تشعشع (گرمای محسوس) و همچنین با کمک تبخیر (گرمای نهان) انجام میپذیرد. گرمای نهان (Latent Heat)، نشان دهنده گرمای حاصل از تبخیر آب در ریهها و روی پوست است. تبخیر از طریق جذب حرارت بدن اتفاق میافتد. گرمای حاصل از فرو بردن هوا در ریهها، نشان از انتقال حرارت محسوس (Sensible Heat) دارد و این شیوه انتقال حرارت بدن انسان با بالا رفتن دمای ورودی به ریهها، افزایش مییابد.
معادله انتقال حرارت بدن انسان
نرخ خالص انتقال حرارت بدن انسان را میتوان با عبارت زیر نشان داد.
$$\large \dot {Q} _{\text {body, total}} \:=\: \dot {Q} _{\text {skin}} \:+\: \dot {Q} _{\text {lungs}} \\~\\
\large =\: (\dot {Q} _{\text {sensible}} \:+\: \dot {Q} _{\text {latent}}) _{\text {skin}} \:+\: (\dot{Q} _{\text {sensible}} \:+\: \dot {Q} _{\text {latent}}) _{\text {lungs}} \\~\\
\large =\: (\dot {Q} _{\text {convection}} \:+\: \dot {Q} _{\text {radiation}} \:+\: \dot{Q} _{\text {latent}}) _{\text {skin}} \:+\: (\dot {Q} _{\text {convection}} \:+\: \dot {Q} _{\text {latent}}) _{\text {lungs}}$$
همانطور که ملاحظه میکنید، آنالیز و تعیین انتقال حرارت بدن انسان کار سادهای نیست. علاوه بر این، پوشیدن لباس و ساز و کار انتقال حرارت از لابلای روزنههای آن نیز کار را دشوارتر کرده و تحلیلها را به سمت اتکا به دادههای آزمایشگاهی سوق میدهد. در شرایط پایدار، نرخ خالص انتقال حرارت بدن را میتوان با نرخ تولید حرارت متابولیک یکسان دانست. تفاوت بین این دو پارامتر، از حدود $$\large 100\:W$$ برای کارهای اداری سبک تا $$\large 1000\:W$$ در کارهای فیزیکی سنگین، متغیر است.
افت حرارت محسوس از طریق پوست، به دمای پوست، محیط، سطوح نزدیک و حتی جریان هوا وابسته است. اما در طرف مقابل، افت حرارت نهان، به خیس بودن پوست و رطوبت نسبی محیط بستگی دارد. لباس مانند عایق عمل کرده و هر دو شکل انتقال حرارت (محسوس و نهان) را کاهش میدهد. بدیهی است که انتقال حرارت از طریق ریهها در دم و بازدم نیز از فرکانس تنفس، حجم ریهها و برخی عوامل محیطی تأثیر میپذیرد.
حرارت محسوس از پوست پوشیده شده با لباس، ابتدا به لباس و سپس از لباس به محیط منتقل میشود. افت حرارت جابجایی و تشعشع از سطح بیرونی لباس به محیط بیرون را میتوان به ترتیب زیر نشان داد.
$$\large \dot{Q}_{\text {conv}} \:=\: h_{\text {conv}} A_{\text {clothing}} (T_ {\text {clothing}} \:-\: T_ {\text {ambient}}) \\~\\
\large \dot{Q}_{\text {rad}} \:=\: h_{\text {rad}} A_{\text {clothing}} (T_ {\text {clothing}} \:-\: T_ {\text {surr}})$$
در رابطههای بالا، $$\large h_{\text {conv}}$$ و $$\large h_{\text {rad}}$$ به ترتیب ضرایب انتقال حرارت جابجایی و تشعشعی را نشان میدهند. مساحت بیرونی فرد پوشیده شده با لباس برابر $$\large A_{\text {clothing}}$$ و دمای میانگین پوست و لباس برابر $$\large T_ {\text {clothing}}$$ است. ضمناً $$\large T_ {\text {surr}}$$ نیز به دمای میانگین سطوح اطراف اشاره میکند. دمای سطوح مختلفی که در نزدیکی انسان قرار دارد، با یکدیگر متفاوتند و این پارامتر، دمای متوسط تشعشع را نشان میدهد. $$\large T_ {\text {surr}}$$ عبارت است از دمای فرضی یک محفظه همدما که در آن، انتقال حرارت تشعشعی با بدن انسان و انتقال حرارت تشعشعی با محفظه با یکدیگر برابرند. با توجه به اینکه بسیاری از لباسها و ساختمانها، رنگهای تیره بیش از سایر رنگها به کار رفته، دمای متوسط تشعشع در محفظهای که از $$\large N$$ سطح با دماهای مختلف تشکیل شده، به صورت زیر تعریف میشود.
$$\large T_ {\text {surr}} \:\cong\: F_ {\text {person-1}} \times T_1 \:+\: F_ {\text {person-2}} \times T_2 \:+\: ... \:+\: F_ {\text {person-N}} \times T_N$$
در رابطه بالا، دمای سطح $$\large i$$ با $$\large T_i$$ نشان داده شده و ضریب دید بین انسان و سطح $$\large i$$ برابر $$\large F_ {\text {person-i}}$$ است.
افت حرارت محسوس خالص را میتوانیم به صورت مجموع دو افت حرارتی جابجایی و تشعشعی بیان کنیم.
$$\large \dot{Q} _{\text {conv+rad}} \:=\: h_ {\text{combined}} A_ {\text {clothing}} (T_ {\text {clothing}} \:-\: T_ {\text {operative}}) \\~\\
\large =\: (h_ {\text {conv}} \:+\: h_ {\text {rad}}) A_{\text {clothing}} \:(T_ {\text {clothing}} \:-\: T_ {\text {operative}})$$
پارامتر $$\large T_ {\text {operative}}$$ را دمای عملکرد (Operative Temperature) مینامیم و آن را به عنوان میانگین وزنی دماهای تشعشع و محیط تعریف میکنیم. ضرایب به کار رفته در این میانگین وزنی، همان ضرایب انتقال حرارت جابجایی و تشعشع است. به شکل زیر توجه کنید.
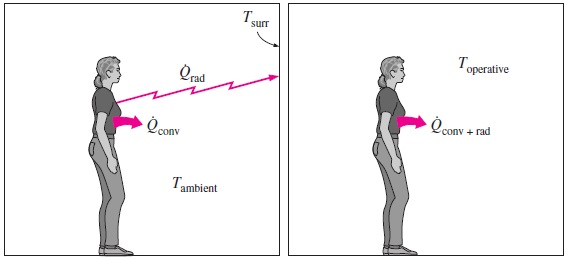
$$\large T_ {\text {operative}} \:=\: \frac {h_ {\text {conv}} T_ {\text {ambient}} \:+\: h_ {\text {rad}} T_ {\text {surr}}} {h_ {\text {conv}} \:+\: h_ {\text {rad}}} \:\cong\: \frac {T_ {\text {ambient}} \:+\: T_ {\text {surr}}} {2}$$
اگر ضرایب انتقال حرارت جابجایی و تشعشعی با هم مساوی باشند، میانگین وزنی بالا به میانگین معمولی تبدیل میشود. شاخص دیگری که در آنالیز انتقال حرارت بدن انسان اهمیت زیادی دارد، دمای مؤثر (Effective Temperature) است. دمای مؤثر، اثرات دما و رطوبت را تجمیع میکند. دو محیط مختلف با دمای مؤثر یکسان، تأثیرات مشابهی در انتقال حرارت بدن انسان دارد. حتی اگر هم دما و هم رطوبت با هم تفاوت داشته باشند.
رابطه انتقال حرارت از طریق لباس به شکل زیر است.
$$\large \dot{Q}_ {\text {conv+rad}} \:=\: \frac {A_ {\text {clothing}} (T_ {\text {skin}} \:-\: T_ {\text {clothing}}) } {R_ {\text {clothing}}}$$
واحد اندازهگیری $$\large R_ {\text {clothing}}$$، برابر با $$\large m^2.\: ^\circ C/W$$ است و شامل مجموع اثرات هدایت، جابجایی و تشعشع بین پوست و سطح بیرونی لباس میشود. مقاومت گرمایی لباس معمولاً برحسب واحدی به نام $$\large clo$$ بیان میشود که تعریف آن، به صورت زیر است.
$$\large 1\:clo \:=\: 0.155\: m^2. \:^\circ C/W \:=\: 0.880\: ft^2. \: ^\circ F. \:h/ Btu$$
به این ترتیب، به جای اینکه افت حرارتی محسوس خالص را برحسب دمای لباس تعریف کنیم، میتوانیم آن را به شکل زیر و به عنوان تابعی از دمای پوست بنویسیم.
$$\large \dot{Q} _{\text {conv+ rad}} \:=\: \frac {A_{ \text {clothing}} (T_{\text {skin}} \:-\: T_{\text {operative}})} {R_ {\text {clothing}} \:+\: \frac {1} {h_ {\text {combined}}}}$$
در وضعیتی که به عنوان آسایش حرارتی (Thermal Comfort) تعریف میشود، دمای متوسط پوست بدن در حدود $$\large 33^ \circ C$$ (معادل $$\large 91.5^ \circ F$$) بوده و بازه تغییرات مجاز آن نیز برابر $$\large \pm1.5^ \circ C$$ (معادل $$\large \pm2.5^ \circ F$$) است. افت حرارت نهان از طریق پوست، با اختلاف بین فشار بخار آب در پوست و هوای محیط و همچنین درجه رطوبت پوست متناسب است. افت حرارت نهان، ناشی از مجموع اثرات تبخیر عرق و تراوش آب از طریق پوست است.
$$\large \dot{Q} _{\text {latent}} \:=\: \dot{m} _{\text {vapor}} h_{fg}$$
در رابطه بالا، $$\large \dot{m} _{\text {vapor}}$$ نرخ تبخیر آب از بدن است و با واحد $$\large kg/s$$ سنجیده میشود. $$\large h_{fg} $$ نیز آنتالپی تبخیر آب بوده و مقدار آن در دمای $$\large 30\: ^\circ C$$ برابر با $$\large 2430\: kJ/kg$$ است.
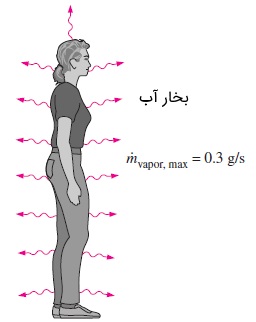
هنگامی که بدن کاملاً خیس باشد، افت حرارت از طریق تبخیر به ماکزیمم مقدار خود میرسد. در سوی مقابل، لباس به عنوان عایقی در برابر تبخیر عمل میکند و نرخ تبخیر در فردی که لباس به تن دارد، به تراوایی رطوبت در لباس بستگی دارد. نرخ تبخیر ماکزیمم در یک فرد متوسط، در حدود $$\large 1\: L/h$$ (معادل $$\large 0.3\: g/s$$) است. بدن انسان میتواند در خلال انجام حرکات ورزشی در یک روز گرم، تا $$\large 2\: kg$$ آب را در هر ساعت از دست بدهد. ولی پس از این مقدار، عرق به صورت مایع روی پوست مانده و تبخیر نخواهد شد.
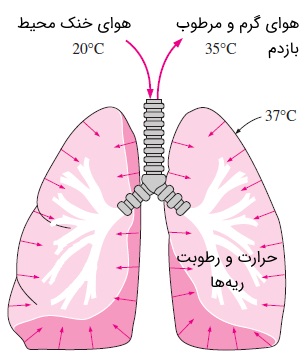
هنگام دم و بازدم، هوایی که وارد ریهها میشود، تقریباً در شرایط محیط است و هوایی که از ریهها خارج میشود، در دمایی نزدیک به دمای داخل بدن، در حالتی نزدیک به اشباع قرار دارد. بنابراین، بدن به صورت همزمان، از طریق جابجایی، گرمای محسوس را از دست میدهد و همچنین از طریق تبخیر، گرمای نهان را دفع میکند. این بخش از اتقال حرارت بدن انسان را میتوان با روابط زیر نشان داد.
$$\large \dot{Q} _{\text {conv, lungs}} \:=\: \dot{m} _{\text {air, lungs}} \times \:C_{p, \text {air}} (T_ {\text {exhale}} \:-\: T_ {\text {ambient}}) \\~\\
\large \dot{Q} _{\text {latent, lungs}} \:=\: \dot{m} _{\text {vapor, lungs}} \times \:h_{fg} \:=\: \dot{m} _{\text {air, lungs}} \times \:(w_ {\text {exhale}} \:-\: w_ {\text {ambient}}) h_{fg}$$
در دو رابطه بالا، نرخ ورود هوا به ریهها با $$\large \dot{m} _{\text {air, lungs}}$$ نشان داده شده و واحد سنجش آن نیز $$\large kg/s$$ است. $$\large C_{p, \text {air}}$$، ظرفیت گرمایی ویژه هوا را نشان داده و مقدار آن $$\large 1.0\: kJ/kg.\: ^\circ C$$ است. همچنین $$\large w$$ نیز به نسبت رطوبت اشاره دارد و به صورت جرم رطوبت در واحد جرم هوای خشک اندازهگیری میشود.
نرخ ورود هوا به ریهها مستقیماً با نرخ متابولیک $$\large \dot{Q} _{\text {met}}$$ متناسب است. نرخ افت حرارت خالص از ریهها در حین تنفس به صورت زیر تعریف میشود.
$$\large \dot{Q} _{\text {conv + latent, lungs}} \:=\: 0.0014\: \dot{Q}_ {\text {met}}\: (34\:-\: T_ {\text {ambient}}) \\~\\
\large +\: 0.0173\: \dot{Q}_ {\text {met}}\: (5.87 \:-\: P_ {v, \text {ambient}})$$
در رابطه بالا، فشار بخار هوای محیط، با نماد $$\large P_ {v, \text {ambient}}$$ و واحد اندازهگیری $$\large kPa$$ وارد میشود. درصدی که گرمای محسوس به خود اختصاص میدهد، از حدود $$\large 40$$ درصد در کار سنگین تا $$\large 70$$ درصد در کار سبک متغیر است. بقیه انرژی به شکل گرمای نهان و از طریق تعریق بدن خارج میشود.
مثال: تأثیر لباس روی انتقال حرارت بدن انسان
سؤال: میدانیم انسان در حالتی که دمای پوستش در حدود $$\large 33\: ^\circ C$$ باشد، احساس آسایش میکند. فرد متوسطی با مساحت $$\large 1.8\: m^2$$ را در نظر بگیرید که لباس تابستانی با مقاومت گرمایی $$\large 0.6\: clo$$ به تن کرده باشد.
ایستادن در اتاقی با دمای $$\large 22\: ^\circ C$$ برای این فرد، احساس آسایش به همراه دارد. از جریان هوا در اتاق صرف نظر کرده و دمای سطوح نزدیک به فرد را برابر با دمای اتاق فرض کنید. به منظور فراهم بودن آسایش حرارتی برای این فرد در حالت بدون لباس، دمای اتاق باید روی چه عددی تنظیم شود؟ (هنگامی که سرعت هوا پایین باشد، ضریب انتقال حرارت جابجایی را برای فردی که ایستاده، برابر با $$\large 4.0\: W/m^2. \:^\circ C$$ و ضریب انتقال حرارت تشعشعی را $$\large 4.7\: W/m^2. \:^\circ C$$ فرض کنید.)
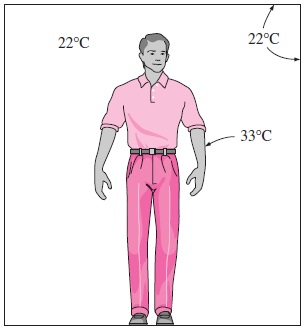
پاسخ: شرایط مسأله را پایدار و ضرایب انتقال حرارت را ثابت فرض میکنیم. انتقال حرارت بدن فرد به دو شکل محسوس و نهان اتفاق میافتد. گرمای محسوس شامل انتقال حرارت بدن از طریق جابجایی و تشعشع است. ضریب انتقال حرارت سطحی را میتوان به صورت زیر و برابر با مجموع ضرایب انتقال حرارت جابجایی و تشعشعی تعریف کرد.
$$\large h_{\text {combined}} \:=\: h_{\text {conv}} \:+\: h_{\text {rad}} \:=\: 4.0 \:+\: 4.7 \\~\\
\large \Rightarrow ~~~ h_{\text {combined}} \:=\:8.7\: W/m^2.\: ^\circ C$$
برای تبدیل واحد مقاومت گرمایی لباس به شیوه زیر عمل میکنیم.
$$\large R_{\text {clothing}} \:=\: 0.6\: clo \:=\: 0.6 \times 0.155\: m^2.\: ^\circ C/W \\~\\
\large R_{\text {clothing}} \:=\: 0.093\: m^2.\: ^\circ C/W$$
افت حرارت محسوس از بدن این فرد در حالت پوشیده به صورت زیر است.
$$\large \dot{Q}_ {\text {sensible, clothed}} \:=\: \frac {A_s (T_ {\text {skin}} \:-\: T_ {\text {ambient}})} {R_ {\text {clothing}} \:+\: \frac {1} {h_ {\text {combined}}}} \\~\\
\large =\: \frac {(1.8\: m^2) (33\:-\:22) ^\circ C} {0.093\: m^2. ^\circ C/W \:+\: \frac {1} {8.7 \: W/m^2.\: ^\circ C}} \\~\\
\large \Rightarrow ~~~ \dot{Q}_ {\text {sensible, clothed}} \:=\: 95.2\:W$$
از نظر انتقال حرارت، نپوشیدن لباس، با برداشتن عایق یا صفر شدن مقاومت $$\large R_ {\text {clothing}}$$ معادل است. اکنون میتوانیم معادله انتقال حرارت بدن را در حالت بدون عایق بنویسیم.
$$\large \dot{Q}_ {\text {sensible, unclothed}} \:=\: \frac {A_s (T_ {\text {skin}} \:-\: T_ {\text {ambient}})} {\frac {1} {h_ {\text {combined}}}} \:=\: \frac {(1.8\: m^2) (33 \:-\: T_ {\text {ambient}}) ^\circ C} {\frac {1} {8.7\: W/m^2. \:^\circ C}}$$
برای اینکه در حالت بدون لباس هم آسایش حرارتی حفظ شود، دمای پوست و فرد و نرخ انتقال حرارت از او باید ثابت باقی بماند. از این رو، معادله بالا را برابر با $$\large 95.2\: W$$ قرار میدهیم. در نتیجه، دمای محیط، مساوی با $$\large T_{ \text {ambient}} \:=\: 26.9\: ^\circ C$$ به دست میآید. توجه کنید که در این سؤال برای محاسبه انتقال حرارت بدن انسان، از اثر پوشیدن یا نپوشیدن لباس روی حرارت نهان، چشمپوشی شده و برای سادگی حل مسأله، مساحت فرد را در هر دو حالت یکی فرض کردیم.
در صورت علاقهمندی به مباحث مرتبط در زمینه مهندسی مکانیک، آموزشهای زیر نیز پیشنهاد میشوند:









