اثر کامپتون — به زبان ساده
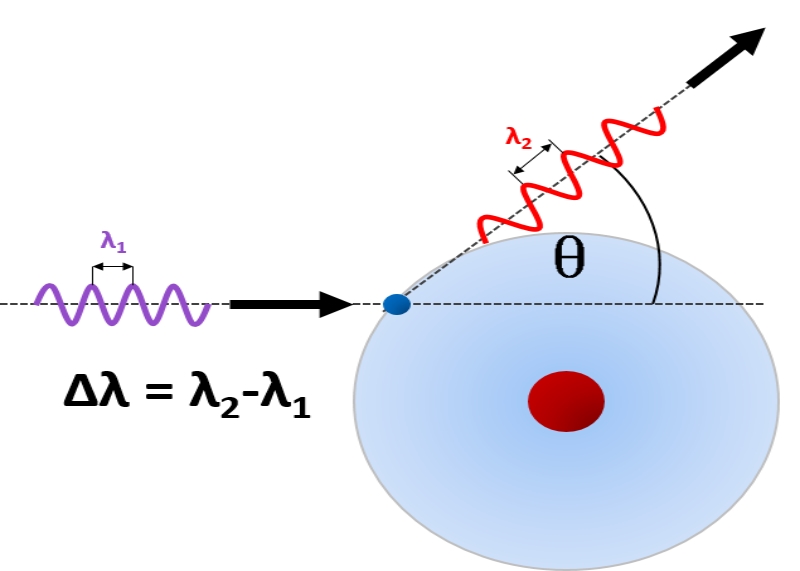
اگر مطلب کوانتوم -- به زبان ساده را مطالعه کرده باشید، احتمالا متوجه شدهاید که یکی از فرضیات اساسی فیزیک کوانتوم این است که الکترون، نور یا حتی یک جسم میتواند از زاویههای متفاوتی بهصورت موج یا ذره دیده شود. برای مدتهای بسیاری این تصور وجود داشت که نور ماهیتی موجی دارد؛ اما آلبرت انیشتین برای اولین بار فرض ذرهای بودن نور را مطرح کرد. اثر کامپتون یکی از اثباتهای انجام شده در فیزیک است که با استفاده از آن میتوان رفتار دوگانه نور را توجیه کرد. از این رو در این مطلب قصد داریم تا این اثر را توضیح داده و مثالی نیز از آن ارائه کنیم.
موجی-ذرهای بودن نور
دو نظریه بنیادی انیشتین که در سال 1905 مطرح شدند، نظریه نسبیت خاص و مفهوم کوانتومی نور بود که امروزه به آن فوتون گفته میشود. در سالهای بعد نیز انیشتین بر این موضوع تاکید داشت که امواج الکترومغناطیسی از فوتونها تشکیل شدهاند؛
همانگونه که مواد از ذراتی همچون الکترون ساخته شدهاند. پرتویی از نور با طول موج $$ \lambda $$ را میتوان همچون یک موج کلاسیک یا مجموعهای از ذرات فوتون در نظر گرفت که با سرعت نور در حال حرکت هستند. هریک از این ذرات حامل انرژی به اندازه $$ E _ f = h f $$ است. در حقیقت انرژی تمامی این ذرات برابر با این مقدار است. این توصیف بهخوبی میتوانست تعامل نور با ماده را توجیه کند.

تکانه فوتون
بر خلاف ذرات ماده که جرم آنها برابر با مقدار مشخص $$ m _ 0 $$ است، یک فوتون بدون جرم محسوب میشود. همچنین علیرغم ذرههای ماده که با سرعت مشخصی در خلاء حرکت میکنند، یک فوتون دقیقا با سرعت نور در خلاء حرکت میکند.
از نظر مکانیک کلاسیک نیوتونی، این دو ویژگی به این معنی است که مفهومی همچون فوتون نباید وجود داشته باشد. برای مثال، چطور میتوان انرژی حرکتی یا انرژی جنبشی جسمی بدون جرم را پیدا کرد؟ این پارادوکس ظاهری زمانی قابل حل شدن است که یک فوتون را به عنوان یک ذره نسبیتی در نظر بگیریم. با توجه به نظریه نسبیت خاص، هر ذره در طبیعت از معادله انرژی نسبیتی پیروی میکند. این معادله به صورت زیر بیان میشود.
$$ E ^ 2 = p ^ 2 c ^ 2 + m _ 0 ^ 2 c ^ 4 $$
رابطه فوق را میتوان برای یک فوتون نیز بیان کرد. در این معادله $$ E $$ نشاندهنده کل انرژی ذره، $$ p $$ نشاندهنده تکانه و $$ m _ 0 $$ جرم سکون را نشان میدهد. برای یک فوتون، به شکلی ساده میتوان از $$ m _ 0 = 0 $$ استفاده کرد. با انجام این کار تکانه فوتون برابر با مقدار زیر بدست میآید.
$$ p _ f = \dfrac { E _ f } { c } $$
مقدار انرژی را نیز برابر با $$ h f $$ در نظر بگیرید. در این صورت انرژی بر حسب فرکانسِ $$ f $$ یا طول موجِ $$ \lambda $$ برابر میشود با:
$$ E _ f = h f = \dfrac { h c } { \lambda } $$
رابطه بین $$ f $$ و $$ \lambda $$ را نیز میتوان با استفاده از سرعت نور ($$ c $$) بهشکل زیر بیان کرد:
$$ E _ f = h f = \dfrac { h c } { \lambda } $$
در نتیجه مقدار تکانه برابر میشود با:
$$\color {white} {p _ f = \dfrac { h } { \lambda }} p _ f = \dfrac { h } { \lambda } \color {white} {p _ f = \dfrac { h } { \lambda }} $$
همانطور که احتمالا میدانید مشخصه تکانه، کمیتی برداری است. در حقیقت تکانه هم دارای اندازه و هم دارای جهت است. مقدار بیان شده در بالا تنها اندازه تکانه را نشان میدهد. شکل برداری رابطه فوق بهصورت زیر است.
$$ \color {white} {p _ f = \dfrac { h } { \lambda }} \overrightarrow { p } _ f = \hbar \overrightarrow { l } \color {white} { p _ f = \dfrac { h } { \lambda } } $$
در رابطه فوق $$ \hbar = h/2\pi $$ ثابت کاهیده پلانک بوده که معادل با تقسیم ثابت پلانک به مقدار $$ 2 \pi $$ است. $$ \overrightarrow { l } $$ برابر با بردار موج یا بردار انتشار است. این بردار نشاندهنده جهت تکانه فوتون است. اندازه بردار موج برابر با $$ k = |\overrightarrow{k}| = 2 \pi / \lambda $$ بوده که به آن عدد موج گفته میشود.
اثر کامپتون
اثر کامپتون عنوانی است که به از دست رفتن انرژی پرتوهای ایکس در نتیجه برخورد به یک ماده گفته میشود. طبق فیزیک کلاسیک هنگامی که یک موج الکترومغناطیسی به اتمهای ماده برخورد کند طول موج پرتو نوری پخش شده باید برابر با طول موجِ فرودی باشد. بر خلاف این پیشبینی صورت گرفته توسط فیزیک کلاسیک، مشاهدات نشان میدهند که در هنگام برخورد موجی با طول موج مشخص به مادهای همچون گرافیت، پرتوهای منحرف شده طول موجی متفاوت نسبت به طول موج ورودی دارند.
این پدیده توجیه نشده توسط فیزیک کلاسیک، در سال ۱۹۲۳ توسط آرتور کامپتون و همکارانش مورد مطالعه قرار گرفت. بهمنظور توضیح این پدیده، کامپتون از نظریه ذرهای بودن نور که توسط انیشتین ارائه شده بود استفاده کرد. اثر کامپتون تاثیری شگرف در فیزیک داشت چرا که برای اولین بار مشخص شد که نمیتوان تابش الکترومغناطیسی را بهصورت کاملا موجی در نظر گرفت. توضیح کامپتون برای اولین بار نشان داد که میتوان امواج الکترومغناطیسی را به عنوان ذرات فوتون در نظر گرفت.
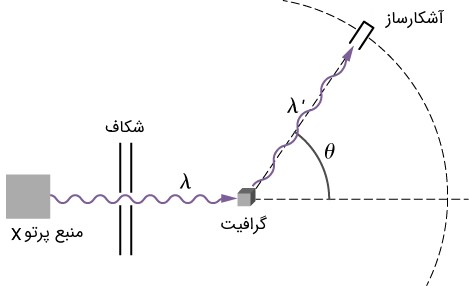
در شکل فوق شماتیک آزمایش انجام شده توسط کامپتون ترسیم شده است. همانطور که در این شکل نیز نشان داده شده، نحوه انجام آزمایش بسیار ساده است. در حقیقت در ابتدا امواج $$ X $$ با طول موج $$ \lambda $$ به نمونهای گرافیتی برخورد داده میشوند. در نتیجه این امواج با اتمهای گرافیت برهمکنش نشان میدهد. امواج با طول موج جدید $$ \lambda ^ { \prime } $$ منحرف شده و اندازه طول موج توسط یک آشکارساز معلوم میشود. این آشکارساز در زاویهای مشخص نسبت به پرتو ورودی قرار داده شده و شدت پرتو بازتابیده را اندازهگیری میکند. نتایج اولیه آزمایش در شکل زیر نشان داده شده است. در نتایج نشان داده شده محور $$ x $$ نشاندهنده طول موج پرتو منحرف شده و محور عمودی نشاندهنده شدت این پرتوها است.

طبق نمودارهای فوق، به ازای تمامی زوایای اندازهگیری شده (به جز $$ \theta = 0 $$)، دو قله برای شدت پرتو بدست آمده است. یکی از قلهها در طول موج $$ \lambda $$ رخ داده و دیگری در طول موجی به فاصله $$ \delta \lambda $$ به فاصله طول موج اول اتفاق میافتد. همانطور که مشاهده میکنید اندازه این اختلاف با افزایش زاویه از صفر درجه، افزایش مییابد. به فاصله $$ \delta \lambda $$ «جابجایی کامپتون» (Compton Shift) گفته میشود.
جابجایی کامپتون
همانطور که توسط کامپتون نیز توضیح داده شد، الکترونهای موجود در اتم گرافیت تقریبا بهصورتی آزادانه حرکت میکنند. کامپتون اشعه $$ X $$ وارد شده به اتمهای گرافیت را بهصورت مجموعهای از فوتونها در نظر گرفت. فوتونهای ورودی، به الکترونهای لایه والانس اتمهای گرافیت برخورد میکنند. در نتیجه برخورد فوتونها با الکترونها، بخشی از انرژی و تکانه آنها از دست رفته، در نتیجه فوتونها نسبت به مسیر اولیهشان منحرف میشوند. این مدل بهشکل کیفی علت طول موجهای بزرگتر فوتونهای منحرف شده را توضیح میدهد. در حقیقت فوتونی که انرژیش را از دست داده دارای فرکانس کمتری یا بیانی معادل دارای طول موجی بزرگتر است. کامپتون به منظور اثبات درستی تفسیرش از نتایج آزمایش انجام داده شده، تلاش کرد تا مدلی تحلیلی از نحوه برخورد فوتونها به الکترونها ارائه دهد.
در بدست آوردن روابط تحلیلی، او دو فرض اصلی را در نظر گرفت:
- قانون پایستگی تکانه خطی
- قانون پایستگی مجموع انرژی ذرات
بهمنظور به دست آوردن جابجایی کامپتون او از نمادهای $$ E _ f $$ و $$ \overrightarrow { p } _ f $$ بهمنظور نشان دادن انرژی و تکانه فوتونِ برخوردی استفاده کرد. توجه داشته باشید که فرکانس فوتون نیز برابر با $$ f $$ نشان داده شده است. الکترون بهصورت نسبی، ساکن در نظر گرفته شده است. این جمله به معنای آن است که درست قبل از برخورد فوتون، کل انرژی الکترون برابر است با:
$$ m _ 0 c ^ 2 $$
درست پس از برخورد انرژی و تکانه الکترون بهترتیب برابر با $$ E $$ و $$ \overrightarrow { p } $$ میشود. به همین ترتیب انرژی و تکانه فوتون نیز پس از برخورد را برابر با $$ \overrightarrow { \tilde { E } } _ f $$ و $$ \overrightarrow { \tilde { p } } _ f $$ در نظر بگیرید. البته همانطور که گفته شد فرکانس فوتون نیز پس از برخورد به $$ f ^ { \prime } $$ تغییر میکند. مسیر ورود فوتون نیز به صورت افقی بوده که با زاویه $$ \theta $$ منحرف میشود. زاویه $$ \theta $$ برابر با زاویه بین دو بردار $$ \overrightarrow { p } _ f $$ و $$ \overrightarrow { \tilde { p } } _ f $$ است. در حقیقت با استفاده از رابطه زیر میتوان اندازه این زاویه را بدست آورد.
$$ \overrightarrow { p } \cdot \overrightarrow { \tilde { p } } _ f = p _ f \tilde { p } _ f \cos \, \theta $$
با توجه به فرض کامپتون میتوان گفت که برخورد الکترون و فوتون در فضایی ایزوله صورت میگیرد. برای این سیستم قانون پایستگی انرژی، قبل و پس از برخورد را میتوان به شکل زیر نوشت.
$$ \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E} E _ f + m _ 0 c ^ 2 = \tilde { E } _ f + E \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E} $$
سمت چپ معادله فوق نشاندهنده انرژی کل سیستم قبل از برخورد است. بدیهی است که سمت راست نیز نشاندهنده کل انرژی سیستم درست پس از برخورد است. به همین صورت پایستگی تکانه را نیز میتوان برای قبل و پس از برخورد بهشکل زیر نوشت:
$$ \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } \overrightarrow { p } _ f = \overrightarrow { \tilde { p } } _ f + \overrightarrow { p } \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
سه معادله ارائه شده در بالا کل فیزیک برخورد را در خود دارد و مابقی تنها عملیاتهایی جبری محسوب میشوند. بهمنظور دستیابی به جابجایی کامپتون در اولین گام معادله انرژی را بهشکل زیر بازنویسی میکنیم.
$$ \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } [ ( E _ f - \tilde { E } _ f ) + m _ 0 c ^ 2 ] ^ 2 = E ^ 2 \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
در قدم بعدی از رابطه انرژی فوتون ($$ E _ f = h f = \dfrac { h c } { \lambda} $$) استفاده کرده و معادله فوق را بهصورت زیر بازنویسی میکنیم.
$$ \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } (E_f / c - \tilde { E } _ f / c ) ^ 2 + 2 m _ 0 c ( E _ f / c - \tilde { E } _ f / c ) = p ^ 2 \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
حال میتوان از رابطه تکانه ($$ p _ f = \dfrac { h } { \lambda } $$) استفاده کرده و معادله فوق را بر حسب تکانه، بهصورت زیر نوشت.
$$ ( p _ f - \tilde { p } _ f ) ^ 2 + 2 m _ 0 c ( p _ f - \tilde { p } _ f ) = p ^ 2 $$
بهمنظور حذف کردن $$ p ^ 2 $$ میتوان از معادله تعادل تکانه استفاده کرد. با استفاده از تعادل تکانه رابطه فوق بهصورت زیر قابل بازنویسی میشود.
$$ \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } ( \overrightarrow { p } _ f - \overrightarrow { \tilde { p } } _ f )^ 2 = p ^ 2 \, , \, ( \overrightarrow { p } _ f - \tilde { p } _ f ) = p _ f ^ 2 + \tilde { p } _ f ^ 2 - 2 p _ f \tilde { p } _ f \, \cos \, \theta. \color {white} {m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
رابطه ضرب داخلی بردارهای تکانه در بالا ارائه شده است. نهایتا رابطه بین زاویه $$ \theta $$ و دیگر پارامترها بهصورت زیر بدست میآید.
$$ \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } (p_f - \tilde { p } _ f ) ^ 2 + 2 m _ 0 c ( p _ f - \tilde { p } _ f ) = p _ f ^ 2 + \tilde { p }_ f ^ 2 - 2p_f \tilde { p } _ f \, \cos \, \theta. \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
با اندکی عملیاتی ریاضیاتی، رابطه فوق را میتوان بهصورت زیر نیز بیان کرد:
$$ \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } \dfrac{1}{ \tilde { p } _ f } - \dfrac { 1 } { p _ f} = \dfrac { 1 } { m _ 0 c } ( 1 - \cos \, \theta) \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
ازطرفی رابطه بین تکانهها و طول موجها قبل و پس از برخورد نیز بهترتیب برابر با $$ 1 /\tilde { p } _ f = \lambda ^ { \prime } /h $$ هستند. با قرار دادن این دو رابطه در رابطه فوق، اختلاف بین طول موجها، قبل و پس از برخورد برابر میشوند با:
$$ \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } \lambda ^ { \prime } - \lambda = \dfrac { h } { m _ 0 c } ( 1 - \cos \, \theta) \color {white} { m _ 0 c ^ 2 = \tilde { E } _ f + E } $$
به ضریب $$ h / m _ 0 c $$، طول موج کامپتونِ الکترون گفته میشود که اندازه آن نیز برابر است با:
$$ \lambda _ c = \dfrac { h } { m _ 0 c } = 0.00243 \, n m = 2 . 4 3 \, pm $$
با نشان دادن اختلاف طول موج با $$ \Delta \lambda = \lambda ^ { \prime } - \lambda $$، نهایتا این مقدار برابر با رابطه زیر بدست میآید.
$$ \Delta \lambda = \lambda _ c ( 1 - \cos \, \theta ) $$
رابطه فوق بهخوبی نمودارهای بدست آمده در شکل ۲ را توجیه میکند. آزمایشهای انجام شده با مولیبدن، گرافیت، کلسیت و بسیاری دیگر از مواد، درستی رابطه فوق را تایید میکند.
مثال ۱
پرتوی $$ X $$ با طول موج 71 پیکومتر به هدفی کانی شکل برخورد داده میشود. طول موج پرتو بازتابیده شده در زاویه ۳۰ درجه را بیابید. همچنین بیشترین میزان تغییر طول موج در این آزمایش چقدر است؟
به منظور یافتن طول موج بازتابیده شده در اولین گام باید اندازه جابجایی کامپتون را بیابیم. مقدار جابجایی به ازای زاویه ۳۰ درجه برابر است با:
$$ \color {white}{\Delta \lambda = \lambda _ c ( 1 - cos \,} \Delta \lambda = \lambda _ c ( 1 - cos \, 30 ° ) = 0.134 \lambda_c = ( 0.134 ) ( 2.43 ) \, pm = 0.32 \nonumber \color {white}{\Delta \lambda = \lambda _ c ( 1 - cos \,} $$
بنابراین طول موج بازتابیده شده نیز برابر میشود با:
$$ \color {white}{\Delta \lambda = \lambda _ c ( 1 - cos \,} \lambda ^ { \prime } = \lambda + \Delta \lambda = ( 71 + 0.325 ) \, p m = 71.325 p m. \nonumber \color {white} { \Delta \lambda = \lambda _ c ( 1 - cos \, } $$
همچنین بیشترین میزان تغییر طول موج در زاویه ۱۸۰ رخ میدهد. اندازه این تغییر نیز برابر با مقدار زیر بدست میآید.
$$ \color {white}{\Delta \lambda = \lambda _ c ( 1 - cos \,} (\Delta \lambda ) _ { max } = \lambda _ c ( 1 − cos \, 180°) = 2 ( 2.43 \, pm) = 4.86 \, pm \nonumber \color {white} { \Delta \lambda = \lambda _ c ( 1 - cos \, } $$
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی و فیزیک، آموزشهای زیر نیز به شما پیشنهاد میشوند:
^^











در معادله حاصلضرب نقطه ای تکانه فوتون و تکانه الکترون
سمت راست تکانه فوتون نباید علامت بردار داشته باشه. باید علامت تیلد داشته باشه
با سلام،
فرمول موردنظر بررسی و اصلاح شد،
با تشکر از همراهی شما با مجله فرادرس
داداش اگه ی کلیپ هم براش میساختین که عالی تر میشد
چون که کلیپای واقعا جذابی درست میکنین
ببخشید در انرژی نسبیتی یک جسم بنظرم E^2 باشد نه اندیس چون عدد 2 در اندیس ، معادله رو اشتباه کرده
باتشکر
با سلام و تشکر از توجه شما؛ اندیس انرژی اصلاح شد.
ممنونم از شما بزرگوار
اها پس منظور شما اینه که فقط تکانه سمت راست معادله برداری هست؟؟
بله. در حقیقت پایستگی انرژی، یک معادله اسکالر و پایستگی تکانه، یک معادله برداری را نتیجه میدهند. با برابر قرار دادن این دو معادله، اختلاف طول موج ورودی و طول موج بازتاب شده بدست میآید.
درسته اخه cos که در سمت چپ معادله بدلیل برداری بودن تکانه بوجود میاد رو چطور حذف کردید؟؟
دوست عزیز ترم کسینوس در معادله حذف نشده است. کافی است دو عبارت $$ (\overrightarrow { p } _ f – \overrightarrow { \tilde { p } } _ f )^ 2 = p ^ 2 $$ و $$ ( p _ f – \tilde { p } _ f ) ^ 2 + 2 m _ 0 c ( p _ f – \tilde { p } _ f ) = p ^ 2 $$ را با هم برابر قرار دهید.
ببخشید منظورم اینه که چهارمین رابطه از پایین رو با چع عملیات ریاضی بدست اوردید؟؟
با باز کردن عبارتهای سمت چپ خواهید دید که مقادیر توان دوم p و $$\tilde { p }$$ از سمت چپ و راست معادله حذف خواهند شد. در مرحله بعد با تقسیم کردن طرفین رابطه به $$ p \tilde { p }$$، معادله زیر بدست میآید.
$$\dfrac{1}{ \tilde { p } _ f } – \dfrac { 1 } { p _ f} = \dfrac { 1 } { m _ 0 c } ( 1 – \cos \, \theta) $$
سلام اگه میشه یکم کاملتر توضیح بدید که چطور فرمول نهایی رو استخراج کردید
با تشکر
با سلام و تشکر از بازخورد ارائه شده.
به منظور دستیابی به رابطه نهایی، مقدار h/m0c (رابطه یکی مانده به آخر) با طول موج اشعه ورودی جایگزین شده است. خودِ رابطه ماقبل آخر نیز با نوشتن پایستگی خطی تکانه سیستم (فوتون+الکترون) و همچنین نوشتن پایستگی انرژی سیستم، قبل و پس از برخورد بدست میآید.