نرخ تغییرات در ریاضی – به زبان ساده
در این قسمت قصد داریم تا در مورد یکی از مهمترین کاربردهای مشتق صحبت کنیم. در حقیقت این کاربرد در محاسبه نرخ تغییرات یک کمیت است. کمیت متغیر میتواند نیرو، جرم سوخت در معادله موشک یا هر پارامتر دیگری باشد. به منظور درک بهتر پیشنهاد میشود مطالب مفاهیم تابع و ماکزیمم و مینیمم تابع را مطالعه فرمایید.


نرخ تغییرات
همانطور که پیشتر نیز بیان شد، نشان دهنده نرخ تغییرات تابع است. بنابراین اگر این تابع نشان دهنده مقدار حجم آب در یک مخزن باشد، مشتق زمانی آن میتواند به ما دبی آب وارد شده به مخزن را نشان دهند. یا ممکن است این تابع نشان دهنده ارتفاع یک فضاپیما باشد، بنابراین مشتق آن به ما سرعت عمودی این فضاپیما را نشان میدهد.
این مطلب چیزی نیست جز مثالهایی از محاسبه نرخ تغییرات. از این رو در ادامه مثالهایی ارائه شده که در آنها نحوه بدست آوردن نرخ تغییرات تابع توضیح داده شده است.
مثال ۱
تابع زیر در چه نقاطی تغییر نمیکند؟
در اولین گام باید مشتق تابع فوق را محاسبه کنیم.
تغییر نکردن تابع به معنای یافتن نقطهای است که در آن نرخ تغییرات برابر با صفر باشد. در نتیجه با صفر قرار دادن مشتق تابع داریم:
در مطلب حل معادلات مثلثاتی، نحوه حل این گونه از معادلات را توضیح دادیم. بنابراین پاسخ معادله فوق برابر است با:
$$\large \begin{alignat}{4} 2 x = & 0.3047 + 2 \pi n & & \hspace {0.5in} \, \, \, \,{\mbox{OR}}\hspace{0.5in} \, \, \, \, & 2 x = & 2.8369 + 2 \pi n & & \hspace {0.25in} n = 0, \pm 1, \pm 2, \ldots \\ x = & 0.1524 + \pi n & & \hspace {0.5in} \, \, \, \, {\mbox{OR} } \hspace {0.5in} \, \, \, & x = & 1.4185 + \pi n & & \hspace{0.25in}n = 0, \pm 1, \pm 2, \ldots \end{alignat} $$
مثال ۲
تابع زیر در کدام نواحی، نزولی و در کجاها صعودی است.
همانطور که در مثال اول نیز بیان شد، در ابتدا باید از تابع فوق مشتق گرفته شود.
در گام بعد باید محلی را بیابیم که در آن تابع تغییراتی ندارد. شکل عبارت فوق نشان میدهد که یکی از پاسخها برابر با است. نهایتا سه پاسخِ معادله فوق برابرند با:
بنابراین مشتقِ تابع در سه نقطه تغییراتی ندارد. با تعیین علامت عبارتِ مشتق به صورت زیر، محلهای صعودی و نزولیِ تابع اصلی بدست خواهند آمد.
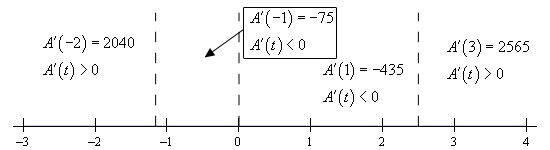
بنابراین نواحی افزایشی و کاهشی به صورت زیر بدست میآیند.
مثال ۳
دو خودرو که در فاصله مایل از یکدیگر قرار گرفتهاند ناگهان شروع به حرکت میکنند. خودروی در سمت غرب خودروی قرار گرفته و با سرعت مایل بر ساعت به سمت آن حرکت میکند. این در حالی است که به طور همزمان خودروی با سرعت مایل بر ساعت به سمت جنوب در حال حرکت است. پس از گذشت ساعت، فاصله بین دو خودرو با چه سرعتی تغییر میکند؟
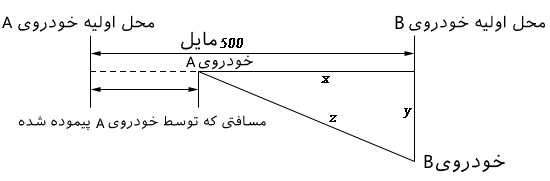
همانطور که در شکل فوق نیز نشان داده شده، نشان دهنده فاصله عمودی دو خودرو و نشان دهنده فاصله افقی آنها است. از طرفی فاصله کلی آنها با نشان داده شده. پس از گذشت مدت زمان ساعت، فاصله افقی و عمودی دو خودرو برابر است با:
از طرفی با استفاده از قانون فیثاغورس، فاصله پس از ساعت برابر خواهد بود با:
حال باید مشتق تابع را نسبت به دو متغیر و بیابیم. بدین منظور از مفهوم مشتق ضمنی به صورت زیر استفاده میکنیم.
توجه داشته باشید که در رابطه فوق دو ترمِ و به معنای سرعتهای افقی و عمودی دو خودرو هستند. بنابراین و را در رابطه فوق جایگذاری میکنیم.
بنابراین دو خودرو با سرعت مایل بر ساعت به سمت هم نزدیک میشود.
در صورت علاقهمندی به مباحث مرتبط در زمینه ریاضی، آموزشهای زیر نیز به شما پیشنهاد میشوند:
- مجموعه آموزشهای دروس ریاضیات
- مجموعه آموزشهای ریاضیات و فیزیک پایه
- انتگرال دوگانه در فیزیک — به زبان ساده
- مشتق — به زبان ساده
- انتگرال - به زبان ساده
^^












