مدار متوالی یا مدار سری چیست؟ — به زبان ساده با شکل و مثال

در این مطلب در مورد مدار متوالی صحبت کرده و پارامترهای متفاوت مانند مقاومت، ولتاژ، جریان و خازن را در یک مدار متوالی مورد بررسی و محاسبه قرار می‌دهیم.

مدار متوالی یا مدار سری

یک مدار متوالی یا سری به شکلی است که اجزای آن پشت سر یکدیگر قرار گرفته و به پایانه مثبت و منفی باطری متصل هستند. در ابتدای این نوشتار سه اصلی را که باید در مورد مدارهای متوالی یا سری بیاموزید را شرح خواهیم داد:

• جریان: مقدار جریان از طریق هر جز یا مولفه در مدار متوالی یا سری یکسان است.
• مقاومت: مقاومت کل یک مدار متوالی یا سری برابر با مجموع هر یک از مقاومت‌ها است.
• ولتاژ: ولتاژ منبع تغذیه در مدار متوالی یا سری برابر با جمع افت ولتاژ هر یک از مولفه‌های مدار است.

در ادامه چند نمونه از مدارهای متوالی یا سری ساده را بررسی می‌کنیم و سه اصل بیان شده در بالا را در مورد آن‌ها بررسی می‌کنیم. با یک مدار سری که شامل سه مقاومت و یک باتری است شروع خواهیم کرد که تصویر آن در زیر آمده است:

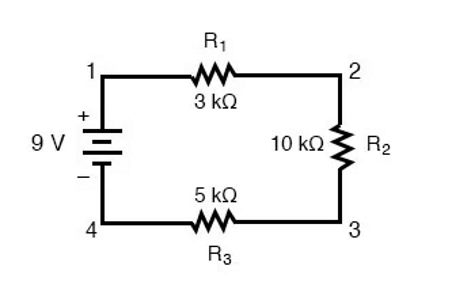
اولین اصل برای تفسیر و توضیح مدار متوالی یا سری به این صورت است که مقدار جریان در یک مدار سری در همه اجزای مدار یکسان است.

دلیل این موضوع آن است که در یک مدار متوالی یا سری فقط یک مسیر برای حرکت جریان وجود دارد و از آنجا که بار الکتریکی در رساناها از طریق چیزی شبیه یک لوله جریان دارد، سرعت جریان در هر نقطه از مدار و در هر زمان خاص باید برابر باشد.

استفاده از قانون اهم در مدار متوالی یا سری

تصویر (1) را در نظر بگیرید، از نحوه قرار گرفتن باتری 9 ولتی می‌توان تشخیص داد که جریان در این مدار در جهت عقربه‌های ساعت از نقطه 1 به 2 تا 3 به 4 و مجدداً تا نقطه 1 شارش خواهد داشت. با این حال در این تصویر یک منبع ولتاژ و سه مقاومت داریم، سوال این است که چگونه از قانون اهم در اینجا استفاده می‌کنیم؟

نکته مهم قانون اهم این است که تمام اجزای یک مدار (ولتاژ، جریان، مقاومت و توان) باید از طریق دو نقطه در مدار با یکدیگر ارتباط داشته باشند. این موضوع را می‌توانیم در نمونه مداری با یک مقاومت در زیر مشاهده کنیم.

استفاده از قانون اهم در یک مدار متوالی ساده و تک مقاومتی

در یک مدار که شامل یک باتری و یک مقاومت است می توانیم به راحتی هر کمیتی را محاسبه کنیم زیرا همه اجزای مدار از طریق دو نقطه به یکدیگر متصل هستند.

$$\large \begin{array}{l} I=\frac{V}{R} \\ I=\frac{9 \text { volts }}{3 \mathrm{k} \Omega}=3 \mathrm{~mA} \end{array}$$

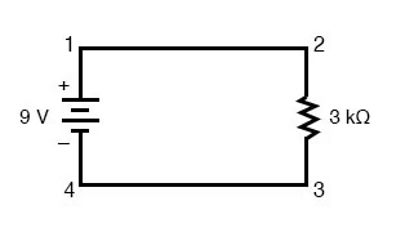
از آنجا که نقاط 1 و 2 مانند نقاط 3 و 4 توسط یک سیم که دارای مقاومت ناچیز است به هم متصل شده‌اند می‌توان گفت که نقطه 1 از نظر الکتریکی با نقطه 2 مشترک است و نقطه 3 از نظر الکتریکی با نقطه 4 مشترک است.

از طرفی می‌دانیم 9 ولت نیروی الکتریکی بین نقاط 1 و 4 (مستقیم از طریق باتری) برقرار است و از آنجا که نقطه 2 با نقطه 1 و نقطه 3 با نقطه 4 در ارتباط است، در نتیجه باید 9 ولت نیروی الکتریکی نیز بین نقاط 2 و 3 داشته باشیم.

بنابراین می‌توانیم بر اساس قانون اهم یعنی $$I=\frac{V}{R}$$ جریان الکتریکی را در دو سر مقاومت محاسبه کنیم.

استفاده از قانون اهم در مدارهای متوالی یا سری دارای چند مقاومت

در مدارهای حاوی بیش از یک مقاومت باید در نحوه استفاده از قانون اهم دقت کنیم. در مدار نمایش داده شده در تصویر (3) سه مقاومت داریم و می‌دانیم که 9 ولت نیروی محرکه الکتریکی باطری بین نقاط 1 و 4 وجود دارد و جریان را از طریق ترکیب سری مقاومت‌های $$R_{1}$$، $$R_{2}$$ و $$R_{3}$$ هدایت می‌کند. با این حال نمی‌توانیم مقدار 9 ولت را برای هر سه مقاومت در نظر بگیریم و باید آن را بر مقاومت‌های 3، 5 و 10 کیلواهمی تقسیم کنیم تا مقدار نیروی الکتریکی دو سر هر مقاومت را به دست آوریم. در نتیجه با توجه به اینکه می‌دانیم جریان در کل یک مدار متوالی یا سری یکسان است با محاسبه جریان می‌توانیم ولتاژ دو سر هر یک از مقاومت‌ها را نیز به دست آوریم.

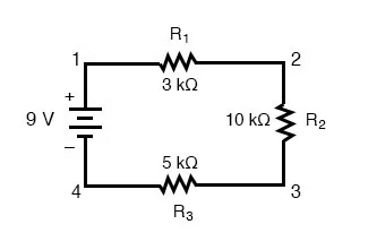
ولتاژ 9 ولت یک مقدار کل برای کل مدار است در حالی که مقاومت‌های 10، 3 و 5 کیلواهمی مقادیر منفرد برای هر یک از مقاومت‌های موجود در مدار است.

اگر بخواهیم یک ولتاژ برای هر یک از مقاومت‌ها بیان کنیم، روشن است که 9 ولت ولتاژ دقیق هیچ یک از مقاومت‌های داخل مدار نیست. این ولتاژ مربوط به کل مدار است و باید ولتاژ دو سر هر یک از مقاومت‌ها را محاسبه کنیم.

برای مقاومت $$R_{1}$$ با استفاده از قانون اهم می‌توانیم جریانی که از این مقاومت عبور می‌کند را محاسبه کنیم و داریم:

$$\large \mathrm{I}_{\mathrm{R} 1}=\frac{\mathrm{V}_{\mathrm{R} 1}}{3 \mathrm{k} \Omega} \quad \mathrm{E}_{\mathrm{R} 1}=I_{\mathrm{R} 1}(3 \mathrm{k} \Omega)$$

در رابطه بالا به وضوح می‌توان دید که استفاده از رابطه اهم برای مقاومت $$R_{1}$$ امکان پذیر نیست زیرا دو پارامتر مجهول جریان و انرژی الکتریکی داریم. این موضوع برای مقاومت‌های $$R_{2}$$ و $$R_{3}$$ نیز صدق می‌کند. به این ترتیب برای محاسبه جریان در مدار باید مقاومت کل مدار را به دست آوریم و سپس از قانون اهم استفاده کنیم تا جریان را به دست آوریم. بدین ترتیب به دومین اصل مدار متوالی یا سری می‌رسیم که مقاومت کل در یک مدار متوالی که شامل چندین مقاومت است برابر با حاصل جمع مقاومت‌های مدار است.

ترکیب چند مقاومت در یک مدار متوالی یا سری

همان طور که گفتیم دومین اصل مدارهای سری به صورت زیر است:

مقاومت کل یک مدار متوالی یا سری برابر با مجموع هر یک از مقاومت‌ها است. از لحاظ شهودی این مفهوم بدان معنا است که هر چه مقاومت‌های متوالی یا سری بیشتری در مسیر جریان قرار بگیرند، جریان الکتریکی با سختی بیشتری از این مقاومت‌ها عبور کرده و جریان می‌یابد.

در مسئله عنوان شده در تصویر (3)، یک مقاومت 3 کیلواهمی، 10 کیلواهمی و 5 کیلواهمی داریم و بر اساس اصل دوم مدار متوالی یا سری مقاومت کل این مدار برابر با 18 کیلواهم است:

$$\large \begin{array}{l} R_{\text {total }}=R_{1}+R_{2}+R_{3} \\ R_{\text {total }}=3 \mathrm{k} \Omega+10 \mathrm{k} \Omega+5 \mathrm{k} \Omega \\ \mathrm{R}_{\text {total }}=18 \mathrm{k} \Omega \end{array}$$

در واقع مقاومت معادل سه مقاومت موجود در مدار را که به صورت سری قرار گرفته بودند را به دست آوردیم و مدار معادل به صورت زیر رسم می‌شود:

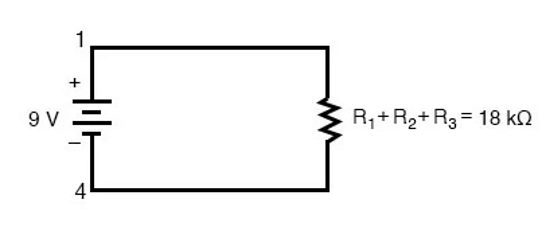
حال با دانستن مقاومت معادل و نیروی الکتریکی باطری می‌توان جریان را در مدار محاسبه کرد.

محاسبه جریان در مدار متوالی یا سری با استفاده از قانون اهم

اکنون همه اطلاعات لازم برای محاسبه جریان مدار مورد بحث را داریم زیرا ولتاژ بین نقاط 1 و 4، 9 ولت و مقاومت بین نقاط 1 و 4، 18 کیلواهم است و در نتیجه داریم:

$$\large \begin{array}{l} \mathrm{I}_{\text {total }}=\frac{\mathrm{V}_{\text {total }}}{\mathrm{R}_{\text {total }}} \\ \mathrm{I}_{\text {total }}=\frac{9 \text { volts }}{18 \mathrm{k} \Omega}=500 \mu \mathrm{A} \end{array}$$

محاسبه ولتاژ هر یک از مولفه‌های یک مدار متوالی یا سری با استفاده از قانون اهم

با دانستن اینکه جریان عبوری تمام اجزای یک مدار سری با یکدیگر برابر است می‌توانیم به مدار اصلی خود برگردیم و ولتاژ دو سر هر یک از مقاومت‌ها را با توجه به این که جریان در مدار متوالی ثابت است به دست آوریم:

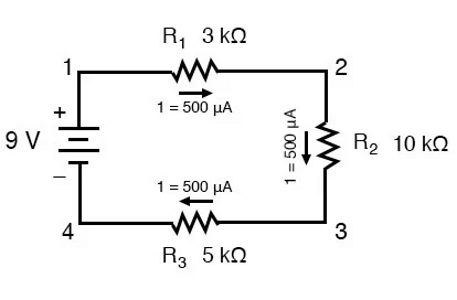
اکنون که میزان جریان هر مقاومت را می‌دانیم، می‌توانیم از قانون اهم برای تعیین افت ولتاژ در هر مقاومت استفاده کنیم:

$$\large \begin{array}{l} \mathrm{E}_{\mathrm{R} 1}=\mathrm{l}_{\mathrm{R} 1} \mathrm{R}_{1} \quad \mathrm{E}_{\mathrm{R} 2}=\mathrm{I}_{\mathrm{R} 2} \mathrm{R}_{2} \quad \mathrm{E}_{\mathrm{R3}}=\mathrm{l}_{\mathrm{R} 3} \mathrm{R}_{3} \\ \mathrm{E}_{\mathrm{R} 1}=(500 \mu \mathrm{A})(3 \mathrm{k} \Omega)=1.5 \mathrm{~V} \\ \mathrm{E}_{\mathrm{R} 2}=(500 \mu \mathrm{A})(10 \mathrm{k} \Omega)=5 \mathrm{~V} \\ \mathrm{E}_{\mathrm{R} 3}=(500 \mu \mathrm{A})(5 \mathrm{k} \Omega)=2.5 \mathrm{~V} \end{array}$$

به افت ولتاژ روی هر مقاومت توجه کنید و اینکه چگونه مقدار ولتاژ (1/5 + 5 + 2/5) برابر با ولتاژ باتری یا منبع تغذیه و برابر با 9 ولت است. این سومین اصل مدارهای متوالی یا سری است که بیان می‌کند ولتاژ منبع تغذیه در مدار متوالی یا سری برابر با جمع افت ولتاژ منفرد دو سر هر یک از مقاومت‌ها است.

برای آشنایی بیشتر با ترکیب مقاومت‌ها به صورت متوالی یا سری مطلب مقاومت سری در مدار — به زبان ساده را مطالعه کنید.

تجزیه و تحلیل مدارهای متوالی یا سری ساده با استفاده از روش جدول و قانون اهم

با این حال روشی که ما برای تحلیل این مدار متوالی یا سری استفاده کردیم، می‌تواند برای درک بهتر ساده‌تر نیز شود. از یک جدول برای لیست کردن تمام ولتاژها، جریان‌ها و مقاومت در مدار استفاده می‌کنیم که این روش می‌تواند تحلیل مدار را بسیار آسان‌تر کند. بدین ترتیب برای مدار مورد بحث در تصویر (3) داریم:

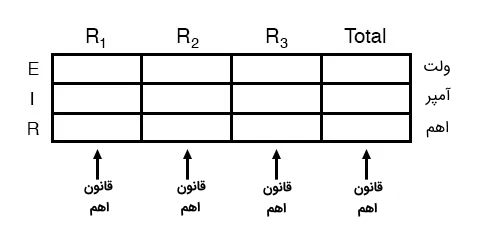
قانون اهم برای چنین جدولی در هر ستون اعمال می‌شود، به عنوان مثال $$E_{R1}$$ فقط برای $$I_{R1}$$ و $$R_{1}$$ یا $$E_{R2}$$ فقط برای $$I_{R2}$$ و $$R_{2}$$ و غیره. بدین ترتیب می‌توانیم تجزیه و تحلیل خود را برای این مدار آغاز کنیم.

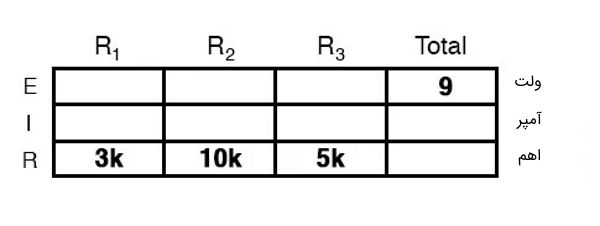
همانطور که پیش‌تر نیز گفته شده نمی‌توان نیروی محرکه الکتریکی 9 ولتی باطری را برای هر یک از مقاومت‌ها به کار برد. اما می‌توان از قانون مقاومت معادل برای مدار متوالی استفاده کرد و بدین ترتیب نیروی محرکه کل را برای مقاومت معادل به کار برد. براساس قانون مقاومت در مدار متوالی، مقاومت معادل برابر با مجموع مقاومت‌ها است و در نتیجه داریم:

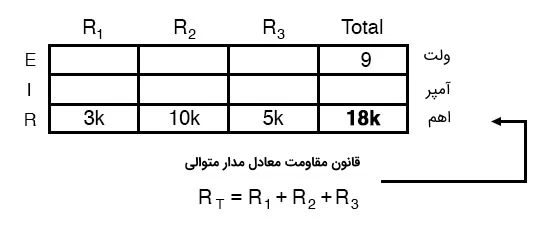
اکنون و با استفاده از قانون اهم می‌توان مقدار جریان را در ستون آخر این جدول محاسبه کرد. بدین ترتیب با استفاده از رابطه $$I=\frac{E}{R}$$ مقدار جریان برابر با 500 میکروآمپر به دست می‌آید و در جدول قرار می‌گیرد:

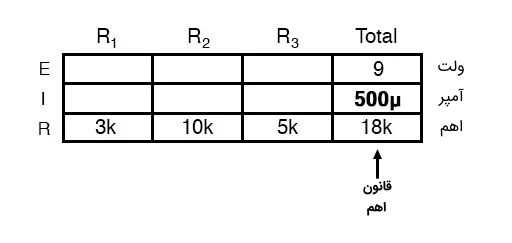
سپس با دانستن اینکه جریان به طور مساوی توسط تمام اجزای مدار متوالی تقسیم می‌شود (اصل دوم از اصول مدار متوالی یا سری) می‌توان جریان هر مقاومت را برابر با جریان مقاومت معادل در جدول یادداشت کرد و داریم:

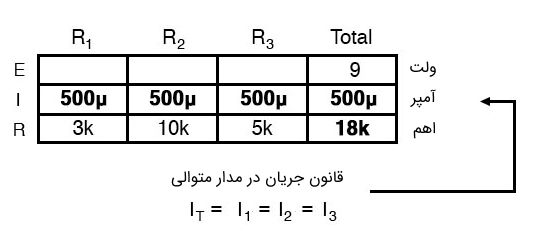
سرانجام می‌توانیم از قانون اهم برای تعیین افت ولتاژ در هر مقاومت در هر ستون استفاد کنیم و داریم:

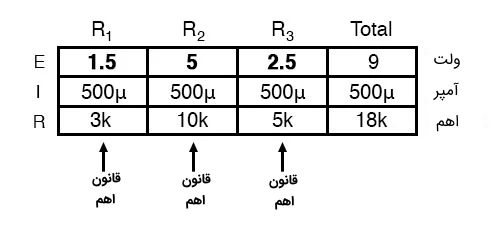
اتصال سری یا متوالی خازن

تصویر (6-الف) اتصال متوالی سه خازن را به منبع تغذیه نشان می‌دهد. همانطور که می‌دانید برای هر خازن ظرفیت خازن به بار الکتریکی و ولتاژ آن بستگی دارد و داریم:

$$\large C=\frac{Q}{V}$$

دقت کنید که در تصویر (6) هنگامی که ولتاژ V اعمال می‌شود، بار Q با مقداری برابر و علامتی مخالف به هر دو صفحه خازن بدون بار جریان می‌یابد. اصل پایستگی بار الکتریکی مستلزم ایجاد بارهایی با اندازه برابر در صفحات خازن‌های منفرد است زیرا بار فقط در این دستگاه‌های اصلی و خنثی جدا می‌شوند. نتیجه نهایی این مدار این است که این ترکیب شبیه یک خازن منفرد عمل می‌کند که بارهای مثبت و منفی را در فاصله بیشتری از هم جدا می‌کند (تصویر 6-ب).

جداسازی بیشتر بارهای مثبت و منفی به معنای ظرفیت کمتر است. این ویژگی کلی اتصالات متوالی خازن‌ها است که ظرفیت کل کمتر از ظرفیت خازن‌ها به صورت منفرد است.

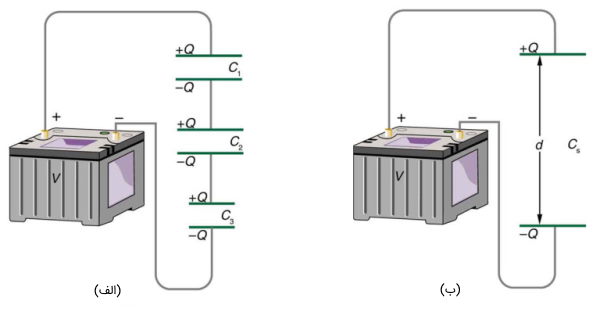
می‌توانیم با در نظر گرفتن ولتاژ روی خازن‌های منفرد که در تصویر (6) نشان داده شده است عبارتی برای ظرفیت خازن معادل پیدا کنیم و در حقیقت داریم:

$$\large C=\frac{Q}{V}$$

و در نتیجه برای ولتاژ نیز خواهیم داشت:

$$\large V=\frac{Q}{C}$$

بدین ترتیب ولتاژ روی هر یک از خازن‌ها نیز برابر است با:

$$\large V_1=\frac{Q}{C_1}$$
$$\large V_2=\frac{Q}{C_2}$$
$$\large V_3=\frac{Q}{C_3}$$

و ولتاژ کل نیز برابر با مجموع ولتاژهای منفرد است:

$$\large V=V_1+V_2+V_3$$

حال اگر ظرفیت خازن معادل خازن‌های سری را $$C_{s}$$ بنامیم، داریم:

$$\large V=\frac{Q}{C_s}=V_1+V_2+V_3$$

با قرار دادن مقادیر $$V_1$$، $$V_2$$ و $$V_3$$ در رابطه بالا، معادله به شکل زیر در می‌آید:

$$\large \frac{Q}{C_s}=\frac{Q}{C_1}+\frac{Q}{C_2}+\frac{Q}{C_3}$$

با حذف Q از طرفین معادله، ظرفیت کل مجموعه یا $$C_s$$ به شکل زیر به دست می‌آید:

$$\large \frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots$$

که در رابطه بالا علامت ... نشان می‌دهد که این عبارت برای هر تعداد خازن متصل به صورت متوالی معتبر است. در حقیقت باید بیان کرد که ترکیب هر تعداد خازن به صورت سری معادل با خازنی است که ظرفیت آن از ظرفیت هر یک از خازن‌های منفرد، همانطور که در تصویر (6) نیز نشان داده شده کمتر است.

پرسش: ظرفیت کل سه خازن متصل به صورت سری را با توجه به ظرفیت‌های 1، 5 و 8 میکروفارادی به دست آورید.

پاسخ: با استفاده از اطلاعات داده شده می‌توان ظرفیت خازن معادل را با استفاده از معادله ظرفیت خازن‌های به صورت متوالی یا سری به دست آورد، بدین ترتیب داریم:

$$\large \frac{1}{C_{\text{S}}}=\frac{1}{1.000 \mu\text{F}}+\frac{1}{5.000 \mu\text{F}}+\frac{1}{8.000 \mu\text{F}}=\frac{1.325}{\mu\text{F}}$$

و بدین تریب ظرفیت معادل به صورت زیر به دست می‌آید:

$$\large C_{\text{S}}=\frac{1.325}{\mu\text{F}}=0.755\mu\text{F}$$

خازن در مدار متوالی یا سری

همانطور که گفته شده در اتصال خازن‌ها به صورت متوالی یا سری، ظرفیت خازن معادل کمتر از ظرفیت هر یک از خازن‌ها به صورت منفرد است. بدین ترتیب در یک مدار متوالی یا سری با به دست آوردن ظرفیت خازن معادل در کل مدار و با داشتن مقدار نیروی محرکه الکتریکی باطری می‌توان بار کل را به دست آورد.

با به دست آمدن Q یا بار کل می‌توان ولتاژ را در دو سر هر یک از خازن‌ها به دست آورد. برای آشنایی بیشتر با ترکیب خازن‌ها به صورت سری یا متوالی مطلب خازن سری — به زبان ساده را مطالعه کنید.

سلف یا القاگر

سلف یا القاگر یک عنصر تاثیر پذیر است که در مدارهای الکترونیکی برای ذخیره موقت انرژی الکتریکی به شکل شار مغناطیسی یا به بیان ساده میدان مغناطیسی استفاده می‌شود. القا خاصیت هر سیم پیچ است که می‌تواند شار مغناطیسی را هنگام عبور جریان از آن تنظیم کند.

هر وسیله‌ای که خاصیت القایی داشته باشد را می‌توان سلف یا القاگر نامید. معمولاً سلف یا القاگر به شکل سیم پیچی از مواد مسی در اطراف هسته یک ماده مغناطیسی (آهن) یا غیر مغناطیسی (مانند هوا) ساخته می‌شود.

سلف‌ها ممکن است به صورت سری یا موازی به عملکرد مورد نیاز مدار وابسته باشند. از این ترکیبات برای طراحی شبکه‌های پیچیده‌تر استفاده می‌شود. اندوکتانس کل مدار به نحوه اتصال سلف‌ها به صورت متوالی یا موازی بستگی دارد.

علاوه بر این نحوه اتصال سلف‌ها به گونه‌ای است که یک القاگر هیچ تاثیری بر القای القاگر دیگر ندارد اما در مقایسه با اثر جفت مغناطیسی بین سلف‌ها، سلف کل را تغییر می‌دهد. در ادامه اتصال القاگرها به صورت متوالی یا سری را بررسی می‌کنیم.

اتصال سلف‌ها در مدار متوالی یا سری

فرض کنید بین سلف‌های متصل در یک مدار هیچگونه جفت شدگی وجود نداشته باشد. این بدان معنی است که هیچ خط شار از یک سلف متصل به دیگری وجود ندارد و از این رو هیچ شار متقابل بین سیم پیچ‌ها وجود نخواهد داشت.

اتصال انتها به انتهای دو یا چند سلف را اتصال متوالی یا سری سلف‌ها می‌نامند. در این اتصال سلف‌ها به صورت متوالی یا سری متصل می‌شوند بنابراین تعداد دورهای موثر سلف‌ها افزایش می‌یابد. اتصال متوالی یا سری سلف‌ها در تصویر زیر نشان داده شده است.

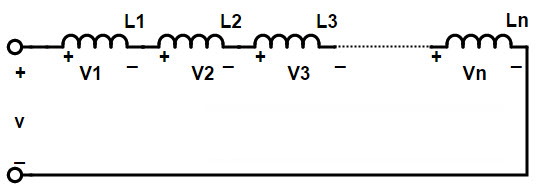
القای سلف‌های متصل به صورت متوالی یا سری به عنوان مجموع القاهای منفرد هر سیم پیچ محاسبه می‌شود زیرا جریان از هر سیم پیچ در یک مدار متوالی یا سری یکسان است.

این اتصال متوالی یا سری مشابه مقاومت‌های متصل به صورت سری است به جز اینکه مقاومت‌ها با سلف جایگزین شده‌اند. اگر جریان I در اتصال سری در مدار جریان داشته باشد و سیم پیچ‌ها $$L_1$$، $$L_2$$ و غیره باشند جریان در سلف‌های متوالی یا سری برابر و به صورت زیر است:

$$\large I_{\text {Total}}=I_{L 1}=I_{L 2}=I_{L 3} \ldots=I_{n}$$

اگر ولتاژ جداگانه روی هر سیم پیچ در این اتصال متوالی به ترتیب $$V_{L1}$$، $$V_{L2}$$ و غیره باشد، ولتاژ کل در این مدار برابر است با:

$$\large V_{\text {Total }}=V_{L 1}+V_{L 2}+V_{L 3 \cdots}+V_{n}$$

همانطور که می‌دانیم افت ولتاژ را می‌توان با خود القایی یا L نشان داد و بدین ترتیب داریم:

$$\large V=L\frac{di}{dt}$$

بنابراین داریم:

$$\large \mathrm{L_T} \mathrm{di} / \mathrm{dt}=\mathrm{L_1} \mathrm{di} / \mathrm{dt}+\mathrm{L_2} \mathrm{di} / \mathrm{dt}+\mathrm{L_3} \mathrm{di} / \mathrm{dt}+\ldots+\mathrm{L_n} \mathrm{di} / \mathrm{dt}$$

و القای کل در اتصال متوالی یا سری چندین القاگر برابر است با:

$$\large \mathrm{L}_{\text {Total }}=\mathrm{L}_{1}+\mathrm{L}_{2}+\mathrm{L}_{3}+\ldots \ldots+\mathrm{L}_{\mathrm{n}}$$

این بدان معنی است که القای کل در اتصال متوالی یا سری القاگرها برابر با مجموع القاهای هر یک از سلف‌ها است. دقت کنید که معادله فوق زمانی درست است که هیچ تأثیر القایی متقابل بین سیم پیچ‌ها در این پیکربندی متوالی یا سری وجود نداشته باشد.

القای متقابل سلف‌ها باعث تغییر در مقدار القای کل در ترکیب متوالی یا سری سلف‌ها خواهد شد. فرض کنید دو سلف به طور سری به یک منبع ولتاژ متناوب متصل شده‌اند که می‌توانند تغییرات جریان را در مدار ایجاد کنند، این موضوع در تصویر (7) نمایش داده شده است. بدین ترتیب اگر هیچ القایی متقابلی در مدار وجود نداشته باشد اندوکتانس کل برابر است با:

$$\large L_{T}=L_{1}+L_{2}$$

لازم به یادآوری است که القای کل در اتصال متوالی یا سری همیشه بیشتر از القای بزرگترین سلف در چینش سری سلف‌ها است. برای آشنایی بیشتر با اتصال سری سلف‌ها یا القاگرها مطلب اتصال سری سلف ها — به زبان ساده را مطالعه کنید.

پرسش: اگر یک مدار دارای 3 سلف 60، 30 و 20 هنری باشد که این سلف‌ها به صورت سری به یکدیگر متصل باشند، القای کل در این مجموعه چقدر خواهد بود؟

پاسخ: ما می دانیم که رابطه القای معادل در اتصال متوالی یا سری به صورت $$\mathrm{L}_{\text {Total }}=\mathrm{L}_{1}+\mathrm{L}_{2}+\mathrm{L}_{3}+\ldots \ldots+\mathrm{L}_{n}$$ است. اگر $$L_1=60$$، $$L_2=30$$ و $$L_3=20$$ هنری باشد، القای کل در این مدار برابر با 110 هنری خواهد بود.

مرور کلی

• اجزای موجود در یک مدار متوالی یا سری مقدار جریان یکسانی دارند یعنی $$I_{total}=I_1=I_2=I_3 \cdots$$
• مقاومت کل در یک مدار متوالی یا سری برابر با مجموع مقاومت‌ها است و داریم $$R_{total}=R_1+R_2+R_3+ \cdots$$
• ولتاژ کل در یک مدار سری برابر است با جمع افت ولتاژ منفرد در دو سر هر یک از اجزای مدار یعنی: $$V_{total}=V_1+V_2+V_3+ \cdots$$
• ظرفیت کل در یک مدار متوالی یا سری برابر با $$\frac{1}{C_{\text{S}}}=\frac{1}{C_{1}}+\frac{1}{C_{2}}+\frac{1}{C_{3}}+\dots$$ است.
• در اتصال متوالی یا سری القاگرها، القای کل برابر با $$\mathrm{L}_{\text {Total }}=\mathrm{L}_{1}+\mathrm{L}_{2}+\mathrm{L}_{3}+\ldots \ldots+\mathrm{L}_{n}$$ است.

جمع بندی

در این مطلب در مورد مدارهای متوالی صحبت کردیم و قوانین مربوط به ولتاژ، مقاومت، خازن، جریان و القاگر را در قرار گرفتن در یک مدار به صورت متوالی یا سری مورد بررسی قرار دادیم.