فیلتر کالمن بی اثر (UKF) – از صفر تا صد

زمانی که پیچیدگی یک سیستم دینامیک افزایش یابد، احتمال دارد «فیلتر کالمن توسعه یافته» (Extended Kalman Filter) یا EKF همگرا نشود و یا پیاده سازی آن بسیار دشوار شود. علاوه بر این، مرحله خطی‌سازی شامل محاسبه مشتقات جزئی در هر گام تکرار فیلتر است. این عوامل فیلتر کالمن توسعه یافته را به یک الگوریتم با هزینه محاسباتی بالا تبدیل می‌کنند. فیلتر کالمن بی اثر یا خنثی (Unscented Kalman Filter) یا به اختصار UKF برای رفع این مشکلات و بهبود عملکرد EKF، به عنوان جایگزینی مناسب به وجود آمده است.

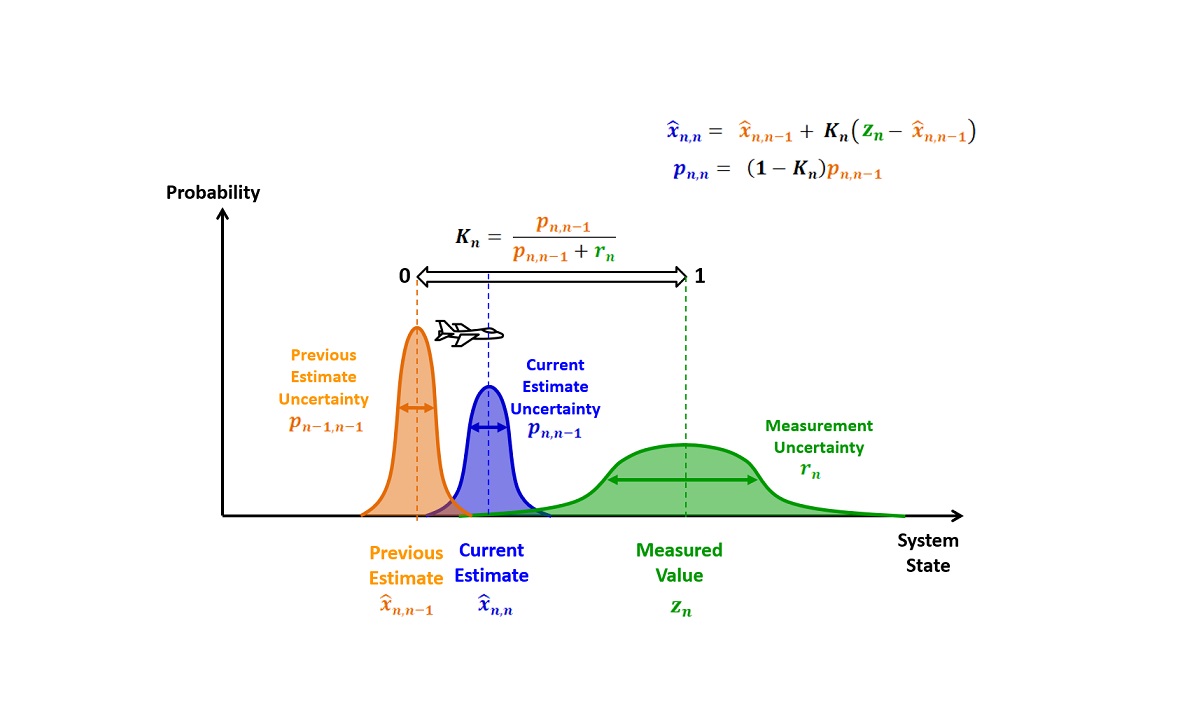
فیلتر کالمن بی اثر یا خنثی به کلاس بزرگی از فیلترها تعلق دارد که «فیلتر کالمن نقطه سیگما» (Sigma-Point Kalman Filters) یا «رگرسیون خطی» (Linear Regression) نام دارند. این کلاس از فیلترها از تکنیک‌های «خطی سازی آماری» (Statistical Linearization) استفاده می‌کنند. این تکنیک‌ها برای خطی سازی یک تابع غیرخطی از یک متغیر تصادفی به کار گرفته می‌شوند که از یک رگرسیون خطی بین n نقطه کشیده شده از توزیع‌های پیشین متغیرهای تصادفی استفاده می‌کنند. به این دلیل که در این تکنیک گستره متغیرهای تصادفی را در نظر می‌گیریم، در نتیجه نسبت به خطی سازی سری تیلور از دقت بالاتری برخوردار است. در این مطلب قصد داریم به بررسی فیلتر کالمن بی اثر یا خنثی بپردازیم و نحوه عملکرد آن را بیان کنیم.

فیلتر کالمن بی اثر

در فیلتر کالمن توسعه یافته، توزیع حالت‌ها به صورت تحلیلی از طریق خطی سازی مرتبه اول سیستم غیرخطی انتشار می‌یابد که به این دلیل «میانگین پسین» (Posterior Mean) و کواریانس می‌توانند خراب شوند. به عبارت دیگر، در فیلتر کالمن توسعه یافته، زمانی که گذار حالت‌ها و مدل‌های تخمین‌گر (برای پیش‌بینی و آپدیت حالت‌ها) به شدت غیرخطی باشند، عملکرد فیلتر EKF بسیار ضعیف خواهد بود؛ زیرا کواریانس از طریق خطی سازی مدل غیرخطی اصلی انتشار می‌یابد.

فیلتر کالمن بی اثر یا UKF یک نمونه مشتق گرفته شده از EKF است که این مشکل را حل می‌کند. در فیلتر کالمن خنثی از یک روش «نمونه‌برداری قطعی» (Deterministic Sampling) استفاده می‌شود. توزیع حالت‌ها با استفاده از مجموعه کمینه نقاط نمونه نمایش داده می‌شود که با دقت بالایی انتخاب شده‌اند. این نقاط را «سیگما پوینت» (Sigma Point) می‌گویند. همانند فیلتر EKF، فیلتر UKF نیز شامل دو گام اساسی است. این دو گام «پیش‌بینی مدل» (Model Forecast) و «ادغام داده» (Data Assimilation) نام دارند.

الگوریتم فیلتر کالمن بی اثر بر این اصل استوار شده است که تخمین زدن توزیع احتمالاتی آسان‌تر از تخمین یک تابع یا یک تبدیل غیرخطی تصادفی است. نقاط سیگما در فیلتر کالمن بی اثر به صورتی انتخاب می‌شوند که میانگین و کواریانس آن‌ها دقیقا برابر با $$X ^ a _ { K - 1 }$$ و $$\bf { P } _ { k - 1 }$$ باشد. سپس هر نقطه سیگما از طریق غیرخطی حاصل از انتهای ابر نقاط تبدیل شده، منتشر می‌شود. میانگین و کواریانس جدید تخمین زده شده بر اساس ویژگی‌های آماری آن‌ها محاسبه می‌شوند. به این فرایند فیلتر کالمن بی اثر می‌گویند. «تبدیل بی اثر» (Unscented Transformation) نیز نام یک روش برای محاسبه احتمال یک متغیر تصادفی تحت یک تابع غیرخطی است.

تبدیل بی اثر

همان طور که گفتیم، اساس فیلتر کالمن بی اثر بر یک فرایند استوار است که به آن تبدیل بی اثر می‌گویند. در این فرایند، مجموعه نقاط سیگما پوینت از تابع غیرخطی سیستم عبور داده می‌شوند تا مقادیر میانگین و کواریانس مربوط به توزیع حالت‌های جدید به دست آیند. در نتیجه می‌توان نوشت:

$$y _ { \sigma } = f ( \chi )$$

در رابطه فوق، $$y _ { \sigma }$$ یک تابع از ماتریس نقاط سیگما است که با $$\chi$$ نشان داده شده است. این رابطه منجر به ایجاد یک ماتریس دیگر می‌شود که شامل نقاط سیگما تبدیل یافته‌ای می‌شود که از تابع غیرخطی عبور داده شده‌اند. با استفاده از رابطه فوق می‌توان توزیع حالت گاوسی مربوط به حالت‌های تخمینی را تقریب زد. به کل این فرایند تبدیل بی اثر می‌گویند. نمایش گرافیکی از تخمین گاوسی توزیع حالت‌ها قبل و بعد از تبدیل بی اثر در تصویر زیر نشان داده شده است.

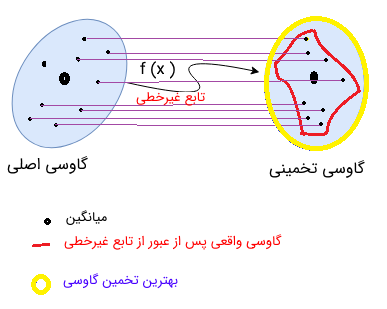
گام‌های اساسی برای پیاده‌سازی فیلتر کالمن بی اثر به ترتیب زیر است:

فیلم آموزش کنترل بهینه – جامع و با مفاهیم کلیدی در فرادرس

کلیک کنید

1. محاسبه مجموعه نقاط سیگما
2. تخصیص وزن‌های هر سیگما پوینت
3. تبدیل نقاط سیگما با استفاده از تابع غیر خطی
4. محاسبه توزیع گاوسی حالت‌های جدید و وزن‌های متناظر با آن
5. یافتن میانگین و واریانس توزیع گاوسی جدید

نقاط سیگما

برای تبدیل بی اثر، یک مجموعه از نقاط نمونه مقیاس شده (Scaled) محاسبه می‌شود که به آن‌ها نقاط سیگما می‌گویند. در واقع نقاط سیگما یک مجموعه کمینه از نقاط با دقت انتخاب شده هستند که به صورت تقریبی توزیع گاوسی سیستم غیرخطی را مدل می‌کنند. زمانی که این نقاط از تابع غیرخطی عبور داده می‌شوند، این توانایی را دارند که انتشار خطا و حالت را مدل کنند و این کار را با دقت بسیار بیشتری نسبت به تخمین فیلتر کالمن توسعه یافته انجام می‌دهند.

سیگما پوینت‌ها را می‌توان با استفاده از الگوریتم «Van der Merwe» محاسبه کرد. این الگوریتم فقط با استفاده از سه پارامتر $$\alpha$$ و $$\beta$$ و $$\kappa$$ یک مجموعه توزیع شده وزن‌دار و مقیاس شده از نقاط سیگما را محاسبه می‌کند که توزیع حالت‌ها را تخمین می‌زند. با استفاده از این الگوریتم، ماتریس سیگما پوینت‌ها یا $$\chi$$ با $$2 n + 1$$ ستون به دست می‌آید که n برابر با تعداد بعدهای سیستم در نظر گرفته شده است. نقطه اول یا $$\chi _ 0$$ برابر با مقدار میانگین ورودی است و سایر مقادیر به صورت زیر محاسبه می‌شوند:

$$\chi _ 0 = \mu$$

$$\chi _ { i } = \left\{ \begin {array} { l l } { \mu + [ \sqrt { ( n + \lambda ) \Sigma } ] _ { i } } & { \text { for } i = 1 \cdots n} \\ { \mu - [ \sqrt { ( n + \lambda ) \Sigma } ] _ { i - n } } & { \text { for } i = ( n + 1 ) \cdots 2 n} \end {array} \right.$$

که در رابطه بالا، $$\sqrt { ( n + \lambda ) \Sigma }$$ یک ماتریس است. اندیس i نشان دهنده بردار ستونی در این ماتریس است. $$\lambda = \alpha ^ 2 ( n + \kappa ) - n$$ و $$\alpha$$ و $$\kappa$$ پارامترهای مقیاس شده از توزیع نقاط سیگما و $$n$$ ابعاد حالت‌ها هستند. علاوه بر این، ریشه دوم ماتریس کواریانس $$\sum$$ که توسط فاکتور $$\lambda$$ مقیاس شده است را نیز محاسبه می‌کنیم و تقارن را با کم کردن و اضافه کردن آن به میانگین حفظ می‌کنیم. در نهایت ماتریس نقاط سیگما به صورت زیر به دست می‌آید:

$$\chi = \left[ \begin {array} { c c c c c } { \chi _ { 0 , 0 } } & { \chi _ { 0 , 1 } } & { \chi _ { 0 , 2 } } & { \cdots } & { \chi _ { 0 , 2 n + 1 } } \\ { \chi _ { 1 , 0 } } & { \chi _ { 1 , 1 } } & { \chi _ { 1 , 2 } } & { \cdots } & { \chi _ { 1 , 2 n + 1 } } \\ { \chi _ { 2 ,0 } } & { \chi _ { 2 , 1 } } & { \chi _ { 2 , 2 } } & { \cdots } & { \chi _ { 2 , 2 n + 1 } } \\ { \vdots } & { \vdots } & { \vdots } & { \ddots } & { \vdots } \\ { \chi _ { n - 1 , 0 } } & { \chi _ { n - 1 , 1 } } & { \chi _ { n - 1 , 2 } } & { \cdots } & { \chi _ { n - 1 , 2 n + 1 } } \end {array} \right]$$

محاسبه وزن‌ها

نقاط سیگما همچنین با استفاده از $$\lambda$$ به عنوان فاکتور مقیاس کننده، وزن‌دهی می‌شوند. مقدار وزن متناظر برای اولین مقدار میانگین $$\omega ^ m _ 0$$ با استفاده از معادله زیر محاسبه می‌شود:

$$\omega ^ m _ 0 = \frac { \lambda } { n + \lambda }$$

در این رابطه $$n$$ برابر با ابعاد سیستم و $$\lambda = \alpha ^ 2 ( n + \kappa ) - n$$ است. وزن‌های بقیه سیگما پوینت‌های $$\chi _ 1 , ... , \chi _ { 2 n + 1 }$$ با استفاده از رابطه زیر محاسبه می‌شود:

$$\omega ^ m _ i = \frac { 1 } { 2 ( n + \lambda ) } \; \; \; \; \; i = 1 , ..., 2n \\$$

در ادامه می‌بینیم که چگونه این نقاط سیگما و وزن‌ها با همکاری یکدیگر عمل می‌کنند و حالت‌های سیستم غیرخطی را در یک رشته متوالی تخمین و پیش‌بینی می‌کنند.

گام پیش‌بینی

«نقاط سیگما تبدیل شده» (Transformed Sigma Points) همراه با وزن‌ها برای پیش‌بینی حالت‌های پیشین و توزیع گاوسی کواریانس خطا مورد استفاده قرار می‌گیرد و برای این کار از معادله زیر استفاده می‌شود:

$$X _ k = \sum _ { i = 0 } ^ { 2 n } \omega ^ m _ i y _ \sigma$$

$$P _ k = \sum _ { i = 0 } ^ { 2 n } \omega ^ c _ i ( y _ \sigma - X _ k ) ( y _ \sigma - X _ k ) ^ T + Q$$

در این رابطه $$\omega ^ m$$ وزن‌های متناظر با مقادیر میانگین و $$\omega ^ c$$ وزن‌های متناظر با کواریانس خطای P هستند.

گام به‌روزرسانی

برای مرحله به‌روزرسانی یا آپدیت کردن، یک تابع اندازه‌گیری می‌سازیم که نقاط سیگما را به فضای اندازه‌گیری تبدیل کند و گام آپدیت کردن در فیلتر کالمن بی اثر انجام شود:

$$\mathbb { Z } = h ( y _ \sigma )$$

مجددا با استفاده از فیلتر کالمن بی اثر، سیگما پوینت‌ها و وزن‌های متناظر را به تابع اندازه‌گیری می‌دهیم تا حالت‌ها و کواریانس را در فضای اندازه‌گیری به صورت زیر محاسبه کند:

$$\begin {aligned} \mu _ { \mathbb { Z } _ { k } } & = \sum _ { i = 0 } ^ { 2 n } w _ { i } ^ { m } \mathbb { Z } \\ \mathrm { P } _ { \mathbb { Z } _ { k } } & = \sum _ { i = 0 } ^ { 2 n } w _ { i } ^ { c } \left ( \mathbb { Z } -\mu _ { z _ { k } } \right) \left (\mathbb { Z } -\mu _ { z _ { k } } \right) ^ { T } + \mathrm { R } \end{aligned}$$

حال باید مقادیر «مانده» (Residual) تخمین های حالت و مقادیر واقعی اندازه گیری را محاسبه کنیم. برای این کار باید از فرمول زیر استفاده کنیم:

$$\large Y = Z - \mu _ { zk }$$

در این رابطه، $$Z$$ نشان دهنده مقادیر اندازه‌گیری با استفاده از سنسور و $$\large \mu _ { zk }$$ نشان دهنده میانگین وزن‌دار نقاط سیگما تبدیل شده است.

بهره کالمن

بهره کالمن با استفاده از ماتریس «کواریانس متقاطع» (Cross Covariance) بین حالت‌ها و اندازه‌گیری‌ها محاسبه می‌شود. ماتریس کواریانس متقاطع بر اساس رابطه زیر به دست می‌آید:

$$\mathrm { P } _ { \mathrm { x z } } = \sum w _ { i } ^ { c } \left ( y _ { \sigma } - \mathrm { x } \right ) \left ( \mathbb { Z } - \mu _ { z } \right) ^ { T }$$

برای محاسبه بهره کالمن نیز از رابطه زیر استفاده می‌کنیم:

$$\mathrm { K } = \mathrm { P } _ { \mathrm { X Z } } \mathrm { P } _ { \mathbb { Z } } ^ { - 1 }$$

در نهایت باید مانده‌های وزن‌دار را برای محاسبه یک تخمین پسین از حالت $$\hat { \mathbf { x } } _ { k }$$ و کواریانس خطای صحیح $$\mathrm { P }$$ با روابط زیر به دست آوریم:

$$\begin {aligned} \hat { \mathbf { x } } _ { k } & = \mathrm { x } _ { k } + \mathrm { K } y \\ \hat { \mathrm { P } } _ { k } & = \mathrm { P } _ { k } -\mathrm { K P } _ { \mathrm { Z } } \mathrm { K } ^ { T } \end {aligned}$$

در این رابطه، $$\hat { \mathbf { x } }$$ تخمین صحیح از حالت $$x$$ و $$\hat { \mathrm { P } }$$ کواریانس خطای صحیح است.

فیلتر کالمن بی اثر در متلب

در ادامه کدنویسی الگوریتم UKF به دو صورت در نرم‌افزار متلب ارائه می‌شود. در برنامه اول با استفاده از دستورات پایه متلب و خط به خط برنامه‌نویسی انجام شده است و عملکرد الگوریتم برای تخمین حالت‌های دینامیک غیرخطی «وان در پول» (Van Der Pol) نیز مورد بررسی قرار گرفته است. در برنامه دوم نیز با استفاده از تولباکس‌های آماده نرم افزار متلب کدنویسی انجام شده است. برنامه اول برای افرادی که حوزه تحقیقاتی آنها در مورد خود الگوریتم UKF است مناسب است و برنامه دوم نیز برای محققینی که صرفا یک الگوریتم برای تخمین حالت سیستم‌های غیرخطی لازم دارند، قابل استفاده است.

فیلم آموزش کنترل مدرن و پیاده سازی در متلب MATLAB در فرادرس

کلیک کنید

معادلات دینامیکی سیستم غیرخطی وان در پول بصورت زیر تعریف می‌شوند. رفتار سیستم نوسانی و آشوبناک است و فرض می‌کنیم موقعیت اولیه ۲ و سرعت اولیه حالت نیز ۰ باشد:

$$\ddot { y ( t ) } + ( 1 - y ^ 2 ( t) ) \dot { y } + y ( t) = 0$$

در قدم اول باید سیستم را به فرم فضای حالت نوشت. متغیرهای حالت موقعیت و سرعت اولیه انتخاب می‌شوند. در نتیجه بیان فضای حالت سیستم و خروجی قابل‌اندازه‌گیری بصورت زیر خواهد بود:

$$\dot{ x ( t ) } = \begin {bmatrix} { x _ 2 ( t )} \\ { (1 - x _ 1 ^ 2 ( t) ) x _ 2 ( t ) + x _ 1 ( t ) } \end{bmatrix} = f ( x ( t ) ) \\ y ( t )= x _ 1 ( t ) = h ( x ( t ) )$$

در قدم بعد باید توجه کرد که الگوریتم UKF برای تخمین حالت سیستم‌های گسسته استفاده می‌شود. بنابراین با استفاده از تقریب اویلر برای مشتق می‌توان سیستم را به شکل زیر گسسته‌سازی کرد:

$$x ( t + 1 ) = x ( t ) + T _ s f ( x ( t ) )$$

$$T _ s$$ زمان نمونه‌برداری است و مقدار آن در شبیه‌سازی برابر با ۰٫۰۵ انتخاب می‌شود. طول بازه شبیه‌سازی نیز ۲۰ ثانیه درنظر گرفته می‌شود. همچنین باید توجه کرد که t در رابطه بالا بیانگر شماره نمونه است. دینامیک وان در پول و سیستم اندازه‌گیری آن در توابع زیر پیاده‌سازی شده‌اند:

الگوریتم تخمین حالت برای سیستم‌های غیرخطی توسط UKF نیز در تابع متلب زیر پیاده‌سازی شده است.

سپس در برنامه زیر تخمین حالت‌ سیستم غیرخطی تعریف‌ شده انجام خواهد شد.

با اجرای برنامه بالا شکل زیر رسم خواهد شد.

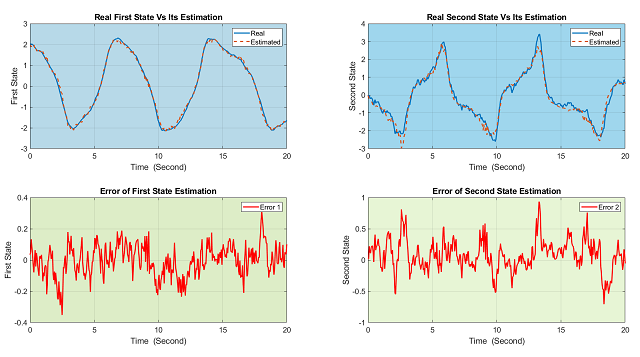
در گراف‌های بالا، نمودارهای آبی‌ رنگ حالت‌های واقعی سیستم هستند و نمودارهای قرمز‌ رنگ نیز تخمین آنها توسط الگوریتم UKF است. گراف‌های پایین نیز خطای بین حالت‌های واقعی سیستم و مقادیر تخمینی آنها را نشان می‌دهند. کاملا واضح است که عملکرد تخمینگر رضایت بخش‌ است و به خوبی توانسته است حالت‌های سیستم غیرخطی وان در پول را تخمین بزند. همچنین باید توجه کرد که در برنامه برای اینکه عملکرد الگوریتم تخمین‌گر با وضوح بیشتری نشان داده شود، نویز پروسه و نویز اندازه‌گیری مقادیر بزرگی در نظر گرفته شده است.

فیلتر کالمن بی اثر با استفاده از توابع آماده متلب

در حالت بعد الگوریتم UKF با استفاده از توابع آماده متلب پیاده‌سازی خواهد شد. با استفاده از دستور unscentedKalmanFilter فیلتر کالمن UKF ساخته خواهد شد. با دستور predict فاز پیش‌بینی و با دستور correct نیز فاز به‌روزرسانی‌ حالت‌های تخمین و ماتریس کواریانس انجام خواهد شد.

به منظور تخمین حالت توسط این توابع ابتدا همانند برنامه اول توابع دینامیک سیستم و اندازه‌گیری تعریف خواهد شد و سپس از برنامه زیر استفاده می‌کنیم.

با اجرای برنامه بالا شکل زیر رسم خواهد شد. نتایج مشابه برنامه اول است و نشانگر عملکرد فوق‌العاده الگوریتم تخمین حالت غیرخطی UKF برای سیستم‌های دینامیکی غیرخطی است.

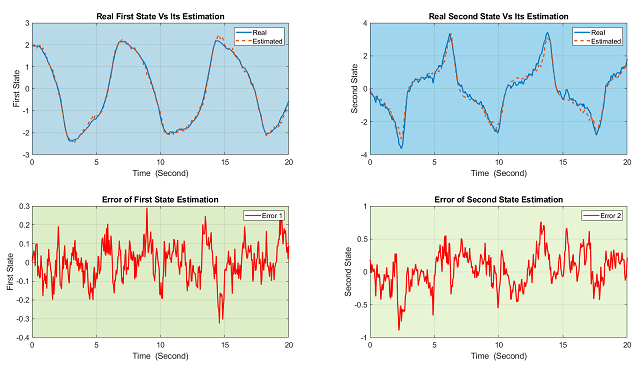
اگر این مطلب برای شما مفید بوده است، آموزش‌های زیر نیز به شما پیشنهاد می‌شوند:

• مجموعه آموزش‌های دروس مهندسی کنترل
• آموزش کنترل مدرن به همراه پیاده سازی در متلب​‎
• مجموعه آموزش‌های مهندسی برق
• آموزش کاربرد متلب در مهندسی کنترل
• فیلتر کالمن — به زبان ساده
• کنترل بهینه در متلب — از صفر تا صد
• کنترل پیش بین مدل (MPC) — راهنمای جامع

^^