ضرب کسرها – به زبان ساده + حل تمرین و مثال
در آموزشهای پیشین مجله فرادرس، با کسرها آشنا شدیم. همچنین، به مباحثی از قبیل تبدیل کسر به عدد اعشاری و تجزیه کسرها پرداختیم. ضرب کسرها، برخلاف جمع و تفریق آنها و حتی تقسیمشان، بسیار ساده است. در این آموزش، روش انجام ضرب کسرها را با کمک شکل، محور اعداد و عملیات ریاضی بیان خواهیم کرد. هم چنین، چند مثال را بررسی میکنیم.


کسر چیست؟
کسرها اعدادی هستند که با تقسیم دو عدد صحیح تعریف میشوند و برای نشان دادن هر تعداد از قسمتهای مساوی یک چیز بهکار میروند. آنها اعدادی حقیقی بهفرم هستند که در آنها و اعدادی صحیحاند. عدد صورت کسر و عدد مخرج کسر نامیده میشود. بنابراین، در کسر عدد ۲ صورت و عدد ۳ مخرج کسر است و آن را «دو سوم» میخوانیم.
در اینجا یک نمایش بصری از مفهوم کسر ارائه میکنیم. به شکل زیر دقت کنید که به سه قسمت مساوی تقسیم و دو قسمت آن آبی شده است. میگوییم دو سوم این شکل آبی است و آن را با نشان میدهیم.

در گامهای زیر میتوان به شکل بالا برای کسر رسید:
۱. ابتدا کل شکل که ۱ واحد است را رسم میکنیم.

۲. این یک واحد را طبق مخرج (عدد ۳) به سه قسمت مساوی تقسیم میکنیم (یعنی ).
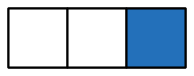
۳. نتیجه را در عدد صورت، یعنی ۲، ضرب میکنیم و به کسر میرسیم.
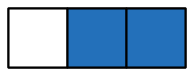
کسرها را میتوان به سه دسته تقسیم کرد:
- کسرهای سره که در آنها صورت از مخرج کوچکتر است، مثل
- کسرهای ناسره که در آنها صورت کسر از مخرج آن بزرگتر است، مانند .
- عدد مخلوط که بخشی از آن یک عدد صحیح و بخشی از آن یک کسر است. بخش کسری این عدد همواره یک کسر سره است.
برای آشنایی با اعداد مخلوط، میتوانید به آموزش «عدد مخلوط چیست و به چه اعدادی می گویند؟ — به زبان ساده» از مجله فرادرس مراجعه کنید.
ضرب کسرها با عملیات ریاضی
ضرب کسرها با عملیات ریاضی کار سادهای است. برای ضرب کسرها با عملیات ریاضی، صورتها را در هم و مخرجها را در هم ضرب میکنیم. برای مثال، اگر دو کسر و را داشته باشیم، حاصلضرب آنها بهصورت زیر خواهد بود:
برای مثال، برای ضرب ، خواهیم داشت:
که البته میتوان آن را سادهتر نیز کرد:
برای هر تعداد کسر که داشته باشیم، از همین قاعده پیروی میکنیم. برای مثل، برای ضرب زیر داریم:
ضرب عدد در کسر
ضرب عدد در کسر به شکل زیر است:
این ضرب را میتوان به سه شیوه انجام داد که در ادامه آنها را بیان میکنیم.
ضرب عدد در کسر با عملیات ریاضی
ضرب عدد در کسر با عملیات ریاضی ساده است. کافی است عدد را با قرار دادن عدد ۱ در مخرج به کسر تبدیل کنیم و مانند بخش قبل، صورت را در صورت و مخرج را در مخرج ضرب کنیم. فرض کنید میخواهیم ضرب زیر را انجام دهیم:
کافی است بهجای عدد ، کسر را قرار دهیم:
این عدد کسری را میتوانیم به یک عدد مخلوط تبدیل کنیم:
ضرب عدد در کسر با شکل
برای مثال، میخواهیم ضرب زیر را انجام دهیم:
این ضرب معادل این گفته است: چهار تا سهپنجم.
بنابراین، باید چهار تا شکل رسم کنیم. از آنجا که مخرج کسر است، باید شکلهایی با قسمت داشته باشیم. اکنون چهار تا را مشخص میکنیم.
شکلها در زیر نشان داده شدهاند.
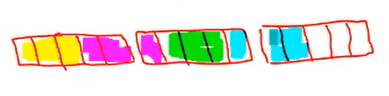
اکنون کافی است تعداد خانههای مشخص شده را بشماریم. میبینیم که خانه رنگی است. از آنجا که ارزش هر خانه برابر با است، بنابراین، را داریم و جواب است.
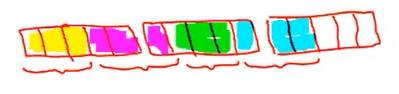
همانطور که میبینیم، صورت کسر از مخرج آن بزرگتر است (کسر ناسره است) و میتوانیم آن را به یک عدد مخلوط تبدیل کنیم.
این کار را بهصورت زیر انجام میدهیم:
ضرب عدد در کسر با محور اعداد
برای انجام ضرب کسرها روی محور، کافی است یک محور اعداد رسم کرده و اعداد را روی آن مشخص میکنیم. سپس هر واحد را به واحدهای کوچکتر تقسیم میکنیم. چون در اینجا مخرج است، هر واحد را به بخش تقسیم میکنیم. شکل زیر این موضوع را بهخوبی نشان میدهد.

اکنون برای انجام ضرب، باید چهار تا را مشخص کنیم. برای این کار، چهار عدد کمان را مشخص میکنیم. شکل زیر این موضوع را نشان میدهد.

نقطهای که به آن میرسیم، معادل است. در واقع، دو واحد کامل و دو تا از یکپنجمها داریم.
ضرب کسر در عدد
ضرب کسر در عدد به صورت زیر است:
با سه روش میتوانیم ضرب کسر در عدد را محاسبه کنیم که در ادامه به آنها میپردازیم.
ضرب کسر در عدد با عملیات ریاضی
ضرب کسر در عدد با عملیات ریاضی کار آسانی است. کافی است در مخرج عدد، عدد ۱ را قرار دهیم و صورت را در صورت و مخرج را در مخرج ضرب کنیم. برای مثال، فرض کنید میخواهیم ضرب زیر را انجام دهیم:
برای این کار، کافی است بهجای کسر را قرار دهیم:
ضرب کسر در عدد با شکل
برای مثال، فرض کنید میخواهیم حاصل ضرب زیر را محاسبه کنیم:
در اینجا، کل را داریم که عدد است و باید آن را محاسبه کنیم.
بدین منظور، شکل را رسم میکنیم. با توجه به مخرج، هر شکل باید سه قسمتی باشد. بنابراین، هر شکل را به سه قسمت تقسیم میکنیم. اکنون باید شش تا را مشخص کنیم. بدین منظور از هر شکل را مشخص میکنیم.

اکنون باید تعداد خانههای کوچکی را که رنگ کردهایم، بشماریم. میبینیم که تعداد آنها است. از آنجا که ارزش هر خانه کوچک است، پس جواب خواهد بود.
همانطور که میبینیم بر بخشپذیر است و میتوان نوشت:
ضرب کسر در عدد با محور اعداد
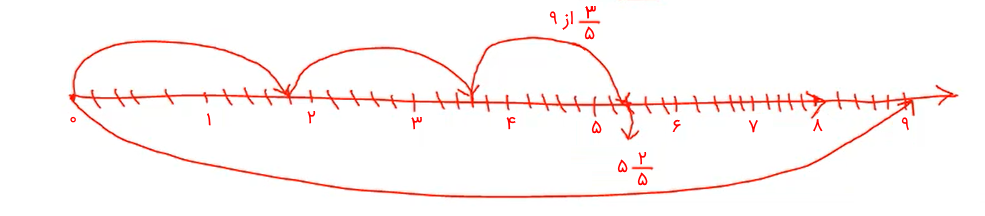
فرض کنید میخواهیم ضرب را انجام دهیم. برای این کار ابتدا 9 واحد را روی محور اعداد مشخص میکنیم. سپس، با توجه به اینکه مخرج کسر برابر با 5 است، هر واحد را به ۵ قسمت تقسیم میکنیم. تعداد خانههای کوچک تا است. باید این ۴۵ خانه را جدا کنیم. باید سه تا کمان تایی جدا کنیم. با شمردن خانهها میبینیم که ۲۷ خانه داریم و بنابراین، حاصلضرب برابر با است.
مثالهای ضرب کسرها
در این بخش، مثالهایی را از ضرب کسرها بررسی میکنیم.
مثال اول ضرب کسرها
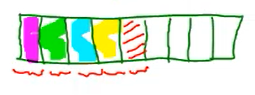
ضرب زیر را روی شکل نمایش دهید.
حل: از شکل شروع میکنیم. ابتدا شکلهای یکنهمی را رسم میکنیم. باید پنج تا از آنها را مشخص کنیم. همانطور که در شکل زیر مشخص شده است، از شکل رنگ شده و بنابراین، جواب است.
مثال دوم ضرب کسرها
ضرب زیر را روی محور نمایش دهید.
حل: از محور اعداد برای انجام ضرب کمک میگیریم. واحدهای با بخش را روی محور اعداد مشخص میکنیم. اکنون به کمک مشخص کردن کمانها، تا واحد را مشخص میکنیم. در واقع، کمان رسم میکنیم.

در نهایت، میبینیم که را داریم.
مثال سوم ضرب کسرها
ضرب زیر را با کمک شکل انجام دهید:
حل: برای این کار ابتدا ۹ شکل را رسم میکنیم. سپس هر کدام را به ۵ قسمت تقسیم میکنیم، زیرا مخرج کسری که در آن ضرب شده است، عدد ۵ است. سپس ۳ خانه از ۵ خانه هر شکل را رنگ میزنیم. در نهایت، تعداد خانههای کوچکی را که رنگ کردهایم میشماریم.

با شمردن بخشهای هاشورخورده، میبینیم که ۲۷ خانه داریم و بنابراین، حاصلضرب برابر با است.
مثال چهارم ضرب کسرها
ضرب کسری را انجام دهید.
حل: همانطور که گفتیم، صورت و مخرج را در یکدیگر ضرب میکنیم و خواهیم داشت:
از آنجا که بزرگترین مقسومعلیه مشترک بین دو عدد ۱۲ و ۱۸، عدد ۶ است، صورت و خرج را بر این دو عدد تقسیم میکنیم تا کسر ساده شود:
بنابراین، داریم:
اگر کسر یک کسر مخلوط باشد، ابتدا آن را به یک کسر ناسره تبدیل میکنیم، سپس ضرب را طبق مراحلی که پیشتر گفتیم انجام میدهیم. در ادامه، مثالی را از این مورد بررسی میکنیم.
مثال پنجم ضرب کسرها
حاصل ضرب را بهدست آورید.
حل: ابتدا دو کسر مخلوط را به کسرهای ناسره تبدیل میکنیم. بنابراین، داریم:
از آنجا که بزرگترین مقسومعلیه مشترک دو عدد و ، عدد است، جواب نهایی خواهد بود:
دقت کنید که کاری مانند زیر انجام ندهید:
در ادامه، یک مثال دیگر را بررسی میکنیم.
مثال ششم ضرب کسرها
عبارت زیر را ساده کنید:
حل: ابتدا کسر آمیخته را به یک کسر ناسره تبدیل میکنیم:
بنابراین، داریم:
مثال هفتم ضرب کسرها
حاصلضرب عبارت زیر را بهدست آورید:
حل: ابتدا کسر آمیخته را به یک کسر ناسره تبدیل میکنیم:
بنابراین، خواهیم داشت:
مثال هشتم ضرب کسرها
ضرب را انجام دهید.
حل: کافی است صورت را در صورت و مخرج را در مخرج ضرب کنیم.
آزمون سنجش یادگیری ضرب کسرها
در این بخش از مجله فرادرس، سطح اطلاعات شما در مبحث ضرب کسرها را با طرح سوالهای چندگزینهای میسنجیم. پس از جواب دادن به تمام سوالها، نتیجه آزمون برای شما به نمایش درمیآید.
تمرین و آزمون
حاصلضرب در چیست؟
فرمول جبری حاصلضرب دو کسر به صورت زیر نوشته میشود:
به عبارت دیگر، برای به دست آوردن حاصلضرب دو کسر، صورت آنها در هم ضرب میکنیم و درون صورت یک کسر جدید قرار میدهیم. سپس، مخرج آنها را نیز در هم ضرب میکنیم و درون مخرج کسر جدید قرار میدهیم. به این ترتیب، برای این سوال، داریم:
صورت و مخرج جواب را با استفاده از اصول سادهسازی کسر، ساده میکنیم:
کدام گزینه، جواب را نمایش میدهد؟
بر اساس فرمول ضرب کسرها، داریم:
مقادیر معلوم در سوال را درون این فرمول قرار میدهیم:
پس از سادهسازی صورت و مخرج، به جواب زیر میرسیم:
حاصلضرب چیست؟
این سوال، حاصلضرب یک عدد صحیح (3) در یک عدد کسری () را میخواهد. برای به دست آوردن این ضرب، ابتدا عدد 3 را به فرم کسری مینویسیم:
به این ترتیب، داریم:
صورت دو کسر را در یکدیگر و مخرج آنها را نیز در یکدیگر ضرب میکنیم:
با سادهسازی کسر بالا به جواب زیر میرسیم:
در ضرب اعداد صحیح در اعداد کسری، به امکان سادهسازی مخرج کسر با عدد صحیح دقت کنید. به عنوان مثال، در این سوال، عدد 3 با عدد 6 (مخرج کسر) ساده میشود و عدد 2 در مخرج کسر باقی میمانند.
جواب ، کدام گزینه است؟
برای به دست آوردن حاصلضرب یک عدد مخلوط در یک عدد کسری، ابتدا باید عدد مخلوط را به فرم کسر متعارفی بازنویسی کنیم. در این سوال، عدد ، یک عدد مخلوط است که فرم کسر متعارفی آن به صورت زیر نوشته میشود:
به این ترتیب، داریم:
حاصلضرب چیست؟
کدامیک از گزینههای زیر، جواب را نمایش میدهد؟
جمعبندی
در این آموزش از مجله فرادرس، با روش ضرب کسرها را با روشهای مختلف آشنا شدیم. همچنین، مثالهای متنوعی را برای یادگیری بهتر این روشها حل کردیم.













با سلام، احترام و سپاس بخاطر مطالب آموزنده
در کنار، ضرب عدد در کسر و برعکس، لازمه که ضرب کسر در کسر با شکل و محور هم در این مبحث مطرح بشه
با سلام؛
از بازخورد شما سپاسگزاریم. برای آشنایی بیشتر میتوانید مطلب زیر را مطالعه کنید.
ضرب کسرها — به زبان ساده + حل تمرین و مثال
با تشکر از همراهی شما با مجله فرادرس
سلام کسر۹پنجم ضرب هجده دهم چند هست ؟
خدایی اگه کسی با اینهمه مثال و آموزش بازم یاد نگیره،، بهتره بیخیال درس بشه و بره دنبال یه حرفه
سلام وقتتون بخیر
ببخشید تو مثال هفتم قسمت اول حلش وقتی کسر آمیخته رو میخواستین ناسره تبدیل کنین گویا مخرج اشتباهی ۵ نوشته شده باید ۴ باشه فکر کنم
یا اگه درسته میشه توضیح بدین؟
ممنون میشم
سلام.
بله، حق با شماست. متن بازبینی و تصحیح شد.
سپاس از همراهی و بازخوردتان.
سلام. وقتتون بخیر. من برای یادآوری نگاهی انداختم به این مطلب، بسیار خوب و روان توضیح دادید فقط مطلب یک مشکل ریز دارد که لطف بفرمایید اصلاح کنید. در “مثال پنجم ضرب کسرها” در صورت سوال خواسته شده ۲ عدد مخلوط درهم ضرب شوند اما یک عدد مخلوط به اشتباه نوشته شده و عدد ۱ در آن جا افتاده است.
ممنون از سایت عالی و محتوای با کیفیتتون و ممنون از جناب کلامی عزیز برای این سایت. خسته نباشید جناب جمیدی ممنون از شما.
سلام حسین عزیز.
اشتباه تایپی اصلاح شد.
از همراهی و بازخورد دقیق شما صمیمانه سپاسگزاریم.