در آموزشهای قبلی مجله فرادرس، درباره سری فوریه و تبدیل فوریه و سری فوریه سینوسی بحث کردیم. در این آموزش قصد داریم مفاهیم سری فوریه کسینوسی را بیان کنیم.
محتوای این مطلب جهت یادگیری بهتر و سریعتر آن، در انتهای متن به صورت ویدیویی نیز ارائه شده است.
سری فوریه برای تابعهای زوج و فرد
در مبحث مربوط به توابع متعامد ، راجع به تعامد بحث کردیم. میتوان ثابت کرد که سیستم توابع زیر در یک بازه مشخص، متعامد است:
{ 1 2 , cos ( π n x l ) , sin ( π n x l ) n = 1 , … } \Large \{\frac{1}{2},\qquad \cos (\frac{\pi nx}{l}), \qquad \sin (\frac{\pi nx}{l}) \quad n=1,\ldots\Bigr\} { 2 1 , cos ( l πn x ) , sin ( l πn x ) n = 1 , … } معادله (۱)
این سیستم روی بازه J : = [ x 0 , x 1 ] J:=[x_0,x_1] J := [ x 0 , x 1 ] x 1 − x 0 = 2 l x_1 - x_0 = 2l x 1 − x 0 = 2 l f ( x ) f(x) f ( x )
f ( x ) = 1 2 a 0 + ∑ n = 1 ∞ ( a n cos ( π n x l ) + b n sin ( π n x l ) ) \Large f(x)= \frac{1}{2}a_0 + \sum_{n=1}^\infty \bigl( a_n\cos (\frac{\pi nx}{l})+b_n \sin (\frac{\pi nx}{l}) \bigr) f ( x ) = 2 1 a 0 + n = 1 ∑ ∞ ( a n cos ( l πn x ) + b n sin ( l πn x ) ) معادله (۲)
ضرایب این سری، با توجه به مباحث سری فوریه عبارت است از:
a n = 1 l ∫ x 0 x 1 f ( x ) cos ( π n x l ) d x n = 0 , 1 , 2 , … , a_n=\Large \frac{1}{l}\int_{x_0}^{x_1} f(x)\cos (\frac{\pi nx}{l})\,dx \qquad n=0,1,2,\ldots, a n = l 1 ∫ x 0 x 1 f ( x ) cos ( l πn x ) d x n = 0 , 1 , 2 , … , معادله (۳)
و
b n = 1 l ∫ J f ( x ) sin ( π n x l ) d x n = 1 , 2 , … , b_n= \Large \frac{1}{l}\int_J f(x)\sin (\frac{\pi nx}{l})\,dx \qquad n=1,2,\ldots, b n = l 1 ∫ J f ( x ) sin ( l πn x ) d x n = 1 , 2 , … , معادله (۴)
طبق معادله پارسوال، خواهیم داشت:
l 2 ∣ a 0 ∣ 2 + ∑ n = 1 ∞ l ( ∣ a n ∣ 2 + ∣ b n ∣ 2 ) = ∫ J ∣ f ( x ) ∣ 2 d x . \Large \frac{l}{2}|a_0|^2 + \sum_{n=1}^\infty l\bigl( |a_n|^2+|b_n |^2 \bigr)=\int_J |f(x)|^2\,dx. 2 l ∣ a 0 ∣ 2 + n = 1 ∑ ∞ l ( ∣ a n ∣ 2 + ∣ b n ∣ 2 ) = ∫ J ∣ f ( x ) ∣ 2 d x . معادله (۵)
لم ۱: اگر J J J J = [ − l , l ] J=[-l,l] J = [ − l , l ]
به ازای ∀ n = 1 , 2 , … \forall n=1,2,\ldots ∀ n = 1 , 2 , … f ( x ) f(x) f ( x ) b n = 0 b_n=0 b n = 0
به ازای ∀ n = 0 , 1 , 2 , … \forall n=0,1,2,\ldots ∀ n = 0 , 1 , 2 , … f ( x ) f(x) f ( x ) a n = 0 a_n=0 a n = 0
اثبات: میدانیم که cos ( π n x l ) \cos (\frac{\pi nx}{l}) cos ( l πn x ) sin ( π n x l ) \sin (\frac{\pi nx}{l}) sin ( l πn x ) ∀ n = 1 , 2 , … \forall n=1,2,\ldots ∀ n = 1 , 2 , … b n = 0 b_n=0 b n = 0 f ( x ) f(x) f ( x )
قسمت دوم لم نیز مانند قسمت اول آن، اثبات میشود. بنابراین میتوان سری فوریه را برای توابع زوج و فرد نوشت.
خواص جبری توابع زوج و فرد
اگر f ( x ) f(x) f ( x ) − L ≤ x ≤ L -L \leq x \leq L − L ≤ x ≤ L
∫ − L L f ( x ) d x = 2 ∫ 0 L f ( x ) d x \Large \int_{-L}^L f(x) dx = 2 \int_0^L f(x) dx ∫ − L L f ( x ) d x = 2 ∫ 0 L f ( x ) d x
اگر f ( x ) f(x) f ( x ) − L ≤ x ≤ L -L \leq x \leq L − L ≤ x ≤ L
∫ − L L f ( x ) d x = 0 \Large \int_{-L}^L f(x) dx = 0 ∫ − L L f ( x ) d x = 0
سری فوریه کسینوسی
تابع f ( x ) f(x) f ( x ) [ 0 , l ] [0,l] [ 0 , l ] [ − l , l ] [-l,l] [ − l , l ] x ∈ [ − l , 0 ] x\in [-l,0] x ∈ [ − l , 0 ] f ( x ) : = f ( − x ) f(x):=f(-x) f ( x ) := f ( − x )
f ( x ) = 1 2 a 0 + ∑ n = 1 ∞ a n cos ( π n x l ) = ∑ n = 0 ∞ a n cos ( n π x L ) \Large f(x)= \frac{1}{2}a_0 + \sum_{n=1}^\infty a_n\cos (\frac{\pi nx}{l}) = \sum\limits_{n = 0}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} f ( x ) = 2 1 a 0 + n = 1 ∑ ∞ a n cos ( l πn x ) = n = 0 ∑ ∞ a n cos ( L n π x ) معادله (6)
سری فوریه معادله بالا را سری فوریه کسینوسی مینامند. سری فوریه بیان شده در معادله بالا در بازه − L ≤ x ≤ L - L \le x \le L − L ≤ x ≤ L f ( x ) f(x) f ( x ) n = 0 n = 0 n = 0
{ 1 2 , cos ( π n x l ) n = 1 , … } . \Large \{\frac{1}{2},\qquad \cos (\frac{\pi nx}{l}) \quad n=1,\ldots\}. { 2 1 , cos ( l πn x ) n = 1 , … } . معادله (۷)
ضرایب سری فوریه کسینوسی
ضرایب سری فوریه کسینوسی بر اساس معادله (۳) به دست میآید. از آنجا عبارت زیر انتگرال در معادله (۳)، یک تابع زوج است، میتوان بازه [ 0 , l ] [0,l] [ 0 , l ] [ − l , l ] [-l,l] [ − l , l ]
a n = 2 l ∫ 0 l f ( x ) cos ( π n x l ) d x n = 0 , 1 , 2 , … \Large a_n= \frac{2}{l}\int_0^l f(x)\cos (\frac{\pi nx}{l})\,dx \qquad n=0,1,2,\ldots a n = l 2 ∫ 0 l f ( x ) cos ( l πn x ) d x n = 0 , 1 , 2 , … معادله (۸)
به این ترتیب، معادله (۵) به صورت زیر در خواهد آمد:
l 4 ∣ a 0 ∣ 2 + ∑ n = 1 ∞ l 2 ∣ a n ∣ 2 = ∫ 0 l ∣ f ( x ) ∣ 2 d x . \Large \frac{l}{4}|a_0|^2 +\sum_{n=1}^\infty \frac{l}{2} |a_n|^2= \int_0^l |f(x)|^2\,dx. 4 l ∣ a 0 ∣ 2 + n = 1 ∑ ∞ 2 l ∣ a n ∣ 2 = ∫ 0 l ∣ f ( x ) ∣ 2 d x . معادله (9)
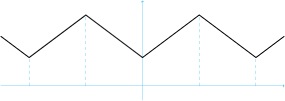
این سری فوریه، با دوره تناوب 2 l 2l 2 l
شکل زیر، یک مثال از تبدیل فوریه کسینوسی را نشان میدهد:
محاسبه ضرایب سری فوریه کسینوسی
ضرایب سری فوریه کسینوسی از تعامد تابع کسینوس به دست آمدهاند. طبق قضیه تعامد داریم:
$$\int_{{ - L}}^{L}{{\cos \left( {\frac{{n\pi x}}{L}} \right)\cos \left( {\frac{{m\pi x}}{L}} \right)\,dx}} = \left\{ {\begin{array}{*{20}{l}}{2L}&{{\mbox{if }}n = m = 0}\\L&{{\mbox{if }}n = m \ne 0}\\0&{{\mbox{if }}n \ne m}\end{array}} \right.$$
اگر دو طرف معادله (۶) را در عبارت cos ( m π x L ) \cos \left( {\frac{{m\pi x}}{L}} \right) cos ( L mπ x )
f ( x ) cos ( m π x L ) = ∑ n = 0 ∞ a n cos ( n π x L ) cos ( m π x L ) \Large f\left( x \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right) = \sum\limits_{n = 0}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right)} f ( x ) cos ( L m π x ) = n = 0 ∑ ∞ a n cos ( L n π x ) cos ( L m π x )
با انتگرالگیری از دو طرف معادله بالا در بازه x = − L x = - L x = − L x = L x = L x = L
∫ − L L f ( x ) cos ( m π x L ) d x = ∫ − L L ∑ n = 0 ∞ a n cos ( n π x L ) cos ( m π x L ) d x = ∑ n = 0 ∞ a n ∫ − L L cos ( n π x L ) cos ( m π x L ) d x \Large \begin{align*}\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}} & = \int_{{\, - L}}^{L}{{\sum\limits_{n = 0}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right)} }}\,dx\\ & = \sum\limits_{n = 0}^\infty {{a_n}\int_{{\, - L}}^{{\,L}}{{\cos \left( {\frac{{n\,\pi x}}{L}} \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}}} \end{align*} ∫ − L L f ( x ) cos ( L m π x ) d x = ∫ − L L n = 0 ∑ ∞ a n cos ( L n π x ) cos ( L m π x ) d x = n = 0 ∑ ∞ a n ∫ − L L cos ( L n π x ) cos ( L m π x ) d x
توجه کنید که در معادله بالا، جای سری و انتگرال عوض شده است. میدانیم که انتگرال سمت راست معادله بالا برابر صفر خواهد بود مگر آنکه n = m n = m n = m − L ≤ x ≤ L - L \le x \le L − L ≤ x ≤ L m m m n n n
اگر m = 0 m = 0 m = 0
∫ − L L f ( x ) d x = a 0 ( 2 L ) ⇒ a 0 = 1 2 L ∫ − L L f ( x ) d x \int_{{\, - L}}^{{\,L}}{{f\left( x \right)dx}} = {a_{\,0}}\left( {2L} \right)\,\,\,\,\,\,\,\, \Rightarrow\,\,\,\,\,\,\,\,{a_{\,0}} = \frac{1}{{2L}}\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\,dx}} ∫ − L L f ( x ) d x = a 0 ( 2 L ) ⇒ a 0 = 2 L 1 ∫ − L L f ( x ) d x
اگر m ≠ 0 m \ne 0 m = 0
∫ − L L f ( x ) cos ( m π x L ) d x = a m ( L ) ⇒ a m = 1 L ∫ − L L f ( x ) cos ( m π x L ) d x \int_{{\, - L}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}} = {a_{\,m}}\left( L \right)\,\,\,\,\,\,\,\, \Rightarrow \,\,\,\,\,\,\,\,{a_{\,m}} = \frac{1}{L}\int_{{\, - L}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{m\,\pi x}}{L}} \right)\,dx}} ∫ − L L f ( x ) cos ( L m π x ) d x = a m ( L ) ⇒ a m = L 1 ∫ − L L f ( x ) cos ( L m π x ) d x
به طور خلاصه، سری فوریه کسینوسی برای تابع زوج f ( x ) f(x) f ( x ) − L ≤ x ≤ L - L \le x \le L − L ≤ x ≤ L
$$ f\left( x \right)=\sum\limits_{n=0}^{\infty }{{{a}_{n}}\cos \left( \frac{n\,\pi x}{L} \right)} \hspace{0.25in}, \,\,\, {{a}_{n}}=\left\{ \begin{array}{*{35}{l}} \displaystyle<br />
\frac{1}{2L}\int_{\,-L}^{\,L}{f\left( x \right)\,dx} & \,\,\,\,\,n=0 \\ \displaystyle<br />
\frac{1}{L}\int_{\,-L}^{\,L}{f\left( x \right)\cos \left( \frac{n\,\pi x}{L} \right)\,dx} & \,\,\,\,\,n\ne 0 \\<br />
\end{array} \right.$$
همانطور که مشخص است، f ( x ) f(x) f ( x )
$$\Large {a_n} = \left\{ {\begin{array}{*{20}{l}}{\displaystyle \frac{1}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\,dx}}}&{\,\,\,\,\,n = 0}\\{\displaystyle \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}}&{\,\,\,\,\,n \ne 0}\end{array}} \right.$$
با بیان یک مثال، مفهوم سری فوریه کسینوسی واضحتر خواهد شد.
مثال ۱
سری فوریه کسینوسی تابع f ( x ) = x 2 f(x) = x^2 f ( x ) = x 2 − L ≤ x ≤ L -L \leq x \leq L − L ≤ x ≤ L
حل: واضح است که تابع f ( x ) f(x) f ( x )
a 0 = 1 L ∫ 0 L f ( x ) d x = 1 L ∫ 0 L x 2 d x = 1 L ( L 3 3 ) = L 2 3 \Large {a_0} = \frac{1}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\,dx}} = \frac{1}{L}\int_{{\,0}}^{{\,L}}{{{x^2}\,dx}} = \frac{1}{L}\left( {\frac{{{L^3}}}{3}} \right) = \frac{{{L^2}}}{3} a 0 = L 1 ∫ 0 L f ( x ) d x = L 1 ∫ 0 L x 2 d x = L 1 3 L 3 = 3 L 2
همانطور که میدانیم، a 0 a_0 a 0 a n a_n a n
a n = 2 L ∫ 0 L f ( x ) cos ( n π x L ) d x = 2 L ∫ 0 L x 2 cos ( n π x L ) d x = 2 L ( L n 3 π 3 ) ( 2 L n π x cos ( n π x L ) + ( n 2 π 2 x 2 − 2 L 2 ) sin ( n π x L ) ) ∣ 0 L = 2 n 3 π 3 ( 2 L 2 n π cos ( n π ) + ( n 2 π 2 L 2 − 2 L 2 ) sin ( n π ) ) = 4 L 2 ( − 1 ) n n 2 π 2 n = 1 , 2 , 3 , … \Large \begin{align*}{a_n} & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{{x^2}\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\\ & = \frac{2}{L}\left. {\left( {\frac{L}{{{n^3}{\pi ^3}}}} \right)\left( {2Ln\pi x\cos \left( {\frac{{n\,\pi x}}{L}} \right) + \left( {{n^2}{\pi ^2}{x^2} - 2{L^2}} \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right)} \right)} \right|_0^L\\ & = \frac{2}{{{n^3}{\pi ^3}}}\left( {2{L^2}n\pi \cos \left( {n\,\pi } \right) + \left( {{n^2}{\pi ^2}{L^2} - 2{L^2}} \right)\sin \left( {n\,\pi } \right)} \right)\\ & = \frac{{4{L^2}{{\left( { - 1} \right)}^n}}}{{{n^2}{\pi ^2}}}\hspace{0.25in}\hspace{0.25in}n = 1,2,3, \ldots \end{align*} a n = L 2 ∫ 0 L f ( x ) cos ( L n π x ) d x = L 2 ∫ 0 L x 2 cos ( L n π x ) d x = L 2 ( n 3 π 3 L ) ( 2 L nπ x cos ( L n π x ) + ( n 2 π 2 x 2 − 2 L 2 ) sin ( L n π x ) ) 0 L = n 3 π 3 2 ( 2 L 2 nπ cos ( n π ) + ( n 2 π 2 L 2 − 2 L 2 ) sin ( n π ) ) = n 2 π 2 4 L 2 ( − 1 ) n n = 1 , 2 , 3 , …
پس ضرایب سری فوریه کسینوسی برای این تابع به صورت زیر است:
a 0 = L 2 3 , a n = 4 L 2 ( − 1 ) n n 2 π 2 , n = 1 , 2 , 3 , … {a_0} = \frac{{{L^2}}}{3}\hspace{0.25in},{a_n} = \frac{{4{L^2}{{\left( { - 1} \right)}^n}}}{{{n^2}{\pi ^2}}},\,\,\,\,n = 1,2,3, \ldots a 0 = 3 L 2 , a n = n 2 π 2 4 L 2 ( − 1 ) n , n = 1 , 2 , 3 , …
بنابراین سری فوریه تابع f ( x ) f(x) f ( x )
x 2 = ∑ n = 0 ∞ a n cos ( n π x L ) = a 0 + ∑ n = 1 ∞ a n cos ( n π x L ) = L 2 3 + ∑ n = 1 ∞ 4 L 2 ( − 1 ) n n 2 π 2 cos ( n π x L ) {x^2} = \sum\limits_{n = 0}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} = {a_0} + \sum\limits_{n = 1}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} = \frac{{{L^2}}}{3} + \sum\limits_{n = 1}^\infty {\frac{{4{L^2}{{\left( { - 1} \right)}^n}}}{{{n^2}{\pi ^2}}}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} x 2 = n = 0 ∑ ∞ a n cos ( L n π x ) = a 0 + n = 1 ∑ ∞ a n cos ( L n π x ) = 3 L 2 + n = 1 ∑ ∞ n 2 π 2 4 L 2 ( − 1 ) n cos ( L n π x )
بسط نیمدامنه سری فوریه کسینوسی
حال فرض کنید بخواهیم سری فوریه کسینوسی یک تابع غیر زوج را بیابیم. همانطور که میدانیم، سری فوریه فقط برای توابع متناوب تعریف میشود، بنابراین باید تابع را گسترش دهیم تا به یک تابع زوج و متناوب تبدیل شود. تابع f ( x ) f(x) f ( x ) 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L − L ≤ x ≤ L - L \le x \le L − L ≤ x ≤ L f ( x ) f(x) f ( x ) − L ≤ x ≤ L - L \le x \le L − L ≤ x ≤ L
$$ g\left( x \right) =\Bigg\{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{f\left( { - x} \right)}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}}.$$
تابع g ( x ) g(x) g ( x )
g ( − x ) = f ( − ( − x ) ) = f ( x ) = g ( x ) for g\left( -x \right)=f\left( -\left( -x \right) \right)=f\left( x \right)=g\left( x \right) \hspace{0.25in} \text{for} g ( − x ) = f ( − ( − x ) ) = f ( x ) = g ( x ) for 0 0 0
مشاهده میشود که روی بازه 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L g ( x ) g(x) g ( x ) f ( x ) f(x) f ( x ) f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) f ( x ) f(x) f ( x ) − L ≤ x ≤ L -L \le x \le L − L ≤ x ≤ L
حال میخواهیم دریابیم چگونه میتوان بر اساس گسترش زوج یک تابع، بسط فوریه هر تابعی را در بازه 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L
اگر تابع f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) g ( x ) g(x) g ( x ) − L ≤ x ≤ L -L \le x \le L − L ≤ x ≤ L
$$g\left( x \right) = \sum\limits_{n = 0}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \hspace{0.25in}{a_n} = \left\{ {\begin{array}{*{20}{l}}{\displaystyle \frac{1}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\,dx}}}&{\,\,\,\,\,n = 0}\\{\displaystyle \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}}&{\,\,\,\,\,n \ne 0}\end{array}} \right.$$
در بازه 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L f ( x ) f(x) f ( x ) g ( x ) g(x) g ( x ) f ( x ) f\left( x \right) f ( x ) 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L
$$f\left( x \right) = \sum\limits_{n = 0}^\infty {{a_n}\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \hspace{0.25in}{a_n} = \left\{ {\begin{array}{*{20}{l}}{\displaystyle \frac{1}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\,dx}}}&{\,\,\,\,\,n = 0}\\{\displaystyle \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}}&{\,\,\,\,\,n \ne 0}\end{array}} \right.$$
در ادامه به بیان چند مثال برای یافتن سری فوریه کسینوسی توابع غیر زوج، خواهیم پرداخت:
مثال ۲
سری فوریه کسینوسی تابع f ( x ) = L − x f\left( x \right) = L - x f ( x ) = L − x 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L
حل: ابتدا باید تابع f ( x ) f(x) f ( x )
گسترش زوج تابع f ( x ) f(x) f ( x )
$$\begin{align*}g\left( x \right) & = \Bigg\{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{f\left( { - x} \right)}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\\ & = \Bigg\{ {\begin{array}{*{20}{l}}{L - x}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{L + x}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\end{align*}$$
در شکل زیر، تابع و گسترش زوج آن نشان داده شده است:
ضرایب سری فوریه کسینوسی به صورت زیر هستند:
a 0 = 1 L ∫ 0 L f ( x ) d x = 1 L ∫ 0 L L − x d x = L 2 {a_0} = \frac{1}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\,dx}} = \frac{1}{L}\int_{{\,0}}^{{\,L}}{{L - x\,dx}} = \frac{L}{2} a 0 = L 1 ∫ 0 L f ( x ) d x = L 1 ∫ 0 L L − x d x = 2 L
a n = 2 L ∫ 0 L f ( x ) cos ( n π x L ) d x = 2 L ∫ 0 L ( L − x ) cos ( n π x L ) d x = 2 L ( L n 2 π 2 ) ( n π ( L − x ) sin ( n π x L ) − L cos ( n π x L ) ) ∣ 0 L = 2 L ( L n 2 π 2 ) ( − L cos ( n π ) + L ) = 2 L n 2 π 2 ( 1 + ( − 1 ) n + 1 ) n = 1 , 2 , 3 , … \begin{align*}{a_n} & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{\left( {L - x} \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\\ & = \frac{2}{L}\left. {\left( {\frac{L}{{{n^2}{\pi ^2}}}} \right)\left( {n\pi \left( {L - x} \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right) - L\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \right)} \right|_0^L\\ & = \frac{2}{L}\left( {\frac{L}{{{n^2}{\pi ^2}}}} \right)\left( { - L\cos \left( {n\,\pi } \right) + L} \right) = \frac{{2L}}{{{n^2}{\pi ^2}}}\left( {1 + {{\left( { - 1} \right)}^{n + 1}}} \right)\hspace{0.25in}\hspace{0.25in}n = 1,2,3, \ldots \end{align*} a n = L 2 ∫ 0 L f ( x ) cos ( L n π x ) d x = L 2 ∫ 0 L ( L − x ) cos ( L n π x ) d x = L 2 ( n 2 π 2 L ) ( nπ ( L − x ) sin ( L n π x ) − L cos ( L n π x ) ) 0 L = L 2 ( n 2 π 2 L ) ( − L cos ( n π ) + L ) = n 2 π 2 2 L ( 1 + ( − 1 ) n + 1 ) n = 1 , 2 , 3 , …
بنابراین سری فوریه تابع f ( x ) f(x) f ( x )
f ( x ) = L 2 + ∑ n = 1 ∞ 2 L n 2 π 2 ( 1 + ( − 1 ) n + 1 ) cos ( n π x L ) f\left( x \right) = \frac{L}{2} + \sum\limits_{n = 1}^\infty {\frac{{2L}}{{{n^2}{\pi ^2}}}\left( {1 + {{\left( { - 1} \right)}^{n + 1}}} \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)} f ( x ) = 2 L + n = 1 ∑ ∞ n 2 π 2 2 L ( 1 + ( − 1 ) n + 1 ) cos ( L n π x )
مثال ۳
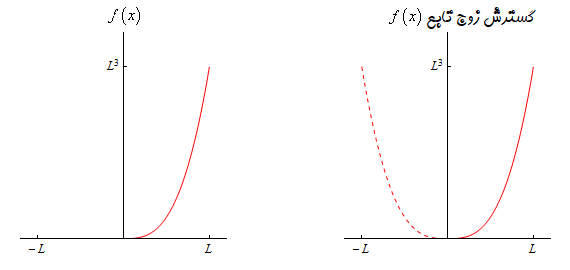
سری فوریه کسینوسی تابع f ( x ) = x 3 f\left( x \right) = {x^3} f ( x ) = x 3 0 ≤ x ≤ L 0 \le x \le L 0 ≤ x ≤ L
حل: گسترش زوج این تابع به صورت زیر است:
$$\begin{align*}g\left( x \right) & = \Bigg \{ {\begin{array}{*{20}{l}}{f\left( x \right)}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{f\left( { - x} \right)}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\\ & = \Bigg \{ {\begin{array}{*{20}{l}}{{x^3}}&{\,\,\,\,{\mbox{if }}0 \le x \le L}\\{ - {x^3}}&{\,\,\,\,{\mbox{if }} - L \le x \le 0}\end{array}} .\end{align*}$$
در شکل زیر، تابع مسئله و گسترش آن نشان داده شده است:
a 0 = 1 L ∫ 0 L f ( x ) d x = 1 L ∫ 0 L x 3 d x = L 3 4 {a_0} = \frac{1}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\,dx}} = \frac{1}{L}\int_{{\,0}}^{{\,L}}{{{x^3}\,dx}} = \frac{{{L^3}}}{4} a 0 = L 1 ∫ 0 L f ( x ) d x = L 1 ∫ 0 L x 3 d x = 4 L 3
a n = 2 L ∫ 0 L f ( x ) cos ( n π x L ) d x = 2 L ∫ 0 L x 3 cos ( n π x L ) d x = 2 L ( L n 4 π 4 ) ( n π x ( n 2 π 2 x 2 − 6 L 2 ) sin ( n π x L ) + ( 3 L n 2 π 2 x 2 − 6 L 3 ) cos ( n π x L ) ) ∣ 0 L = 2 L ( L n 4 π 4 ) ( n π L ( n 2 π 2 L 2 − 6 L 2 ) sin ( n π ) + ( 3 L 3 n 2 π 2 − 6 L 3 ) cos ( n π ) + 6 L 3 ) = 2 L ( 3 L 4 n 4 π 4 ) ( 2 + ( n 2 π 2 − 2 ) ( − 1 ) n ) = 6 L 3 n 4 π 4 ( 2 + ( n 2 π 2 − 2 ) ( − 1 ) n ) n = 1 , 2 , 3 , … \begin{align*}{a_n} & = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{f\left( x \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}} = \frac{2}{L}\int_{{\,0}}^{{\,L}}{{{x^3}\cos \left( {\frac{{n\,\pi x}}{L}} \right)\,dx}}\\ & = \frac{2}{L}\left. {\left( {\frac{L}{{{n^4}{\pi ^4}}}} \right)\left( {n\pi x\left( {{n^2}{\pi ^2}{x^2} - 6{L^2}} \right)\sin \left( {\frac{{n\,\pi x}}{L}} \right) + \left( {3L{n^2}{\pi ^2}{x^2} - 6{L^3}} \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)} \right)} \right|_0^L\\ & = \frac{2}{L}\left( {\frac{L}{{{n^4}{\pi ^4}}}} \right)\left( {n\pi L\left( {{n^2}{\pi ^2}{L^2} - 6{L^2}} \right)\sin \left( {n\,\pi } \right) + \left( {3{L^3}{n^2}{\pi ^2} - 6{L^3}} \right)\cos \left( {n\,\pi } \right) + 6{L^3}} \right)\\ & = \frac{2}{L}\left( {\frac{{3{L^4}}}{{{n^4}{\pi ^4}}}} \right)\left( {2 + \left( {{n^2}{\pi ^2} - 2} \right){{\left( { - 1} \right)}^n}} \right) = \frac{{6{L^3}}}{{{n^4}{\pi ^4}}}\left( {2 + \left( {{n^2}{\pi ^2} - 2} \right){{\left( { - 1} \right)}^n}} \right)\hspace{0.25in}\,\,\,\,\,\,\,\,n = 1,2,3, \ldots \end{align*} a n = L 2 ∫ 0 L f ( x ) cos ( L n π x ) d x = L 2 ∫ 0 L x 3 cos ( L n π x ) d x = L 2 ( n 4 π 4 L ) ( nπ x ( n 2 π 2 x 2 − 6 L 2 ) sin ( L n π x ) + ( 3 L n 2 π 2 x 2 − 6 L 3 ) cos ( L n π x ) ) 0 L = L 2 ( n 4 π 4 L ) ( nπ L ( n 2 π 2 L 2 − 6 L 2 ) sin ( n π ) + ( 3 L 3 n 2 π 2 − 6 L 3 ) cos ( n π ) + 6 L 3 ) = L 2 ( n 4 π 4 3 L 4 ) ( 2 + ( n 2 π 2 − 2 ) ( − 1 ) n ) = n 4 π 4 6 L 3 ( 2 + ( n 2 π 2 − 2 ) ( − 1 ) n ) n = 1 , 2 , 3 , …
بنابراین سری فوریه کسینوسی تابع f ( x ) f(x) f ( x )
f ( x ) = L 3 4 + ∑ n = 1 ∞ 6 L 3 n 4 π 4 ( 2 + ( n 2 π 2 − 2 ) ( − 1 ) n ) cos ( n π x L ) f\left( x \right) = \frac{{{L^3}}}{4} + \sum\limits_{n = 1}^\infty {\frac{{6{L^3}}}{{{n^4}{\pi ^4}}}\left( {2 + \left( {{n^2}{\pi ^2} - 2} \right){{\left( { - 1} \right)}^n}} \right)\cos \left( {\frac{{n\,\pi x}}{L}} \right)} f ( x ) = 4 L 3 + n = 1 ∑ ∞ n 4 π 4 6 L 3 ( 2 + ( n 2 π 2 − 2 ) ( − 1 ) n ) cos ( L n π x )
در آموزش بعدی از این سری آموزشها در مجله فرادرس، به بررسی سری فوریه مختلط خواهیم پرداخت.
در صورتی که به مباحث مرتبط در زمینه ریاضیات پایه علاقهمند هستید، آموزشهای زیر به شما پیشنهاد میشوند:
^^
فیلم های آموزش سری فوریه کسینوسی – به زبان ساده (+ دانلود فیلم آموزش رایگان) فیلم آموزشی سری فوریه کسینوسی فیلم آموزشی حل مثال از سری فوریه کسینوسی 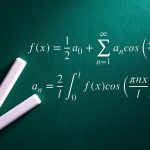
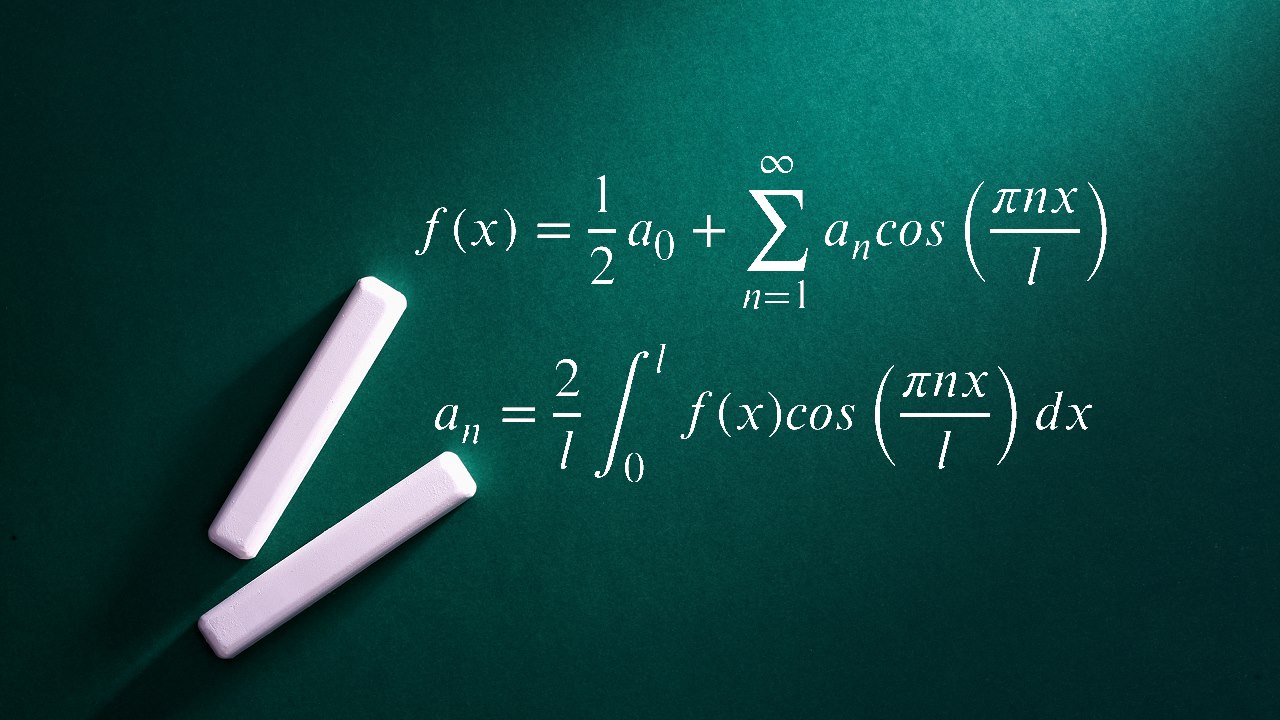
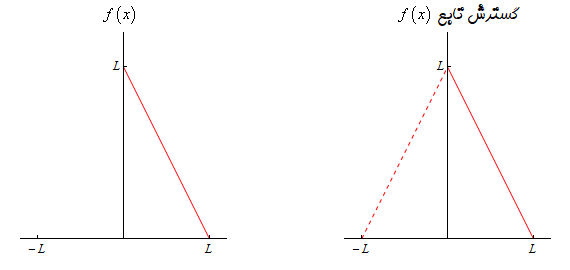












خیلی خوب بود
حاجی دمت گرم…عالی بود..ممنونم
بسیار عالی بود