زیرمشتق و خواص آن — به زبان ساده

یکی از مفاهیم و اصطلاحات رایج در ریاضیات، مشتق (Derivation) و مشتق‌پذیری (Derivative) است. شرایط خاصی برای توابع در نظر گرفته می‌شود تا مشتق‌پذیر باشند. معمول‌ترین آن‌ها با توجه به تعریف حد (Limit) و همچنین تعریف مشتق براساس حد صورت می‌گیرد. براین اساس هر تابعی که مشتق‌پذیر باشد، پیوسته بوده ولی عکس آن صحیح نیست. به این معنی که ممکن است تابعی (مانند تابع قدرمطلق) پیوسته بوده ولی در یک یا بعضی از نقاطش، مشتق‌پذیر نباشد. چنین وضعیتی دانشمندان را به سوی تعریف دیگری سوق داد که بتوانند در چنین مواردی مفهومی مانند زیرمشتق را ارائه دهند. این کار بخصوص برای توابع محدب کارساز است زیرا رفتار زیرمشتق شبیه مشتق بوده و بخصوص برای بهینه سازی توابعی محدب مناسب است.

در این نوشتار براساس شرایط ساده‌تر و برای «توابع محدب» (Convex Function)، مفهوم جدیدی از مشتق ارائه می‌شود که به آن «زیرمشتق» (Subderviation) می‌گویند. تابعی را که برای همه اعضای دامنه‌اش زیرمشتق داشته باشد، «زیرمشتق‌پذیر» (Subderviative) می‌نامند.

برای آشنایی بیشتر با مفهوم حد و مشتق بهتر است مطالب دیگر مجله فرادرس با عنوان‌های حد در ریاضی — به زبان ساده و مشتق — به زبان ساده را مطالعه کنید. همچنین خواندن پیوستگی (Continuity) و تابع پیوسته (Continues Function) — به زبان ساده و توابع محدب و مقعر — از صفر تا صد نیز خالی از لطف نیست.

زیرمشتق و خواص آن

در ریاضیات سه مفهوم «زیرمشتق‌» (Subderviative)، «زیرگرادیان» (Sub-gradient) و «زیردیفرانسیل» (Sub-differential) به یک موضوع اشاره دارند و تعمیمی برای مفاهیم اولیه مشتق، گردیان و دیفرانسیل هستند. در حقیقت این سه اصطلاح، مشتق‌پذیری برای توابع محدب بدون شرط وجود دیفرانسیل را برآورده می‌کنند.

فیلم آموزش ریاضی عمومی 2 – جامع و کاربردی در فرادرس

کلیک کنید

زیردیفرانسیل برای یک تابع محدب اولین بار توسط «ژان ماریو» (Jean Moreau) ریاضی‌دان فرانسوی و «رالف راکفلر» (Ralph Tyrrell Rockafellar) ریاضی‌دان آمریکایی در اوایل سال 1960 معرفی شد. همچنین در دهه ۸۰ میلادی نیز «زیردیفرانسیل تعمیم یافته» (Generalize Sub-differential) برای توابع «غیرمحدب» (Non-Convex) توسط «کلارک» (Clarke) و «راکفلر» (Rockafellar) طی مقاله‌ای، مطرح و به کار گرفته شد.

در اکثر مواقع از زیرمشتق و زیردیفرانسیل برای توابع محدب و مباحث مربوط به بهینه‌سازی چنین توابع در «تحلیل مسائل محدب» (Convex Analysis) استفاده می‌کنند. پس بهتر است ابتدا به مفهوم و معنی تابع محدب بپردازیم.

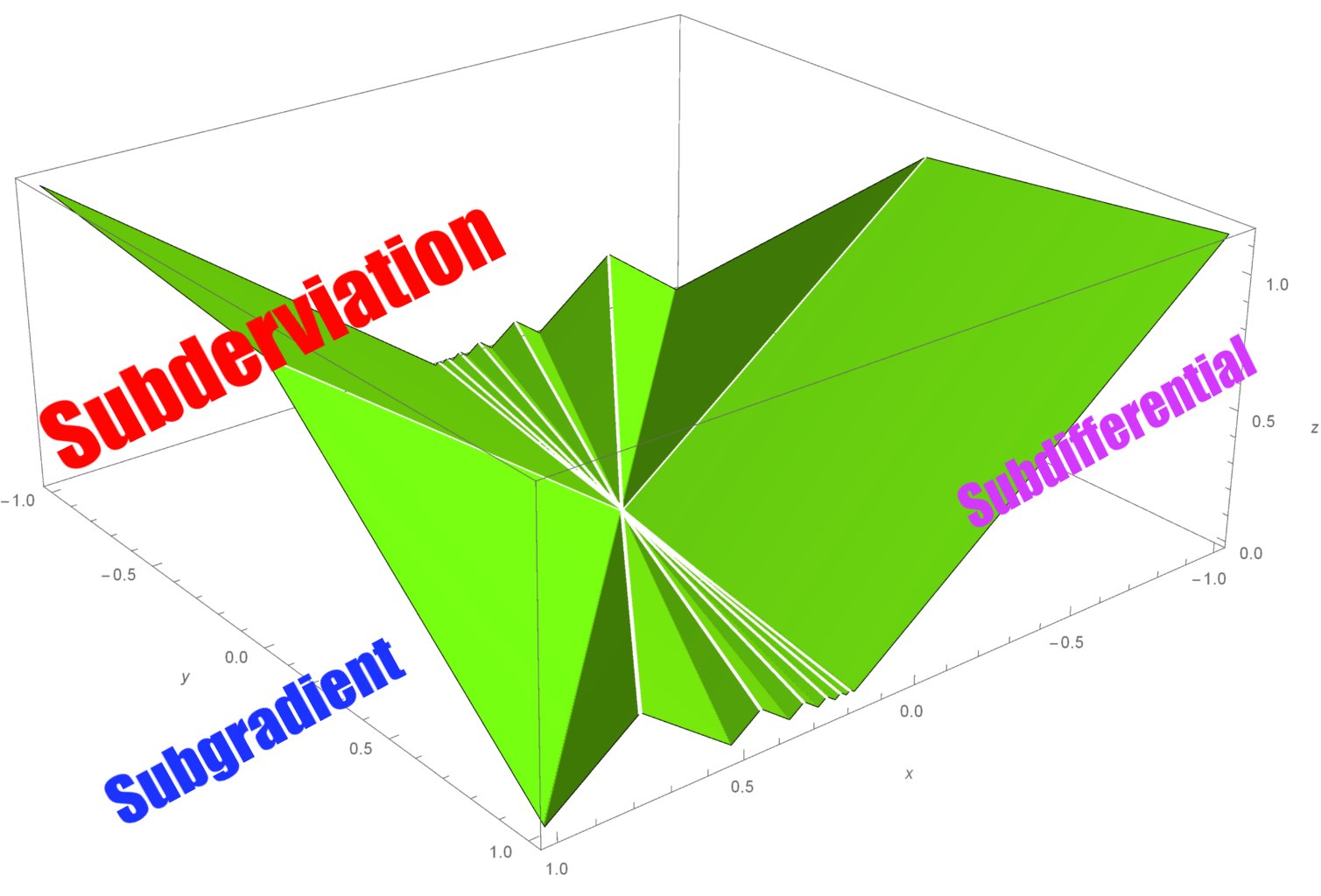
تابع $$f$$ را روی دامنه‌اش محدب (Convex) گویند اگر برای هر بازه از دامنه آن مثل $$[x_1,x_2]$$، مقدار تابع برای این فاصله از مقدار خطی که این دو نقطه را به یکدیگر متصل می‌کند کوچکتر یا مساوی باشد. برای روشن شدن موضوع به تصویر زیر توجه کنید.

دو مقدار $$x_1$$ و $$x_2$$ را با شرط $$x_1 < x_2$$ در نظر بگیرید. مقدار تابع $$f(x)$$ در تمامی مقادیری از محور افقی که در بین $$x_1$$ و $$x_2$$ قرار گرفته‌اند، از مقدار عرض خطی که دو نقطه $$(x_1 , f(x_1))$$ و $$(x_2,f(x_2))$$ را به یکدیگر وصل کرده، کوچکتر است. واضح است که براساس $$t>0$$ می‌توان تمامی نقاط در این فاصله را ایجاد کرد. این کار در رابطه ۱ صورت گرفته است.

طبق تعریف، تابع $$f$$ را روی دامنه‌اش ($$D_f$$) محدب گویند، اگر:

$$\large{ \displaystyle \forall x_{1},x_{2}\in D_f \;,\forall t \in [0,1] : \qquad f(tx_{1} + ( 1 - t) x_{2})\leq tf(x_{1})  +( 1 - t)f(x_{2})}$$

رابطه ۱‌: تعریف تابع محدب

فیلم آموزش حل معادلات دیفرانسیل با متمتیکا Mathematica در فرادرس

کلیک کنید

توابعی مانند $$f(x)=x^2$$ و $$f(x)=|x|^p, \;\;p \geq 1$$ محدب هستند. همچنین تابع $$e^x$$ نیز محدب محسوب می‌شود.

برای مثال تابع $$f(x)=x^2$$ را مورد بررسی قرار می‌دهیم. دو نقطه $$x_1=0$$ و $$x_2=1$$ و مقدار تابع در این دو نقطه را در نظر بگیرید.

$$\large  f(x_1) = f( 0 ) = 0^2 = 0  , \;\;\; f( x_2 ) = f(1) = 1^2 = 1$$

معادله خطی که این دو نقطه $$(0,0) , (1,1)$$ را به یکدیگر متصل می‌کند به صورت زیر است:

$$\large  y - 0 = \dfrac{1 - 0}{ 1 - 0} (x - 0) \rightarrow y = x$$

می‌دانیم که برای مقادیر مثبت کوچکتر از ۱، مربع این مقادیر از خودشان کوچکتر است. در نتیجه همیشه مقدار تابع $$f(x)=x^2$$ در این بازه از مقدار خطی که دو نقطه $$(0,0)$$ و $$(1,1)$$ را به یکدیگر وصل می‌کند کوچکتر است.

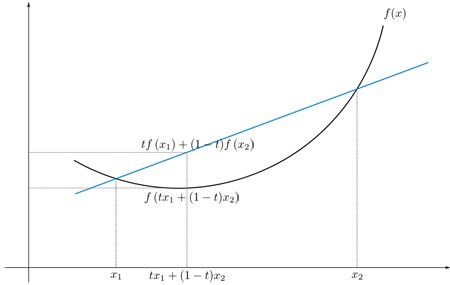
در ادامه با تابع قدر مطلق به عنوان یک تابع محدب بیشتر کار خواهیم کرد. در تصویر ۲، نمودار تابع قدر مطلق $$f(x) = |x|$$‌ را مشاهده می‌کنید که در شرایط مربوط به تابع محدب صدق می‌کند. تعریف ریاضی تابع محدب نیز براساس مقادیر میانگین وزنی برحسب $$t$$ در رابطه ۱ دیده می‌شود.

فرض کنید تابع حقیقی مقدار $$f$$ وجود داشته باشد که محدب است. ممکن است چنین تابعی در همه دامنه‌اش، مشتق‌پذیر نباشد. برای مثال تابع زیر از این گونه توابع محسوب می‌شود.

$$\large  | x | , \; \; x \in R$$

بر اساس تصویر زیر که مربوط به تابع قدرمطلق در رابطه بالا است، محدب بودن به خوبی دیده می‌شود. از طرفی واضح است که این تابع در صفر مشتق‌پذیر نیست.

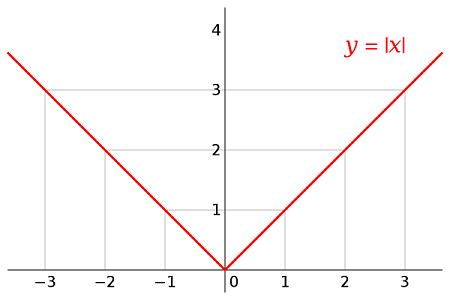
هر چند این تابع پیوسته است ولی در نقطه $$x = 0$$ به علت وجود تغییر جهت و نوک در نقطه صفر، تابع مشتق‌پذیر نیست. زیرا طبق مفهوم مشتق باید داشته باشیم:

$$\large \lim_{x \to 0} \dfrac{|x|}{x} = \begin{cases} 1 & x \geq 0\\ -1 & x < 0 \end{cases}$$

رابطه ۲

پس چنین تابعی مشتق‌پذیر در $$x = 0$$‌ نیست در نتیجه نمی‌توان آ‌ن را در کل دامنه‌اش، مشتق‌پذیر خواند.

ولی توجه داشته باشید که تابع $$f(x) = |x|$$، طبق رابطه ۱، محدب است زیرا در این صورت برای تابع قدر مطلق، داریم:

$$\large { \displaystyle \forall x_{1}, x_{2} \in D_f \; ;\; \forall t\in [0,1] : \quad |tx_{1} + (1 - t) x_{2}|\leq t|x_{1}| + (1-t)|x_{2}|}$$

مشخص است که رابطه بالا به لحاظ خصوصیات تابع قدرمطلق و نامساوی‌های مربوطه به راحتی تعیین می‌شود. در نتیجه تابع قدرمطلق، محدب بوده ولی مشتق‌پذیر نیست.

زیرمشتق و تعریف آن

به منظور رفع مشکل مشتق‌پذیری توابع در نقاط نوک تیز (بخصوص برای توابع محدب)، مفهوم جدیدی به نام زیرمشتق ارائه شده است. در ادامه تعریف زیر مشتق را خواهیم دید.

فیلم آموزش مشتق گیری و انتگرال گیری عددی در محاسبات عددی (رایگان) در فرادرس

کلیک کنید

تعریف زیر مشتق: زیرمشتق‌ تابع محدب مانند $$f$$ که دارای مقادیری از اعداد حقیقی است در نقطه $$x_0$$ از دامنه آن برابر است با $$c$$‌ اگر رابطه زیر برقرار باشد.

$$\large f(x) - f(x_{0}) \geq c (x - x_{0}) ,\;\;\; \forall x \in D_f$$

رابطه ۳

به این ترتیب اگر تابعی، در این تعریف برای همه مقادیر دامنه‌اش، دارای زیرمشتق باشد، آن را زیرمشتق‌پذیر می‌نامند. واضح است که مقدار $$c$$ منحصر به فرد نیست. در نتیجه ممکن است زیر مشتق یک تابع به صورت یک مجموعه از مقادیر محسوب شود که در رابطه ۳، صدق کنند.

نکته: ممکن است در یک بازه $$[a,b]$$ شرایط زیرمشتق‌پذیری تابع $$f$$ برقرار باشد. در این صورت براساس حد‌های یک طرفه خواهیم داشت:

$$\large { \displaystyle a = \lim _{{x \to x_{0}^{-}}}{\frac {f(x) - f (x_{0})}{x - x_{0}}}} \\ \large { \displaystyle b = \lim _{x \to x_{0}^{+}}{\frac {f (x) - f (x_{0})}{x - x_{0}}}}$$

مجموعه $$[a,b]$$ را که شامل همه نقاط زیر‌مشتق تابع $$f$$ در نقطه $$x_0$$ است، زیردیفرانسیل آن تابع می‌نامند. از آنجایی که تابع $$f$$، محدب است، اگر زیردیفرانسیل آن در نقطه $$x_0$$ شامل دقیقا یک نقطه باشد، آنگاه تابع $$f$$ را مشتق‌پذیر در $$x_0$$ می‌گویند.

مثال

تابع $$f(x)=|x|$$ را در نظر بگیرید. در قسمت قبل نشان دادیم که این تابع، محدب است. در این صورت زیردیفرانسیل (مجموعه نقاط زیرمشتق‌ آن) در فاصله بسته $$[-1,1]$$ قرار دارد. واضح است که زیردیفرانسیل برای نقطه‌های کوچکتر از ۰ برابر است با $$-1$$

$$\large -1=\lim _{{x\to 0^{-}}}{\frac {|x - 0|}{x - 0}},\;\;x<0$$

و برای مجموعه نقاط $$x>0$$ داریم:

$$\large 1=\lim _{{x\to 0^{+}}}{\frac {|x - 0|}{x - 0}},\;\;x>0$$

مقادیر حاصل از زیرمشتق تابع قدرمطلق، درست مانند تابع علامت ظاهر می‌شوند. ولی زیرمشتق در نقطه ۰، یک مقدار ثابت نشده است و شامل همه مقادیر زیرمشتق‌های ممکن خواهد بود.

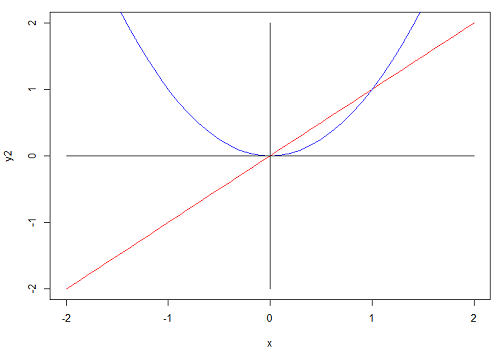
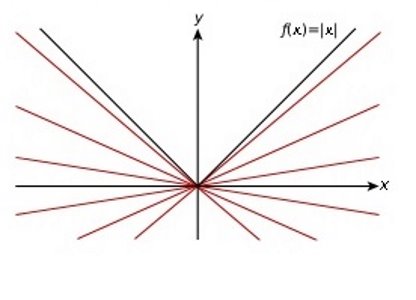
در تصویر زیر مجموعه دیفرانسیل تابع $$f(x) = | x |$$ براساس خطوط مختلف نشان داده شده است. همانطور که دیده می‌شود، مجموعه نقاطی که در زیر منحنی $$|x|$$ قرار دارند، زیردیفرانسیل این تابع خواهند بود.

به عنوان یک مثال دیگر به تابعی که در تصویر 4 دیده می‌شود، توجه کنید. این تابع در یک یا چند نقطه از دامنه‌اش، دارای شکست است. فرض کنید می‌خواهیم زیردیفرانسیل این تابع را در نقطه $$x_0$$ مشخص کنیم. در این تصویر، تابع محدب به رنگ آبی مشخص شده و خطوط قرمز رنگ، زیرمشتق‌های آن را در نقطه $$x_0$$ نشان می‌دهند.

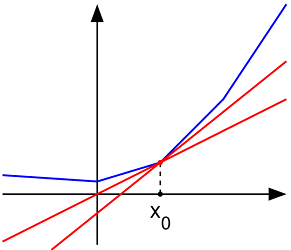
واضح است که شیب همه خطوط مماس بر تابع در نقطه $$x_0$$، پاسخ‌های زیردیفرانسیل تابع $$f(x)$$ در نقطه $$x_0$$ با توجه به شرط مربوط به رابطه ۳ خواهند بود.

نکته: همانطور که متوجه شدید، زیرمشتق، یک مجموعه است که توسط رابطه ۱ مشخص شده است. به این ترتیب مجموعه نقاط زیرمشتق تابع $$f$$، به نقاطی از دامنه تابع (مثل $$c$$) گفته می‌شوند که در رابطه ۳ صدق می‌کنند. اگر این مجموعه، شامل فقط یک نقطه باشد، زیرمشتق‌ها تبدیل به مشتق شده و تابع را مشتق‌پذیر می‌نامند.

خصوصیات زیرمشتق تابع

همانطور که مشتق و مشتق‌پذیری توابع دارای خصوصیات بودند، برای زیرمشتق تابع نیز می‌توان ویژگی‌های زیر را اثبات کرد.

• تابع محدب $$f$$ روی اعداد حقیقی، مشتق‌پذیر در $$x_0$$ است، اگر و فقط اگر نقاط زیرمشتق آن فقط یک نقطه باشد. به بیان دیگر مجموعه زیرمشتق‌های آن فقط شامل یک نقطه بوده که همان مشتق تابع در نقطه $$x_0$$ است.
• نقطه $$x_0$$ یک نقطه کمینه فراگیر برای تابع محدب $$f$$ است، اگر و فقط اگر صفر در مجموعه زیرمشتق‌های تابع، وجود داشته باشد. به این معنی که بتوان خطوط افقی (به نام خط زیرمشتق) روی نمودار تابع $$f$$ از نقطه $$\Big(x_0,f(x_0)\Big)$$ ترسیم کرد. همانطور که مشخص است این خاصیت، همان وجود مقدار کمینه محلی برای تابع مشتق‌پذیر است.
• اگر تابع $$f$$ و $$g$$ محدب بوده و زیرمشتق‌های $$\partial f(x)$$ و $$\partial g(x)$$ موجود باشند، آنگاه برای مجموع این دو تابع هم داریم:

$$\partial ( f + g )(x) = \partial f(x) + \partial g(x)$$

نکته: منظور از رابطه + در فرمول بالا، «جمع مینکوفسکی» (Minkowski Sum) است. زیرا که $$\partial f(x)$$ و $$\partial g(x)$$ هر دو یک مجموعه هستند. توجه داشته باشید که جمع مینکوفسکی دو مجموعه $$A$$ و $$B$$ به صورت زیر تعریف شده است.

$$\large A + B = \{ \mathbf {a} + \mathbf {b} \, | \, \mathbf {a} \in A ,\ \mathbf {b} \in B \}$$

رابطه 4

زیرگرادیان

همانطور که دیدید، مفهوم مشتق را می‌توان به زیرمشتق برای یک تابع محدب گسترش داد. در این بین مفهوم گرادیان (مشتق جهت دار) به زیرگرادیان (Subgradient) قابل توسعه است. به این ترتیب براساس یک تابع چند متغیره می‌توان زیرمشتق را تعریف و به کار گرفت.

فیلم آموزش کاربرد مشتق در ریاضیات (برای مدیریت، حسابداری و اقتصاد) (رایگان) در فرادرس

کلیک کنید

فرض کنید تابع $$f$$ یک تابع حقیقی مقدار محدب باشد که روی یک مجموعه محدب باز (Convex open set) در فضای اقلیدسی $$R^n$$ تعریف شده است.

$$\large f : U \to R$$

بردار $$\overrightarrow{\nu}$$ در این فضا را یک زیرگرادیان در نقطه $$\overrightarrow{x_0}$$ در $$U$$ برای تابع $$f$$ گویند اگر برای هر $$\overrightarrow{x}$$ در $$U$$ رابطه 5 برقرار باشد.

$$\large f(\overrightarrow{x}) - f(\overrightarrow{x_0}) \geq \overrightarrow{\nu} \cdot (\overrightarrow{x} - \overrightarrow{x_{0}})$$

رابطه ۵

نکته: در این جا منظور از $$\overrightarrow{\nu} \cdot (\overrightarrow{x} -\overrightarrow{x_{0}} )$$ ضرب داخلی (Dot Product) دو بردار $$\overrightarrow{\nu}$$ و $$\overrightarrow{x} -  \overrightarrow{x_0}$$ است.

مجموعه همه گرادیان‌های نقطه $$x_0$$ را زیردیفرانسیل در نقطه $$x_0$$ نامیده و به صورت $$\partial f(x_0)$$ نشان می‌دهند. به این موضوع توجه داشته باشید که زیردیفرانسیل همیشه یک «مجموعه ناتهی محدب فشرده» (Nonempty Convex Compact Set) است.

همین مفهوم را به تابع محدب و «فضای محدب محلی» (Locally Convex Space) مثل $$V$$ توسعه می‌دهیم. فرض کنید که تابع $$f$$ یک تابع چند متغیره روی $$V$$ است. به این معنی که داریم:

$$\large f : U \to \mathbf{R}$$

تابعک (Functional) $$v^*$$ در فضای مضاعف $$V^*$$ (Dual Space) را یک زیرگرادیان $$x_0$$ در $$U$$ گویند اگر برای هر $$x$$ در $$U$$ داشته باشیم:

$$\large f(x) - f(x_{0}) \geq v^{*}(x - x_{0})$$

رابطه ۶

مجموعه همه زیرگرادیان‌های $$x_0$$ که در رابطه ۶ صدق کنند، زیردیفرانسیل تابعک (Functional) $$v^*$$ در $$x_0$$ گفته و به صورت $$\partial f ( x_0 )$$ نشان می‌دهند.

خلاصه و جمع‌بندی

در این نوشتار به تعمیم موضوع مشتق پرداخته و با زیرمشتق به عنوان یک زیر مجموعه از مقادیر دامنه تابع آشنا شدیم. همچنین رابطه‌ای که مقادیر زیرمشتق یک تابع محدب را مشخص می‌کند در این نوشتار معرفی شده و با استفاده از تابع قدر مطلق مفهوم زیرمشتق بیشتر روشن گردید. علاوه بر زیرمشتق، مفاهیم دیگر مانند زیرگرادیان و زیردیفرانسیل نیز از مواردی است که در این نوشتار به آن پرداخته شد.

این مفاهیم بخصوص برای حل مسائل بهینه‌سازی چند متغیره در مهندسی و رشته‌های صنایع به کار گرفته می‌شود. از آنجایی که بسیاری از تبدیلات در ریاضیات براساس توابع محدب انجام می‌شوند، وجود زیرمشتق برای آن‌ها در علوم و فنونی که از این گونه تبدیلات استفاده می‌کنند، امری مهم تلقی می‌شود.