راکتانس القایی — به زبان ساده

در آموزش‌های قبلی مجله فرادرس، با اتصال سری و اتصال موازی سلف‌ها آشنا شدیم. در این آموزش، در مورد مفهوم راکتانس القایی بحث خواهیم کرد. رفتار جریان گذرنده از یک سلف، زمانی که یک ولتاژ متناوب (AC) یا یک ولتاژ مستقیم (DC) به دو سر آن اعمال شود، بسیار متفاوت است. منبع تغذیه سینوسی باعث به وجود آمدن اختلاف فاز بین شکل موج جریان و ولتاژ می‌شود. زمانی که یک جریان متناوب از مدار عبور می‌کند، مخالفت در برابر جریان گذرنده از سیم‌پیچ‌ها نه تنها به مقدار اندوکتانس سیم‌پیچ وابسته است، بلکه فرکانس شکل موج AC نیز در آن تاثیرگذار خواهد بود.

راکتانس القایی

میزان مخالفت با جریان گذرنده از یک سیم‌پیچ در یک مدار AC، توسط مقاومت AC تعیین می‌شود. این مقاومت را معمولا با نام «امپدانس» (Impedance) یا Z می‌شناسند.

فیلم آموزش ماشین های الکتریکی 3 در فرادرس

کلیک کنید

مشابه مقاومت، واحد راکتانس نیز «اهم» (Ohm) است. با این تفاوت که برای تشخیص راحت‌تر آن از مقدار مقاومت خالص (R)، از نماد X‌ استفاده می‌شود. از آنجایی که این مقدار مقاومت مربوط به المان سلف است، راکتانس سلف را «راکتانس القایی» (Inductive Reactance) می‌گویند. به عبارت دیگر، زمانی که یک سلف در یک مدار AC به کار می‌رود، مقاومت الکتریکی آن، راکتانس القایی نامیده می‌شود.

راکتانس القایی با $$X_L$$‌ نشان داده می‌شود و نشان دهنده مخالف با تغییر جریان در یک مدار AC‌ است. در یک مدار AC سلفی خالص، مخالفت کامل زمانی رخ می‌دهد که جریان $$I_L$$ نسبت به ولتاژ مدار «پس‌فاز» (Lag) باشد؛ به عبارت دیگر، اختلاف فاز بین جریان و ولتاژ، برابر با $$90^{\circ}$$ یا ($$\pi/2\,\,\text rads$$) باشد.

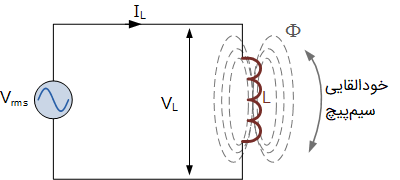
در مدار سلفی خالص بالا، سیم‌پیچ مستقیما به منبع ولتاژ AC‌ متصل است. اگر فرکانس منبع ولتاژ افزایش یا کاهش یابد، با توجه به این تغییرات، نیرو محرکه الکتریکی معکوسِ القا شده توسط خود سلف (Self-induced Back emf) نیز افزایش یا کاهش پیدا می‌کند.

می‌دانیم که این نیرو محرکه الکتریکی القایی با تغییرات جریان گذرنده از سیم‌پیچ متناسب است. در شکل زیر مشاهده می‌شود که این جریان در $$180^\circ$$ ماکزیمم است. در این نقطه، ولتاژ و نیرو محرکه الکتریکی القا شده صفر هستند.

همچنین، مشاهده می‌شود که در زمان ماکزیمم و مینیمم ولتاژ ($$90^{o}\,,\,270^{o}$$)، جریان برابر با صفر است.

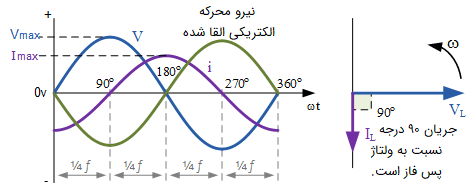
از شکل موج جریان و ولتاژ بالا متوجه می‌شویم زمانی که جریان نسبت به ولتاژ $$90^{\circ}$$ پس‌فاز باشد، مدار سلفی خالص است. به همین ترتیب، هنگامی که ولتاژ نسبت به جریان $$90^{\circ}$$ پیش‌فاز باشد نیز مدار سلفی است. اما باید دقت کرد که مشابه شکل بالا، پس‌فاز بودن جریان نسبت به ولتاژ، یک بیان استاندارد است. در اینجا، جریان و ولتاژ اختلاف فاز $$90^{\circ}$$ دارند و جریان نسبت به ولتاژ پس‌فاز است.

همچنین، اگر ولتاژ را به عنوان مبدا در نظر بگیریم، می‌توانیم این عبارت را به دو صورت $$V_L=0^{\circ}$$ و $$I_L=-90^{\circ}$$‌ بیان کنیم. به عبارت دیگر، اگر ولتاژ را به عنوان یک موج سینوسی در نظر بگیریم، در این صورت جریان یک شکل موج کسینوسی منفی خواهد بود. در این حالت، مقدار جریان گذرنده از مدار در هر لحظه به صورت زیر است:

$$\large I_L=I_{max}\,\sin(\omega t-90^{0})$$

که در آن، $$\omega$$ بر حسب رادیان بر ثانیه و t بر حسب ثانیه است.

از آنجایی که در مدارهای سلفی خالص، جریان همیشه $$90^{0}$$ نسبت به ولتاژ پس‌فاز است، با داشتن فاز ولتاژ می‌توان فاز جریان را نیز به دست آورد و بالعکس. با داشتن فاز جریان در مدار سلفی خالص، می‌توان فاز ولتاژ را به راحتی محاسبه کرد. بنابراین، اگر $$V_L$$ را داشته باشیم، $$I_L$$ باید $$90^{\circ}$$ پس فاز باشد. به همین ترتیبت، اگر $$I_L$$ مشخص باشد، $$V_L$$ را با $$90^{\circ}$$ پیش‌فاز به دست می‌آوریم. پس، با تقسیم مقدار ولتاژ به جریان، راکتانس القایی ($$X_L$$) سیم‌پیچ به دست می‌آید:

$$\large X_L=\frac{V_L}{I_L}=\omega L\,\,(\Omega)$$

می‌توانیم فرمول بالا را به شکل محبوب‌تر و بر اساس راکتانس القایی بنویسیم. در این حالت، راکتانس القایی به جای فرکانس زاویه‌ای ($$\omega$$)، بر اساس فرکانس معمولی است. این فرمول در زیر نشان داده شده است:

$$\large X_L=2\pi fL$$

که در آن، $$f$$ فرکانس، $$L$$ اندوکتانس سیم‌پیچ و $$2\pi f=\omega$$ است.

از معادله بالا برای راکتانس القایی مشاهده می‌شود که اگر فرکانس یا اندوکتانس افزایش یابد، مقدار راکتانس القایی نیز زیاد خواهد شد. به همین ترتیب، اگر فرکانس بینهایت باشد، مقدار راکتانس القایی نیز به بینهایت می‌رسد. در این حالت، سلف مانند یک مدار باز عمل خواهد کرد.

بنابراین اگر فرکانس صفر شود (مدار DC باشد)، مقدار راکتانس القایی نیز صفر خواهد بود. در این حالت، سلف مانند یک اتصال کوتاه عمل می‌کند. پس نتیجه می‌گیریم که راکتانس القایی، متناسب با مقدار فرکانس مدار است.

به عبارت دیگر، با افزایس فرکانس، راکتانس القایی ($$X_L$$) نیز زیاد می‌شود و با کاهش آن، راکتانس القایی کاهش می‌یابد. رابطه بین فرکانس و راکتانس القایی در شکل زیر نشان داده شده است.

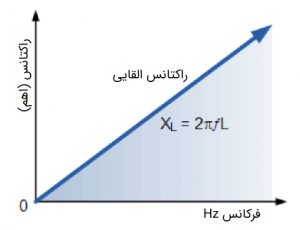
در شکل بالا، شیب نمودار نشان دهنده رابطه مستقیم بین راکتانس القایی و فرکانس منبع است. بنابراین، راکتانس القایی متناسب با فرکانس است ($$X_L\,\propto\,f$$).

مثال ۱

یک سیم‌پیچ با راکتانس 150mH و مقاومت صفر به یک منبع با ولتاژ 100V و فرکانس 50Hz‌ متصل است. راکتانس القایی سیم‌پیچ و جریان گذرنده از آن را محاسبه کنید.

حل:

$$\large X_L=2\pi fL=2\pi \times50\times0.15=47.12\,\, \Omega$$

$$\large I=\frac{V}{X_L}=\frac{100}{47.12}=2.12\,\,A$$

مدار RL با تغذیه AC

تا اینجا سلف را ایده‌آل درنظر گرفتیم. به عبارت دیگر، فرض کردیم سیم‌پیچ، القایی خالص است. اما می‌دانیم که ساخت سیم‌پیچ با اندوکتانس خالص عملا غیرممکن است. سیم‌پیچ‌ها، هرچقدر هم که کوچک باشند، مقدار مشخصی مقاومت دارند. بنابراین، یک سیم‌پیچ (سلف) را معمولا با یک اندوکتانس و یک مقاومت معادل‌سازی می‌کنند.

فیلم آموزش مدارهای الکتریکی 1 – مرور و حل تست در فرادرس

کلیک کنید

در یک مدار با منبع AC که با اندوکتانس (L) و مقاومت (R) سری شده است، مقدار فازور ولتاژ برابر با مولفه ولتاژ راکتانس ($$V_L$$) و مولفه ولتاژ مقاومت ($$V_R$$) است. این یعنی جریان گذرنده از سیم‌پیچ همچنان نسبت به ولتاژ پس‌فاز است، اما با توجه به مقدار $$V_L$$ و $$V_R$$، مقدار آن از $$90^{\circ}$$ کمتر خواهد بود.

مقدار فاز جدید بین ولتاژ و جریان، به عنوان زاویه فاز مدار شناخته می‌شود و نماد یونانی $$\phi$$ برای آن به کار می‌رود.

برای نوشتن رابطه برداری بین ولتاژ و جریان، باید یک مولفه یکسان به عنوان مرجع در نظر گرفته شود. در یک مدار با اتصال سری سلف و مقاومت، مولفه‌ جریان از هر دو المان (سلف و مقاومت) عبور خواهد کرد. بردار مرجع به صورت یک خط افقی از چپ به راست کشیده می‌شود.

از آموزش مقاومت و خازن می‌دانیم که جریان و ولتاژ در یک مدار AC مقاومتی «همفاز» (In-phase) هستند. بنابراین، بردار $$V_R$$ روی بردار $$V_I$$ رسم می‌شود. 

همچنین، همانطور که پیش‌تر نیز گفته شد، در یک مدار سلفی خالص، جریان $$90^{\circ}$$ نسبت به ولتاژ پس‌فاز است. بنابراین، بردار  $$V_L$$ به اندازه $$90^{\circ}$$  جلوتر از بردار جریان رسم می‌شود و البته هم‌فاز با بردار $$V_R$$ است. این موضوع را در شکل زیر مشاهده می‌کنید.

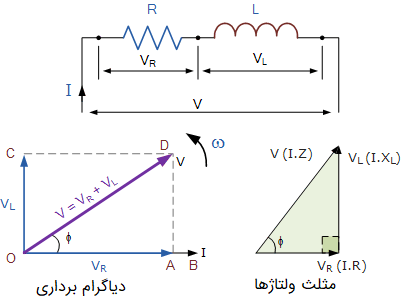
در نمودار بالا مشاهده می‌شود که خط OB نشان‌ دهنده خط مرجع جریان و خط OA نشان‌ دهنده ولتاژ مقاومت است که این دو هم‌راستا (همفاز) هستند. خط OC ولتاژ اندوکتانس را نشان می‌دهد که $$90^{\circ}$$ جلوتر از جریان است. این حالت به این معناست که جریان $$90^{\circ}$$ نسبت به ولتاژ پس‌فاز است. خط OD مجموع ولتاژ دو مولفه مقاومت و سلف مدار است. مثلث ولتاژ نیز از معادله فیثاغورس به دست آمده که به صورت زیر است:

$$\large V^{2}=V_R^2+V_L^2$$

$$\large V=\sqrt{V_R^2+V_L^2}$$

$$\;\;\;\large \tan(\phi)=\frac{V_L}{V_R}$$

$$\;\;\;\;\large V_R=I\times R\;\;\;\;\;,\;\;\;\;\;V_L=I\times X_L$$

$$\large V=\sqrt{(I\times R)^2\,+\,(I \times X_L)^2}$$

$$\\;\;\large I=\frac{V}{R^2\;+\;X_L^2}=\frac{V}{Z}\;\;(A)$$

در یک مدار DC، نسبت ولتاژ به جریان را مقاومت می‌گویند. بنابراین، در مدار AC، این نسبت ام‍پدانس (Z) نامیده می‌شود. واحد امپدانس نیز اهم (Ohm) است. در واقع امپدانس، کل مقاومتی است که مجموعه مقاومت و راکتانس القایی در مقابل جریان از خود نشان می‌دهند.

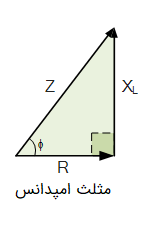
اگر دو طرف مثلث ولتاژ بالا را بر جریان تقسیم کنیم، مثلت دیگری تولید می‌شود که نشان‌ دهنده رابطه فیثاغورس مقاومت‌، راکتانس و امپدانس است. این مثلث جدید با نام «مثلث امپدانس» (Impedance Triangle) شناخته می‌شود و در شکل زیر نمایش داده شده است.

$$\large Z=\sqrt{R^2\;+\;X_L^2}$$

$$\large \tan(\phi)=\frac{X_L}{R}$$

$$\large \sin(\phi)=\frac{X_L}{Z}$$

$$\large \cos(\phi)=\frac{R}{Z}$$

مثال ۲

یک سیم‌پیچ سلونوئیدی، مقاومتی برابر با $$30$$ اهم و اندوکتانسی برابر با $$0.5\, \text{H}$$ دارد. همچنین، جریان گذرنده از سیم‌پیچ $$4$$ آمپر است.

الف) اگر فرکانس $$50$$ هرتز باشد، ولتاژ منبع را محاسبه کنید.

$$\large X_L=2\pi fL$$

$$\large X_L=2\pi\,\, 50\times 0.5$$

$$\large X_L=157\,\, \Omega$$

$$\large Z=\sqrt{R^2\,\,+X_L^2}$$

$$\large Z=\sqrt{30^2\,\,+157^2}$$

$$\large Z=160\,\,\Omega$$

$$\large V=I\times Z=4\times160=640\,V$$

ب) زاویه فاز بین ولتاژ و جریان را به دست آورید.

$$\large tan\,\phi =\frac{X_L}{R}$$

$$\therefore\;\;\;\large \phi =tan^{-1}\frac{X_L}{R}=\frac{157}{30}=79.2^0\;\;\;lagging$$

مثلث توان یک سلف AC

یکی دیگر از ساختارهای مثلثی که برای مدار سلفی به کار می‌رود، «مثلث توان» (Power Triangle) است. توان در مدار سلفی با عنوان‌هایی مانند «توان راکتیو» (Reactive Power) و «ولت آمپر راکتیو» (Volt-amps Reactive) به کار می‌رود. این توان با Var نشان داده می‌شود و بر حسب ولت آم‍پر است. در یک مدار سلفی-مقاومتی AC، جریان نسبت به ولتاژ به اندازه $$\phi^{\circ}$$ پس‌فاز است.

فیلم آموزش ماشین های سنکرون (رایگان) در فرادرس

کلیک کنید

در یک مدار سلفی خالص AC، جریان دقیقا به اندازه $$90^{\circ}$$ نسبت به ولتاژ اختلاف فاز دارد. توان راکتیو کل سلف برابر با صفر است؛ به این دلیل که تمام توان آن، توسط نیرو محرکه الکتریکی القا شده در خودش مصرف می‌شود. به عبارت دیگر، توان خالص بر حسب وات (Watt) در طول یک دوره کامل، تماما توسط سلف مصرف می‌شود. همچنین، تمام انرژی راکتیو تولید شده توسط منبع مدار، دوباره به خودش برمی‌گردد.

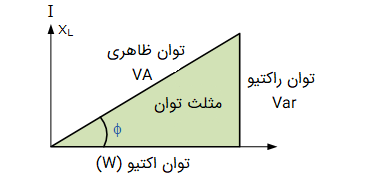
توان راکتیو (Q) یک سلف برابر با $$I^2\times X_L$$ است (مشابه $$I^2\times R$$ در یک مدار DC). بنابراین، سه ضلع مثلث توان در یک مدار AC با «توان ظاهری» (Apparent Power) یا S، «توان اکتیو» (Real Power) یا P و «توان راکتیو» (Reactive Power) یا Q نشان داده می‌شود.

$$\large P=VI\,cos\,\phi\;\;\;\;\;\;\;\;S=VI\;\;\;\;\;\;\;Q=VI\,sin\,\phi$$

$$\large VA=\sqrt{P^2+{Var}^2}$$

اگر این آموزش برای شما مفید بوده و می‌خواهید درباره مباحث مربوط به آن، بیشتر بدانید، آموزش‌های زیر را به شما پیشنهاد می‌کنیم:

• مجموعه آموزش‌های مهندسی برق
• آموزش مدارهای الکتریکی ۱
• مجموعه آموزش‌های مهندسی قدرت
• آموزش مبانی مهندسی برق ۱
• القای الکترومغناطیسی (Electromagnetic Induction) — از صفر تا صد
• دوقطبی در مدارهای الکتریکی — به زبان ساده
• مدار مرتبه اول RL — از صفر تا صد

^^